Comparing Automatic Modeling Procedures of TRAMO and X-12

Comparing Automatic Modeling Procedures of TRAMO and X-12 -ARIMA, an Update Kathy Mc. Donald-Johnson, U. S. Census Bureau Catherine Hood, Catherine Hood Consulting Brian Monsell, U. S. Census Bureau Chak Li, U. S. Census Bureau ICES III June 2007

Acknowledgments • Agustín Maravall • Víctor Gómez • Rita Petroni • James Gomish 2

Update • Similar comparisons in the past, especially Farooque, Hood, and Findley (2001) » X-12 -ARIMA chose models of similar quality to TRAMO models » X-12 -ARIMA perhaps better at identifying trading day effects than TRAMO 3

Update, Similar Approach • We used a similar approach to that of Farooque, Hood, and Findley (2001), but we used improved versions of both programs 4

Outline • Background on Automatic Modeling • Methods • Results » Actual time series » Simulated time series • Conclusions 5

Background

Automatic ARIMA Modeling • X-11 -ARIMA from Statistics Canada, Dagum » Picks best model from list • TRAMO (Time series Regression with ARIMA noise, Missing observations and Outliers) from the Bank of Spain, Gómez and Maravall » Multiple steps to obtain a model 9

TRAMO Automatic Modeling • Gómez and Maravall (2000) gives • description FORTRAN code from Gómez and Maravall provides additional detail » Generously provided to U. S. Census Bureau for X-12 -ARIMA Version 0. 3 development 10

X-12 -ARIMA Version 0. 3 • Retains pick model method » Pickmdl specification • Adds step-through method based on the TRAMO method » Automdl specification 11

X-12 -ARIMA Comparisons • Dent, Hood, Mc. Donald-Johnson, and Feldpausch (2005) compared the stepthrough method to the pick model method » Models of similar quality » Step-through method more flexible 12

X-12 -ARIMA's Automatic Transformation Selection • Identification with the transform specification • Fit a default model with the log transformation and with no transformation » Usually the airline model (0 1 1) from Box and Jenkins (1976) • The model is chosen whose maximum likelihood value is larger » Likelihood of the log data is adjusted to be a likelihood of the untransformed data 13

• By default, slight bias toward the log transformation 14

X-12 -ARIMA's Automatic Regression Selection • Trend Constant » Identification with the step-through method, automdl specification • Outliers » Identification with the outlier specification 15

X-12 -ARIMA's Automatic Regression Selection Trading-Day Effect Easter Effect • Identification with the regression specification, aictest argument • Test uses the AICC » No bias (user can set bias) 16

AICC • AIC Corrected (for sample size) • Note: As N gets larger, AICC approaches the AIC 17

Trading-Day Effects • User specifies type » Flow (cumulative) » Stock (inventory) • X-12 -ARIMA compares AICC with and without the effect » No bias (user can set bias) 18

Easter Effects • Default tests for Easter effects of length 1, 8, and 15 days » User can specify length • X-12 -ARIMA compares four AICC values » No effect vs. each of the three different length effects » No bias (user can set bias) 19

Modeling Diagnostics • Ljung-Box Q » Goodness-of-fit diagnostics (Ljung and Box 1978) • Spectrum of the model residuals » Diagnostic indicating seasonal or trading day effects remaining in the model residuals Trading day frequencies defined in Cleveland Devlin (1980) » 20

Ljung-Box Q • Based on sample autocorrelation of the • • • reg. ARIMA model residuals Residuals should behave like white noise Each Ljung-Box Q statistic of positive degrees of freedom has a corresponding p value An individual lag fails if the p value for the Q statistic for the lag is less than 0. 05 21

Ljung-Box Q Failure For this study If seven or more of the first 12 lags fail or If 13 or more of the first 24 lags fail or If lag 12 fails • • • Then the model fails according to this diagnostic 22

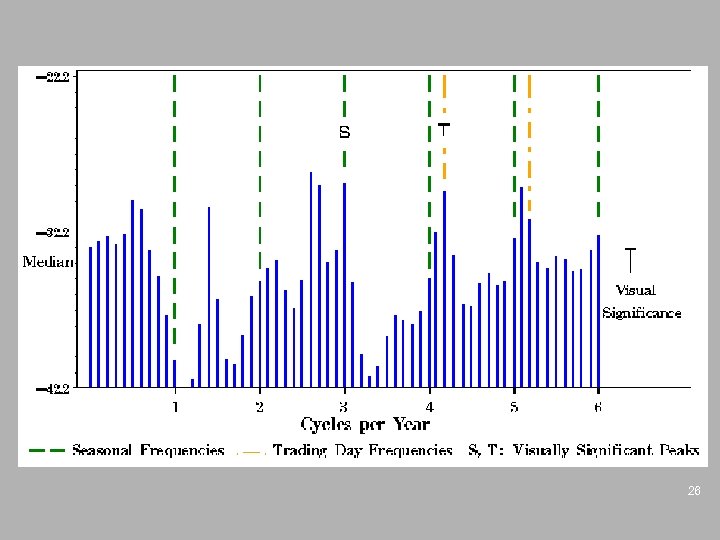
Spectrum of the Model Residuals • Diagnostic indicating strength at • frequencies of interest Visually significant peaks at seasonal or trading day frequencies indicate possible model problems 23

Significant Spectrum Peaks • A spectral peak is considered to be significant if it » Reaches a height beyond the median height of all the frequency measures » Are taller than nearest neighbors by a visually significant amount 24

Significant Spectrum Peaks For this study, any significant peak at » seasonal frequencies one, two, three, for or five cycles per year and » At either of the two trading-day frequencies indicates model failure according to this diagnostic 25

26

Spectrum Diagnostic Information • Graphical form » Output file line printer graph » Higher resolution graph • Text form » Log file » Diagnostics file • Failure warnings listed onscreen when X 12 -ARIMA runs 27

Methods

Automatic Modeling Settings • Test for log transformation • Automatic reg. ARIMA model identification • Automatic outlier detection • Test for » Usual trading day » Leap year » Easter effects 29

Settings for X-12 -ARIMA • We expected some quarterly effects (higher autocorrelation three months apart), so we chose the maximum nonseasonal model order (maximum p, q) to be three » Default is two • We chose to prefer balanced models to have an approach more like the TRAMO procedure » Default is not to prefer balanced models 30

Model Choices • Ran TRAMO, X-12 -ARIMA to identify transformation, model • Hard-coded results into X-12 -ARIMA input specification files • Compared diagnostics from X-12 -ARIMA 31

Clarification • "TRAMO model" results are from X 12 -ARIMA runs » Initial TRAMO runs determined the transformation and model choices 32

Changes to Models • Used X-12 -ARIMA outlier set • If any Easter regressor chosen, used X 12 -ARIMA Easter effect of eight days 33

Actual Time Series

457 U. S. Census Bureau Series • U. S. Building Permits • Manufacturing • Retail Sales • Import/Export data Descriptions available at www. census. gov/cgi-bin/briefroom/Brief. Rm 35

Transformation Choice • TRAMO and X-12 -ARIMA agreed for 91% (417) of the series • 40 series differed » 85% (34/40) TRAMO chose log and X-12 ARIMA chose no transformation » 15% (6/40) X-12 -ARIMA chose log and TRAMO chose no transformation 36

Transformation Choice • Transformation choice is fundamental • We did not want to favor one program’s • transformation over the other We dropped the 40 series of disagreement from further comparisons 37

Full Model Agreement (of 417 Series) • 30% (124) of the reg. ARIMA models agreed » Any length Easter considered match • 293 series to compare diagnostics 38

ARIMA Model Agreement (of 293 Series) • 24% (70) of the ARIMA models agreed, showing differences only in the chosen regression effects 39

Easter Effects • 76% (222) Easter effect agreement » 13% (37) both programs chose an Easter effect » 63% (185) neither program chose an Easter effect • 24% (71) Easter effect disagreement » 24% (70) X-12 -ARIMA chose Easter and TRAMO did not » 0. 3% (1) TRAMO chose Easter and X-12 -ARIMA did not 40

Why Does X-12 -ARIMA Include Easter Effects More Often? • TRAMO checks for an Easter effect of • one length X-12 -ARIMA checks for three different lengths • Do more possible regressors raise the chance of including an Easter effect? 41

Are the Easter Effects Appropriate? • These economic series could indeed have Easter effects, but the results for X-12 -ARIMA show Easter effects to be more prevalent than we would have expected 42

Trading-day Effects • 57% (166) trading day agreement » 24% (70) both programs chose trading-day effects » 33% (96) neither program chose trading-day effects • 43% (127) trading day disagreement » 35% (104) X-12 -ARIMA chose trading-day effects and TRAMO did not » 8% (23) TRAMO chose trading-day effects and X 12 -ARIMA did not 43

Appropriate Trading-day Effects • Under specific conditions, we can evaluate whether a trading-day effect was missed » One model includes a trading-day effect but the other does not » The model with a trading-day effect has no spectrum peak at either trading-day frequency, but the model without a trading-day effect results in a peak at one or both of the trading-day frequencies 44

Trading Day Omitted • 22% (64) of the series had this omission problem » 20% (60) TRAMO omission » 1% (4) X-12 -ARIMA omission • Using a binomial distribution, the probability of seeing 60 out of 64 failures for one method if the probability of failure were equally 0. 5 for each method is less than 0. 01 45

Ljung-Box Q Model Failures • 24% (69) one model passed and the other model failed » 17% (50) TRAMO model failed » 6% (19) X-12 -ARIMA model failed • Binomial probability that 50 of 69 failures would be from one method is less than 0. 01 47

Seasonal Spectrum Model Failures • 14% (41) one model passed and the other model failed » 8% (24) TRAMO model failed » 6% (17) X-12 -ARIMA model failed • Binomial probability of 24 of 41 failures being from one method is not significant at the 10% level, so there was no significant difference in the seasonal spectrum results 48

Simulated Time Series

Airline Model Series (0 1 1) • 3, 500 monthly series • 15 years long • Nonseasonal moving average • • coefficient 0. 6 Seasonal moving average coefficient 0. 9 Start date 1980 (arbitrary choice) 51

No Model • 0. 6% (21) X-12 -ARIMA did not choose a model • TRAMO identified a model for each series 52

Fully Correct Model Identification • Airline model with no trading day or Easter effects • 66% (2, 305) TRAMO correct • 72% (2, 516) X-12 -ARIMA correct 53

Correct ARIMA Identification • Also identified trading day or Easter effects • 85% (2, 978) TRAMO correct ARIMA • 90% (3, 159) X-12 -ARIMA correct ARIMA 54

Nonseasonal Differencing • 99% (3, 480) TRAMO chose • nonseasonal difference of order 1 99% (3, 466) X-12 -ARIMA chose nonseasonal difference of order 1 55

Seasonal Differencing • 97% (3, 378) TRAMO chose seasonal • differencing of order 1 99% (3, 470) X-12 -ARIMA chose seasonal differencing of order 1 56

Easter Effect Identification • 4% (148) TRAMO chose Easter effect • 11% (392) X-12 -ARIMA chose Easter effect • No Easter effect present • Binomial probability is less than 0. 01 that we would see such a difference assuming equal probabilities of selection 57

Trading-day Effect Identification • 13% (460) TRAMO chose trading-day effect • 4% (138) X-12 -ARIMA chose trading-day effect • Binomial probability is less than 0. 01 that we would see such a difference assuming equal probabilities of selection 58

Conclusions • X-12 -ARIMA mistakenly chooses an • Easter effect more often than TRAMO As noted in Farooque, Hood, and Findley (2001), X-12 -ARIMA still seems to choose trading-day effects more appropriately than TRAMO 59

Conclusions • For known airline model simulations, X • 12 -ARIMA performed as well as TRAMO in identifying the ARIMA model X-12 -ARIMA models performed as well as TRAMO when measured by the standard model diagnostics » Ljung-Box Q » Spectrum of the model residuals 60

Newer Version of X-12 -ARIMA • We now have an improved version of X- 12 -ARIMA and hope to rerun the model identification to see if there any changes to these results 61

Future Work • Expand the study of simulated series to • perform a more thorough evaluation of X 12 -ARIMA’s new automatic modeling procedure using more varied models, model coefficients, regression effects, and series lengths Investigate how to improve the selection of the Easter effect 62

Disclaimer This report is released to inform interested parties of ongoing research and to encourage discussion of work in progress. Any views expressed on statistical, methodological, technical, or operational issues are those of the authors and not necessarily those of the U. S. Census Bureau. 63

Much of the data analysis for this paper was generated using Base SAS® software, SAS/AF® software, and SAS/GRAPH® software, Versions 8 and 9 of the SAS System for Windows. Copyright © 19992003 SAS Institute Inc. SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. , Cary, NC, USA. 64

We used R to simulate the airline model time series. Additional analysis was performed using Microsoft® Excel 2000. Copyright © 1985 -1999 Microsoft Corporation. We checked our own calculations of the binomial probabilities involving the actual data using the Binomial Calculator at onlinestatbook. com/java/binomial. Prob. html (home page at onlinestatbook. com), and we used it alone for the comparisons involving the simulated data. 65

66