611baef201b3236bf918dbf477623137.ppt
- Количество слайдов: 56

COMP 5331 Classification Prepared by Raymond Wong The examples used in Decision Tree are borrowed from LW Chan’s notes Presented by Raymond Wong raywong@cse COMP 5331 1
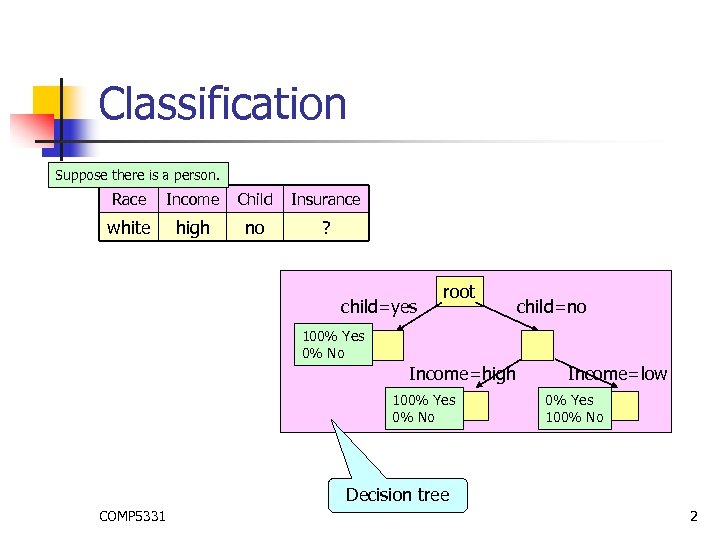
Classification Suppose there is a person. Race Income Child Insurance white high no ? child=yes root child=no 100% Yes 0% No Income=high 100% Yes 0% No Income=low 0% Yes 100% No Decision tree COMP 5331 2
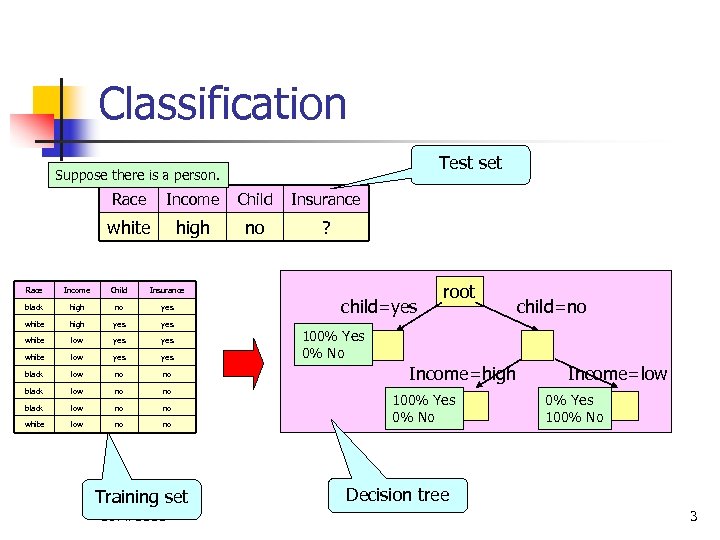
Classification Test set Suppose there is a person. Race Income Child Insurance white high no ? Race Income Child Insurance black high no yes white high yes yes white low yes black low no no white low no no Training set COMP 5331 child=yes root child=no 100% Yes 0% No Income=high 100% Yes 0% No Income=low 0% Yes 100% No Decision tree 3

Applications n Insurance n According to the attributes of customers, n n Marketing n According to the attributes of customers, n n Determine which customers will buy an insurance policy Determine which customers will buy a product such as computers Bank Loan n According to the attributes of customers, n COMP 5331 Determine which customers are “risky” customers or “safe” customers 4

Applications n Network n According to the traffic patterns, n n Determine whether the patterns are related to some “security attacks” Software n According to the experience of programmers, n COMP 5331 Determine which programmers can fix some certain bugs 5

Same/Difference n n Classification Clustering COMP 5331 6

Classification Methods n n n Decision Tree Bayesian Classifier Nearest Neighbor Classifier COMP 5331 7
Decision Trees n n n ID 3 C 4. 5 CART COMP 5331 Iterative Dichotomiser Classification And Regression Trees 8

Entropy n Example 1 n n n Consider a random variable which has a uniform distribution over 32 outcomes To identify an outcome, we need a label that takes 32 different values. Thus, 5 bit strings suffice as labels COMP 5331 9

Entropy n n n Entropy is used to measure how informative is a node. If we are given a probability distribution P = (p 1, p 2, …, pn) then the Information conveyed by this distribution, also called the Entropy of P, is: I(P) = - (p 1 x log p 1 + p 2 x log p 2 + …+ pn x log pn) All logarithms here are in base 2. COMP 5331 10

Entropy n For example, n n n If P is (0. 5, 0. 5), then I(P) is 1. If P is (0. 67, 0. 33), then I(P) is 0. 92, If P is (1, 0), then I(P) is 0. The entropy is a way to measure the amount of information. The smaller the entropy, the more informative we have. COMP 5331 11

Race Info(Tblack) = - ¾ log ¾ - ¼ log ¼ = 0. 8113 high no yes white high yes white low yes yes black low no no black For attribute Race, Insurance white Info(T) = - ½ log ½ =1 Child black Entropy Income low no no white low no no Info(Twhite) = - ¾ log ¾ - ¼ log ¼ = 0. 8113 Info(Race, T) = ½ x Info(Tblack) + ½ x Info(Twhite) = 0. 8113 Gain(Race, T) = Info(T) – Info(Race, T) = 1 – 0. 8113 = 0. 1887 For attribute Race, COMP 5331 Gain(Race, T) = 0. 1887 12

Race yes high yes yes low yes black low no no black Info(Tlow) = - 1/3 log 1/3 – 2/3 log 2/3 no white low no no white Info(Thigh) = - 1 log 1 – 0 log 0 = 0 high white For attribute Income, Insurance white Info(T) = - ½ log ½ =1 Child black Entropy Income low no no = 0. 9183 Info(Income, T) = ¼ x Info(Thigh) + ¾ x Info(Tlow) = 0. 6887 Gain(Income, T) = Info(T) – Info(Income, T) = 1 – 0. 6887= 0. 3113 For attribute Race, Gain(Race, T) = 0. 1887 For attribute Income, Gain(Income, T) = 0. 3113 COMP 5331 13
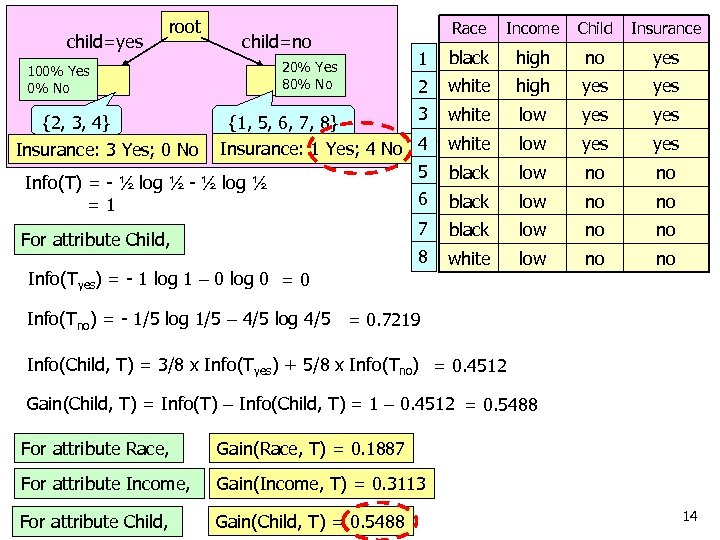
root Race Income Child Insurance 1 black high no yes 2 white high yes 3 {1, 5, 6, 7, 8} Insurance: 1 Yes; 4 No 4 5 Info(T) = - ½ log ½ 6 =1 7 For attribute Child, 8 Info(Tyes) = - 1 log 1 – 0 log 0 = 0 white low yes yes black low no no white low no no child=yes 100% Yes 0% No child=no 20% Yes 80% No {2, 3, 4} Insurance: 3 Yes; 0 No Info(Tno) = - 1/5 log 1/5 – 4/5 log 4/5 = 0. 7219 Info(Child, T) = 3/8 x Info(Tyes) + 5/8 x Info(Tno) = 0. 4512 Gain(Child, T) = Info(T) – Info(Child, T) = 1 – 0. 4512 = 0. 5488 For attribute Race, Gain(Race, T) = 0. 1887 For attribute Income, Gain(Income, T) = 0. 3113 COMP 5331 For attribute Child, Gain(Child, T) = 0. 5488 14
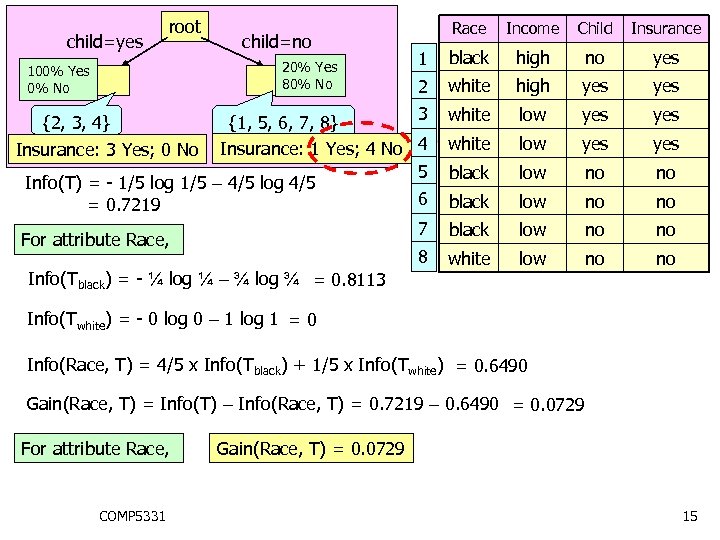
root Race Income Child Insurance 1 black high no yes 2 white high yes 3 {1, 5, 6, 7, 8} Insurance: 1 Yes; 4 No 4 5 Info(T) = - 1/5 log 1/5 – 4/5 log 4/5 6 = 0. 7219 7 For attribute Race, 8 Info(Tblack) = - ¼ log ¼ – ¾ log ¾ = 0. 8113 white low yes yes black low no no white low no no child=yes child=no 20% Yes 80% No 100% Yes 0% No {2, 3, 4} Insurance: 3 Yes; 0 No Info(Twhite) = - 0 log 0 – 1 log 1 = 0 Info(Race, T) = 4/5 x Info(Tblack) + 1/5 x Info(Twhite) = 0. 6490 Gain(Race, T) = Info(T) – Info(Race, T) = 0. 7219 – 0. 6490 = 0. 0729 For attribute Race, COMP 5331 Gain(Race, T) = 0. 0729 15
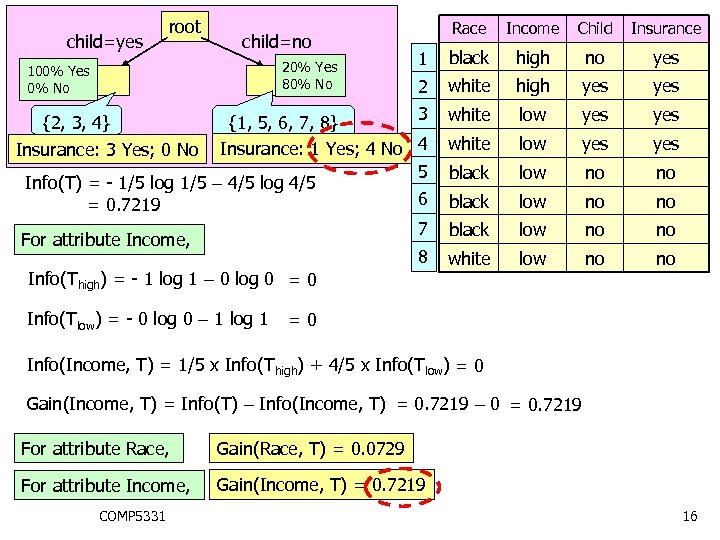
root Race Income Child Insurance 1 black high no yes 2 white high yes 3 {1, 5, 6, 7, 8} Insurance: 1 Yes; 4 No 4 5 Info(T) = - 1/5 log 1/5 – 4/5 log 4/5 6 = 0. 7219 7 For attribute Income, 8 Info(Thigh) = - 1 log 1 – 0 log 0 = 0 white low yes yes black low no no white low no no child=yes child=no 20% Yes 80% No 100% Yes 0% No {2, 3, 4} Insurance: 3 Yes; 0 No Info(Tlow) = - 0 log 0 – 1 log 1 =0 Info(Income, T) = 1/5 x Info(Thigh) + 4/5 x Info(Tlow) = 0 Gain(Income, T) = Info(T) – Info(Income, T) = 0. 7219 – 0 = 0. 7219 For attribute Race, Gain(Race, T) = 0. 0729 For attribute Income, Gain(Income, T) = 0. 7219 COMP 5331 16
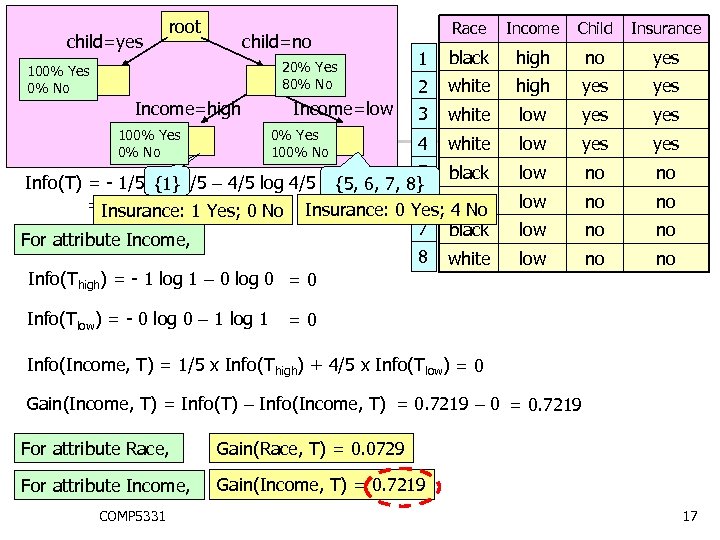
root Race Income Child Insurance 1 black high no yes 2 white high yes 3 white low yes 4 white low yes 5 black Info(T) = - 1/5 log 1/5 – 4/5 log 4/5 {5, 6, 7, 8} {1} 6 =Insurance: 1 Yes; 0 No Insurance: 0 Yes; black 0. 7219 4 No 7 black For attribute Income, 8 white Info(Thigh) = - 1 log 1 – 0 log 0 = 0 low no no child=yes child=no 20% Yes 80% No 100% Yes 0% No Income=high 100% Yes 0% No Income=low 0% Yes 100% No Info(Tlow) = - 0 log 0 – 1 log 1 =0 Info(Income, T) = 1/5 x Info(Thigh) + 4/5 x Info(Tlow) = 0 Gain(Income, T) = Info(T) – Info(Income, T) = 0. 7219 – 0 = 0. 7219 For attribute Race, Gain(Race, T) = 0. 0729 For attribute Income, Gain(Income, T) = 0. 7219 COMP 5331 17
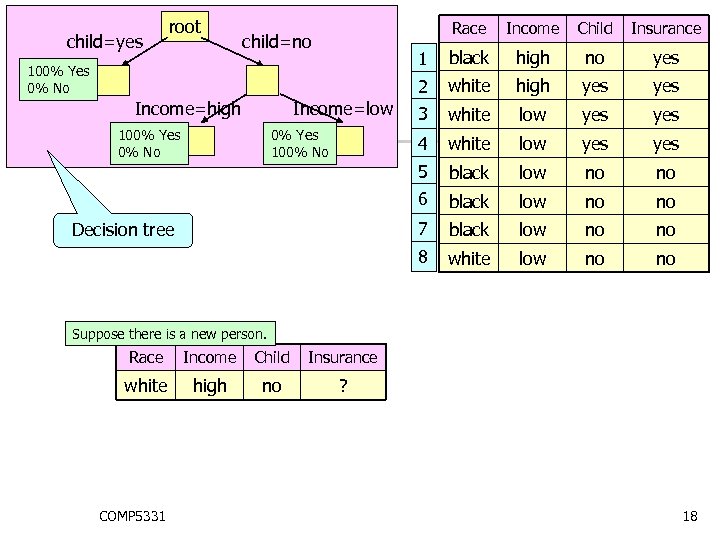
root Race yes white high yes 3 white low yes yes black low no no 8 Decision tree no 7 0% Yes 100% No high 6 100% Yes 0% No black 5 Income=low Income=high Insurance 4 100% Yes 0% No Child 1 child=no Income 2 child=yes white low no no Suppose there is a new person. Race Income Child Insurance white high no ? COMP 5331 18
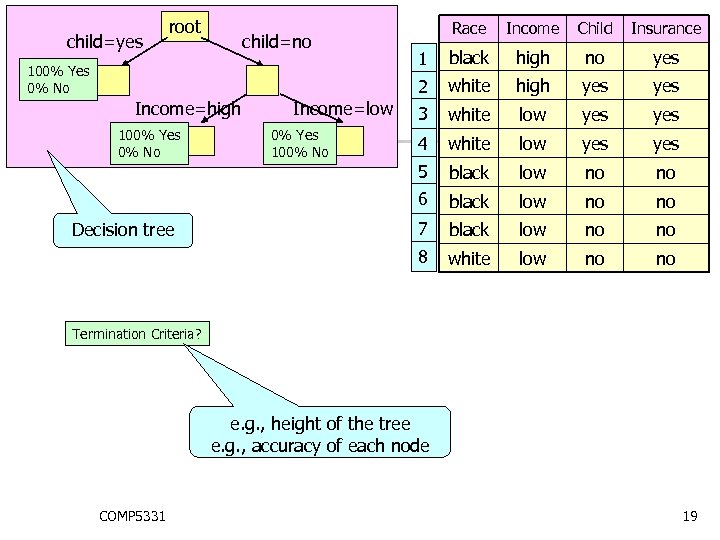
root Decision tree 0% Yes 100% No 1 black high no yes white high yes 3 white low yes 4 white low yes black low no no 8 100% Yes 0% No Income=low Insurance 7 Income=high Child 6 100% Yes 0% No Income 5 child=no Race 2 child=yes white low no no Termination Criteria? e. g. , height of the tree e. g. , accuracy of each node COMP 5331 19

Decision Trees n n n ID 3 C 4. 5 CART COMP 5331 20

C 4. 5 n ID 3 n Impurity Measurement n n Gain(A, T) = Info(T) – Info(A, T) C 4. 5 n Impurity Measurement n n Gain(A, T) = (Info(T) – Info(A, T))/Split. Info(A) where Split. Info(A) = - v A p(v) log p(v) COMP 5331 21

Race no yes high yes low yes white low yes black low no no black Info(Tblack) = - ¾ log ¾ - ¼ log ¼ = 0. 8113 high white For attribute Race, Insurance white Info(T) = - ½ log ½ =1 Child black Entropy Income low no no white low no no Info(Twhite) = - ¾ log ¾ - ¼ log ¼ = 0. 8113 Info(Race, T) = ½ x Info(Tblack) + ½ x Info(Twhite) = 0. 8113 Split. Info(Race) = - ½ log ½ =1 Gain(Race, T) = (Info(T) – Info(Race, T))/Split. Info(Race) = (1 – 0. 8113)/1 = 0. 1887 For attribute Race, COMP 5331 Gain(Race, T) = 0. 1887 22

Race yes high yes yes low yes black low no no black Info(Tlow) = - 1/3 log 1/3 – 2/3 log 2/3 no white low no no white Info(Thigh) = - 1 log 1 – 0 log 0 = 0 high white For attribute Income, Insurance white Info(T) = - ½ log ½ =1 Child black Entropy Income low no no = 0. 9183 Info(Income, T) = ¼ x Info(Thigh) + ¾ x Info(Tlow) = 0. 6887 Split. Info(Income) = - 2/8 log 2/8 – 6/8 log 6/8 = 0. 8113 Gain(Income, T)= (Info(T)–Info(Income, T))/Split. Info(Income) = (1– 0. 6887)/0. 8113 = 0. 3837 Gain(Race, T) = 0. 1887 For attribute Race, For attribute Income, Gain(Income, T) = 0. 3837 COMP 5331 For attribute Child, Gain(Child, T) = ? 23

Decision Trees n n n ID 3 C 4. 5 CART COMP 5331 24

CART n Impurity Measurement n Gini I(P) = 1 – j pj 2 COMP 5331 25

Race Info(Tblack) = 1 – – high yes yes low yes black low no no black = 0. 375 yes low no no black (¼)2 no white (¾)2 high white For attribute Race, Insurance white Info(T) = 1 – (½)2 =½ Child black Gini Income low no no white low no no Info(Twhite) = 1 – (¾)2 – (¼)2 = 0. 375 Info(Race, T) = ½ x Info(Tblack) + ½ x Info(Twhite) = 0. 375 Gain(Race, T) = Info(T) – Info(Race, T) = ½ – 0. 375 = 0. 125 For attribute Race, COMP 5331 Gain(Race, T) = 0. 125 26

Race high no yes high yes yes white low yes black low no no white For attribute Income, Insurance white Info(T) = 1 – (½)2 =½ Child black Gini Income low no no Info(Thigh) = 1 – 12 – 02 = 0 Info(Tlow) = 1 – (1/3)2 – (2/3)2 = 0. 444 Info(Income, T) = 1/4 x Info(Thigh) + 3/4 x Info(Tlow) = 0. 333 Gain(Income, T) = Info(T) – Info(Race, T) = ½ – 0. 333 = 0. 167 For attribute Race, Gain(Race, T) = 0. 125 For attribute Income, Gain(Race, T) = 0. 167 COMP 5331 For attribute Child, Gain(Child, T) = ? 27

Classification Methods n n n Decision Tree Bayesian Classifier Nearest Neighbor Classifier COMP 5331 28

Bayesian Classifier n n Naïve Bayes Classifier Bayesian Belief Networks COMP 5331 29

Naïve Bayes Classifier n n n Statistical Classifiers Probabilities Conditional probabilities COMP 5331 30

Naïve Bayes Classifier n Conditional Probability n n A: a random variable B: a random variable n P(A | B) = COMP 5331 P(AB) P(B) 31

Naïve Bayes Classifier n Bayes Rule n n A : a random variable B: a random variable n P(A | B) = COMP 5331 P(B|A) P(B) 32

Race Income Child Insurance black high no yes white high yes yes Naïve Bayes Classifierlow white yes black low no no white n low no no Independent Assumption n n Each attribute are independent e. g. , P(X, Y, Z | A) = P(X | A) x P(Y | A) x P(Z | A) COMP 5331 33
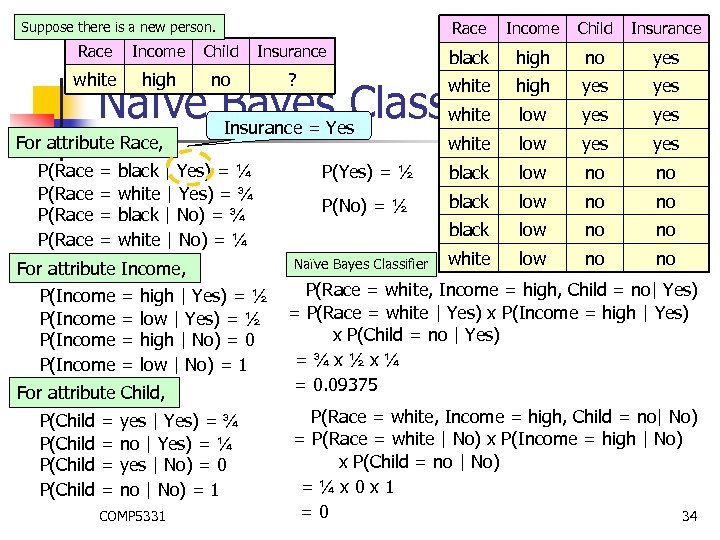
Race Suppose there is a new person. Income Child Insurance Race Income Child Insurance black high no yes white high no ? white high Naïve Bayes. Yes. Classifierlow white Insurance = yes yes = = For attribute Race, P(Race black | Yes) = ¼ white | Yes) = ¾ black | No) = ¾ white | No) = ¼ For attribute Income, P(Income = = high | Yes) = ½ low | Yes) = ½ high | No) = 0 low | No) = 1 For attribute Child, P(Child = = yes | Yes) = ¾ no | Yes) = ¼ yes | No) = 0 no | No) = 1 COMP 5331 white low yes P(Yes) = ½ black low no no P(No) = ½ black low no no white low no no Naïve Bayes Classifier P(Race = white, Income = high, Child = no| Yes) = P(Race = white | Yes) x P(Income = high | Yes) x P(Child = no | Yes) =¾x½x¼ = 0. 09375 P(Race = white, Income = high, Child = no| No) = P(Race = white | No) x P(Income = high | No) x P(Child = no | No) =¼x 0 x 1 =0 34
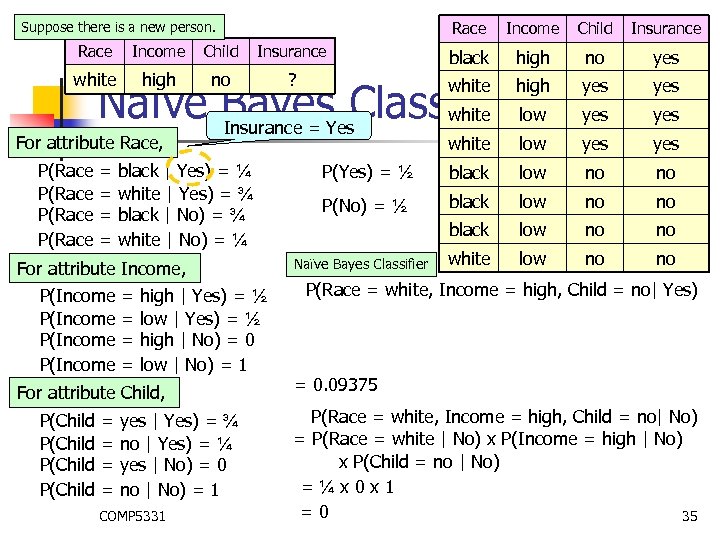
Race Suppose there is a new person. Income Child Insurance Race Income Child Insurance black high no yes white high no ? white high Naïve Bayes. Yes. Classifierlow white Insurance = yes yes = = For attribute Race, P(Race black | Yes) = ¼ white | Yes) = ¾ black | No) = ¾ white | No) = ¼ For attribute Income, P(Income = = high | Yes) = ½ low | Yes) = ½ high | No) = 0 low | No) = 1 For attribute Child, P(Child = = yes | Yes) = ¾ no | Yes) = ¼ yes | No) = 0 no | No) = 1 COMP 5331 white low yes P(Yes) = ½ black low no no P(No) = ½ black low no no white low no no Naïve Bayes Classifier P(Race = white, Income = high, Child = no| Yes) = 0. 09375 P(Race = white, Income = high, Child = no| No) = P(Race = white | No) x P(Income = high | No) x P(Child = no | No) =¼x 0 x 1 =0 35
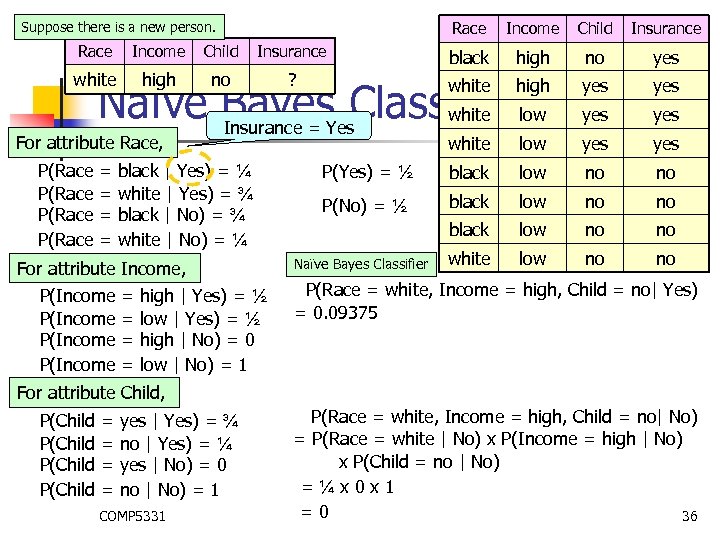
Race Suppose there is a new person. Income Child Insurance Race Income Child Insurance black high no yes white high no ? white high Naïve Bayes. Yes. Classifierlow white Insurance = yes yes = = For attribute Race, P(Race black | Yes) = ¼ white | Yes) = ¾ black | No) = ¾ white | No) = ¼ For attribute Income, P(Income = = high | Yes) = ½ low | Yes) = ½ high | No) = 0 low | No) = 1 white low yes P(Yes) = ½ black low no no P(No) = ½ black low no no white low no no Naïve Bayes Classifier P(Race = white, Income = high, Child = no| Yes) = 0. 09375 For attribute Child, P(Child = = yes | Yes) = ¾ no | Yes) = ¼ yes | No) = 0 no | No) = 1 COMP 5331 P(Race = white, Income = high, Child = no| No) = P(Race = white | No) x P(Income = high | No) x P(Child = no | No) =¼x 0 x 1 =0 36
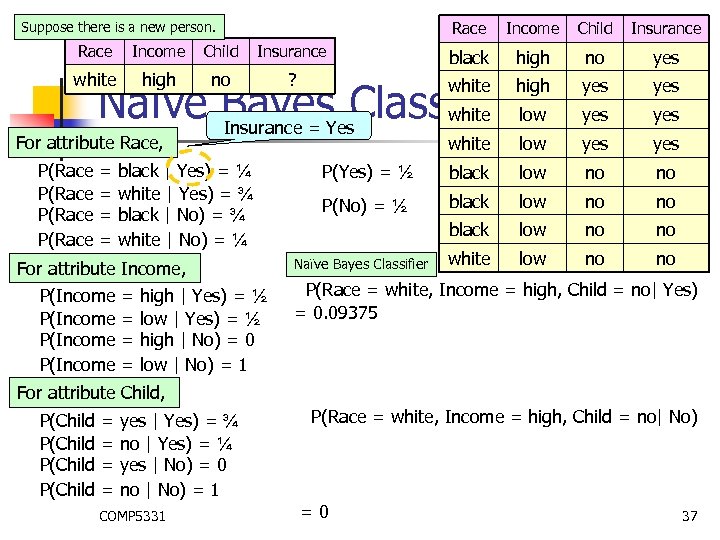
Race Suppose there is a new person. Income Child Insurance Race Income Child Insurance black high no yes white high no ? white high Naïve Bayes. Yes. Classifierlow white Insurance = yes yes = = For attribute Race, P(Race black | Yes) = ¼ white | Yes) = ¾ black | No) = ¾ white | No) = ¼ For attribute Income, P(Income = = high | Yes) = ½ low | Yes) = ½ high | No) = 0 low | No) = 1 white low yes P(Yes) = ½ black low no no P(No) = ½ black low no no white low no no Naïve Bayes Classifier P(Race = white, Income = high, Child = no| Yes) = 0. 09375 For attribute Child, P(Child = = yes | Yes) = ¾ no | Yes) = ¼ yes | No) = 0 no | No) = 1 COMP 5331 P(Race = white, Income = high, Child = no| No) =0 37
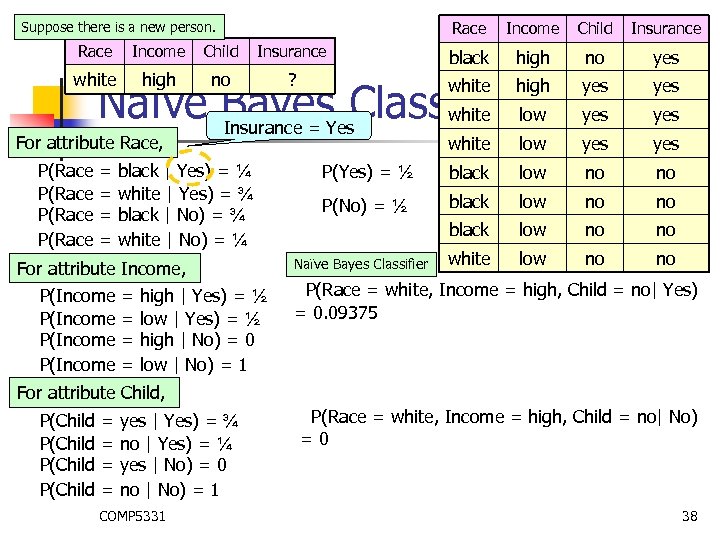
Race Suppose there is a new person. Income Child Insurance Race Income Child Insurance black high no yes white high no ? white high Naïve Bayes. Yes. Classifierlow white Insurance = yes yes = = For attribute Race, P(Race black | Yes) = ¼ white | Yes) = ¾ black | No) = ¾ white | No) = ¼ For attribute Income, P(Income = = high | Yes) = ½ low | Yes) = ½ high | No) = 0 low | No) = 1 white low yes P(Yes) = ½ black low no no P(No) = ½ black low no no white low no no Naïve Bayes Classifier P(Race = white, Income = high, Child = no| Yes) = 0. 09375 For attribute Child, P(Child = = yes | Yes) = ¾ no | Yes) = ¼ yes | No) = 0 no | No) = 1 COMP 5331 P(Race = white, Income = high, Child = no| No) =0 38
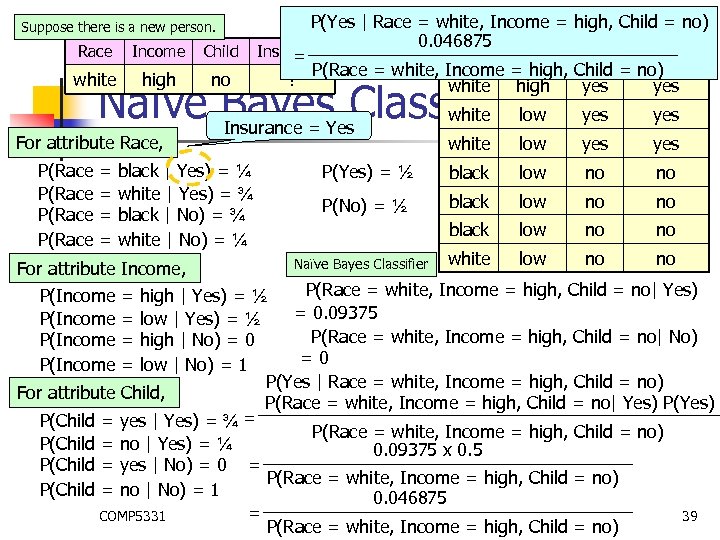
Suppose there is a new person. Race Income Child white high no P(Yes | Race = white, Income = high, Child = no) Race Income Child Insurance 0. 046875 Insurance = black high no yes P(Race = white, Income = high, Child = no) ? white high yes Naïve Bayes. Yes. Classifierlow white Insurance = For attribute Race, P(Race = = black | Yes) = ¼ white | Yes) = ¾ black | No) = ¾ white | No) = ¼ For attribute Income, yes white low yes P(Yes) = ½ black low no no P(No) = ½ black low no no white low no no Naïve Bayes Classifier P(Race = white, Income = high, Child = no| Yes) high | Yes) = ½ = 0. 09375 low | Yes) = ½ P(Race = white, Income = high, Child = no| No) high | No) = 0 =0 low | No) = 1 P(Yes | Race = white, Income = high, Child = no) For attribute Child, P(Race = white, Income = high, Child = no| Yes) P(Yes) = P(Child = yes | Yes) = ¾ P(Race = white, Income = high, Child = no) P(Child = no | Yes) = ¼ 0. 09375 x 0. 5 P(Child = yes | No) = 0 = P(Race = white, Income = high, Child = no) P(Child = no | No) = 1 0. 046875 = COMP 5331 39 P(Race = white, Income = high, Child = no) P(Income = =
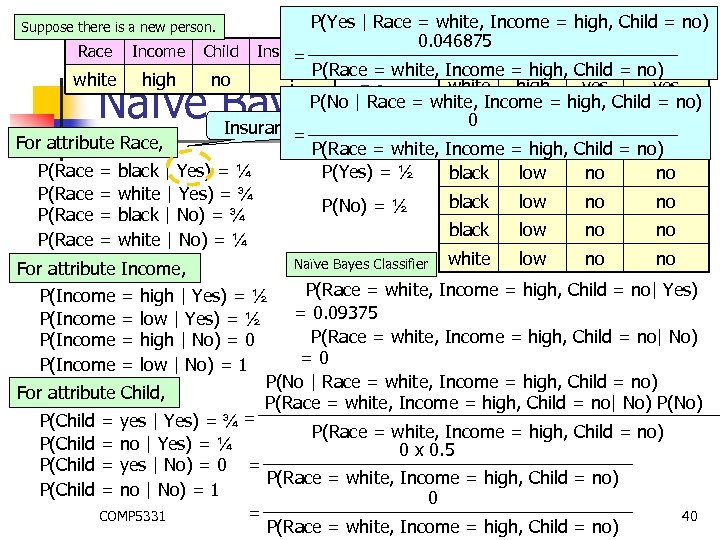
P(Yes | Race = white, Income = high, Child = no) Race Income Child Insurance 0. 046875 Race Income Child Insurance = black high no yes P(Race = white, Income = high, Child = no) white high no ? white high yes P(No | Race = white, Income = high, Child = no) white low yes 0 Insurance = Yes = For attribute Race, white low yes P(Race = white, Income = high, Child = no) P(Race = black | Yes) = ¼ P(Yes) = ½ black low no no P(Race = white | Yes) = ¾ black low no no P(No) = ½ P(Race = black | No) = ¾ black low no no P(Race = white | No) = ¼ low no no Naïve Bayes Classifier white For attribute Income, P(Race = white, Income = high, Child = no| Yes) P(Income = high | Yes) = ½ = 0. 09375 P(Income = low | Yes) = ½ P(Race = white, Income = high, Child = no| No) P(Income = high | No) = 0 =0 P(Income = low | No) = 1 P(No | Race = white, Income = high, Child = no) For attribute Child, P(Race = white, Income = high, Child = no| No) P(No) = P(Child = yes | Yes) = ¾ P(Race = white, Income = high, Child = no) P(Child = no | Yes) = ¼ 0 x 0. 5 P(Child = yes | No) = 0 = P(Race = white, Income = high, Child = no) P(Child = no | No) = 1 0 = COMP 5331 40 P(Race = white, Income = high, Child = no) Suppose there is a new person. Naïve Bayes Classifier
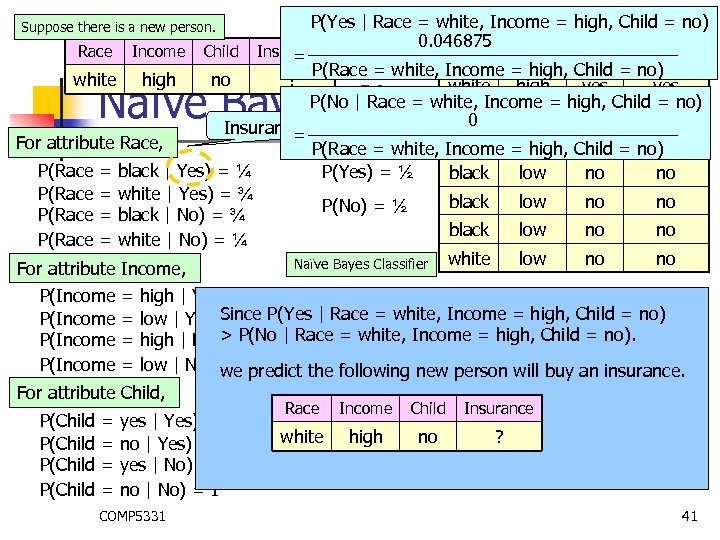
P(Yes | Race = white, Income = high, Child = no) Race Income Child Insurance 0. 046875 Race Income Child Insurance = black high no yes P(Race = white, Income = high, Child = no) white high no ? white high yes P(No | Race = white, Income = high, Child = no) white low yes 0 Insurance = Yes = For attribute Race, white low yes P(Race = white, Income = high, Child = no) P(Race = black | Yes) = ¼ P(Yes) = ½ black low no no P(Race = white | Yes) = ¾ black low no no P(No) = ½ P(Race = black | No) = ¾ black low no no P(Race = white | No) = ¼ low no no Naïve Bayes Classifier white For attribute Income, Suppose there is a new person. Naïve Bayes Classifier P(Income = = high | Yes) = ½ low | Yes)Since P(Yes | Race = white, Income = high, Child = no) =½ high | No)> P(No | Race = white, Income = high, Child = no). =0 low | No) = 1 predict the following new person will buy an insurance. we For attribute Child, P(Child = = yes | Yes) = ¾ no | Yes) = ¼ yes | No) = 0 no | No) = 1 COMP 5331 Race Income Child Insurance white high no ? 41

Bayesian Classifier n n Naïve Bayes Classifier Bayesian Belief Networks COMP 5331 42

Bayesian Belief Network n Naïve Bayes Classifier n n Independent Assumption Bayesian Belief Network n Do not have independent assumption COMP 5331 43
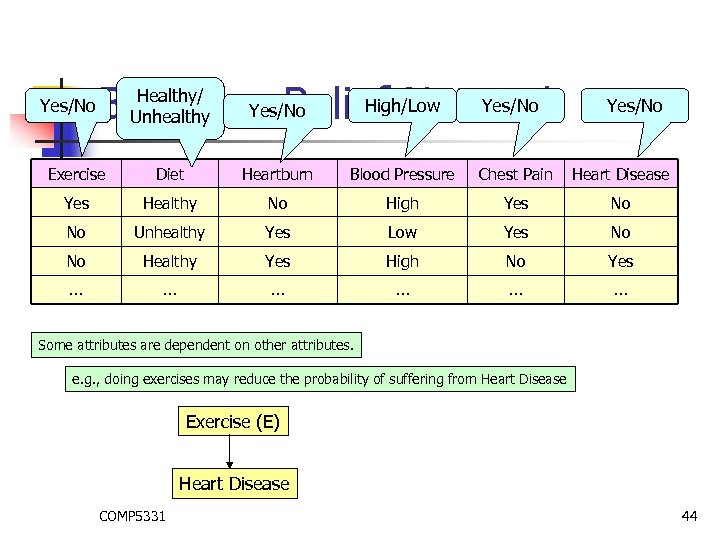
Yes/No High/Low Yes/No Bayesian Belief Network Healthy/ Unhealthy Yes/No Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease Yes Healthy No High Yes No No Unhealthy Yes Low Yes No No Healthy Yes High No Yes … … … Some attributes are dependent on other attributes. e. g. , doing exercises may reduce the probability of suffering from Heart Disease Exercise (E) Heart Disease COMP 5331 44
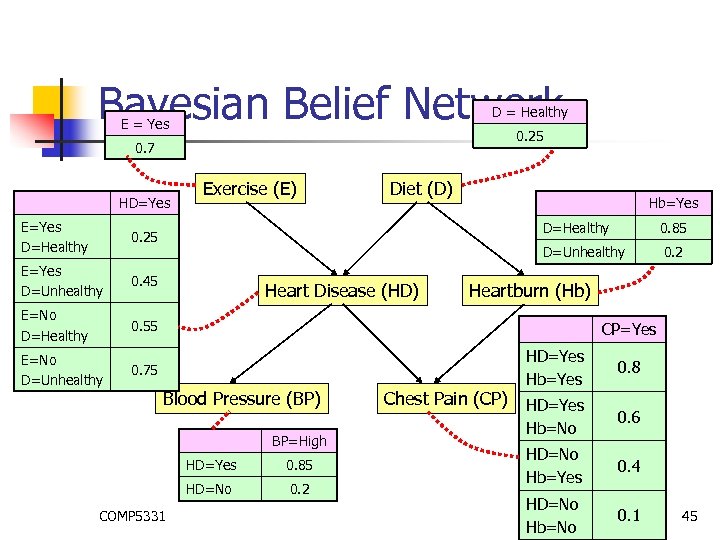
Bayesian Belief Network D = Healthy E = Yes 0. 25 0. 7 HD=Yes E=Yes D=Healthy 0. 45 E=No D=Healthy Hb=Yes 0. 55 E=No D=Unhealthy Diet (D) 0. 25 E=Yes D=Unhealthy Exercise (E) 0. 75 D=Healthy D=Unhealthy Heart Disease (HD) 0. 85 0. 2 Heartburn (Hb) CP=Yes Blood Pressure (BP) BP=High HD=Yes HD=No COMP 5331 0. 85 0. 2 Chest Pain (CP) HD=Yes Hb=Yes 0. 8 HD=Yes Hb=No 0. 6 HD=No Hb=Yes 0. 4 HD=No Hb=No 0. 1 45

Let X, Y, Z be three random variables. X is said to be conditionally independent of Y given Z if the following holds. P(X | Y, Z) = P(X | Z) Bayesian Belief Network Lemma: If X is conditionally independent of Y given Z, P(X, Y | Z) = P(X | Z) x P(Y | Z) ? COMP 5331 46
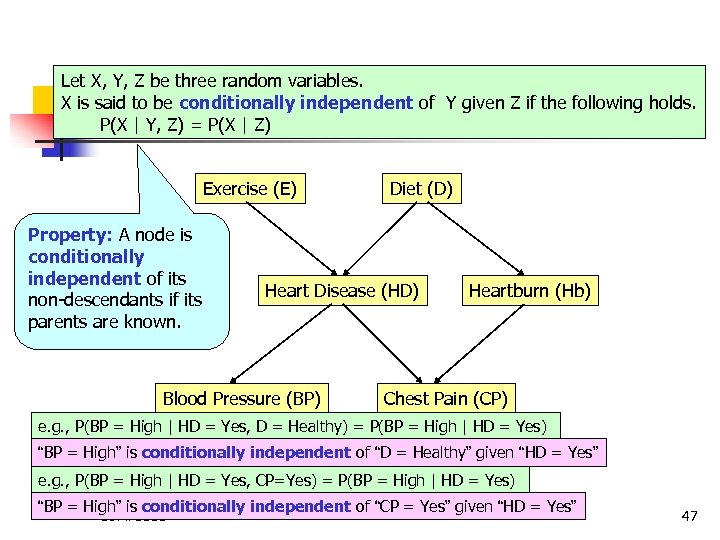
Let X, Y, Z be three random variables. X is said to be conditionally independent of Y given Z if the following holds. P(X | Y, Z) = P(X | Z) Bayesian Belief Network Exercise (E) Property: A node is conditionally independent of its non-descendants if its parents are known. Diet (D) Heart Disease (HD) Blood Pressure (BP) Heartburn (Hb) Chest Pain (CP) e. g. , P(BP = High | HD = Yes, D = Healthy) = P(BP = High | HD = Yes) “BP = High” is conditionally independent of “D = Healthy” given “HD = Yes” e. g. , P(BP = High | HD = Yes, CP=Yes) = P(BP = High | HD = Yes) “BP = High” is conditionally independent of “CP = Yes” given “HD = Yes” COMP 5331 47
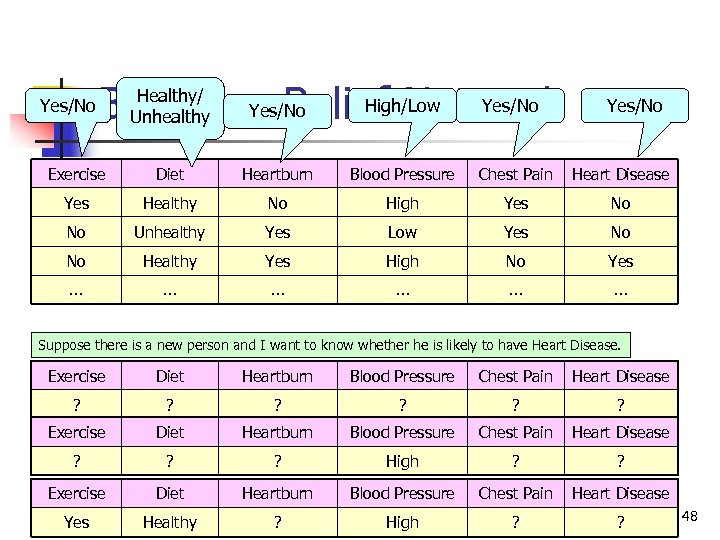
Yes/No High/Low Yes/No Bayesian Belief Network Healthy/ Unhealthy Yes/No Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease Yes Healthy No High Yes No No Unhealthy Yes Low Yes No No Healthy Yes High No Yes … … … Suppose there is a new person and I want to know whether he is likely to have Heart Disease. Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease ? ? ? High ? ? Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease ? High ? ? Yes COMP 5331 Healthy 48

Suppose there is a new person and I want to know whether he is likely to have Heart Disease. Bayesian Belief Network Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease ? ? ? P(HD = Yes) = x {Yes, No} y {Healthy, Unhealthy} P(HD=Yes|E=x, D=y) x P(E=x, D=y) = x {Yes, No} y {Healthy, Unhealthy} P(HD=Yes|E=x, D=y) x P(E=x) x P(D=y) = 0. 25 x 0. 7 x 0. 25 + 0. 45 x 0. 75 + 0. 55 x 0. 3 x 0. 25 + 0. 75 x 0. 3 x 0. 75 = 0. 49 P(HD = No) = 1 - P(HD = Yes) = 1 - 0. 49 = 0. 51 COMP 5331 49

Suppose there is a new person and I want to know whether he is likely to have Heart Disease. Bayesian Belief Network Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease ? ? ? High ? ? P(BP = High) = x {Yes, No} P(BP = High|HD=x) x P(HD = x) = 0. 85 x 0. 49 + 0. 2 x 0. 51 = 0. 5185 P(HD = Yes|BP = High) = = P(BP = High|HD=Yes) x P(HD = Yes) P(BP = High) 0. 85 x 0. 49 0. 5185 = 0. 8033 P(HD = No|BP = High) = 1 – P(HD = Yes|BP = High) = 1 – 0. 8033 = 0. 1967 COMP 5331 50
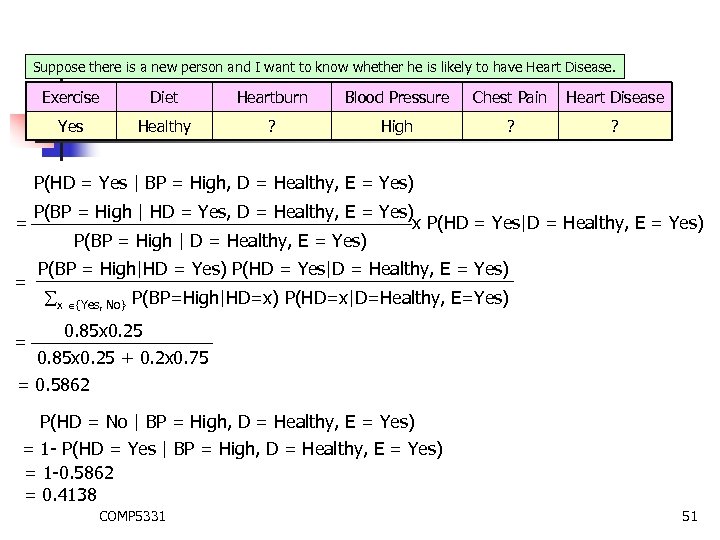
Suppose there is a new person and I want to know whether he is likely to have Heart Disease. Bayesian Belief Network Exercise Diet Heartburn Blood Pressure Chest Pain Heart Disease Yes Healthy ? High ? ? P(HD = Yes | BP = High, D = Healthy, E = Yes) = = = P(BP = High | HD = Yes, D = Healthy, E = Yes) x P(HD = Yes|D = Healthy, E = Yes) P(BP = High | D = Healthy, E = Yes) P(BP = High|HD = Yes) P(HD = Yes|D = Healthy, E = Yes) x {Yes, No} P(BP=High|HD=x) P(HD=x|D=Healthy, E=Yes) 0. 85 x 0. 25 + 0. 2 x 0. 75 = 0. 5862 P(HD = No | BP = High, D = Healthy, E = Yes) = 1 - P(HD = Yes | BP = High, D = Healthy, E = Yes) = 1 -0. 5862 = 0. 4138 COMP 5331 51

Classification Methods n n n Decision Tree Bayesian Classifier Nearest Neighbor Classifier COMP 5331 52
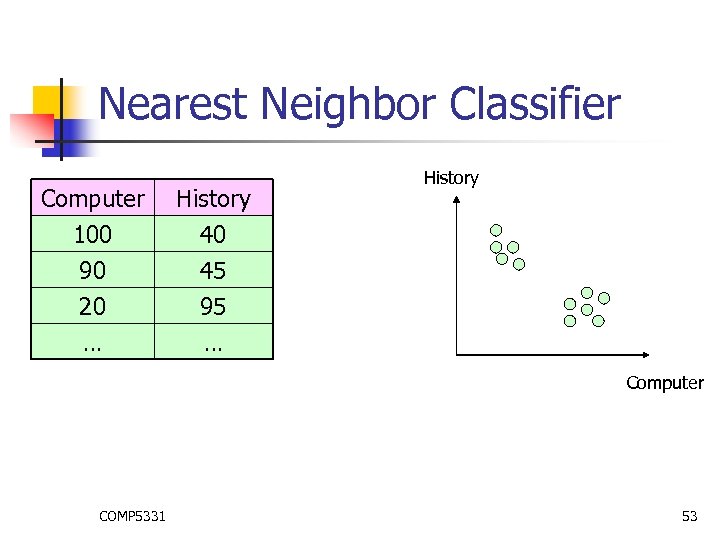
Nearest Neighbor Classifier Computer 100 90 20 History 40 45 95 … History … Computer COMP 5331 53
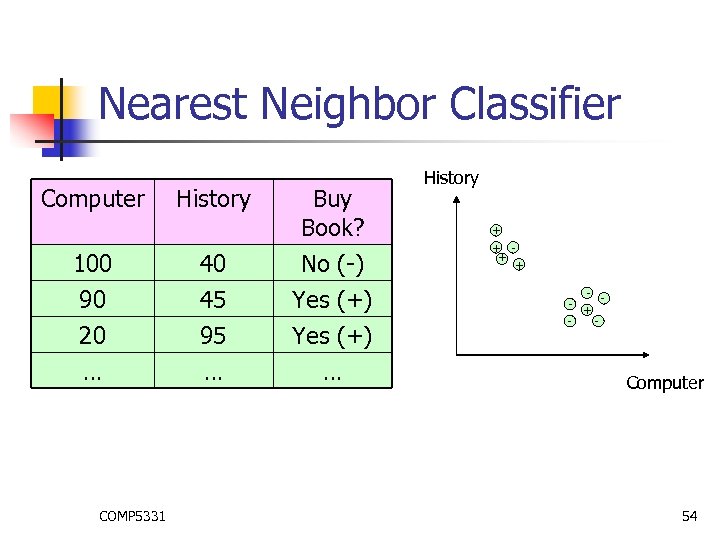
Nearest Neighbor Classifier Computer History Buy Book? 100 40 No (-) 90 20 … 45 95 … Yes (+) … COMP 5331 History + + - + - Computer 54
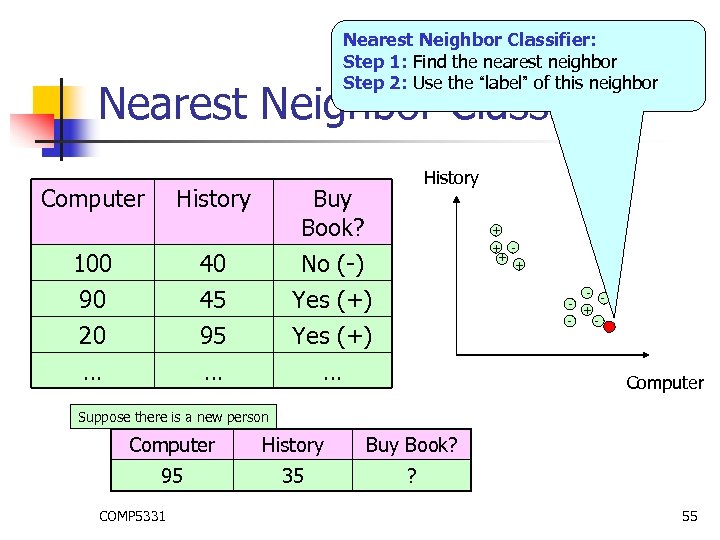
Nearest Neighbor Classifier: Step 1: Find the nearest neighbor Step 2: Use the “label” of this neighbor Nearest Neighbor Classifier Computer History Buy Book? + + 100 40 No (-) 90 20 … 45 95 … Yes (+) … - + - Computer Suppose there is a new person Computer History Buy Book? 95 35 ? COMP 5331 55
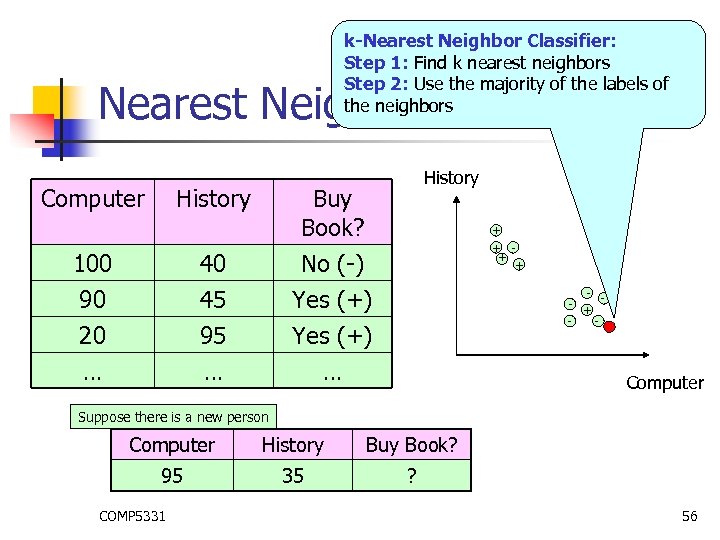
k-Nearest Neighbor Classifier: Step 1: Find k nearest neighbors Step 2: Use the majority of the labels of the neighbors Nearest Neighbor Classifier Computer History Buy Book? + + 100 40 No (-) 90 20 … 45 95 … Yes (+) … - + - Computer Suppose there is a new person Computer History Buy Book? 95 35 ? COMP 5331 56
611baef201b3236bf918dbf477623137.ppt