Communications Networking and Signal Processing Wireless Foundations Faculty

Communications, Networking, and Signal Processing Wireless Foundations Faculty May 20, 2008

Grand Challenges • Capacity of wireless networks – Abstraction of physical resources – Scalability – Architecture • Communication, Computation and Control – Communicate to compute – Compute to communicate – Control/Sense/Estimate • Active social networks: towards Web 4. 0 – Human free will and actions in the world – Incentives and semantics

• Venkat Anantharam • Michael Gastpar • Kannan Ramchandran • Anant Sahai • David Tse • Martin Wainwright Long term research: focus on signal processing, information theory, and fundamental limits. Interface to economics and policy.

Here be dragons! Our weapons: • • • Information theory Robust control and signal processing Learning and distributed adaptation Game theory and economics And any other sharp enough blade …

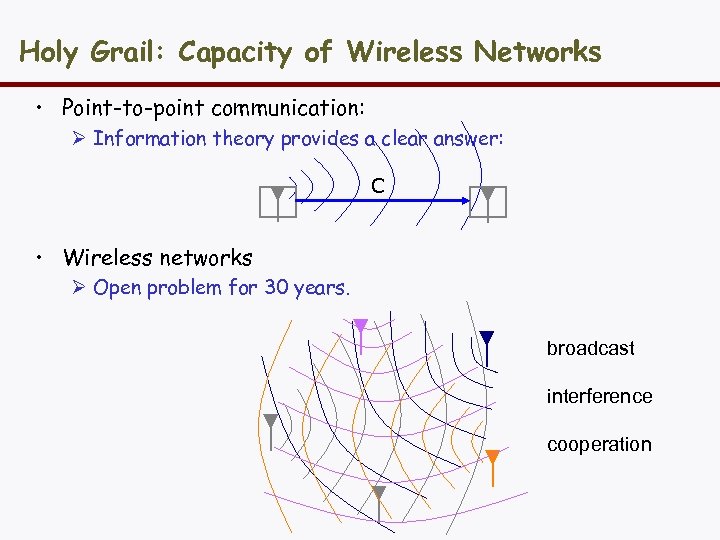Holy Grail: Capacity of Wireless Networks • Point-to-point communication: Ø Information theory provides a clear answer: C • Wireless networks Ø Open problem for 30 years. broadcast interference cooperation

Two Key Questions • Is there a simple abstraction of the physical layer? • Are there big gains to be had under optimal cooperation?

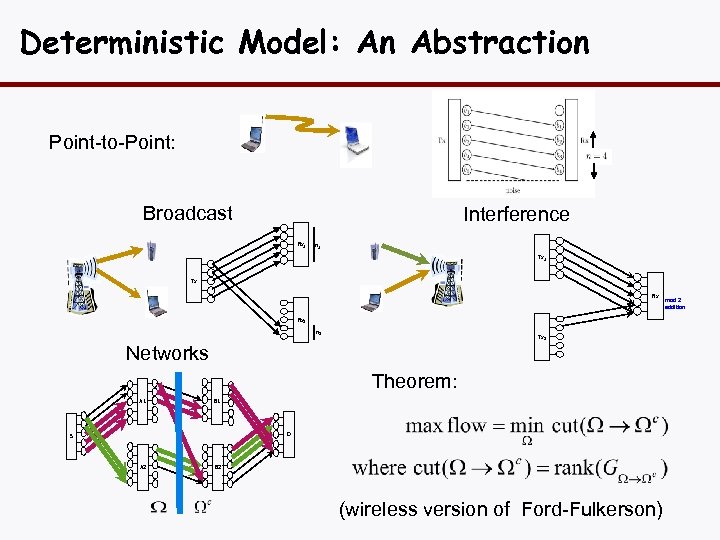Deterministic Model: An Abstraction Point-to-Point: Broadcast Interference Rx 1 n 1 Tx + Rx 2 n 2 Tx 2 Networks Theorem: A 1 B 1 D S A 2 B 2 (wireless version of Ford-Fulkerson) mod 2 addition

Bridging the Gap Higher Layers PHY Layer deterministic model

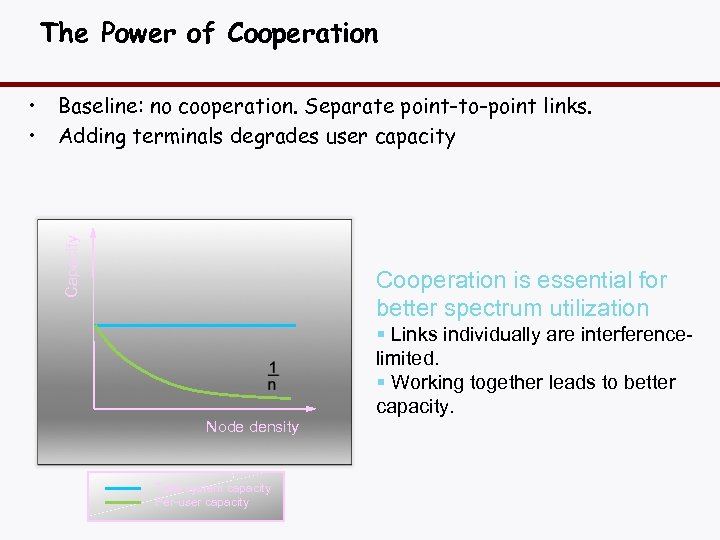The Power of Cooperation Baseline: no cooperation. Separate point-to-point links. Adding terminals degrades user capacity Capacity • • Cooperation is essential for better spectrum utilization Node density Total system capacity Per-user capacity § Links individually are interferencelimited. § Working together leads to better capacity.

The Power of Cooperation Capacity Packet Multi-hop Wireless Meshes Node density [Ref: Gupta/Kumar’ 00] • shorter-range to reduce interference • a network effect [Courtesy: R. Chandra, Microsoft Research]

The Power of Cooperation Capacity Ultimate Cooperation Cooperative MIMO Node density [Ref: Ozgur/Leveque/Tse’ 07] § Construct large effective-aperture antenna array by combining many terminals, § simultaneous transmission of many streams over longer range § hierarchical cooperation minimizes overhead

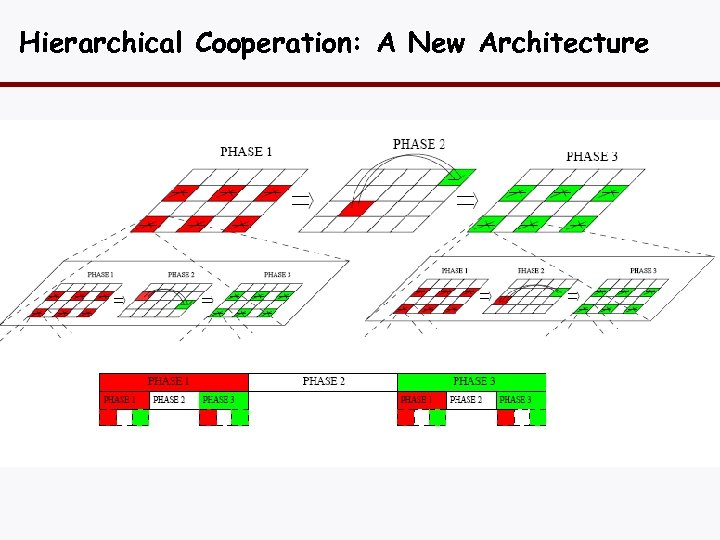Hierarchical Cooperation: A New Architecture

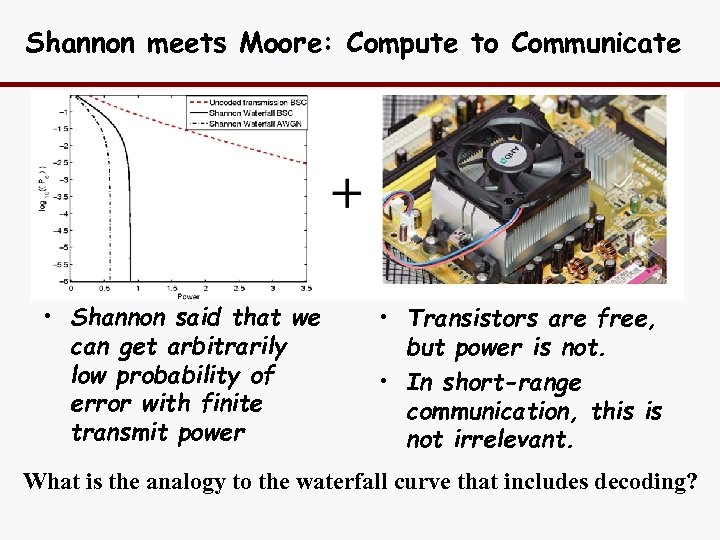Shannon meets Moore: Compute to Communicate • Shannon said that we can get arbitrarily low probability of error with finite transmit power • Transistors are free, but power is not. • In short-range communication, this is not irrelevant. What is the analogy to the waterfall curve that includes decoding?

The need for guidance • Practical question: “What should we deploy in 2010, 2015, or 2020? ” – Semiconductor side: roadmap + scaling – Gives an ability to plan and coordinate work across different levels. • No such connection on the comm. side. – Capacity calculations do not say anything about complexity and power. – Left to either guess, stick to tried/true approaches, or to invest a lot of engineering effort to even understand plausibility. • Need a path to connect to the roadmap.

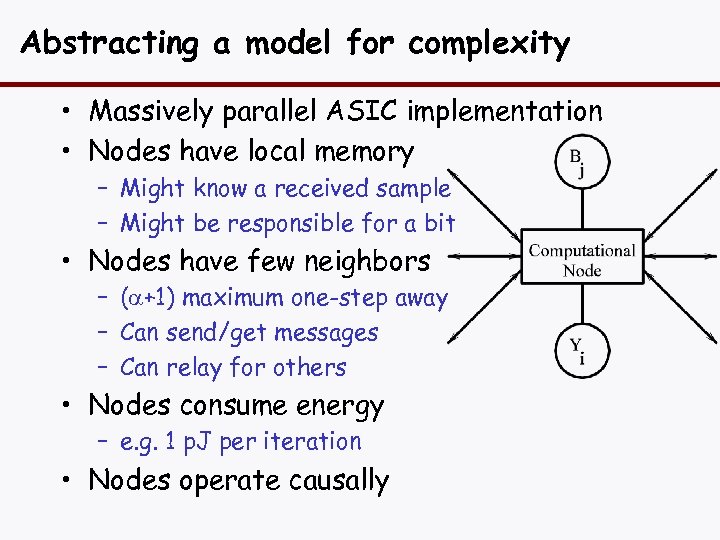Abstracting a model for complexity • Massively parallel ASIC implementation • Nodes have local memory – Might know a received sample – Might be responsible for a bit • Nodes have few neighbors – (a+1) maximum one-step away – Can send/get messages – Can relay for others • Nodes consume energy – e. g. 1 p. J per iteration • Nodes operate causally

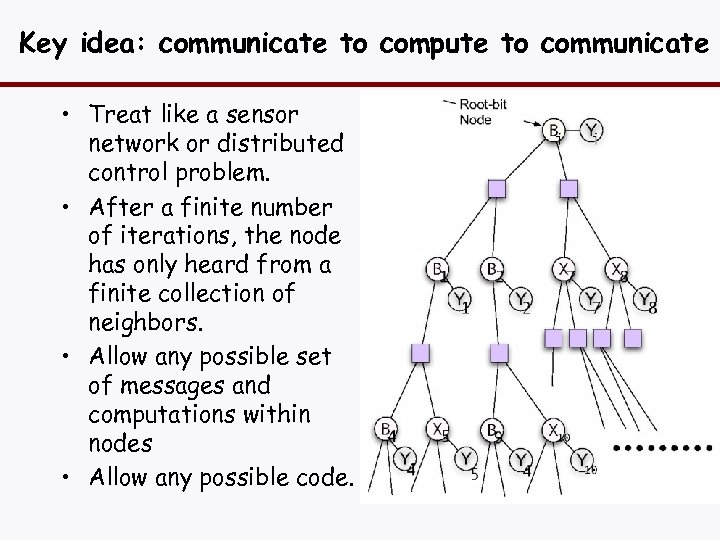Key idea: communicate to compute to communicate • Treat like a sensor network or distributed control problem. • After a finite number of iterations, the node has only heard from a finite collection of neighbors. • Allow any possible set of messages and computations within nodes • Allow any possible code.

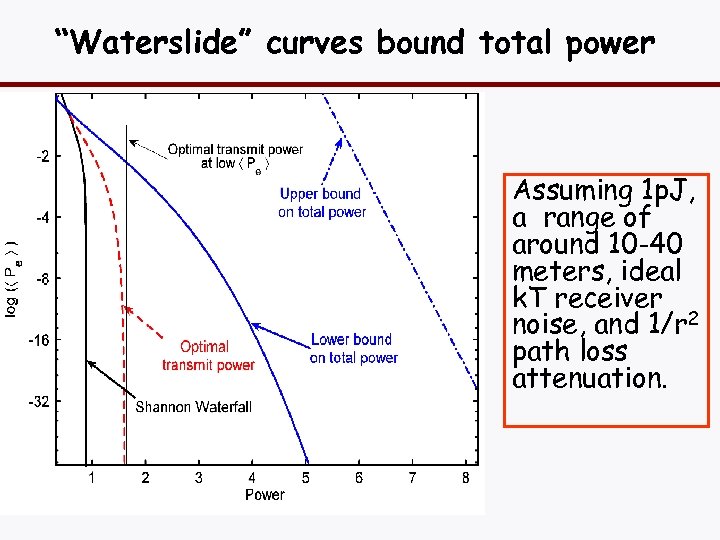“Waterslide” curves bound total power Assuming 1 p. J, a range of around 10 -40 meters, ideal k. T receiver noise, and 1/r 2 path loss attenuation.

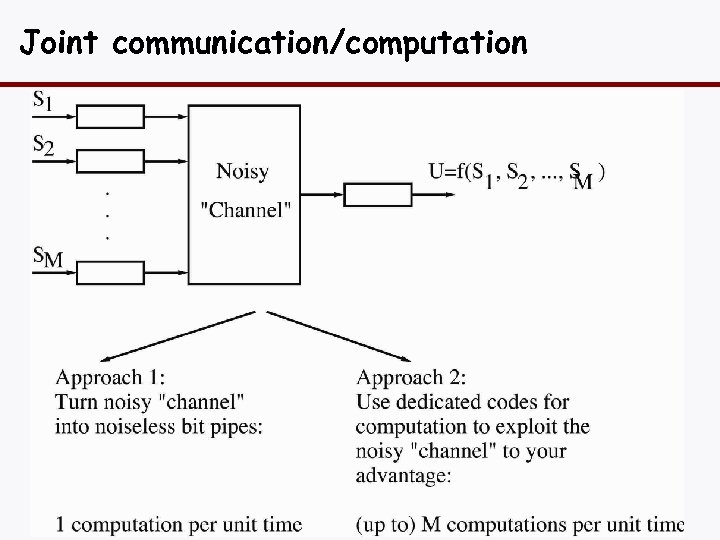Joint communication/computation

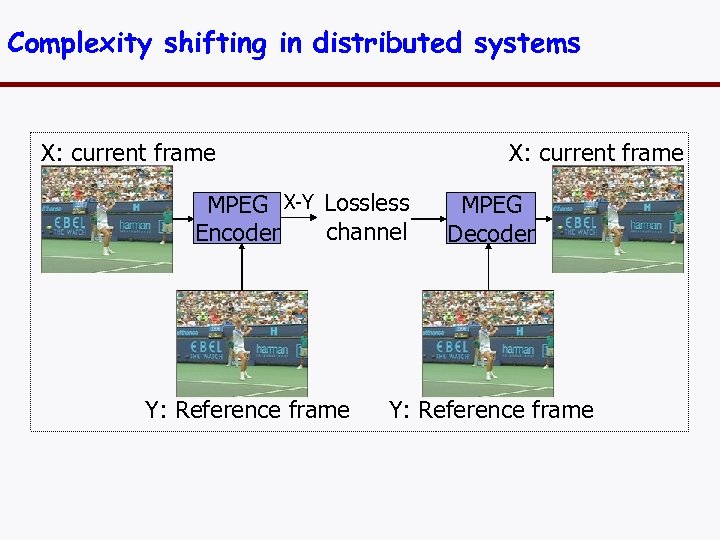Complexity shifting in distributed systems X: current frame MPEG X-Y Lossless channel Encoder Y: Reference frame MPEG Decoder Y: Reference frame

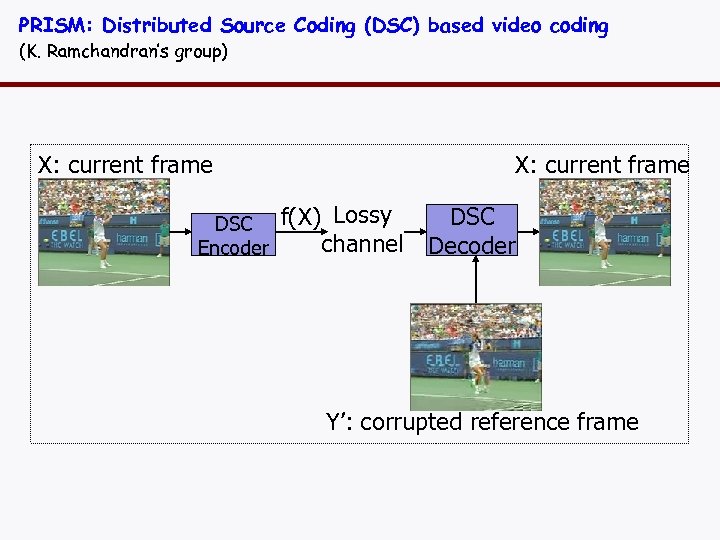PRISM: Distributed Source Coding (DSC) based video coding (K. Ramchandran’s group) X: current frame DSC Encoder X: current frame f(X) Lossy channel DSC Decoder Y’: corrupted reference frame

Spectrum: The Looming Future • Many heterogeneous wireless systems share the entire spectrum in a flexible and on-demand basis. • How to get from here to there?

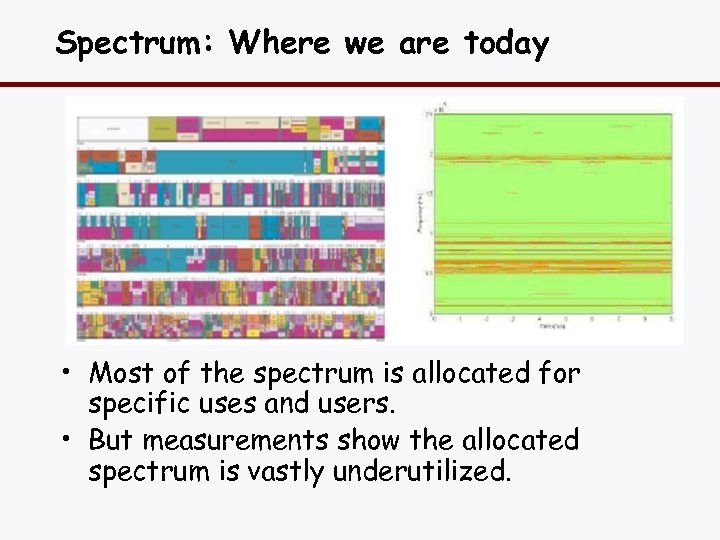Spectrum: Where we are today • Most of the spectrum is allocated for specific uses and users. • But measurements show the allocated spectrum is vastly underutilized.

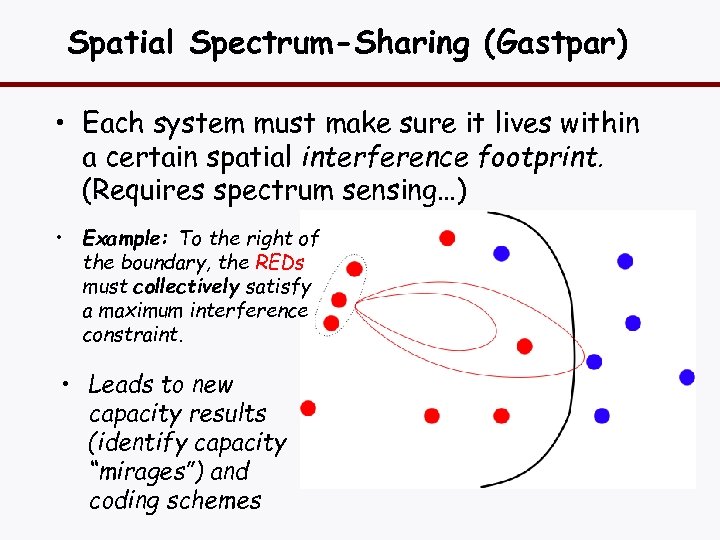Spatial Spectrum-Sharing (Gastpar) • Each system must make sure it lives within a certain spatial interference footprint. (Requires spectrum sensing…) • Example: To the right of the boundary, the REDs must collectively satisfy a maximum interference constraint. • Leads to new capacity results (identify capacity “mirages”) and coding schemes

Disneyland vs Yosemite: the policy dimension • Owner controls access to preserve Qo. S for users • “Band-managers” own band lease it out. • Monopoly • Public owns and sets guidelines for use • Unlicensed users are on their own • Competition “Spectrum tour guide” can coordinate users without band ownership

Cognitive Radio Slides Follow

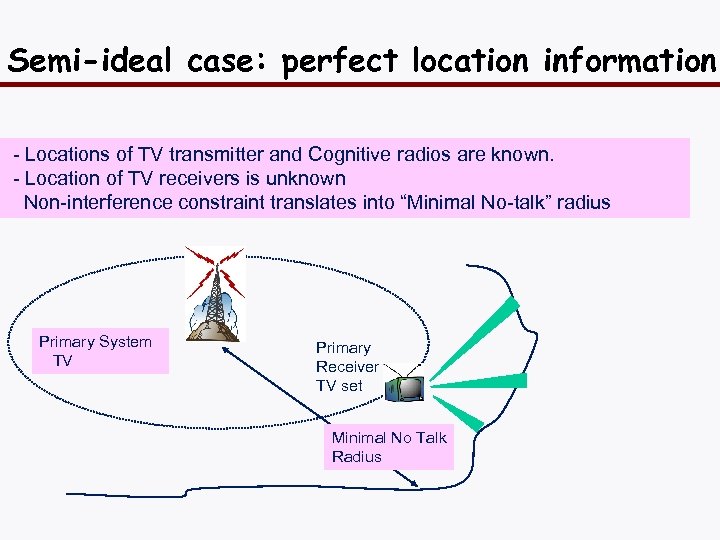Semi-ideal case: perfect location information - Locations of TV transmitter and Cognitive radios are known. - Location of TV receivers is unknown Non-interference constraint translates into “Minimal No-talk” radius Primary System TV Primary Receiver TV set Minimal No Talk Radius

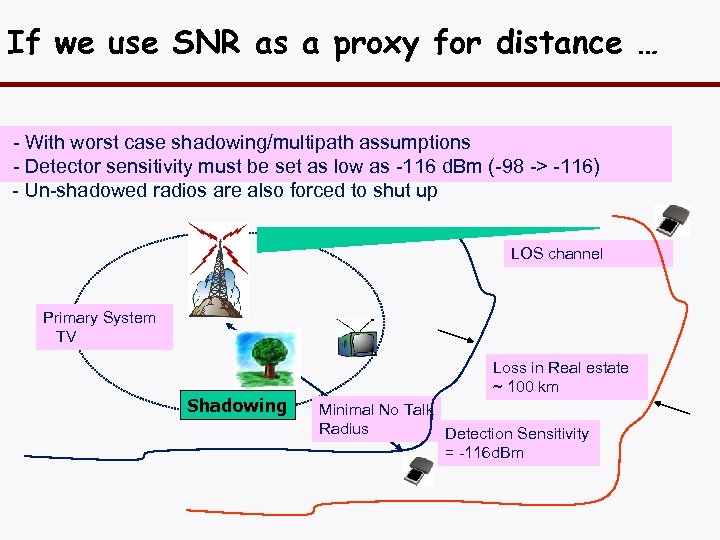If we use SNR as a proxy for distance … - With worst case shadowing/multipath assumptions - Detector sensitivity must be set as low as -116 d. Bm (-98 -> -116) - Un-shadowed radios are also forced to shut up LOS channel Primary System TV Shadowing Loss in Real estate ~ 100 km Minimal No Talk Radius Detection Sensitivity = -116 d. Bm

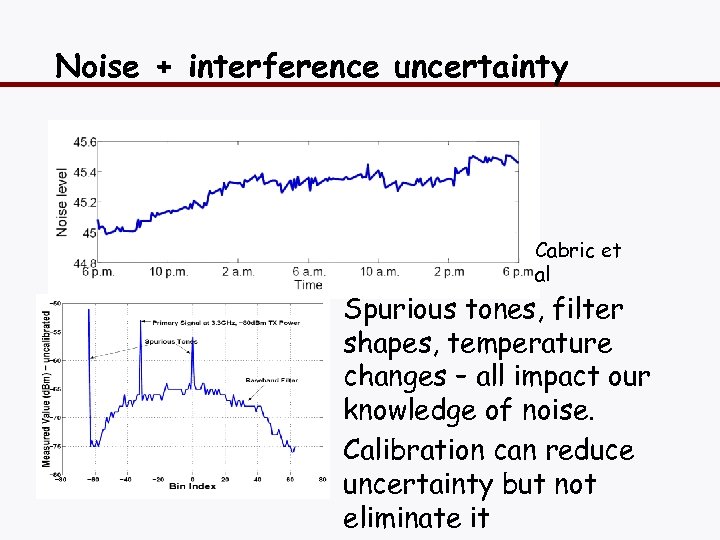Noise + interference uncertainty Cabric et al Spurious tones, filter shapes, temperature changes – all impact our knowledge of noise. Calibration can reduce uncertainty but not eliminate it

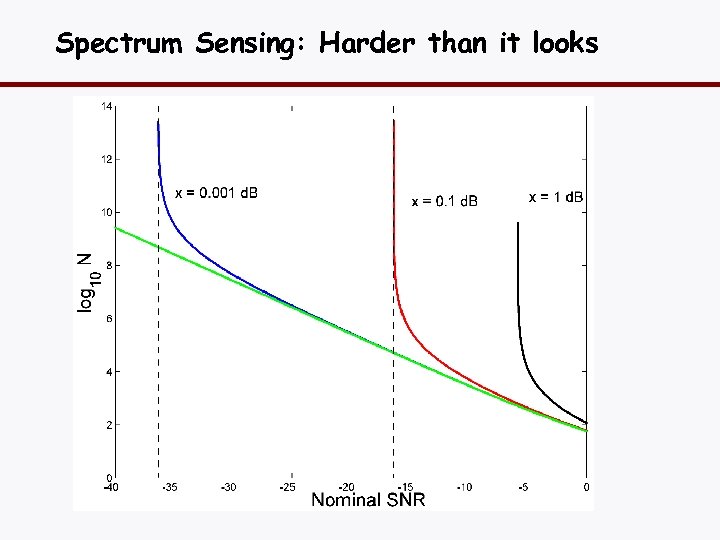Spectrum Sensing: Harder than it looks

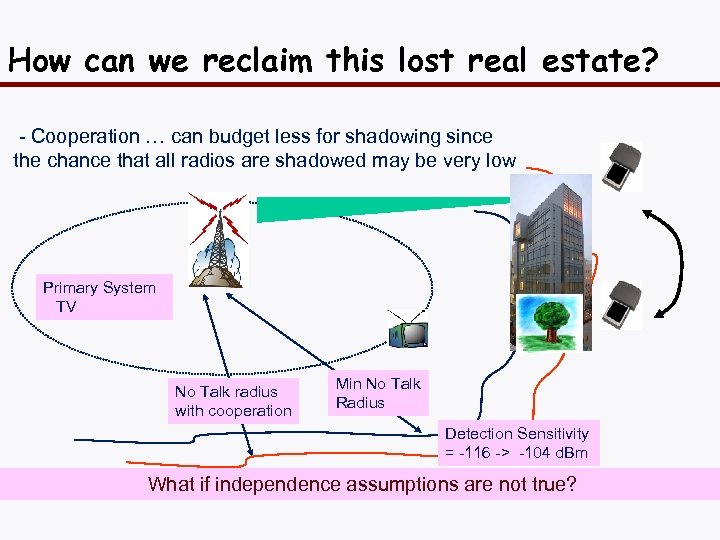How can we reclaim this lost real estate? - Cooperation … can budget less for shadowing since the chance that all radios are shadowed may be very low Primary System TV No Talk radius with cooperation Min No Talk Radius Detection Sensitivity = -116 -> -104 d. Bm What if independence assumptions are not true?

Need right metrics for safety and performance • Safety: no harmful interference to primary • Performance: recovered area for the secondary. • Fundamental incentive incompatibility in models – Secondary is tempted to be optimistic in optimizing performance. – The primary will always be more skeptical of the model.

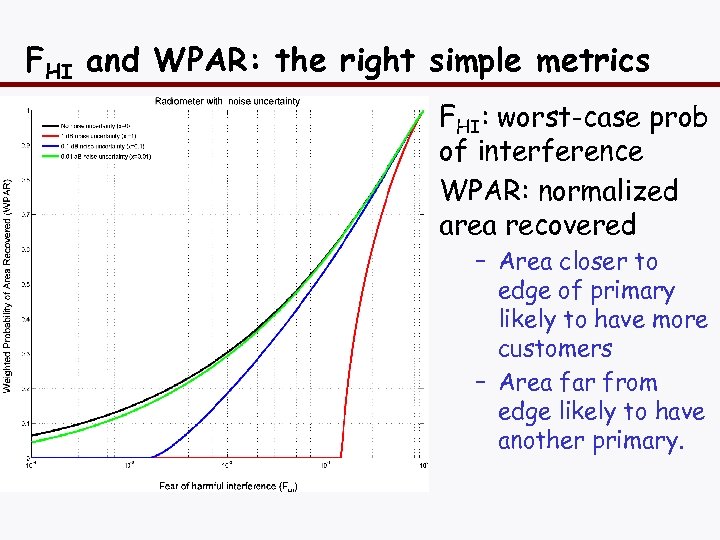FHI and WPAR: the right simple metrics FHI: worst-case prob of interference WPAR: normalized area recovered – Area closer to edge of primary likely to have more customers – Area far from edge likely to have another primary.

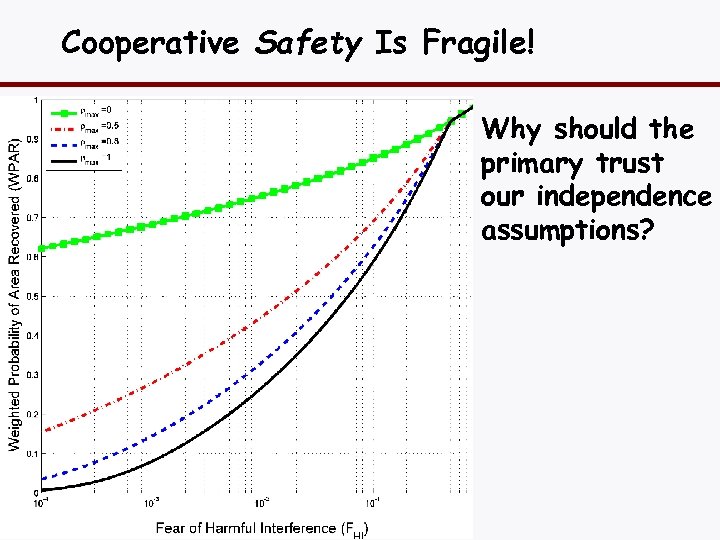Cooperative Safety Is Fragile! Why should the primary trust our independence assumptions?

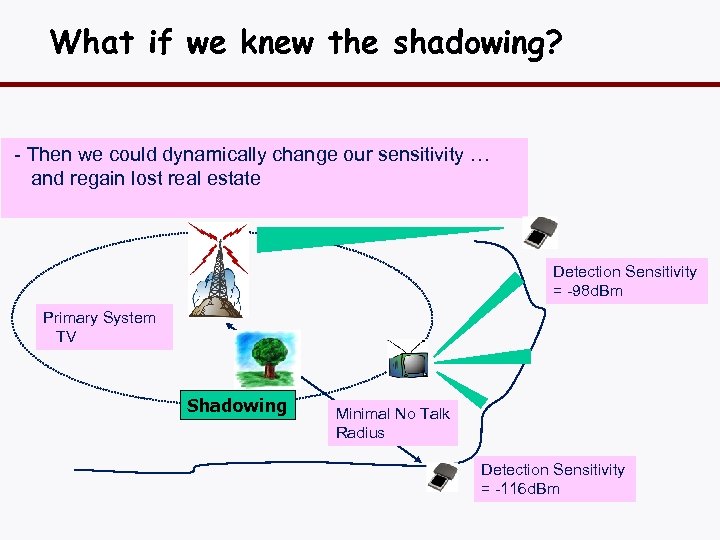What if we knew the shadowing? - Then we could dynamically change our sensitivity … and regain lost real estate Detection Sensitivity = -98 d. Bm Primary System TV Shadowing Minimal No Talk Radius Detection Sensitivity = -116 d. Bm

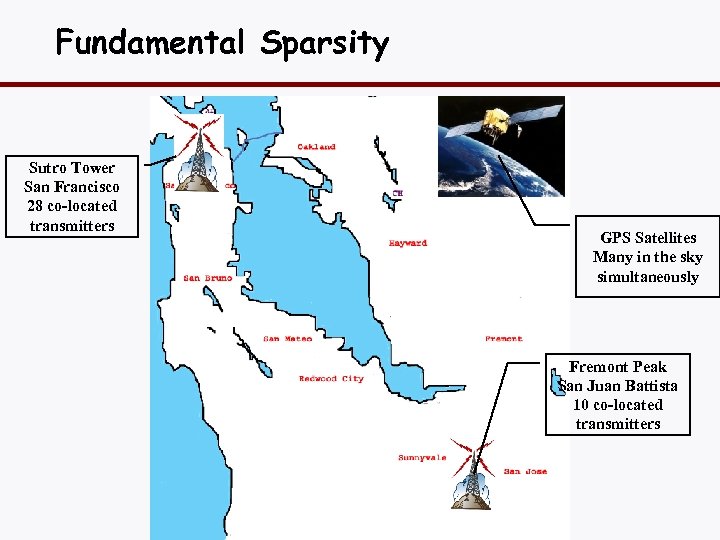Fundamental Sparsity Sutro Tower San Francisco 28 co-located transmitters GPS Satellites Many in the sky simultaneously Fremont Peak San Juan Battista 10 co-located transmitters

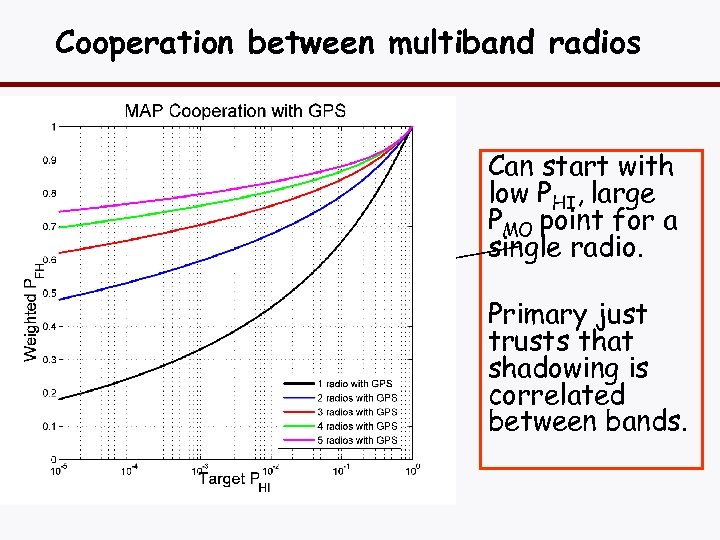Cooperation between multiband radios Can start with low PHI, large PMO point for a single radio. Primary just trusts that shadowing is correlated between bands.

Video and Image Processing Lab • Theories, algorithms and applications of signals; image, video, and 3 D data processing; • Director: Prof. Zakhor; founded in 1988 • Current areas of activities: • Fast, automated, 3 D modeling, visualization and rendering of large scale environments: indoor and outdoor • Wireless multimedia communication • Applications of image processing to IC processing: maskless lithography; optical proximity correction

Figure 1: An example of a residential area in downtown Berkeley which has been texture mapped with 8 airborne pictures on top of 3 D geometry obtained via 1/2 meter resolution airborne lidar data