Combinatorial Scientific Computing Experiences Directions and Challenges John

Combinatorial Scientific Computing: Experiences, Directions, and Challenges John R. Gilbert University of California, Santa Barbara DOE CSCAPES Workshop June 11, 2008 1 Support: DOE Office of Science, DARPA, SGI, MIT Lincoln Labs

Combinatorial Scientific Computing “I observed that most of the coefficients in our matrices were zero; i. e. , the nonzeros were ‘sparse’ in the matrix, and that typically the triangular matrices associated with the forward and back solution provided by Gaussian elimination would remain sparse if pivot elements were chosen with care” - Harry Markowitz, describing the 1950 s work on portfolio theory that won the 1990 Nobel Prize for Economics 2

Combinatorial Scientific Computing “The emphasis on mathematical methods seems to be shifted more towards combinatorics and set theory – and away from the algorithm of differential equations which dominates mathematical physics. ” - John von Neumann & Oskar Morgenstern, 1944 3

Combinatorial Scientific Computing “Combinatorial problems generated by challenges in data mining and related topics are now central to computational science. Finally, there’s the Internet itself, probably the largest graph-theory problem ever confronted. ” - Isabel Beichl & Francis Sullivan, 2008 4

A few directions in CSC • • • 5 Hybrid discrete & continuous computations Multiscale combinatorial computation Analysis, management, and propagation of uncertainty Economic & game-theoretic considerations Computational biology & bioinformatics Computational ecology Knowledge discovery & machine learning Relationship analysis Web search and information retrieval Sparse matrix methods Geometric modeling. . .

Ten Challenges in Combinatorial Scientific Computing 6

#1: The Parallelism Challenge Two Nvidia 8800 GPUs > 1 TFLOPS LANL / IBM Roadrunner > 1 PFLOPS § Different programming models § Different levels of fit to irregular problems & graph algorithms 7 Intel 80 core chip > 1 TFLOPS

#2: The Architecture Challenge Ø The memory wall: Most of memory is hundreds or thousands of cycles away from the processor that wants it. Ø Computations that follow the edges of irregular graphs are unavoidably latency-limited. Ø Speed of light: “You can buy more bandwidth, but you can’t buy less latency. ” Ø Some help from encapsulating coarse-grained primitives in carefully-tuned library routines. . . Ø . . . but the difficulty is intrinsic to most graph computations, hence can likely only be addressed by machine architecture. 8

An architectural approach: Cray MTA / XMT • • Per-tick context switching • Slower clock rate • Uniform (sort of) memory access time • 9 Hide latency by massive multithreading But the economic case is less than completely clear….

#3: The Algorithms Challenge Ø Efficient sequential algorithms for combinatorial problems often follow long sequential dependencies. Ø Example: Assefaw’s talk on graph coloring Ø Several parallelization strategies exist, but no silver bullet: Ø Partitioning (e. g. for coloring) Ø Pointer-jumping (e. g. for connected components) Ø Sometimes it just depends on the graph. . 10

Sample kernel: Sort logically triangular matrix Original matrix Permuted to upper triangular form • • Simple kernel, abstracts many other graph operations (see next) • Sequential: linear time; greedy topological sort; no locality • 11 Used in sparse linear solvers (e. g. Matlab’s) Parallel: very unbalanced; one DAG level per step; possible long sequential dependencies

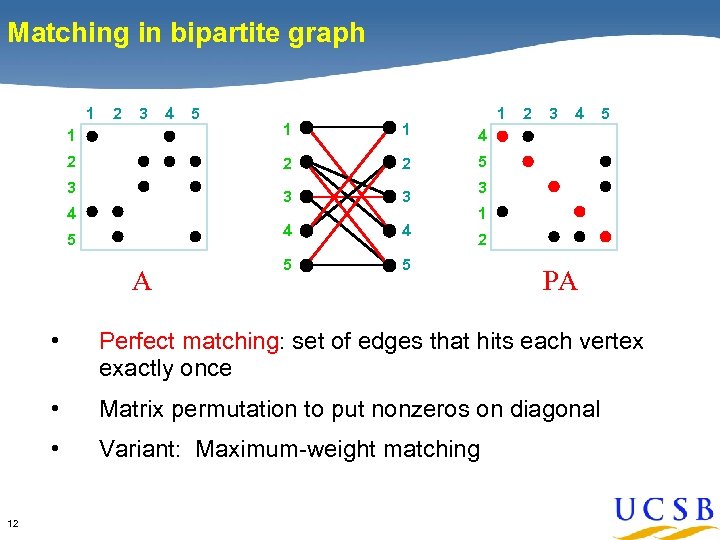
Matching in bipartite graph 1 2 3 4 5 1 1 2 2 3 4 4 5 5 3 3 4 2 2 3 4 5 A 3 1 2 PA • • Matrix permutation to put nonzeros on diagonal • 12 Perfect matching: set of edges that hits each vertex exactly once Variant: Maximum-weight matching

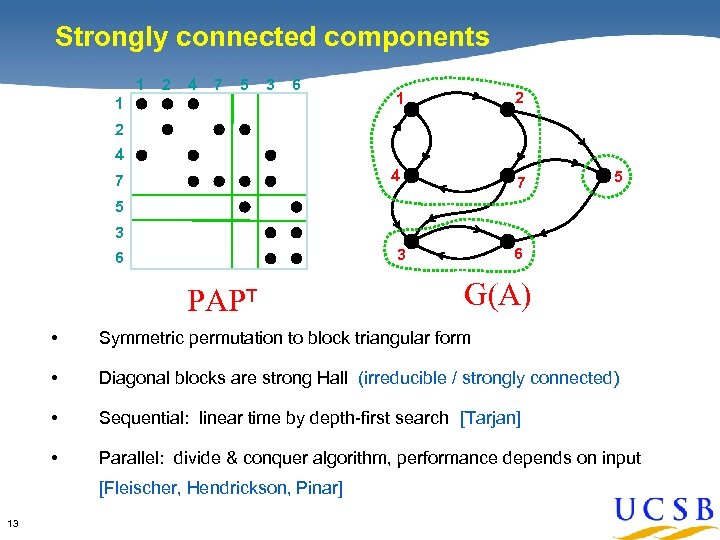
Strongly connected components 1 2 4 7 5 3 6 1 2 4 1 7 2 4 7 5 5 3 6 PAPT G(A) • Symmetric permutation to block triangular form • Diagonal blocks are strong Hall (irreducible / strongly connected) • Sequential: linear time by depth-first search [Tarjan] • Parallel: divide & conquer algorithm, performance depends on input [Fleischer, Hendrickson, Pinar] 13

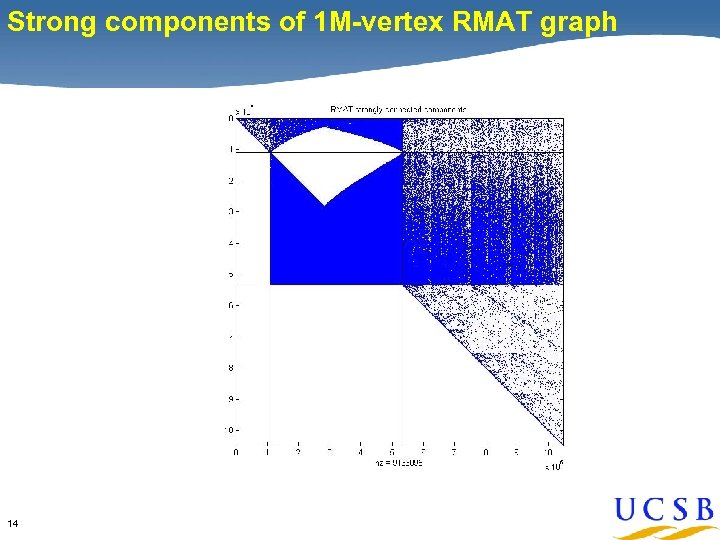
Strong components of 1 M-vertex RMAT graph 14

Coloring for parallel nonsymmetric preconditioning [Aggarwal, Gibou, G] 263 million DOF • • • 15 Level set method for multiphase interface problems in 3 D. Nonsymmetric-structure, second-order-accurate octree discretization. Bi. CGSTAB preconditioned by parallel triangular solves.

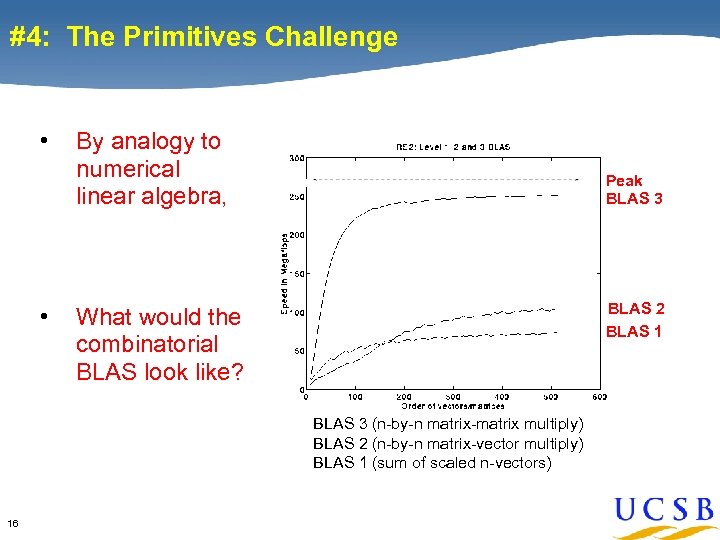
#4: The Primitives Challenge • • By analogy to numerical linear algebra, Peak BLAS 3 BLAS 2 BLAS 1 What would the combinatorial BLAS look like? BLAS 3 (n-by-n matrix-matrix multiply) BLAS 2 (n-by-n matrix-vector multiply) BLAS 1 (sum of scaled n-vectors) 16

Primitives for HPC graph programming • Visitor-based multithreaded – MTGL + XMT + search templates natural for many algorithms + relatively simple load balancing – complex thread interactions, race conditions – unclear how applicable to standard architectures • Array-based data parallel – GAPDT + parallel Matlab / Python + relatively simple control structure + user-friendly interface – some algorithms hard to express naturally – load balancing not so easy • • 17 Scan-based vectorized – NESL: something of a wild card We don’t really know the right set of primitives yet!

Graph algorithms study [Kepner, Fineman, Kahn, Robinson] 18

“Graph Algorithms in the Language of Linear Algebra” • Editors: Kepner (MIT-LL) and Gilbert (UCSB) • Contributors 19 – – – – Bader (GA Tech) Buluc (UCSB) Chakrabarti (CMU) Dunlavy (Sandia) Faloutsos (CMU) Fineman (MIT-LL & MIT) Gilbert (UCSB) Kahn (MIT-LL & Brown) Kegelmeyer (Sandia) Kepner (MIT-LL) Kleinberg (Cornell) Kolda (Sandia) Leskovec (CMU) Madduri (GA Tech) Robinson (MIT-LL & NEU) Shah (ISC & UCSB) Graph Algorithms in the Language of Linear Algebra Jeremy Kepner and John R. Gilbert (editors)

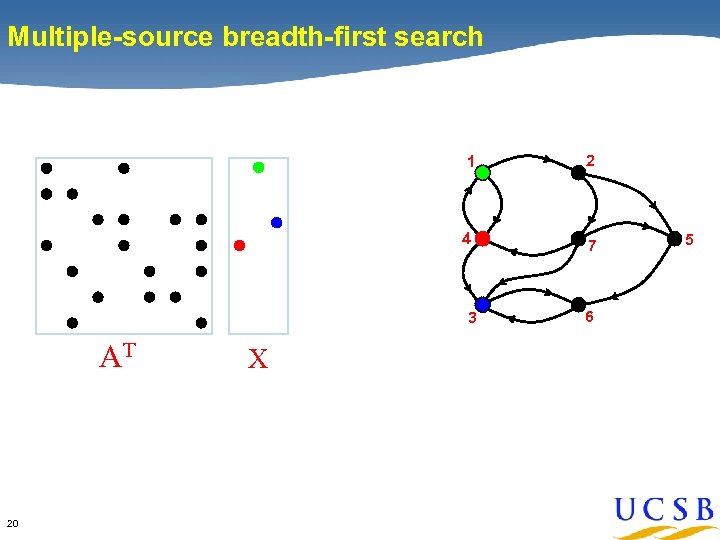
Multiple-source breadth-first search 1 2 4 7 3 AT 20 X 6 5

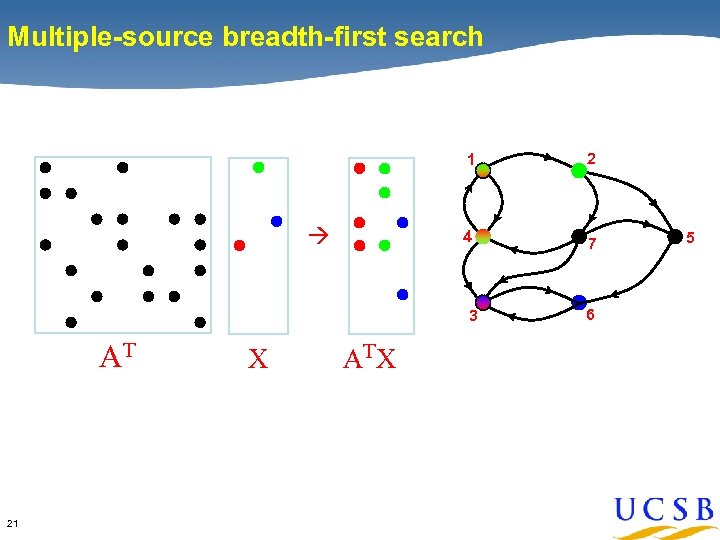
Multiple-source breadth-first search 1 4 2 7 3 AT 21 X AT X 6 5

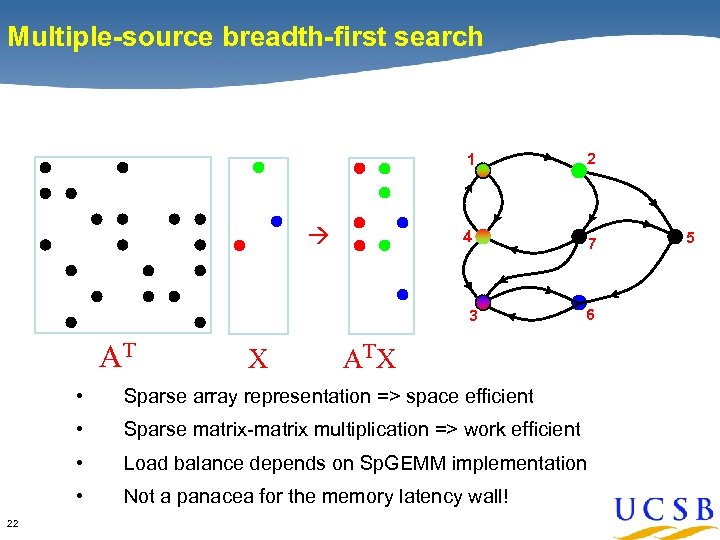
Multiple-source breadth-first search 1 4 2 7 3 AT X 6 AT X • • Sparse matrix-matrix multiplication => work efficient • Load balance depends on Sp. GEMM implementation • 22 Sparse array representation => space efficient Not a panacea for the memory latency wall! 5

Sp. GEMM: Sparse Matrix x Sparse Matrix [Buluc, G] • • Betweenness centrality • BFS from multiple source vertices • Subgraph / submatrix indexing • Graph contraction • Cycle detection • Multigrid interpolation & restriction • Colored intersection searching • Applying constraints in finite element computations • 23 Shortest path calculations (APSP) Context-free parsing

Parallel dense case Parallel Efficiency: p(0, 0) p(0, 1) p(0, 2) p(1, 0) p(1, 1) p(1, 2) p(2, 0) p(2, 1) p(2, 2) 1 -D Layout: 2 -D Layout: • • 24 In the dense case, 2 -D scales better with the number of processors Turns out to be same for the sparse case. . Should be zero for perfect efficiency

Upper bounds on speedup, sparse 1 -D & 2 -D [ICPP’ 08] 2 -D algorithm 1 -D algorithm N P N • 1 -D algorithms do not scale beyond 40 x • Break-even point is around 50 processors. 25 P

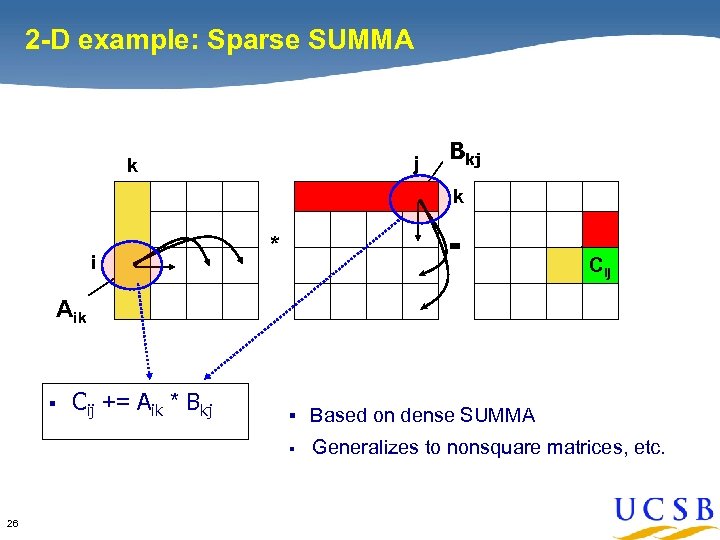
2 -D example: Sparse SUMMA j k Bkj k i * = Cij Aik § Cij += Aik * Bkj § Based on dense SUMMA § 26 Generalizes to nonsquare matrices, etc.

Submatrices are hypersparse (i. e. nnz << n) nnz’ = blocks Average of c nonzeros per column Total Storage: blocks • A data structure or algorithm that depends on the matrix dimension n (e. g. CSR or CSC) is asymptotically too wasteful for submatrices 27

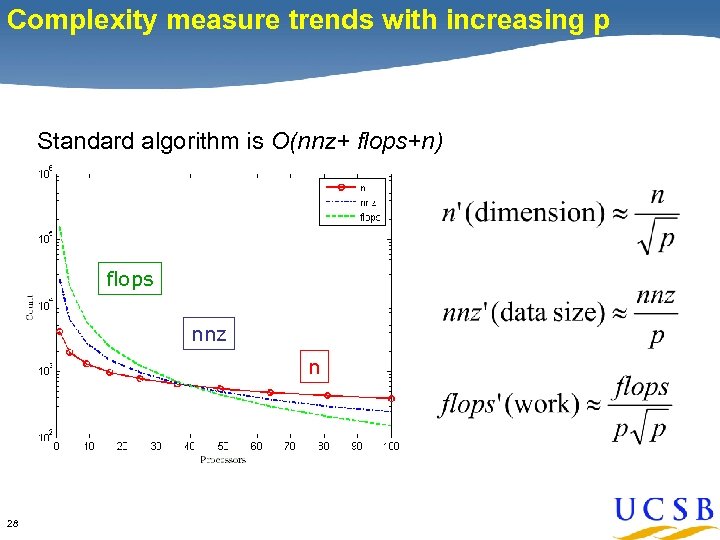
Complexity measure trends with increasing p Standard algorithm is O(nnz+ flops+n) flops nnz n 28

#5: The Libraries Challenge Ø Ø What languages, libraries, and environments will support combinatorial scientific computing? Ø 29 The software version of the primitives challenge! Zoltan, (P)BGL, MTGL, . .

SNAP [Bader & Madduri] 30

GAPDT: Toolbox for graph analysis and pattern discovery [G, Reinhardt, Shah] Layer 1: Graph Theoretic Tools • • Global structure of graphs • Graph partitioning and clustering • Graph generators • Visualization and graphics • Scan and combining operations • 31 Graph operations Utilities

Sample application stack Computational ecology, CFD, data exploration Applications CG, Bi. CGStab, etc. + combinatorial preconditioners (AMG, Vaidya) Preconditioned Iterative Methods Graph querying & manipulation, connectivity, spanning trees, geometric partitioning, nested dissection, NNMF, . . . Graph Analysis & PD Toolbox Arithmetic, matrix multiplication, indexing, solvers (, eigs) Distributed Sparse Matrices 32

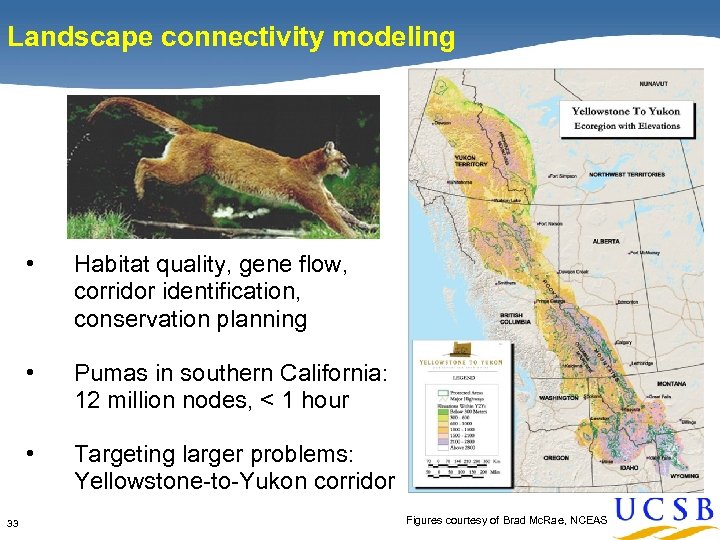
Landscape connectivity modeling • • Pumas in southern California: 12 million nodes, < 1 hour • 33 Habitat quality, gene flow, corridor identification, conservation planning Targeting larger problems: Yellowstone-to-Yukon corridor Figures courtesy of Brad Mc. Rae, NCEAS

#6: The Productivity Challenge “Once we settled down on it, it was sort of like digging the Panama Canal - one shovelful at a time. ” - Ken Appel (& Wolfgang Haken), 1976 34

Productivity Raw performance isn’t always the only criterion. Other factors include: • • Interactive response for exploration and visualization • Rapid prototyping • Usability by non-experts • 35 Seamless scaling from desktop to HPC Just plain programmability

Interactive graph viz [Hollerer & Trethewey] • • Distant vertices stay put, selected vertex moves to place • 36 Nonlinearly-scaled breadth-first search Real-time click&drag for moderately large graphs

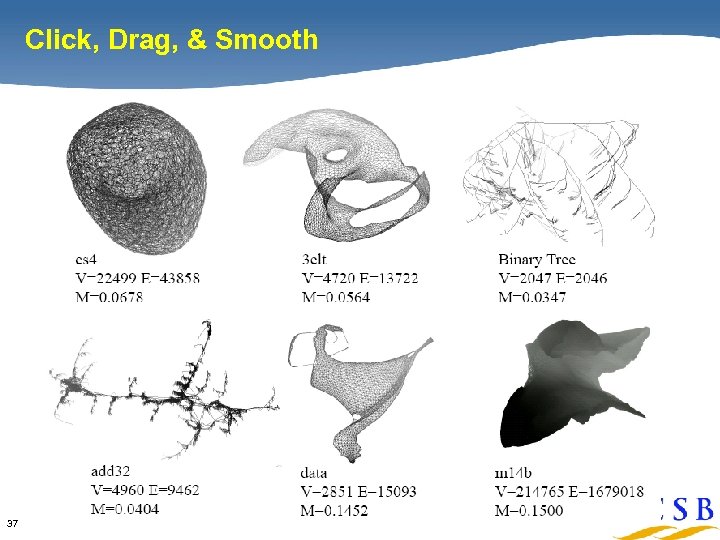
Click, Drag, & Smooth 37

#7: The Data Size Challenge “Can we understand anything interesting about our data when we do not even have time to read all of it? ” - Ronitt Rubinfeld 38

Issues in (many) large graph applications • Where does the graph live? Disk or memory? • Often want approximate answers from sampling • Multiple simultaneous queries to same graph – – • Graph may be fixed, or slowly changing Throughput and response time both important Dynamic subsetting – – 39 User needs to solve problem on “my own” version of the main graph E. g. landscape data masked by geographic location, filtered by obstruction type, resolved by species of interest

Factoring network flow behavior [Karpinski, Almeroth, Belding, G] 40

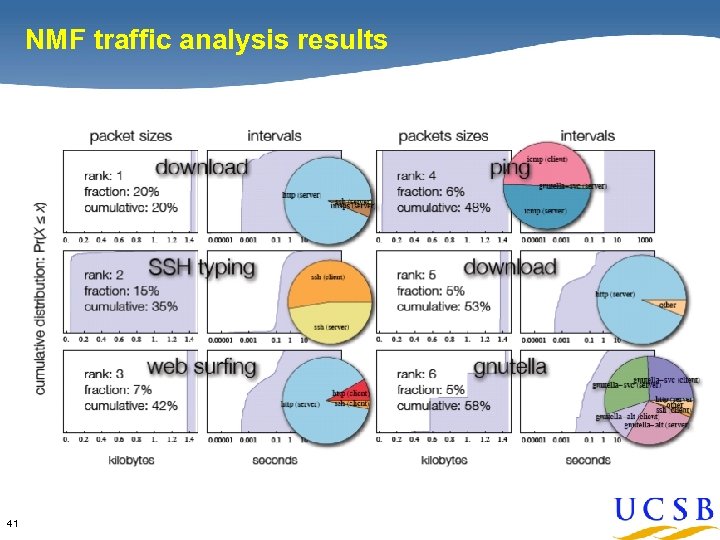
NMF traffic analysis results 41

#8: The Uncertainty Challenge • “Discrete” quantities may be probability distributions • May want to manage and quantify uncertainty between multiple levels of modeling • May want to statistically sample too-large data, or extrapolate probabilistically from incomplete data • For example, in graph algorithms: – – Vertex / edge labels may be stochastic – 42 The graph itself may not be known with certainty May want analysis of sensitivities or thresholds

Horizontal-vertical decomposition of dynamical systems [Mezic et al. ] 43

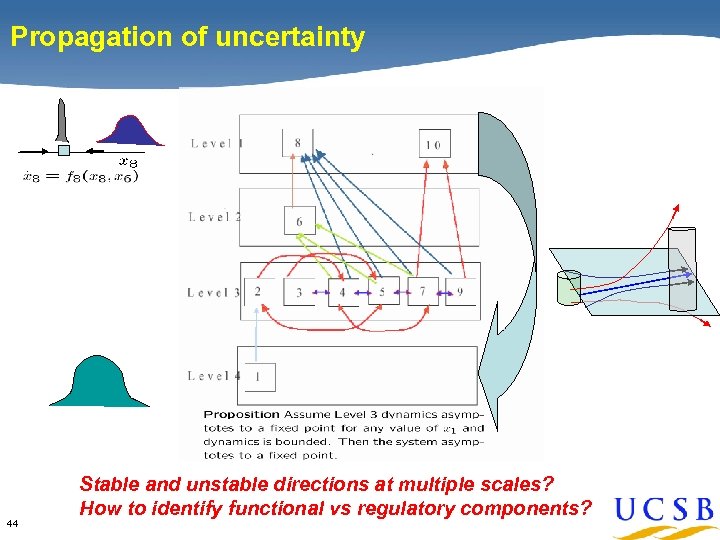
Propagation of uncertainty 44 Stable and unstable directions at multiple scales? How to identify functional vs regulatory components?

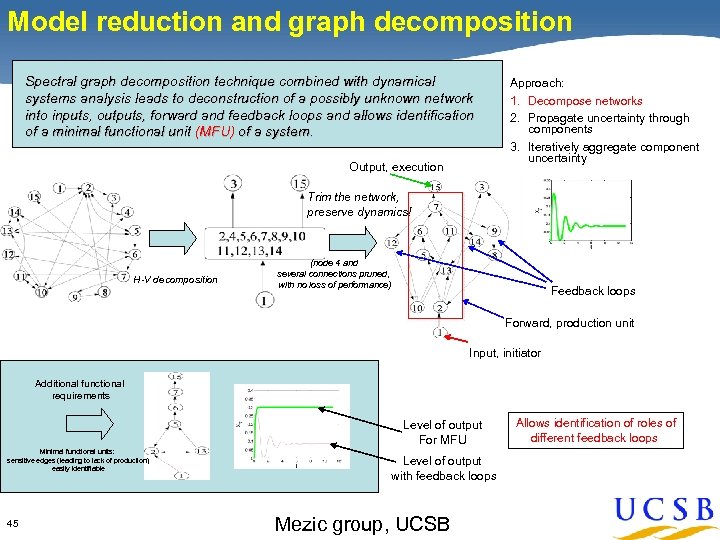
Model reduction and graph decomposition Spectral graph decomposition technique combined with dynamical systems analysis leads to deconstruction of a possibly unknown network into inputs, outputs, forward and feedback loops and allows identification of a minimal functional unit (MFU) of a system. Output, execution Approach: 1. Decompose networks 2. Propagate uncertainty through components 3. Iteratively aggregate component uncertainty Trim the network, preserve dynamics! H-V decomposition (node 4 and several connections pruned, with no loss of performance) Feedback loops Forward, production unit Input, initiator Additional functional requirements Level of output For MFU Minimal functional units: sensitive edges (leading to lack of production) easily identifiable 45 Level of output with feedback loops Mezic group, UCSB Allows identification of roles of different feedback loops

46

Larval connectivity 47

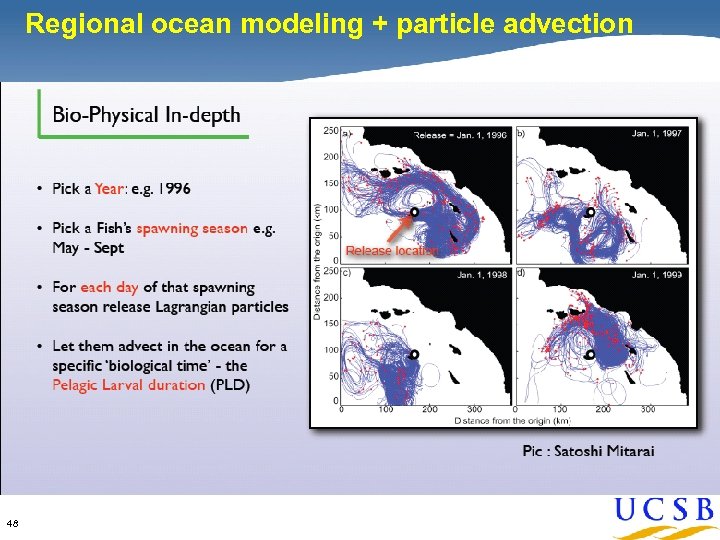
Regional ocean modeling + particle advection 48

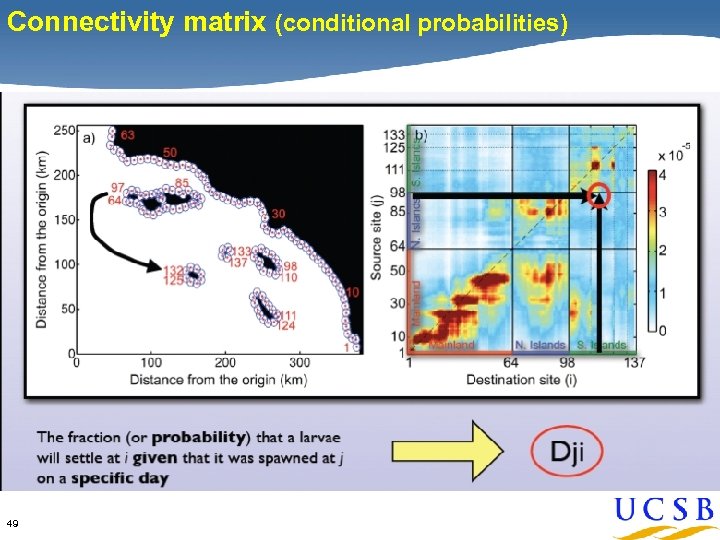
Connectivity matrix (conditional probabilities) 49

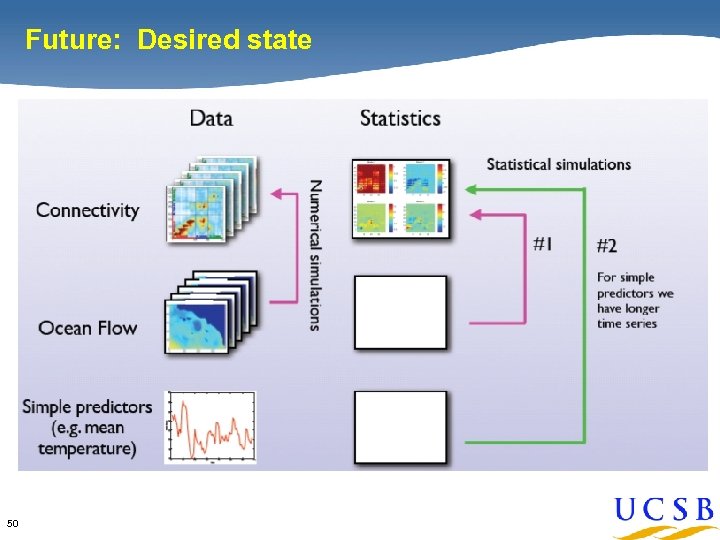
Future: Desired state 50

Parallel modeling of fish interaction [Barbaro, Trethewey, Youssef, Birnir, G] • Capelin schools in seas around Iceland – – • Economic impact and ecological impact Collapse of stock in several prominent fishing areas demonstrates the need for careful tracking of fish Limitations on modeling – – • 51 Group-behavior phenomena missed by lumped models Real schools contain billions of fish; thousands of iterations Challenges include dynamic load balancing and accurate multiscale modeling

#9: The Education Challenge Ø How do you teach this stuff? Ø Where do you go to take courses in Ø Graph algorithms … Ø … on massive data sets … Ø … in the presence of uncertainty … Ø … analyzed on parallel computers … Ø … applied to a domain science? Ø 52 This another whole discussion, but a crucial one.

#10: The Foundations Challenge “Numerical analysis is the study of algorithms for the problems of continuous mathematics. ” - L. Nick Trefethen 53

CS and CS&E (Hendrickson 2003) Computer Science Algorithmics l. What’s Computational Science in the intersection? » Combinatorial Scientific Computing 54

NIST workshop 2007: “Foundations of Measurement Science for Information Systems” A few suggested research areas in measurement science for complex networks: Ø Measurement of global properties of networks: – Not just density, diameter, degree distribution, etc. – Connectivity, robustness – Spectral properties: Laplacian eigenvectors, Cheeger bounds, … – Other global measures of complexity? – Sensitivity analysis of all of the above – Stochastic settings for all of the above Ø Ø Building useful reference data sets and generators Ø 55 Multiscale modeling of complex networks Fundamentals of high-performance combinatorial computing

Ten Challenges In CSC 1. Parallelism 2. Architecture 7. Data size 3. Algorithms 8. Uncertainty 4. Primitives 9. Education 5. Libraries 56 6. Productivity 10. Foundations

Morals (from Hendrickson, 2003) • Things are clearer if you look at them from multiple perspectives • Combinatorial algorithms are pervasive in scientific computing and will become more so • Lots of exciting opportunities – – 57 High impact for discrete algorithms work Enabling for scientific computing

Conclusion This is a great time to be doing research in combinatorial scientific computing! 58

Thanks … Vikram Aggarwal, David Bader, Alethea Barbaro, Jon Berry, Aydin Buluc, Alan Edelman, Jeremy Fineman, Frederic Gibou, Bruce Hendrickson, Tobias Hollerer, Crystal Kahn, Stefan Karpinski, Jeremy Kepner, Jure Leskovic, Brad Mc. Rae, Igor Mezic, Cleve Moler, Steve Reinhardt, Eric Robinson, Rob Schreiber, Viral Shah, Peterson Trethewey, James Watson, Lamia Youssef 59