Combinatorial auctions in theory and practice Graham Louth

Combinatorial auctions in theory and practice Graham Louth, Director of Spectrum Policy 11 March 2010 ©Ofcom 0

Ofcom • The UK’s communications regulator with responsibilities across: – TV and radio broadcasting – fixed and mobile networks and services – management of the electro-magnetic spectrum (for wireless communications and other purposes) ©Ofcom 1

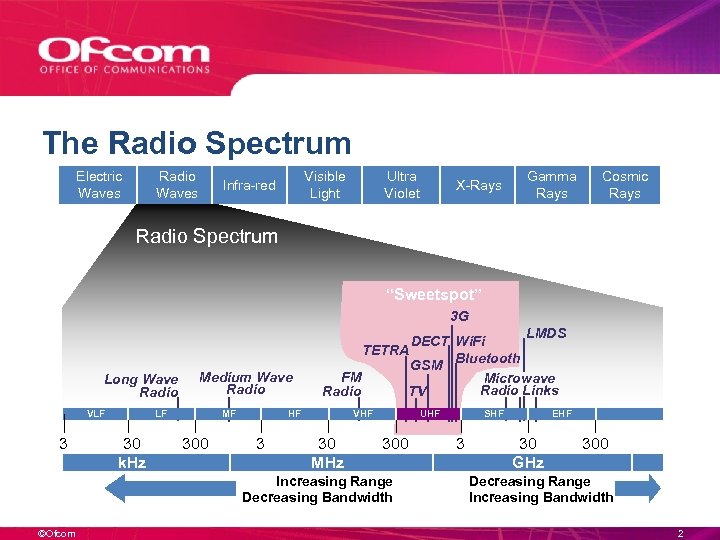
The Radio Spectrum Electric Waves Radio Waves Visible Light Infra-red Ultra Violet X-Rays Gamma Rays Cosmic Rays Radio Spectrum “Sweetspot” 3 G Long Wave Radio VLF 3 Medium Wave Radio LF 30 k. Hz MF 300 LMDS DECT Wi. Fi TETRA Bluetooth GSM FM Microwave Radio Links Radio TV HF 3 VHF 30 MHz UHF 300 Increasing Range Decreasing Bandwidth ©Ofcom SHF 3 EHF 30 GHz 300 Decreasing Range Increasing Bandwidth 2

Ofcom’s statutory duties • 3(1)(a) Further the interests of citizens in relation to • communications matters 3(1)(b) Further the interests of consumers in relevant markets, where appropriate by promoting competition • 3(2)(a) Secure the optimal use for wireless telegraphy • • of the electro-magnetic spectrum 3(4)(d) Have regard for the desirability of encouraging investment and innovation in relevant markets 3(4)(f) Have regard for the different needs and interests of all persons who may wish to make use of the spectrum ©Ofcom 3

Why auctions? • Need to choose between conflicting demands for limited amount of • • • spectrum Want a mechanism that is fair, transparent and robust Want to avoid pre-judging what constitutes ‘best use’ Want to minimise constraints on future use • NOT to raise revenue – that is just a by-product of the process • Whilst not perfect, experience suggests that well designed auctions are generally better at achieving our objectives than alternative award approaches (e. g. beauty contests) ©Ofcom 4

Why combinatorial auctions? • We want to facilitate competition, so want to divide up the available spectrum • into a number of lots We want to allow bidders the flexibility to win the amount and configuration of spectrum that best suits their needs, so we want the lots to be no larger than necessary and to allow bidders to bid for combinations of lots of their choosing (each bid winning or losing as a unit, with the bidder facing no risk of winning only part of what they need) – recognise possibility of (strong) complementarity between lots – lots worth (significantly) more in combination than the sum of their individual values • (Alternative is to allow bidders to simultaneously but separately bid on a number of different lots – puts risks on bidders to manage their exposure, which may lead them to bidding cautiously and consequently lead to an inefficient outcome) ©Ofcom 5

Challenges of combinatorial auctions - 1 • If demand is ‘lumpy’ (strong complementarities) the combination of bidders who are individually willing to pay the highest prices may not constitute the optimal allocation of the spectrum since a different combination of bidders might, in aggregate, be willing to pay more (because they would take up more of the available spectrum): – Need to give bidders the opportunity and incentive to reveal their maximum willingness to pay across a wide range of packages of interest – Need to solve the “winner determination problem” – identify the package of bids which maximises total value subject to accepting at most one bid from each bidder and being able to fit all of the winning bids into the available spectrum (a potentially hard integer programming problem) ©Ofcom 6

Challenges of combinatorial auctions - 2 • There may be a very large number of different combinations of lots of potential interest to bidders; How can they identify those that are most likely to win? – Use a multi-round process so that bidders can see how demand changes as prices increase, and can estimate what final prices are likely to be – Give bidders incentives to reflect their demand truthfully in their bids, so that other bidders can rely upon the demand information that is revealed through earlier rounds ©Ofcom 7

An example – the 10 -40 GHz award Band Total bandwidth available Number of lots offered Bandwidth per lot 10 GHz national 2 x 100 MHz 10 2 x 10 MHz 28 GHz national 2 x 224 MHz 2 2 x 112 MHz 32 GHz national 2 x 756 MHz 6 2 x 126 MHz 40 GHz national 2 x 1500 MHz 6 2 x 250 MHz 28 GHz sub-national 1 2 x 112 MHz 28 GHz sub-national 2 2 x 112 MHz 1 2 x 112 MHz 28 GHz sub-national 3 2 x 112 MHz 1 2 x 112 MHz ©Ofcom 8

Combinatorial clock auction • Auctioneer announces prices – Bidders bid for the quantity they would most like to buy at those prices • Auctioneer looks at total demand increases price where demand exceeds • supply – Bidders respond with new bids, expressing the new quantity that they would most like to buy at those new prices – generally required to be no more in total than the quantity bid for in the previous round, but free to switch demand between different types of lot at will Process continues until demand no longer exceeds supply ©Ofcom 9

10 -40 GHz auction – actual results ©Ofcom 10

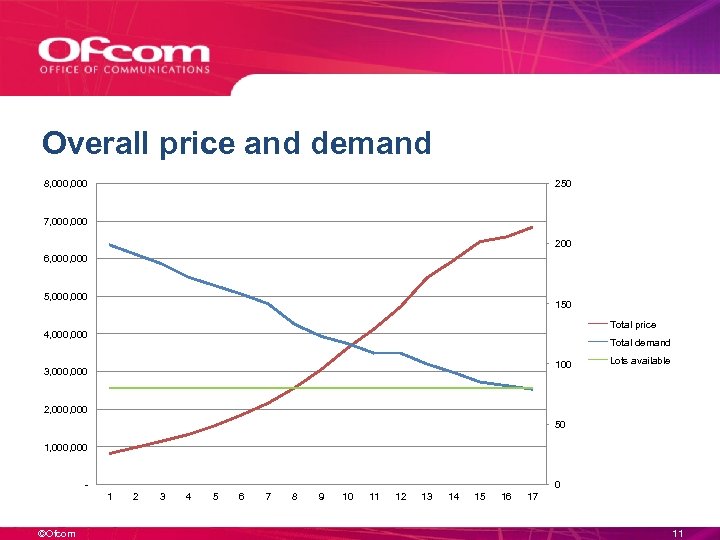
Overall price and demand 8, 000 250 7, 000 200 6, 000 5, 000 150 Total price 4, 000 Total demand 100 3, 000 Lots available 2, 000 50 1, 000 - 0 1 ©Ofcom 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 11

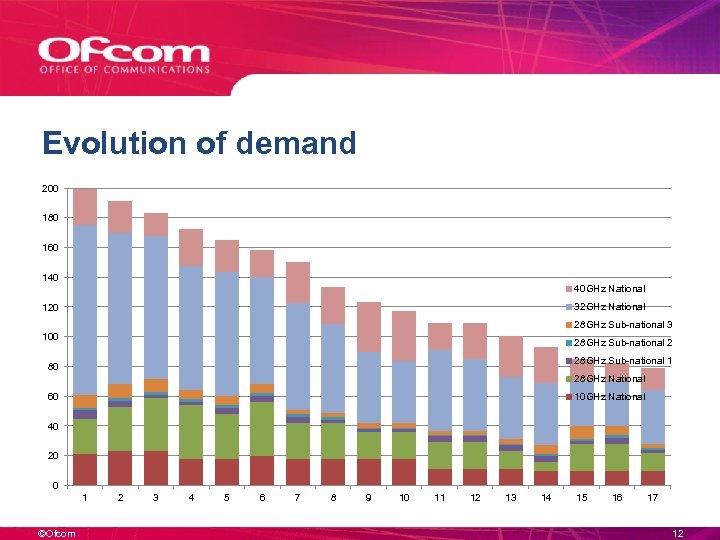
Evolution of demand 200 180 160 140 40 GHz National 32 GHz National 120 28 GHz Sub-national 3 100 28 GHz Sub-national 2 28 GHz Sub-national 1 80 28 GHz National 60 10 GHz National 40 20 0 1 ©Ofcom 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 12

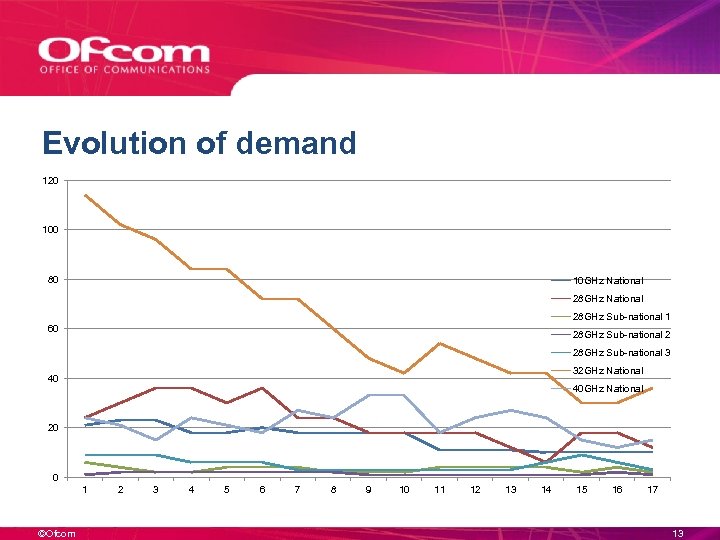
Evolution of demand 120 100 80 10 GHz National 28 GHz Sub-national 1 60 28 GHz Sub-national 2 28 GHz Sub-national 3 32 GHz National 40 40 GHz National 20 0 1 ©Ofcom 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 13

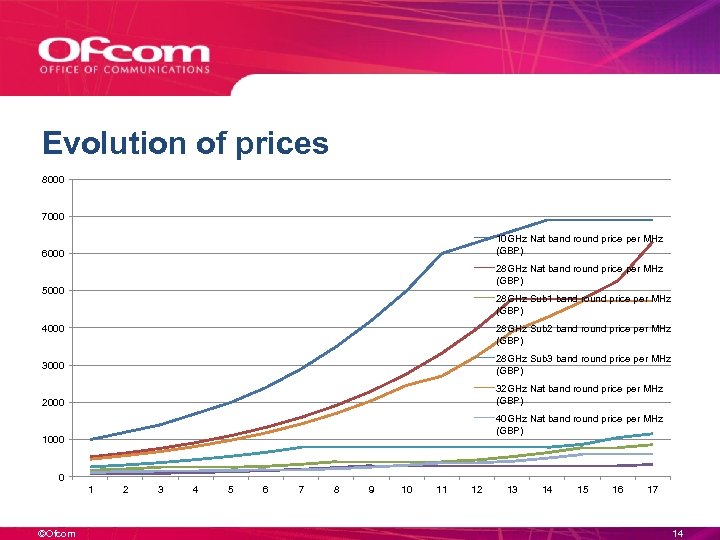
Evolution of prices 8000 7000 10 GHz Nat band round price per MHz (GBP) 6000 28 GHz Nat band round price per MHz (GBP) 5000 28 GHz Sub 1 band round price per MHz (GBP) 4000 28 GHz Sub 2 band round price per MHz (GBP) 3000 28 GHz Sub 3 band round price per MHz (GBP) 2000 32 GHz Nat band round price per MHz (GBP) 40 GHz Nat band round price per MHz (GBP) 1000 0 1 ©Ofcom 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 14

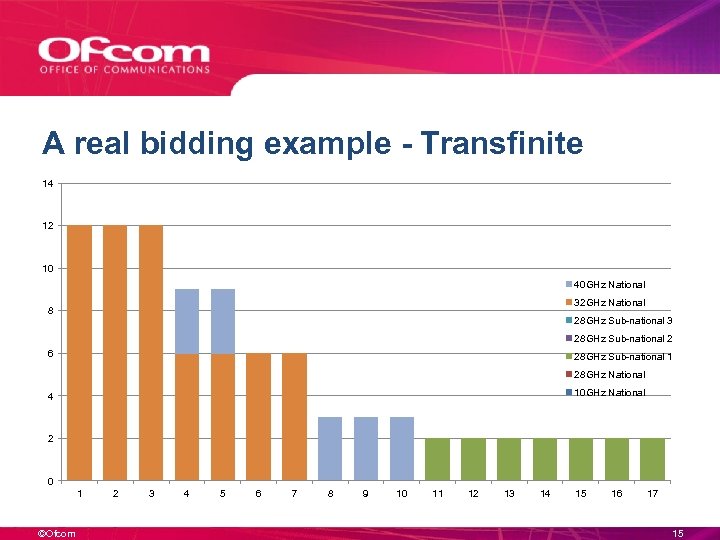
A real bidding example - Transfinite 14 12 10 40 GHz National 32 GHz National 8 28 GHz Sub-national 3 28 GHz Sub-national 2 6 28 GHz Sub-national 1 28 GHz National 10 GHz National 4 2 0 1 ©Ofcom 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 15

Need for supplementary bids • If bidders interested in particular combinations of lots, rather than just more or less of the same thing, result at end of combinatorial clock stage may not be optimal – there may no longer be demand for some of the available spectrum • Need to give bidders the opportunity to express full range of their demand e. g. bid for combinations of lots that they didn’t bid on in the combinatorial clock stage – supplementary bids • Auctioneer then needs to work out which combination of bids generates greatest value – the winner determination problem – (a potentially hard integer programming problem) ©Ofcom 16

Second price rule • In almost all simple multi-round ascending auctions, the auction stops as soon • • as the last losing bidder drops out; the winning bidder(s) then have to pay an amount equal to (or one bid increment greater than) the highest amount that any losing bidder was willing to pay: this is the key characteristic of a second price rule The same idea can be applied in sealed bid auctions (e. g. this is how bidding works on e-Bay), and has the benefit of reducing the incentive for bidders to ‘shade’ their bid – bid less than their true value in order to avoid paying more than necessary – which can lead to inefficient outcomes Second price rules can also be applied in combinatorial auctions, but require the auctioneer (but not bidders) to perform a complex set of calculations; objectives is to give bidders strong incentive to bid the true value to them of the lots they are bidding for: risk of paying more than true value if over-bid; risk of not winning when could have done if under-bid; little chance of reducing amount required to pay by reducing bid ©Ofcom 17

Second price rule – further details • True second price rule in case of combinatorial auction is Vickrey-Clarke. Groves (opportunity cost) pricing • But there a number of serious problems with this pricing rule, not least that VCG prices may not be in the core: – A different coalition of bidders may have offered to pay more in total for the same spectrum – liable to challenge outcome! • We currently use a pricing rule that uses the set of prices in the core that are closest to VCG prices – (an even harder non-linear optimisation problem) – No particularly strong theoretical justification for this rule – but seems to work – Means that in some circumstances winning bidders might be able to reduce their payments (individually, but not collectively) by under-bidding, but likely to be very difficult for a prospective winning bidder to predict this possibility, and doing so creates risk of losing when otherwise would have won ©Ofcom 18

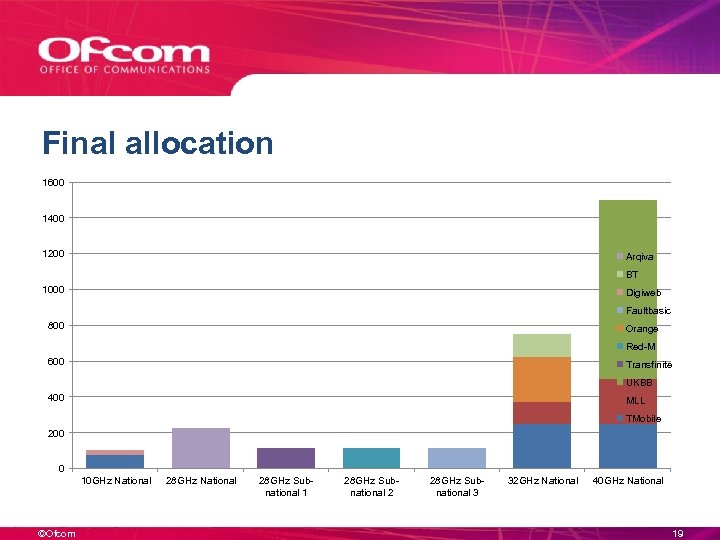
Final allocation 1600 1400 1200 Arqiva BT 1000 Digiweb Faultbasic 800 Orange Red-M 600 Transfinite UKBB 400 MLL TMobile 200 0 10 GHz National ©Ofcom 28 GHz National 28 GHz Subnational 1 28 GHz Subnational 2 28 GHz Subnational 3 32 GHz National 40 GHz National 19

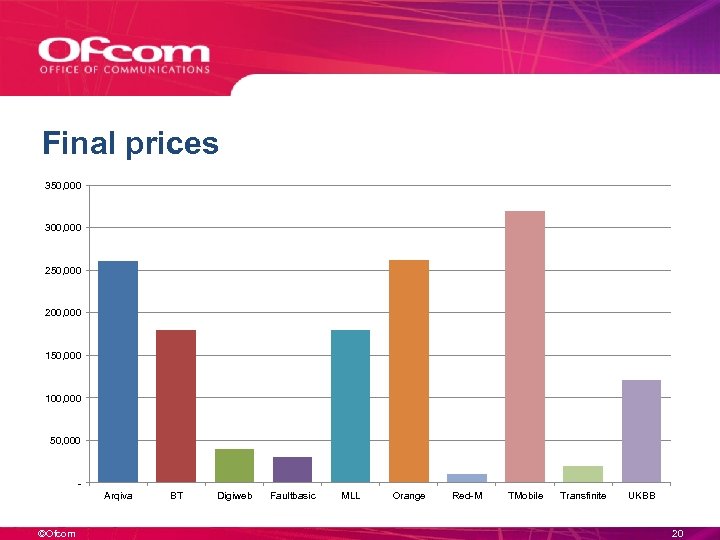
Final prices 350, 000 300, 000 250, 000 200, 000 150, 000 100, 000 50, 000 Arqiva ©Ofcom BT Digiweb Faultbasic MLL Orange Red-M TMobile Transfinite UKBB 20

Current challenges • Winner determination and pricing in a combined buy/sell auction with relative price constraints (!) • Incentive impacts of different variants of core pricing: VCG-closest vs Reference price rules • Auction designs for efficient allocation when bidders have budget constraints ©Ofcom 21

Graham Louth Director of Spectrum Policy graham. louth@ofcom. org. uk www. ofcom. org. uk/radiocomms/spectrumawards ©Ofcom 22