6be19a4c92e4974e345147f4d7c7d6be.ppt
- Количество слайдов: 87

Combinatorial Algorithms for Market Equilibria Vijay V. Vazirani

n Arrow-Debreu Theorem: Equilibria exist.

n Arrow-Debreu Theorem: Equilibria exist. n Do markets operate at equilibria?

n Arrow-Debreu Theorem: Equilibria exist. n Do markets operate at equilibria? n Can equilibria be computed efficiently?

Arrow-Debreu is highly non-constructive

Arrow-Debreu is highly non-constructive n “Invisible hand” of the market: Adam Smith n Scarf, 1973: approximate fixed point algs. n Convex programs: ¨ Fisher: Eisenberg & Gale, 1957 ¨ Arrow-Debreu: Newman and Primak, 1992

n Used for deciding tax policies, price of new products etc. n New markets on the Internet

Algorithmic Game Theory n Use powerful techniques from modern algorithmic theory and notions from game theory to address issues raised by Internet. n Combinatorial algorithms for finding market equilibria.

Two Fundamental Models n Fisher’s model n Arrow-Debreu model, also known as exchange model

Combinatorial Algorithms n Primal-dual schema based algorithms ¨ n Devanur, Papadimitriou, Saberi & V. , 2002 Combinatorial algorithm for Fisher’s model Auction-based algorithms ¨ Garg & Kapoor, 2004 Approximation algorithms.

Approximation n Find prices s. t. all goods clear n Each buyer get goods providing at least optimal utility.

Primal-Dual Schema n Highly successful algorithm design technique from exact and approximation algorithms

Exact Algorithms for Cornerstone Problems in P: n n n Matching (general graph) Network flow Shortest paths Minimum spanning tree Minimum branching

Approximation Algorithms set cover Steiner tree Steiner network k-MST scheduling. . . facility location k-median multicut feedback vertex set

Main new idea n Previous: problems captured via linear programs n DPSV algorithm: problem captured via a nonlinear convex program

Fisher’s Model n n n buyers, with specified money, m(i) for buyer i k goods (unit amount of each good) Linear utilities: is utility derived by i on obtaining one unit of j Total utility of i,

Fisher’s Model n n buyers, with specified money, m(i) k goods (each unit amount, w. l. o. g. ) Linear utilities: is utility derived by i on obtaining one unit of j Total utility of i, n Find prices s. t. market clears n n n
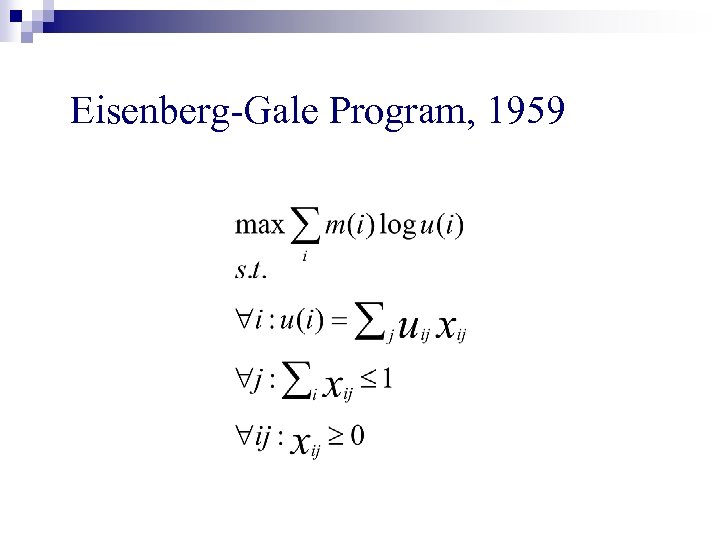
Eisenberg-Gale Program, 1959

DPSV Algorithm n “primal” variables: allocations of goods n “dual” variables: prices n algorithm: primal & dual improvements Allocations Prices

Market Equilibrium § Buyer i’s optimization program: § Global Constraint:
People $100 $60 $20 $140 Goods
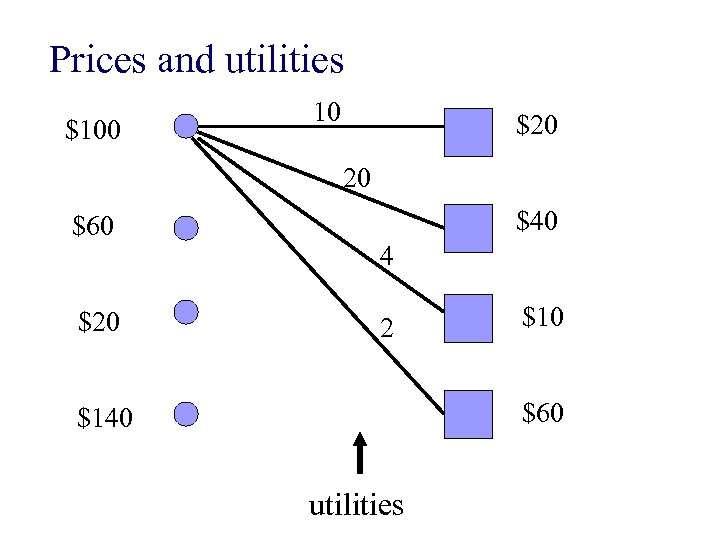
Prices and utilities $100 10 $20 20 $60 $20 $40 4 2 $10 $60 $140 utilities
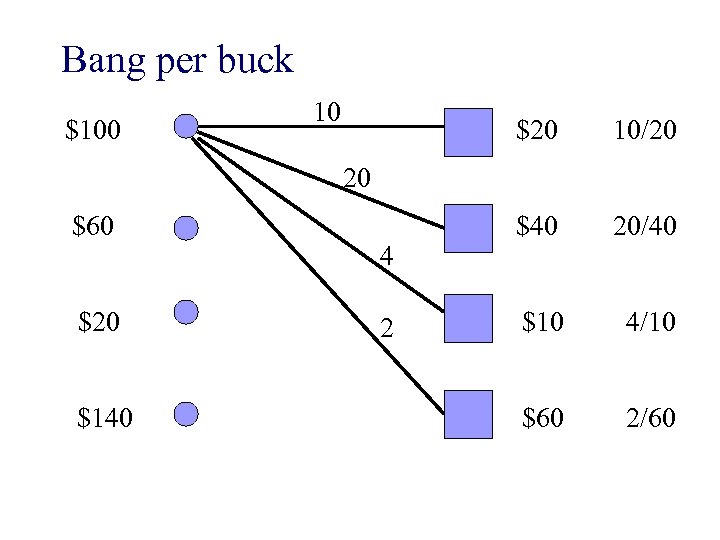
Bang per buck $100 10 $20 10/20 $40 20/40 $10 4/10 $60 2/60 20 $60 $20 $140 4 2

Bang per buck n Utility of $1 worth of goods n Buyers will only buy goods providing maximum bang per buck
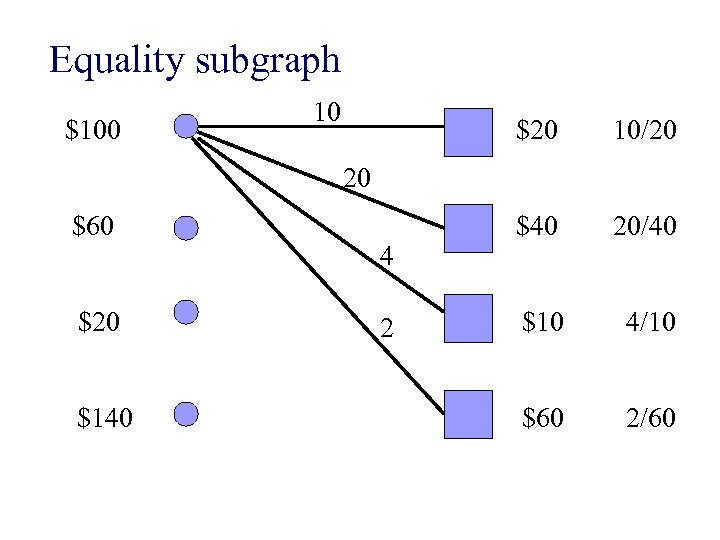
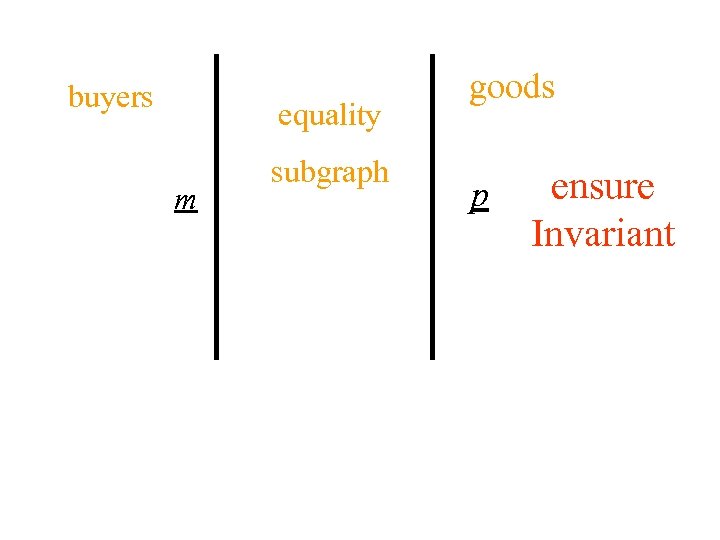
Equality subgraph $100 10 $20 10/20 $40 20/40 $10 4/10 $60 2/60 20 $60 $20 $140 4 2
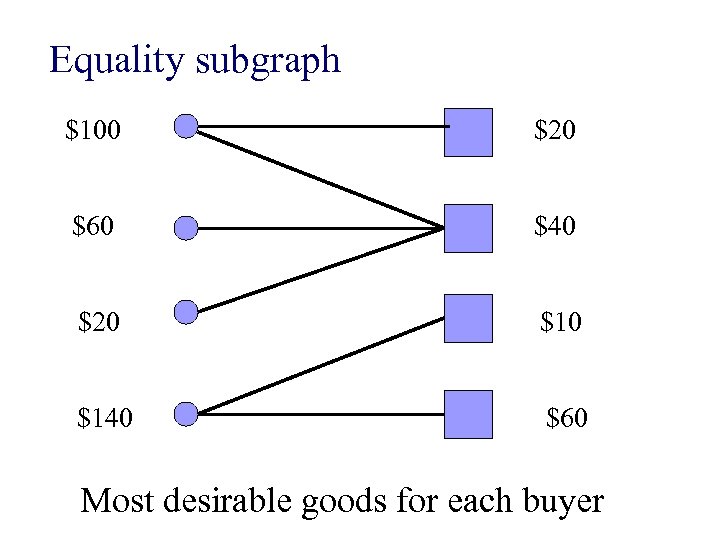
Equality subgraph $100 $20 $60 $40 $20 $140 $60 Most desirable goods for each buyer

n Any goods sold in equality subgraph make agents happiest n How do we maximize sales in equality subgraph?

n Any goods sold in equality subgraph make agents happiest n How do we maximize sales in equality subgraph? Use max-flow!
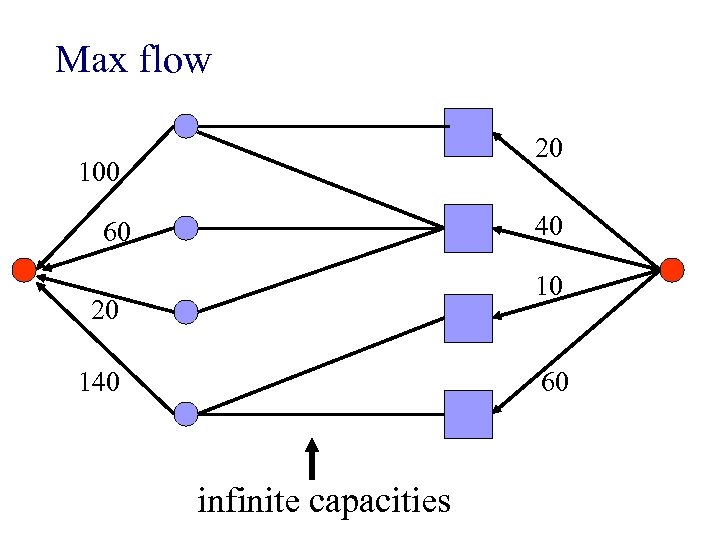
Max flow 20 100 40 60 10 20 140 60 infinite capacities

Idea of Algorithm n Invariant: source edges form min-cut (agents have surplus) n Iterations: gradually raise prices, decrease surplus n Terminate: when surplus = 0, i. e. , sink edges also form a min-cut

Ensuring Invariant initially n Set each price to 1/n n Assume buyers’ money integral

How to raise prices? j i l n Ensure equality edges retained
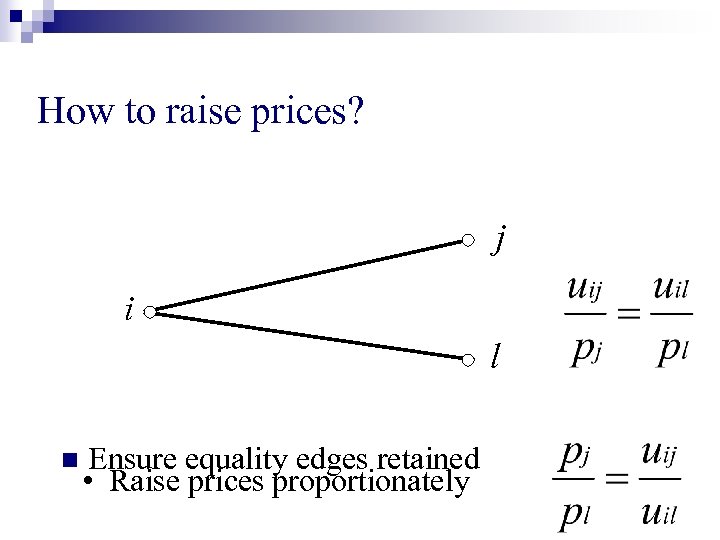
How to raise prices? j i l n Ensure equality edges retained • Raise prices proportionately
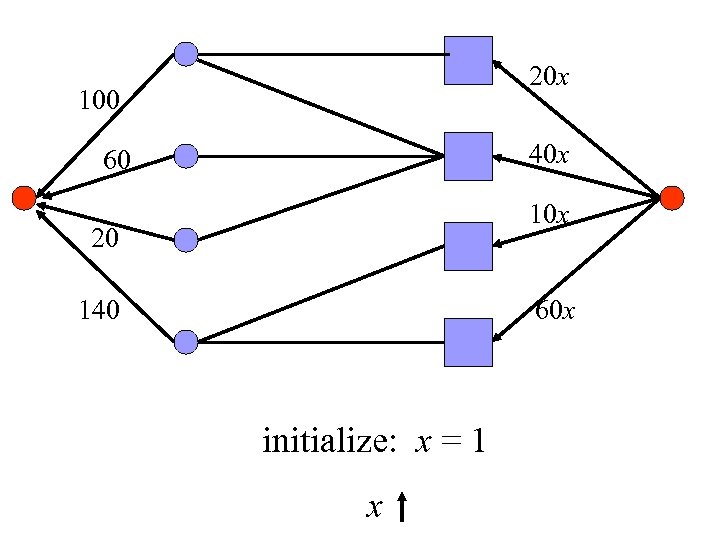
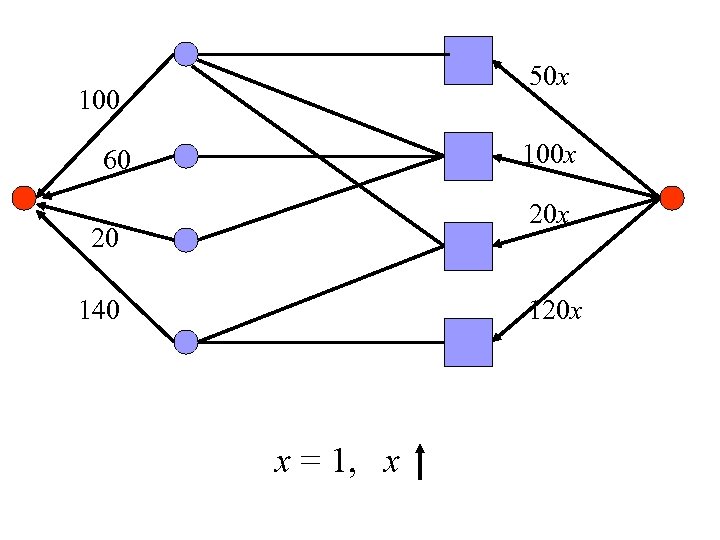
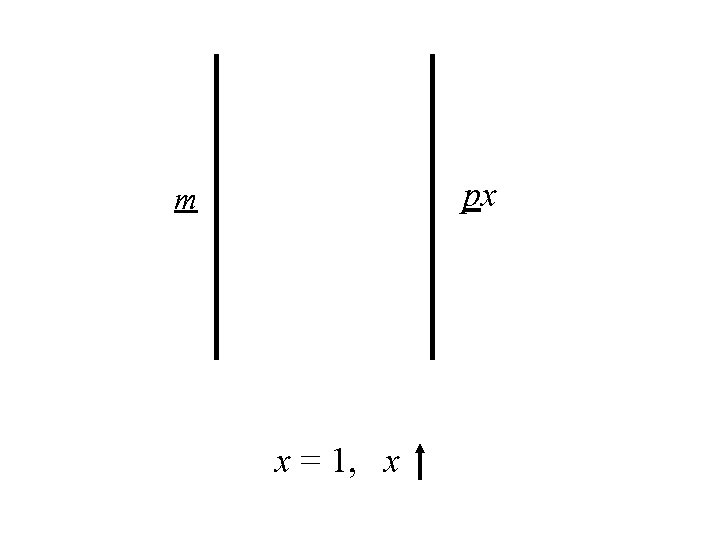
20 x 100 40 x 60 10 x 20 140 60 x initialize: x = 1 x
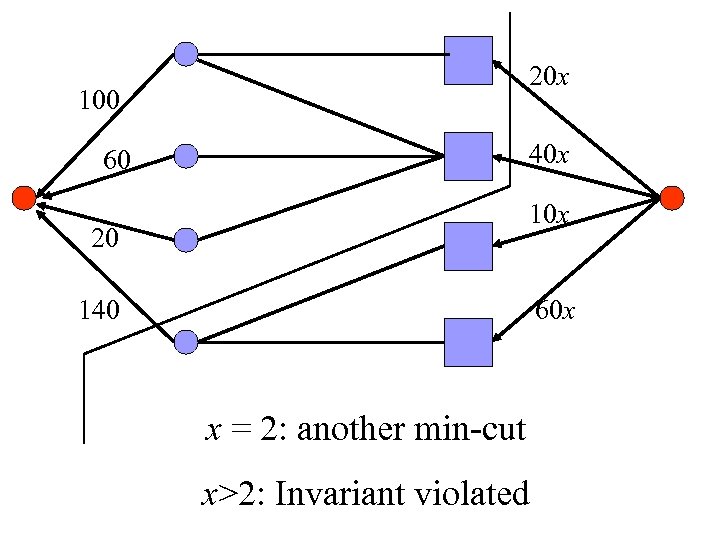
20 x 100 40 x 60 10 x 20 140 60 x x = 2: another min-cut x>2: Invariant violated
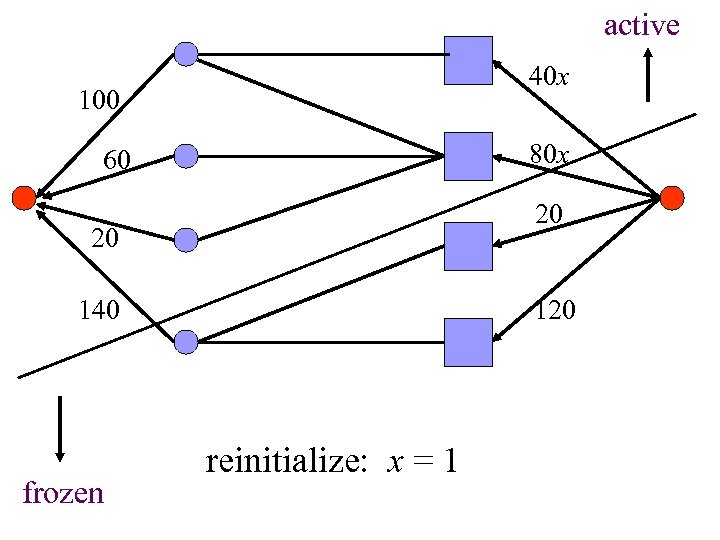
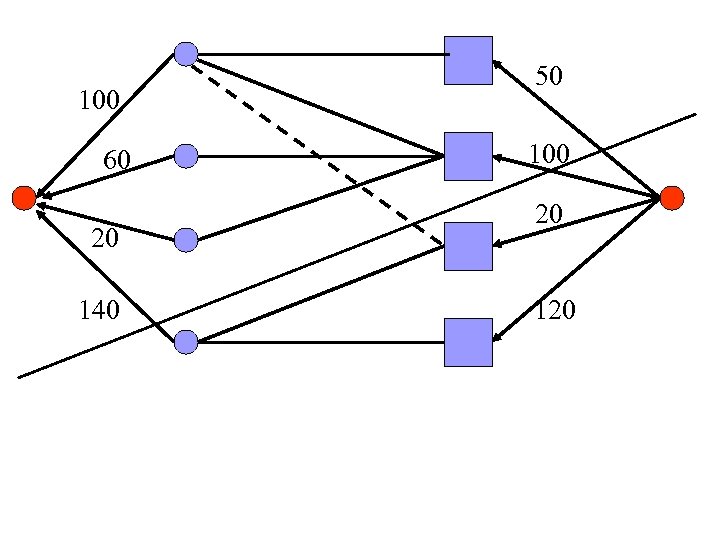
active 40 x 100 80 x 60 20 20 140 frozen 120 reinitialize: x = 1
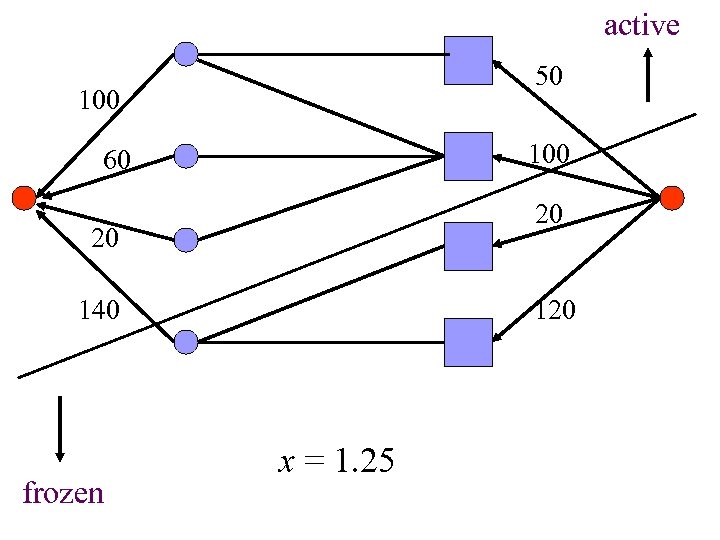
active 50 100 60 20 20 140 frozen 120 x = 1. 25
100 60 20 140 50 100 20 120
100 60 20 140 unfreeze 50 100 20 120
50 x 100 x 60 20 x 20 140 120 x x = 1, x
goods buyers m
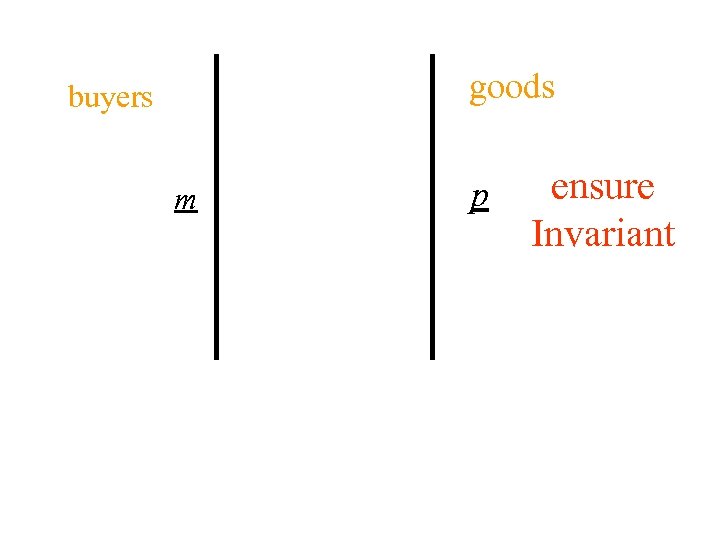
goods buyers m p ensure Invariant
buyers equality m subgraph goods p ensure Invariant
px m x = 1, x
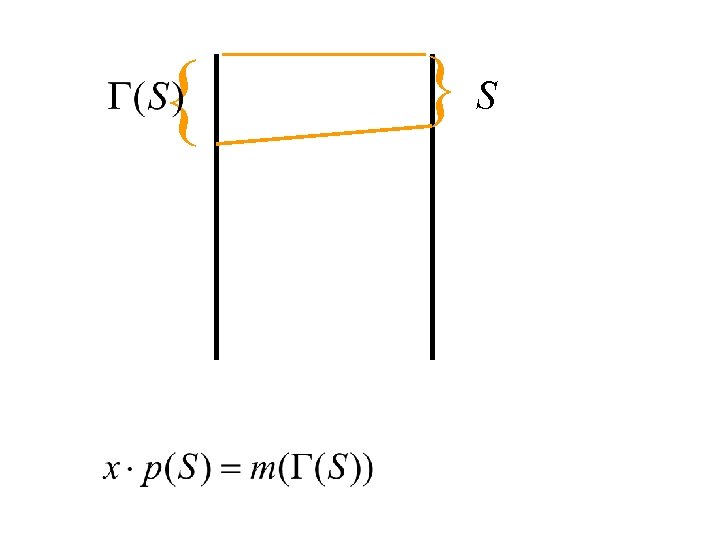
{ }S
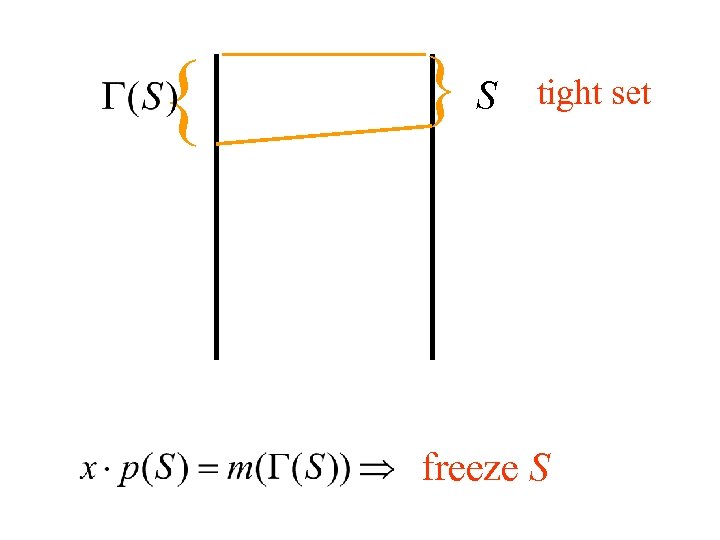
{ }S tight set freeze S
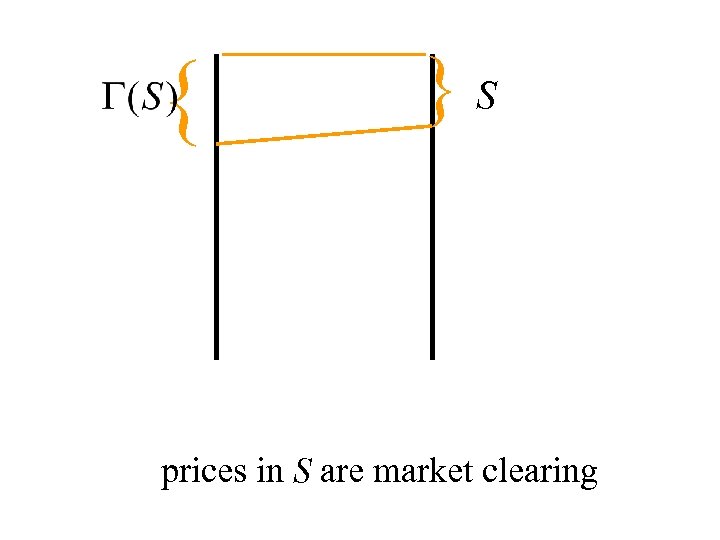
{ }S prices in S are market clearing
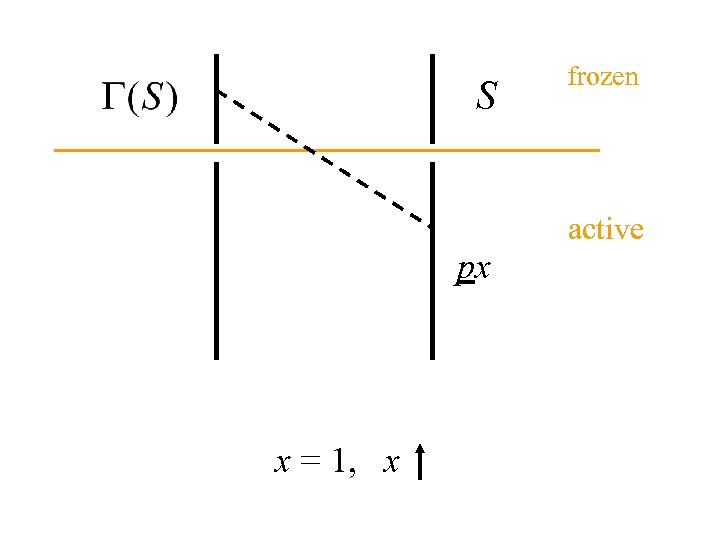
S frozen active px x = 1, x
S frozen active px x = 1, x
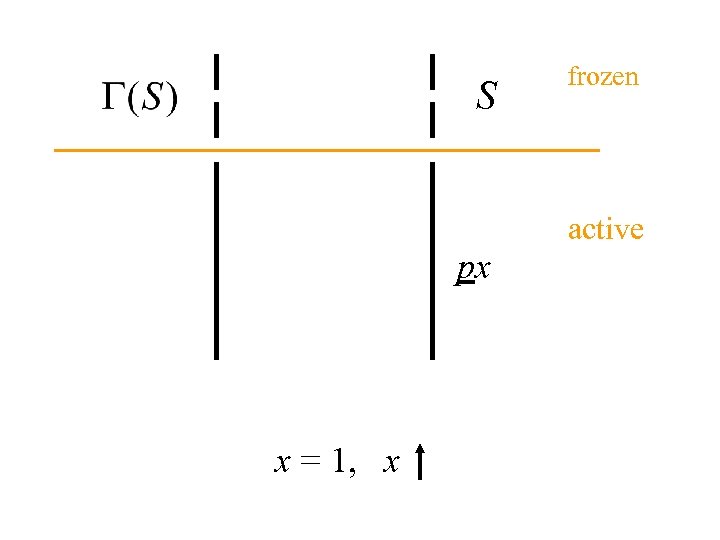
S frozen active px x = 1, x
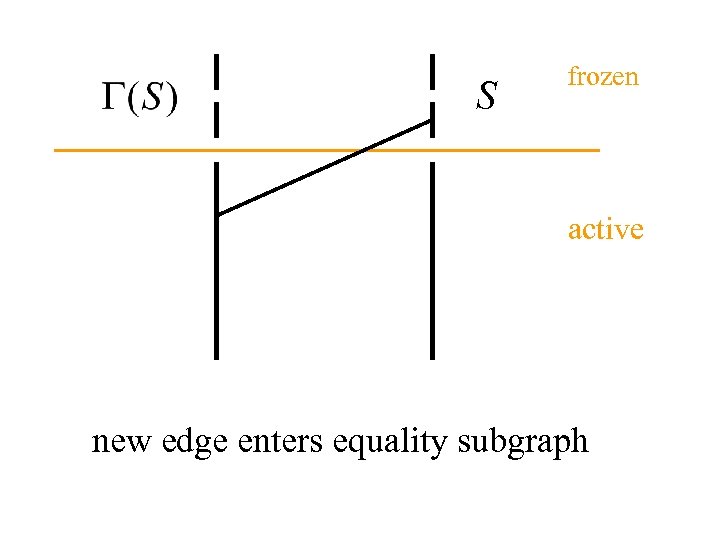
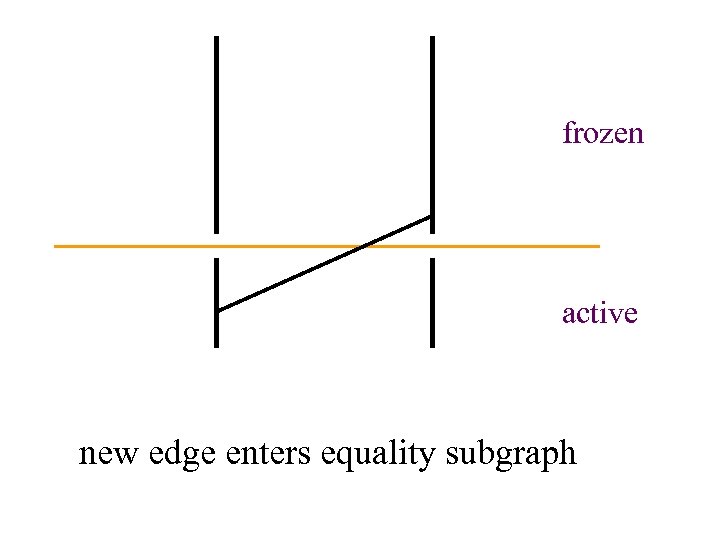
S frozen active new edge enters equality subgraph
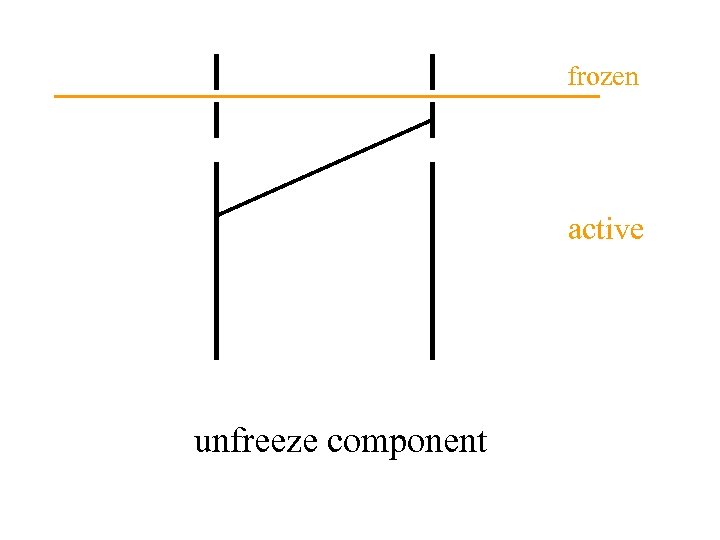
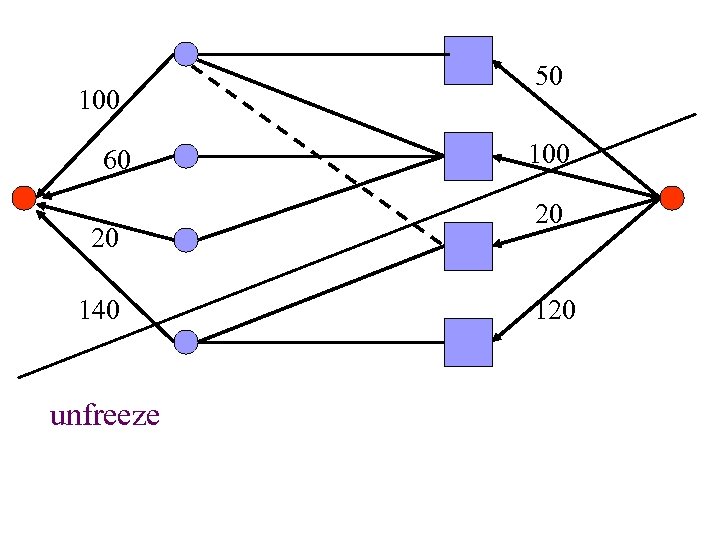
frozen active unfreeze component

• All goods frozen => terminate (market clears)

• All goods frozen => terminate (market clears) • When does a new set go tight? • Solve as parametric cut problem

Termination n Prices in S* have denominators n Terminates in max-flows.

Polynomial time? n Problem: very little price increase between freezings

Polynomial time? n Problem: very little price increase between freezings n Solution: work with buyers having large surplus
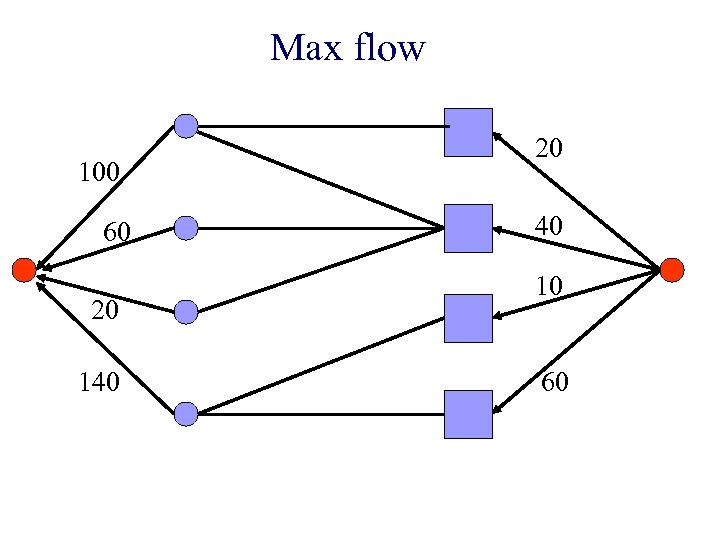
Max flow 100 60 20 140 20 40 10 60
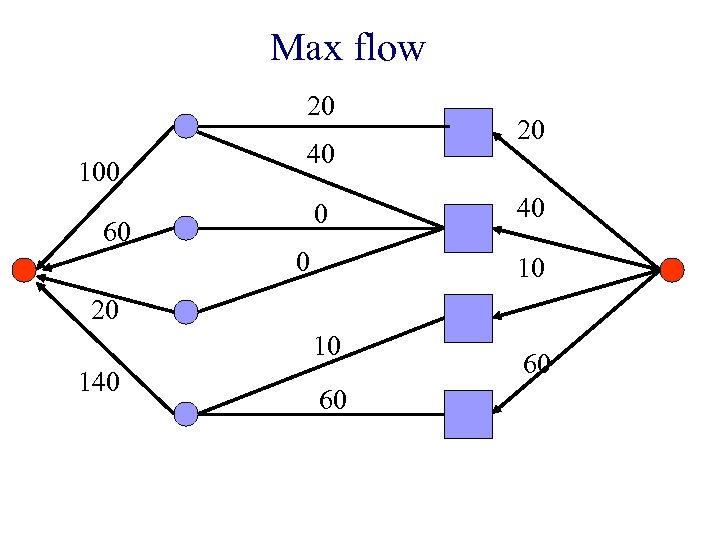
Max flow 20 100 60 40 0 0 20 40 10 20 10 140 60 60
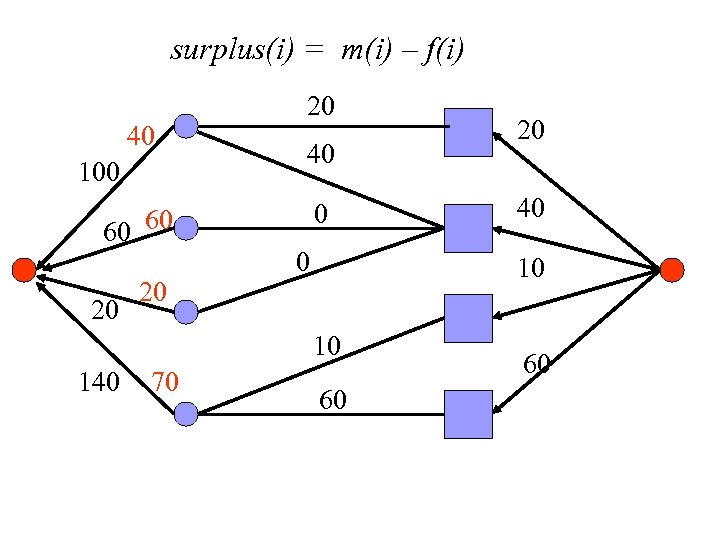
surplus(i) = m(i) – f(i) 40 100 60 60 20 20 20 40 0 0 70 40 10 10 140 20 60 60
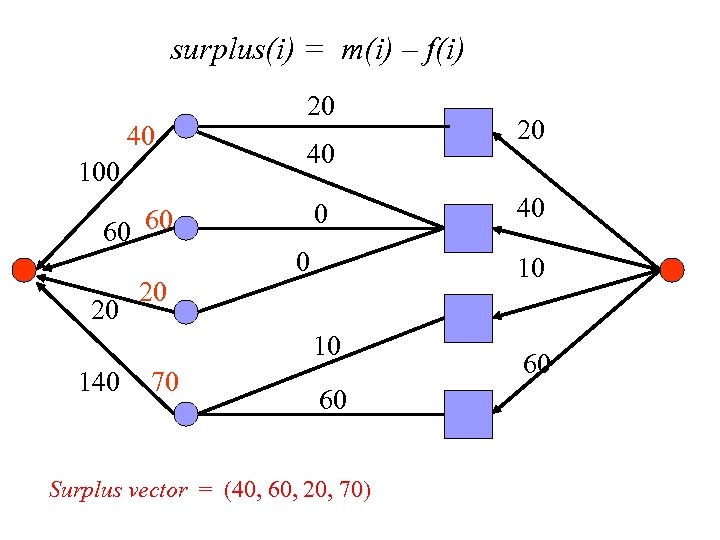
surplus(i) = m(i) – f(i) 40 100 60 60 20 20 20 40 0 0 70 40 10 10 140 20 60 Surplus vector = (40, 60, 20, 70) 60

Balanced flow n A max-flow that minimizes l 2 norm of surplus vector ¨ tries to make surpluses as equal as possible

Algorithm n Compute balanced flow
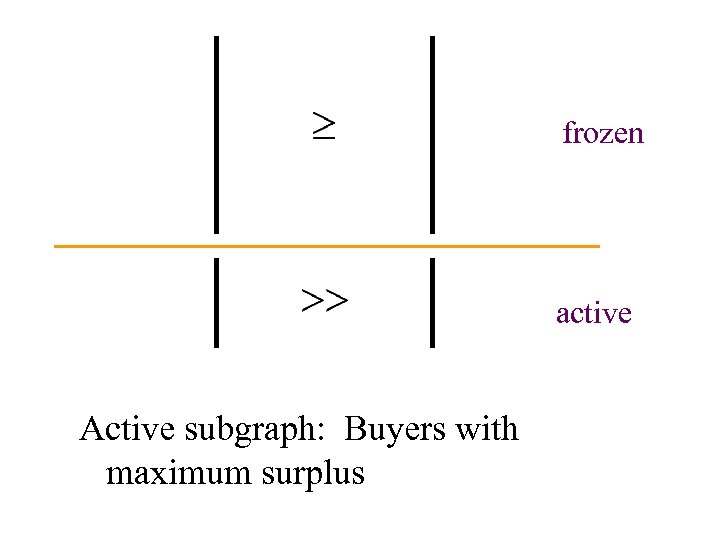
frozen active Active subgraph: Buyers with maximum surplus
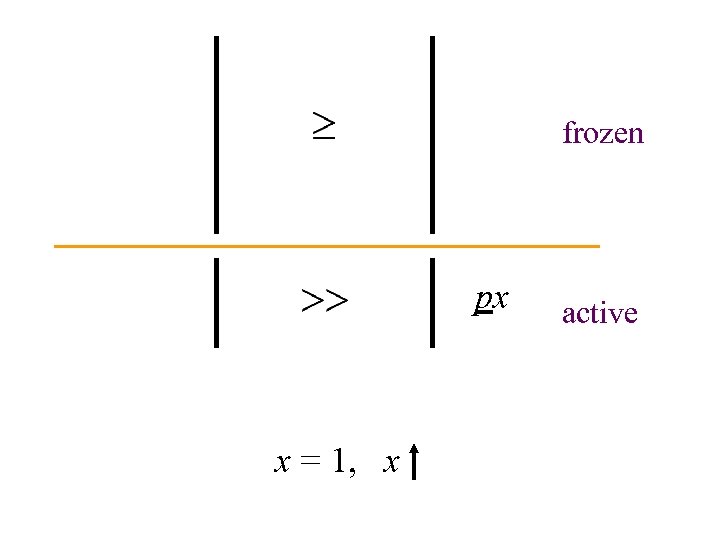
frozen px x = 1, x active
frozen active new edge enters equality subgraph
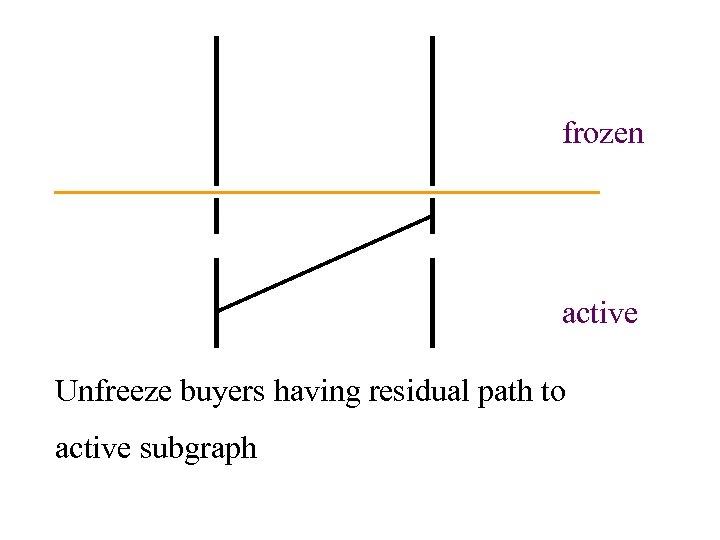
frozen active Unfreeze buyers having residual path to active subgraph
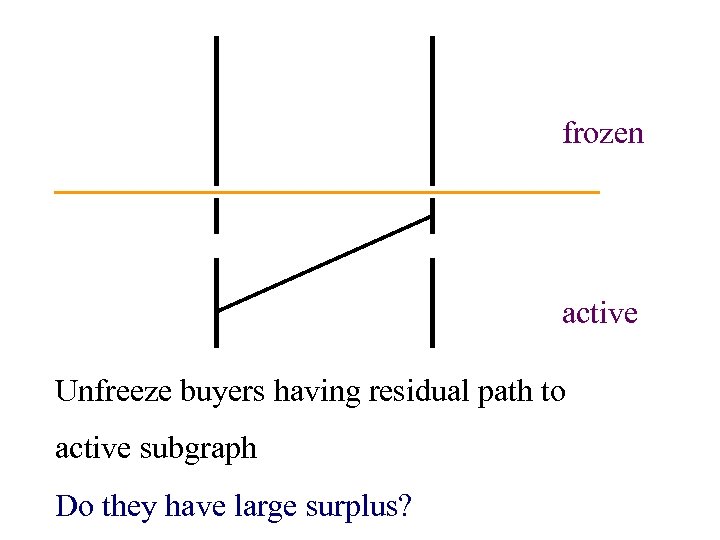
frozen active Unfreeze buyers having residual path to active subgraph Do they have large surplus?

f: balanced flow R(f): residual graph Theorem: If R(f) has a path from i to j then surplus(i) > surplus(j)
frozen active New set tight
frozen active New set tight: freeze

Theorem: After each freezing, l 2 norm of surplus vector drops by (1 - 1/n 2 ) factor. n Two reasons: ¨ total surplus decreases ¨ flow becomes more balanced

Idea of Algorithm n algorithm: primal & dual improvements Allocations n Prices measure of progress: l 2 -norm of surplus vector

Polynomial time Theorem: max-flow computations suffice.

Weak gross substitutability n Increasing price of one good cannot decrease demand for another good.

Weak gross substitutability n Increasing price of one good cannot decrease demand for another good. => never need to decrease prices (dual variables).

Weak gross substitutability n Increasing price of one good cannot decrease demand for another good. => never need to decrease prices (dual variables). n Almost all primal-dual algs work this way.

Arrow-Debreu Model n Approximate equilibrium algorithms: ¨ Jain, Mahdian & Saberi, 2003: Use DPSV as black box. ¨ Devanur & V. , 2003: More efficient, by opening DPSV.

Garg & Kapoor, 2004 Auction-based algorithm n Start with very low prices n Keep increasing price of good that is in demand n B has excess money. Favorite good: g Currently at price p and owned by B’ n B outbids B’
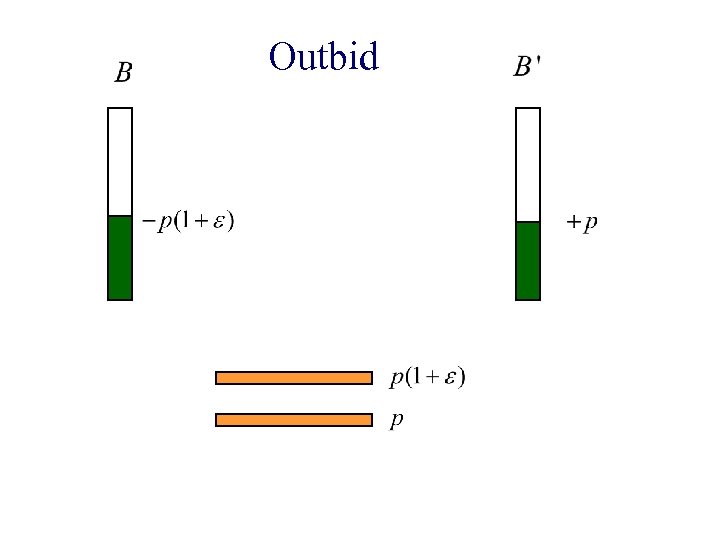
Outbid

Auction-based algorithm n Go in rounds: n In each round, total surplus decreases by factor n Hence iterations suffice, M= total money

Arrow-Debreu Model n n n Start with all prices 1 Allocate money to agents (initial endowment) Perform outbid and update agents’ money

Arrow-Debreu Model n Start with all prices 1 Allocate money to agents (initial endowment) Perform outbid and update agents’ money n Any good with price >1 is fully sold n n

Arrow-Debreu Model n Start with all prices 1 Allocate money to agents (initial endowment) Perform outbid and update agents’ money n Any good with price >1 is fully sold n Eventually every good will have price >1 n n

n Garg, Kapoor & V. , 2004: Auction-based algorithms for additively separable concave utilities satisfying weak gross substitutability

n Kapoor, Mehta & V. , 2005: Auction-based algorithm for a (restricted) production model

Q: Distributed algorithm for equilibria? n Appropriate model? n Primal-dual schema operates via local improvements
6be19a4c92e4974e345147f4d7c7d6be.ppt