COM 1721 Freshman Honors Seminar A Random Walk

COM 1721: Freshman Honors Seminar A Random Walk Through Computing Rajmohan Rajaraman Tuesdays, 5: 20 PM, 149 CN

Introduction n n Explore a potpourri of concepts in computing 1: a mixture of flowers, and applications Theory, examples, herbs, and spices that is usually kept in a jar and used for scent Readings: Handouts and WWW 2: a miscellaneous collection Etymology: French pot pourri, literally rotten pot Grading: Quizzes, homework, and class participation

Sample Concepts n n n n Abstraction Modularity Randomization Recursion Representation Self-reference …

Sample Topics n n n n Dictionary search Structure of the Web Self-reproducing programs Undecidability Private communication Relational databases Quantum computing, bioinformatics, …

Abstraction n n A view of a problem that extracts the essential information relevant to a particular purpose and ignores inessential details Driving a car: n n Building a house: n n We are provided a particular abstraction of the car in which we only need to know certain controls Different levels of abstraction for house owner, architect, construction manager, real estate agent Related concepts: information hiding, encapsulation, representation

Modularity n n n Decomposition of a system into components, each of which can be implemented independent of the others Foundation for good software engineering Design of a basic processor from scratch

Representation n n To portray things or relationship between things Knowledge representation: model relationship among objects as an edgelabeled graph Data representation: bar graphs, histograms for statistics Querying a dictionary; Web as a graph

Randomization n n An algorithmic technique that uses probabilistic (rather than deterministic) selection A simple and powerful tool to provide efficient solutions for many complex problems Has a number of applications in security Cryptography and private communication

Recursion n A way of specifying a process by means of itself n n n Complicated instances are defined in terms of simpler instances, which are given explicitly Closely tied to mathematical induction Fibonacci numbers

Self-reference n n A statement/program that refers to itself Examples: n n “This statement contains five words” contains six words” is not self-referential” is false” n Important concept in computing theory Undecidability of the halting problem, selfreproducing programs n Gödel Escher Bach: an Eternal Golden Braid, n Douglas Hofstader

Illustration: Representation n n Problem: Derive an expression for the sum of the first n natural numbers 1 + 2 + 3 + … + n-2 + n-1 + n = ?

Sum of First n Natural Numbers 1 + 2 + 3 + … + 98 + 99 + 100 = S 100 + 99 + 98 + … + 3 + 2 + 1 = S 101 + … + 101 = 2 S S = 100*101/2 S = n(n+1)/2

A Different Representation 1 2 3

A “Geometric Derivation”

Other Equalities n Sum of first n odd numbers n n 1 + 3 + 5 + … + 2 n-1 = ? Sum of first n cubes n 1 + 4 + 9 + 16 + … + n^3 = ?

Representation and Programming n Representation is the essence of programming Brooks, “The Mythical Man-Month” n Data structures

Dictionary n A collection of words with a specified ordering n n n Dictionary of English words Dictionary of IP addresses Dictionary of NU student names

Searching a Dictionary n n Suppose we have a dictionary of 100, 000 words Consider different operations n n Search for a word List all anagrams of a word Find the word matching the largest prefix What representation (data structure) should we choose?

Search for a Word n n Store the words in sorted order in a linear array Unsuccessful search: n n compare with 100, 000 words Successful search: n on average, compare with 50, 000 words

Twenty Questions n n n n Compare with 50, 000 th word If match, then done If further in dictionary order, search right half If earlier in dictionary order, search left half Until word found, or search space empty Recursion Binary search

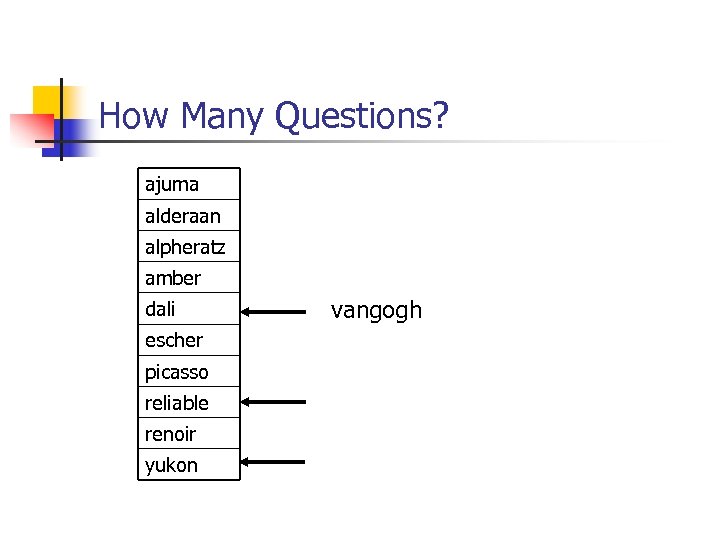How Many Questions? ajuma alderaan alpheratz amber dali escher picasso reliable renoir yukon vangogh

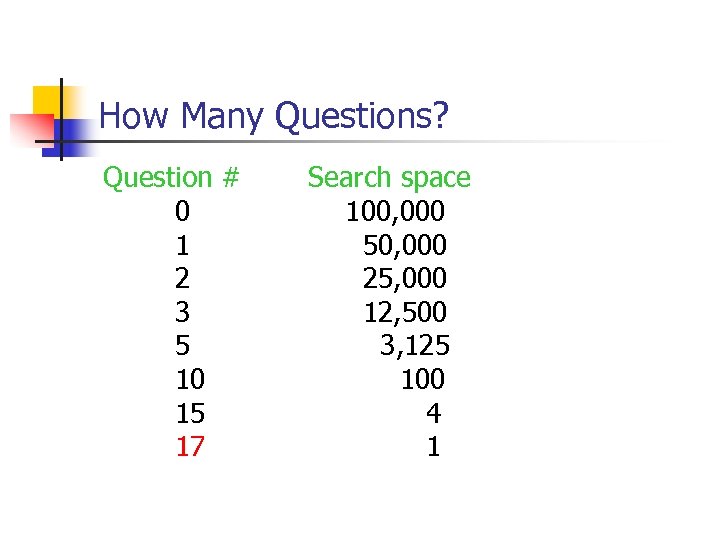How Many Questions? Question # 0 1 2 3 5 10 15 17 Search space 100, 000 50, 000 25, 000 12, 500 3, 125 100 4 1

Anagrams An anagram of a word is another word with the same distribution of letters, placed in a different order n Input: deposit Output: posited, topside, dopiest n Anagrams: subessential suitableness n

Detecting Anagrams n How do you determine whether two words X and Y are anagrams? n n n Compare the letter distributions Time proportional to number of letters in each word Suppose this subroutine anagram(X, Y) is fast

Listing Anagrams of a Word n n Dictionary of 100, 000 English words List all anagrams of least How should we represent the dictionary? Linear array n n Loop through dictionary: if anagram(X, least), include X in list Running time = 100, 000 calls to anagram()

A Different Data Structure n n If X and Y are anagrams of each other, they are equivalent; the list of anagrams of X is same as the list for Y This indicates an equivalence class of anagrams! deposited topside dopiest race care acre adroitly dilatory idolatry

Anagram Signatures n n n Would like to store anagrams in the same class together How do we identify a class? Assign a signature! Sort all the letters in the anagram n Same for each word in a class! acre race care: deposited topside dopiest: subessential suitableness: n word(s) acer deiopst abeeilnssstu

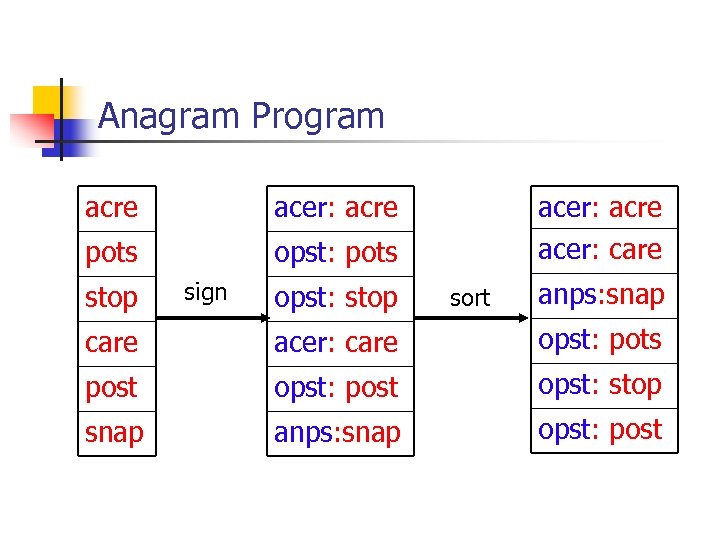Anagram Program acre acer: acre pots opst: pots stop sign opst: stop acer: acre acer: care sort anps: snap care acer: care opst: pots post opst: stop snap anps: snap opst: post

Anagram Program acer: acre acer: care anps: snap opst: pots opst: stop opst: post acer: acre care merge anps: snap opst: pots stop post

Listing Anagrams for Given Word X n n Compute sign(X) and lookup sign(X) in dictionary using binary search List all words in list adjacent to sign(X) post sign opst lookup acer: acre care anps: snap opst: pots stop post

Efficiency of Anagram Program n Once dictionary has been stored in new representation: n n n What about the cost of new representation? n n n Lookup takes at most 17 queries Listing time is proportional to number of anagrams in the class Sign each word, sort, and merge Expensive, but need to do it only once! Preprocessing

References n Programming Pearls, by Jon Bentley, Addison-Wesley n Great Ideas in Theoretical Computer Science, Steven Rudich A course at CMU