Collusion in the Champagne Fairs Controlling Law

Collusion in the Champagne Fairs : Controlling Law Merchants Brishti Guha Singapore Management University

Introduction In Milgrom, North & Weingast (1990), the authors focus on the role of a law merchant (LM) in sustaining medieval trade in the Champagne fairs. The LM adjudicated disputes among pairs of traders and provided a centralized source of information about each trader’s past.

However, what is to prevent a trader from colluding with the LM, bribing him to suppress a history of past cheating? We argue that MNW’s model is not collusion-proof. We present a modified model of medieval trade, showing that a collusion-proof mechanism can be designed. In the process we add 2 institutions – a merchant guild and a competing trade fair.

A Quick Summary of MNW The Champagne Fairs were the focus of international trade in medieval Europe. A trader at the fair could query the LM (at a cost Q) about a potential partner’s past. If the information was satisfactory he traded. If he believed himself cheated he appealed to the LM at a cost C.

The LM would deliver a judgment J in his favor if his appeal was valid, but 0 if it was not. The accused, if the judgment went against him, could then pay – at cost f(J) – or refuse to do so. If he refused, this fact would be recorded by the LM and reported to potential future partners who queried about him. The LM earned a revenue ε from each trader who queried him.

MNW derive parameters such that in equilibrium there exists a judgment J* such that every trader who has no unpaid judgments against him queries the LM and trades if the LM reports a clean record. Honesty is ensured by the credible threat of appeal (as long as C

Each merchant’s payoffs from honesty and cheating have the traditional prisoner’s dilemma structure and are constants. The LM’s role is to provide a centralized source of info. A cheat can be punished by all potential future matches without the need for continuous multilateral info exchange.

But is their Model Collusion-Proof? No. Suppose a merchant cheats and does not pay the judgment (fine). He may bribe the LM to suppress this. Such collusion is undetectable in the model. The LM will report a clean previous record to future partners who query about the cheat.

If they are subsequently cheated, no blame attaches to the LM in keeping with MNW’s strategy. The cheated merchants simply appeal to the LM who then orders the cheat to pay a fine – an order which cannot be forcibly implemented. As the LM can collude without penalty, he has an incentive to accept a bribe.

A dishonest trader also has an incentive to bribe the LM by paying him a fraction of his one time cheating gains. He then gains and suffers no future penalty as the LM erases records of his misdeed. Thus the system will unravel.

Collusion-Proofing the Model : Fairs, Guilds and Competition Actual practice at the Champagne Fairs differed from MNW’s model. Fair authorities controlled access to the fair. A cheat could be debarred from future fairs. Collusion would amount to letting a cheat with an unpaid judgment enter a future fair. Unlike in MNW’s model such collusion could be detectable.

Changes in Assumptions Our assumptions differ from MNW’s : We allow payoffs from attending a fair to be a function of the number of other merchants at that fair. We introduce competition from a rival trade fair. We let merchants belong to a guild (not all merchants who attend the same trade fair have to belong to the same guild).

Our Model N merchants, 2 fairs (Champagne + rival). An endogenous number M of the N merchants attend the Champagne fair. Each such merchant’s stage payoffs from honesty and cheating are H(M) and α(M) where α(M) >H(M) for all M and H(M)>H(M-1) for all M.

If the LM was honest he earned a period revenue of εM : each of the M traders at Champagne traded once. However having a larger number of traders attend the fair meant a larger choice set and chances to make contacts for lines of credit & letters of introduction. Competition from a rival fair.

The payoffs to trading honestly at the rival fair are β(n) where n is the total number of merchants at this rival fair : β(0) = β(1) = 0. Merchant specific costs of attending the rival fair relative to Champagne (eg due to locational factors) ranked C 1 to CN (lowest to highest). C 1<0 (otherwise rival fair would not emerge, given Champagne’s first mover advantage).

The nth merchant will choose the rival fair over Champagne only if β(n) – H(N-n + 1) > Cn Both the LHS and RHS are increasing in n. Consider a class of functions with – H(N) > C 1 β(N) – H(1) > CN

There exists some n between 1 and N for which β(n) – H(N-n+1) < Cn For this class of functions there is an even number of intersections between the LHS and RHS. In the case shown with 2 intersections, the one further to the left is stable : the other is unstable.

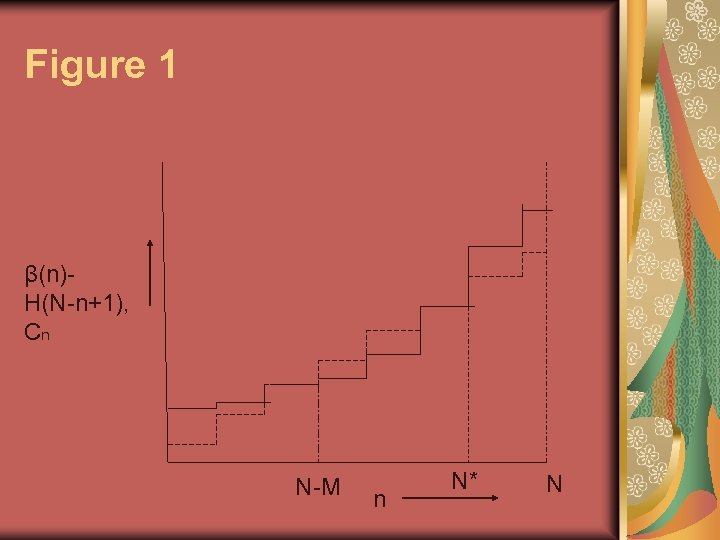Figure 1 β(n)H(N-n+1), Cn N-M n N* N

So in the initial equilibrium we have NM merchants in the rival fair and M in Champagne (now M is endogenized). If n were to reach N*, all the merchants would abandon the Champagne fair in favor of the rival fair.

Detecting Collusion and the Role of the Guild A cheated merchant may observe a merchant who cheated him (and left without paying a judgment) at a future fair and infer collusion between the cheat and the LM (the Champagne fair authority). If the cheated merchant belongs to a guild he can then inform the guild about the Champagne fair’s unreliability.

If spreading info to others is so easy, why have a LM at all (a la Greif (1993))? Answer : easier to monitor fairs (which were much smaller in number) than individual merchants. Also a fair had independent benefits from a large number of traders congregating at one place. The cheated merchant’s guild could organize a collective boycott of the Champagne fair.

We show that if the guild has enough members (G>N*-(N-M)), no individual guild member has an incentive to deviate from the collective punishment. Intuition : at this point, it is simply more profitable to attend the rival fair, given that so many others are doing so.

The self-enforcing nature of the punishment does not depend on the assumption that the Champagne fair must continue to be dishonest in future periods. Nor does it depend on the assumption that a deviant guild member would be punished by the rest of the guild.

But once n moves beyond N* (which is unstable) it tends to jump all the way to N : other merchants outside the guild find it profitable to abandon Champagne in favor of the rival fair, even though they are not participating in the punishment. This may happen with a lag.

The LM’s no-collusion condition α(M) – H(M) – Q < p[δεG + δ 2εM/(1 -δ)] where δ is the discount factor and p is the probability of the LM’s collusion being detected. LHS = maximum bribe LM can get (cheating gains net of querying costs). RHS = discounted losses (from only the guild merchants in the next period, and from all M Champagne fair attendees afterwards).

Conclusion Modified and extended MNW’s model to derive conditions under which the Champagne fair could function without collusion. We pointed out that MNW’s model was not collusion proof : collusion was undetectable and the system would unravel. Our model tries to fit the reality of the Champagne fairs more closely.

Once this is done it is not hard to think of mechanisms that allow collusion to be detected. We introduce a competing fair and a merchant guild which can organize collective boycotts. We derive conditions under which a transgression against one trader by the LM would lead to a collective boycott from which no one guild member would want to deviate.

Moreover the presence of a competitor encourages even merchants outside the punishing guild to abandon the Champagne fair.