1b22feb08263e5a7344e5b9ca870d0c7.ppt
- Количество слайдов: 55

Collision Detection Design & Final Project Topic Brandon Smith November 5, 2008 ME 964

contact_data Allocation • Possible ways to allocate the contact_data array: – Allocate contact_data[ N(N-1)/2 ] – Allocate contact_data[ n_contacts ] • To avoid creating a huge array, I chose the second method: – 1 st Kernel Call • Find the number of contacts. – 2 nd Kernel Call • Calculate the contact_data for each contact.

Kernel Call Setup • The total number of contact tests is: n_tests = N(N-1)/2 • The total number of concurrent threads is: n_concurrent_threads = N_SMs * BLOCKS_PER_SM * THREADS_PER_BLOCK • Each thread will perform several tests: n_test_per_thread = n_tests / n_concurrent_threads + 1

Collide Kernel: Indexing • Given the block number and thread number, a range of test numbers (ki, kf) are generated: thread_id = bx*THREADS_PER_BLOCK + tx; ki = tests_per_thread*thread_id + 1; kf = ki + tests_per_thread - 1; • Given a test number k, the indices (i, j) can be calculated: Body 1 2 3 4 k = ( (j-1)2 -(j-1) )/2 + I k <= (j 2 -j )/2 1 2 3 4 i 1 j 2 4 7 3 5 8 6 9 k

Collide Kernel: Contact Testing • __global__ function calls __device__ test to actually perform the contact test • In the first pass it simply tests for contact • In the second pass it calculates contact_data. • atomic. Add is used to count the number of contacts – Keeps one contact tall for all concurrent threads – No need for condensation of results from each thread – Hassle to compile: nvcc. exe -ccbin "C: Program FilesMicrosoft Visual Studio 8VCbin" -c -arch sm_11 -D_CONSOLE -Xcompiler "/EHsc /W 3 /nologo /Wp 64 /O 2 /Zi /MT " I"C: CUDAinclude" -I"C: Program FilesNVIDIA CorporationNVIDIA CUDA SDKcommoninc" -o Releasecollide. obj collide. cu
Final Project: Monte Carlo Radiation Transport • Objective: – Compute radiation flux or derived quantities over a spatial/temporal domain. • Method: – Follow the life of individual particles through the domain. • Quality of Results: – Statistical error is proportional to 1/sqrt(n_particles) – Difficult to get even particle distribution across the domain – Many particles are required to achieve low statistical error
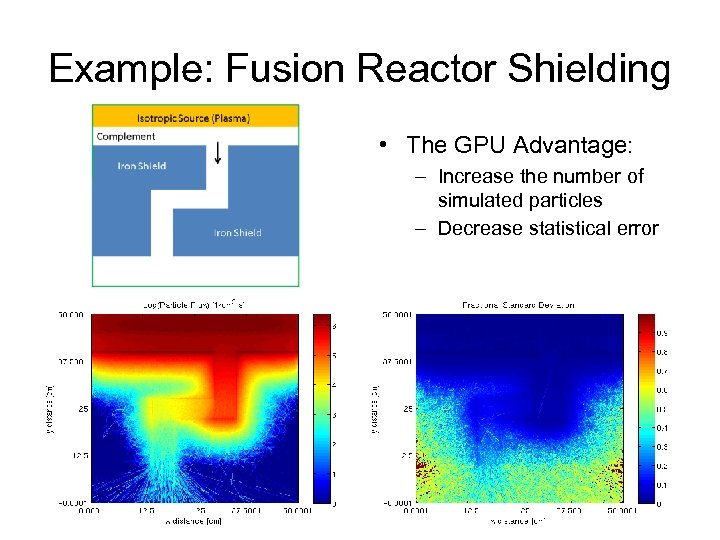
Example: Fusion Reactor Shielding • The GPU Advantage: – Increase the number of simulated particles – Decrease statistical error

Tasks during a Particle’s Life • Birth: particles are created at a source • Ray-cast: the distance to the next surface is calculated • Collision: the particle interacts with matter • Next volume: the particle crosses a boundary into another material • Death: if the particle is absorbed, it is killed.

Existing Fortran Code • Geometry: – 3 -D geometry supporting boxes and spheres • Physics: – Only neutral particles (neutrons, photons) – No energy dependence – No time dependence • Materials: – Simple materials (only a few isotopes) • Sources: – point, line, area, volume • Results: – mesh tallies and volume tallies

Potential for Parallelism • Usually we can assume each particle is independent, unless: – criticality, weight windows, etc… • Each thread could calculate independent particle trajectories – embarrassingly parallel • When enough particles are simulated, condense the results from each thread

Implementation Challenges • Current code is in Fortran 90 – ~1700 lines – Has anyone tried F 2 C? • Designed for Fortran 77 • Particles are tracked on a large mesh – ~1 M mesh elements, accessed once per particle – Mesh will need to be in global memory – Mesh will be accessed with an atomic function for data sharing? • Ensure that random numbers are not repeated – Use a pseudo-random number generator for each thread – Each thread will need a different random seed – Check to ensure sufficiently large stride • Could schedule rendezvous to check for solution convergence – Stop simulation once statistical error falls below a set value ( 5% )

ME 964: Project Proposal Vikalp Mishra

Collision Detection • Aim – Solve collision detection problem given N rigid spheres in 3 D space • Approach – Brute Force – Compare each sphere with every other sphere • O(n 2) – If distance between centers is • more than sum of radii No collision • Less than sum of radii Collision – When collision detected • compute normal and object IDs
Final Project: Bone FEA • Title: – GPU based Finite Element Analysis of Femur • Femur – Thigh bone: Bone between hip and knee joint – Longest/ strongest bone in the body

Why study femur ? • To better understand bone mechanics/ properties – Across species • To understand the impact & extent of injury under various loading – Use in sports medicine & surgery • To study impact of DNA change on bone

Background • In past – Experiments were done to study bone behavior / material properties • Test performed – Fracture test – Bending test – Torsion test • Experiments on mouse / pig – Costly and time consuming – Only one experiment per sample possible • Alternative – Capture bone geometry and material properties – Use computational tools for various analysis
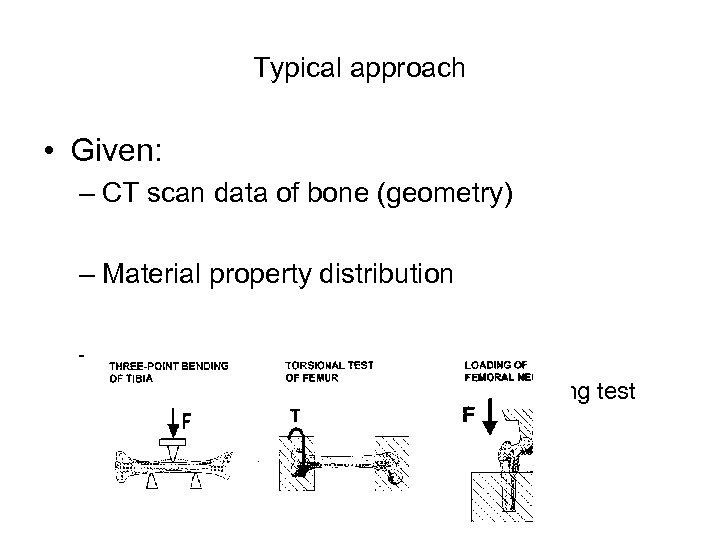
Typical approach • Given: – CT scan data of bone (geometry) – Material property distribution – Loading scheme • 3 or 4 point loading / Torsion test / Bending test

Use of FEA • Use Finite Element Method – To capture geometry – Physical properties • Hexahedral elements • Tetrahedral elements • Formulate FE problem – Use boundary conditions to define element level • stiffness matrix (Ke) • load vector (Fe) • Assemble elements in global matrix (Kg, Fg) • Solve FE problem – Obtain deflection (u = Kg-1 Fg) • Compare with experimental results

Bottleneck • Bone geometry is complex – Large number of elements required • For pig bone ~ 0. 5 – 1 million elements (coarse mesh)

GPU based approach • Potential for GPU based computation – Same set of computation for each element • Stiffness matrix computation (Ke) • Load vector computation (Fe) – Different data sets for each element – SIMD • Approach – Use GPU for element level computation

ME 964 – Midterm and Final Projects Saigopal Nelaturi

CUDA Collision detection • Problem – Given n spheres in 3 d space, compute all pair-wise collisions • Approach – Brute force algorithm with quadratic complexity • Idea – every pair of spheres can be tested independently, and in parallel

Task Parallelism – pseudo code

Final Project • Constructive operators in SE(3) • SE(3) is the group of 4 x 4 rigid transformation matrices • Point in SE(3) = matrix • Set in SE(3) = set of matrices • Can devise operators using Boolean algebra and matrix multiplication (group operation)
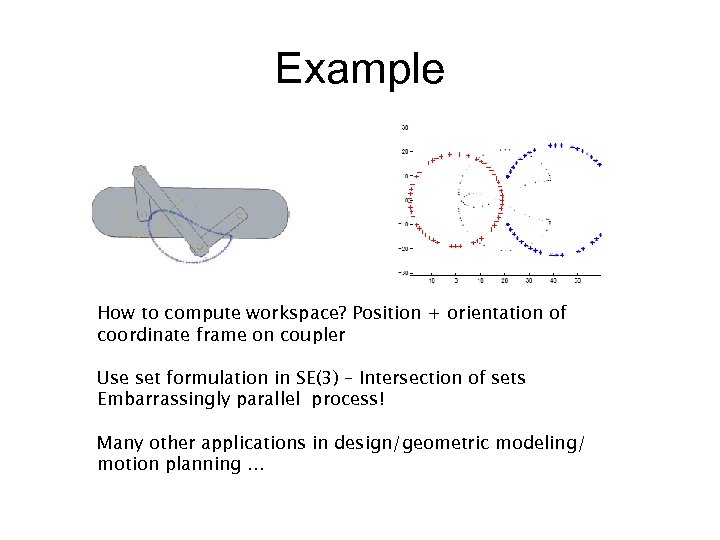
Example How to compute workspace? Position + orientation of coordinate frame on coupler Use set formulation in SE(3) – Intersection of sets Embarrassingly parallel process! Many other applications in design/geometric modeling/ motion planning …

Goals • For very large sets of 4 x 4 transformation matrices , implement • Intersection – pairwise comparison between matrices • Convolution – pairwise multiplication between matrices • Show some workspace computations (hopefully in 3 d) If possible, implement • Deconvolution – combination of pairwise intersection/multiplication

Midterm Project Ram Subramanian

The Task To solve a collision detection problem: Given an arbitrary number of rigid spheres with known radii, distributed in the 3 D space, To find out which spheres are in contact/penetration with which other spheres.

The Algorithm • One pass over array to determine collisions. • One pass over all the collided bodies to compute the values of collision required. • Two Kernel Calls. • O(n. (n-1)/2)

Indexing Every Thread gets a Reference body (Body A) and a Comparison body (Body B). Each block has 512 threads (assumption 1). Each row in a grid has 512 blocks (assumption 2). Total number of threads is n(n-1)/2. Compute the index value with the thread ID and block ID. Using this index value and the number of bodies (using the div and mod) the index of the Body A and Body B, respectively, can be determined.

Final Project - Image Processing on the GPU Goal – Implement Image Processing Algorithms for the GPU. Eventually have an image processing library for the GPUs using CUDA Motivation – Most image processing tasks involve operating on individual pixels or a region of the image. Many of these tasks are embarrassingly parallel.

Proposed Implementations • Harris Corner Detector Motivation – This is an algorithm used in the first stage processing of many other Image Processing and Computer Vision algorithms (e. g. : 3 D reconstruction, Scene Stitching, Object Tracking, Visual Servoing, etc… ) Ambitious Goal Implement an image stitching algorithm or 3 D reconstruction algorithm that will stitch two images together using the Harris Corner detector.

Harris Corner Detector • At every pixel in the image place a window (larger the better, e. g. 5 x 5) call it W • Assume either 4 or 8 neighborhood of the current pixel position • Slide the window to each neighboring pixel, giving W 1, W 2 …Wi (where i = 4 or 8)

Harris Corner Detector Contd. . • Compute the sum of squared differences (SSD) between W and each Wi • A Corner is detected when all SSD values are below a given threshold set by user (or the smallest value is below a given threshold).

Midterm and Final Projects Toby Heyn ME 964 11/06/08
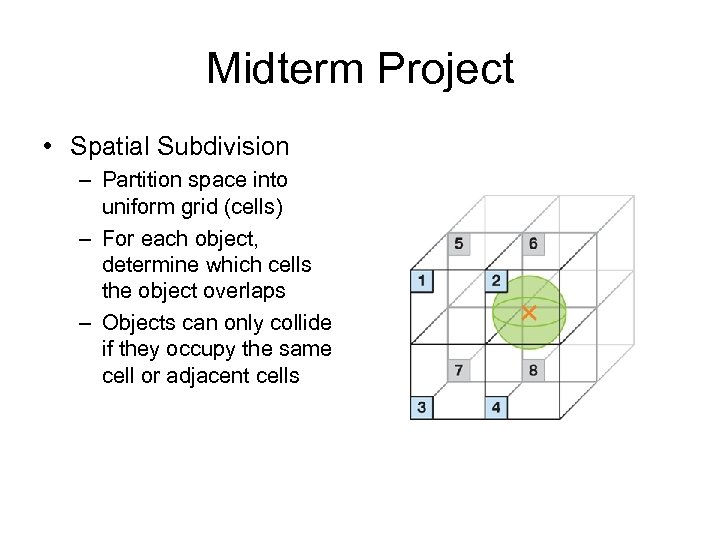
Midterm Project • Spatial Subdivision – Partition space into uniform grid (cells) – For each object, determine which cells the object overlaps – Objects can only collide if they occupy the same cell or adjacent cells

Midterm Project • Construct Cell ID Array – Each thread determines the cell IDs of the cells its sphere occupies, loads into Cell ID Array • Sort Cell ID Array – Radix Sort Algorithm • Create Collision Cell List – Scan sorted Cell ID Array, look for changes in cell ID – Write Collision Cell List with Cell ID Array indices, number of objects in the cell • Traverse Collision Cell List – One thread per Collision Cell – Each thread checks all collision pairs in the Collision Cell – Collisions are written to output

Midterm Project • Radix Sort – Sorts cell IDs in several passes – Sorts low order bits before higher order bits, retaining order of IDs with same cell ID • This helps in a later step – Takes 4 passes to sort the 32 bit (4 byte) integers – Makes use of parallel scan operation

Final Project • Default final project – granular dynamics using collision detection from midterm • Incorporate midterm collision detection into Chrono: : Engine multibody dynamics engine • Simulate Mars Rover with many (millions) of bodies

Final Project • Chrono: : Engine – C++ API – Commands for creating simulation environment, populating with bodies, creating constraints, etc – Uses Bullet for collision detection – Has been used to solve systems with ~100, 000 bodies – Has a CUDA parallelized dynamics solver (based on LCP formulation)

Final Project • Each wheel is a union of primitives • Terrain consists of ~5000 spheres (much too coarse) • Obstacles: – Non spherical bodies in wheels – Large mass difference between small grain and large rover
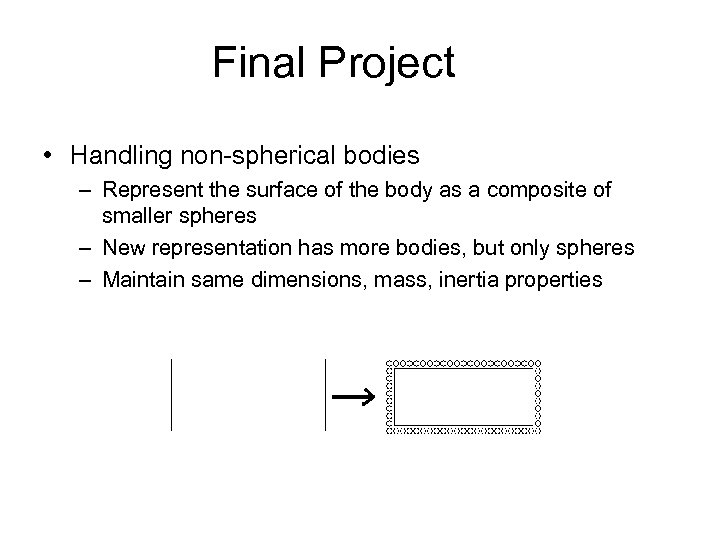
Final Project • Handling non-spherical bodies – Represent the surface of the body as a composite of smaller spheres – New representation has more bodies, but only spheres – Maintain same dimensions, mass, inertia properties

Final Project • Parallelism – Collision detection • Many bodies/collision pairs to check • Spatial sub-division: geometric decomposition, task decomposition – Dynamics • Many equations of motion to solve – Geometric decomposition • Potentially many non-spherical bodies to process in parallel

Final Project • Remaining Issues – Re-use of data • After solving the collision detection problem once, can data be reused to reduce the size of the problem to be solved in subsequent steps? – Automate handling of non-spherical geometry • Can an automated method be created to represent arbitrary geometry with spheres?

ME 964 Midterm & Final Project Justin Madsen

Outline • Midterm & final are the same project – “default scheme” • Collision detection method – Baraff – Brief overview of 2 phase algorithm – Ideas for CUDA implementation • Ideas for final project – Integrating CUDA collision detection with other dynamics programs

Efficient collision detection • Baraff method – Axis Aligned bounding boxes (AABB) – Simple yet efficient – Only dealing with spheres • Can be extended to convex polyhedra • (actually don’t need bounding boxes for spheres, it’s a special case) Figure 1. AABB size and orientation depends on the local coordinate system

Overview of method • One dimensional case (x-axis) • Sort & Sweep – Each object has a length along the axis according to the AABB – Data: beginning and end values (b and e) of each box – Sorted lowest to highest according to these values Figure 2. Six objects and their AABB axes [1]

Determine possible contacts • After sorting, collision detection happens in two phases • Phase 1: broad phase – Traverse the axis; add objects to “possible contact list” when bi is encountered – For one dimensional case, when bi added to the list, it means contact occurs with all other objects in the list

Three dimensional case • Phase 1 for 3 -D: – Extend one dimensional contact check by checking b and e for values along the y and z axes of the other objects in the list – If contact check comes back positive for all 3 axes, add the object to the “possible contact list” • Possible because…

Need to verify collision • Tested positive for collision along all 3 axes… Figure 3. Left to right: XY, XZ and YZ axes testing positive for collision

Verifying collision • Phase 2: narrow phase – Just because all 3 axes “intersect” does not necessarily mean contact has occurred – Remember, checking bounding boxes, not actual object – Using spheres; check distance between spheres vs. respective radii

Implementation in CUDA • Can parallelize both broad and narrow phase – Accomplish this by assigning each object a thread – Same method, but requires two broad phase sweeps • Sweep 1: determine & save number of collisions, but don’t save collision pairs – Do a prefix sum to determine amount of memory and memory location to store each collision pair • Sweep 2: determine collision pairs and save them to the correct memory location

Extending midterm to final project • Collision detection to be used for granular dynamics – Use existing parallel algorithms to determine dynamics of a system with many contacts – Integrate my collision detection program into existing software • Bullet, Chrono. Engine
![References • [1] David Baraff. An introduction to physically based modeling: Rigid body simulation References • [1] David Baraff. An introduction to physically based modeling: Rigid body simulation](https://present5.com/presentation/1b22feb08263e5a7344e5b9ca870d0c7/image-55.jpg)
References • [1] David Baraff. An introduction to physically based modeling: Rigid body simulation II - nonpenetration constraints. SIGGRAPH Course Notes, 1997.
1b22feb08263e5a7344e5b9ca870d0c7.ppt