Скачать презентацию Coherent Sources Wavefront splitting Interferometer Young s Скачать презентацию Coherent Sources Wavefront splitting Interferometer Young s

26170_coherent sources.ppt

  • Количество слайдов: 45

Coherent Sources Coherent Sources

Wavefront splitting Interferometer Wavefront splitting Interferometer

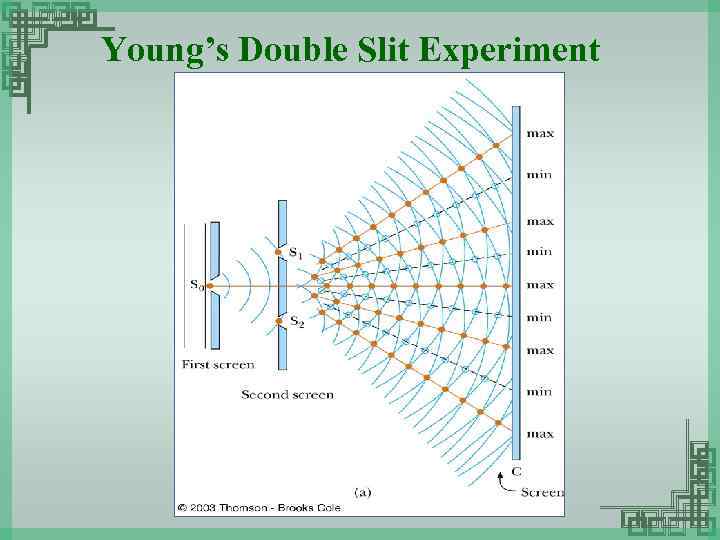Young’s Double Slit Experiment Young’s Double Slit Experiment

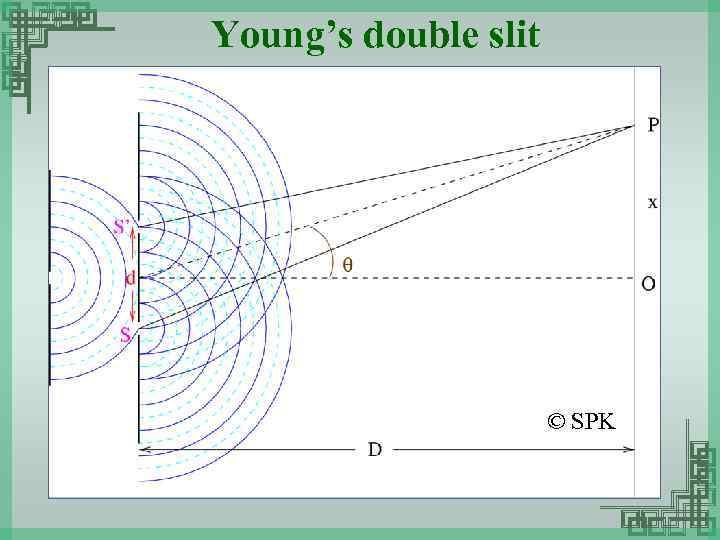Young’s double slit © SPK Young’s double slit © SPK

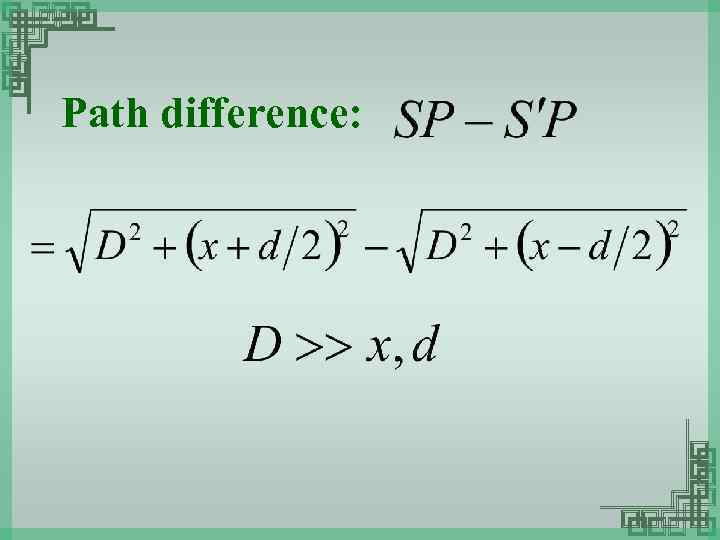Path difference: Path difference:

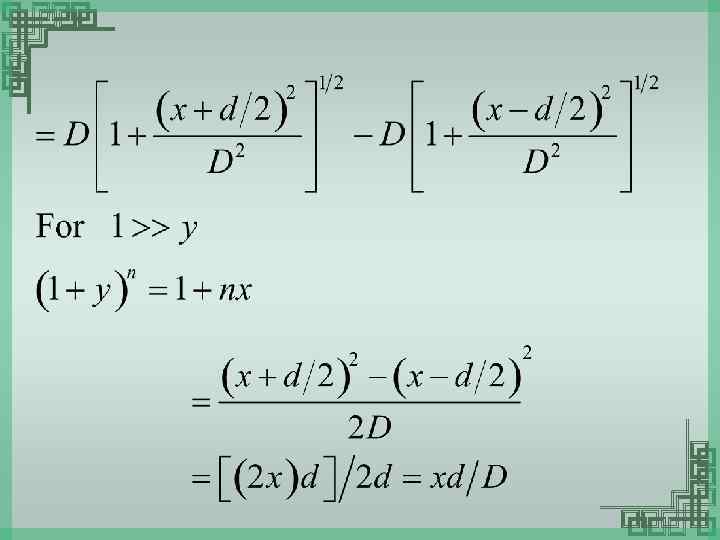
For a bright fringe, For a dark fringe, m: any integer For a bright fringe, For a dark fringe, m: any integer

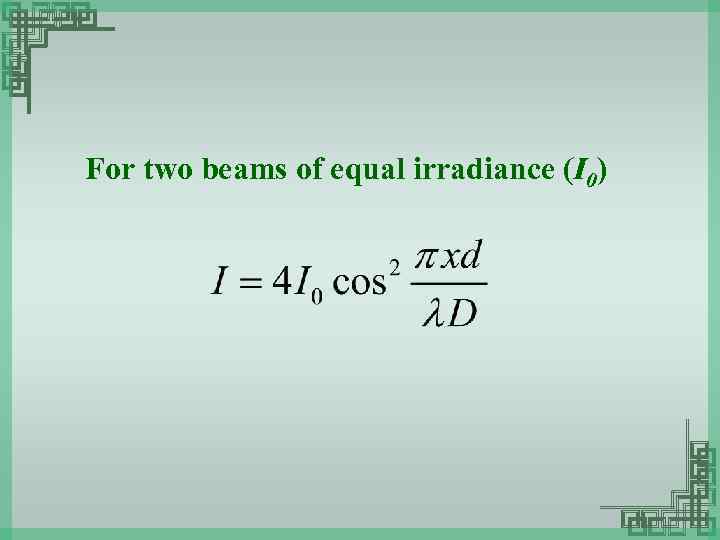For two beams of equal irradiance (I 0) For two beams of equal irradiance (I 0)

Visibility of the fringes (V) Maximum and adjacent minimum of the fringe system Visibility of the fringes (V) Maximum and adjacent minimum of the fringe system

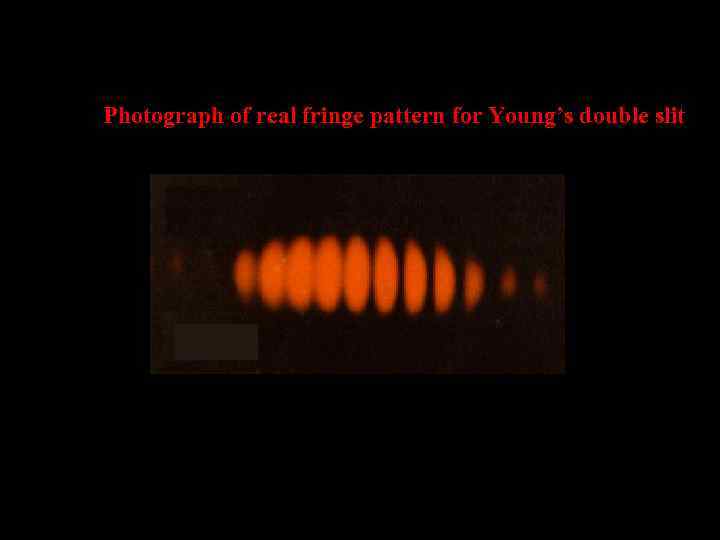Photograph of real fringe pattern for Young’s double slit Photograph of real fringe pattern for Young’s double slit

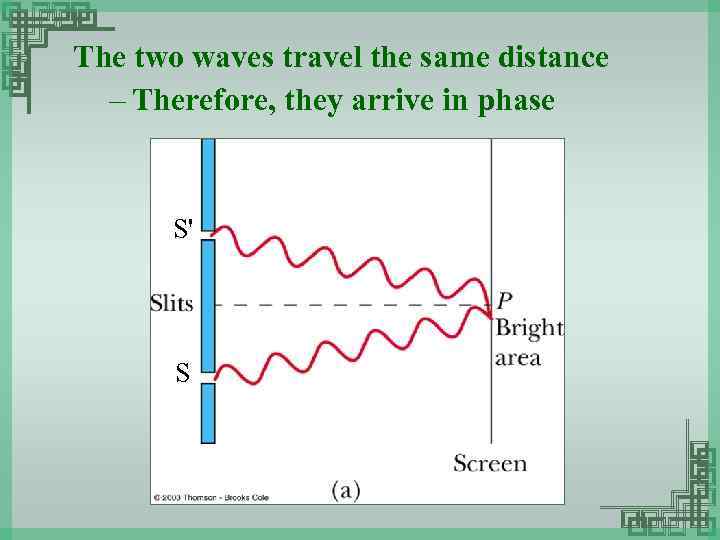The two waves travel the same distance – Therefore, they arrive in phase S' The two waves travel the same distance – Therefore, they arrive in phase S' S

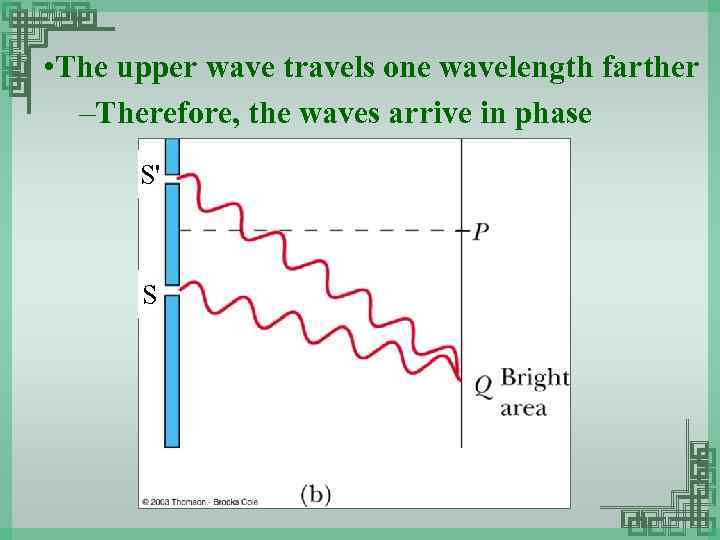• The upper wave travels one wavelength farther –Therefore, the waves arrive in • The upper wave travels one wavelength farther –Therefore, the waves arrive in phase S' S

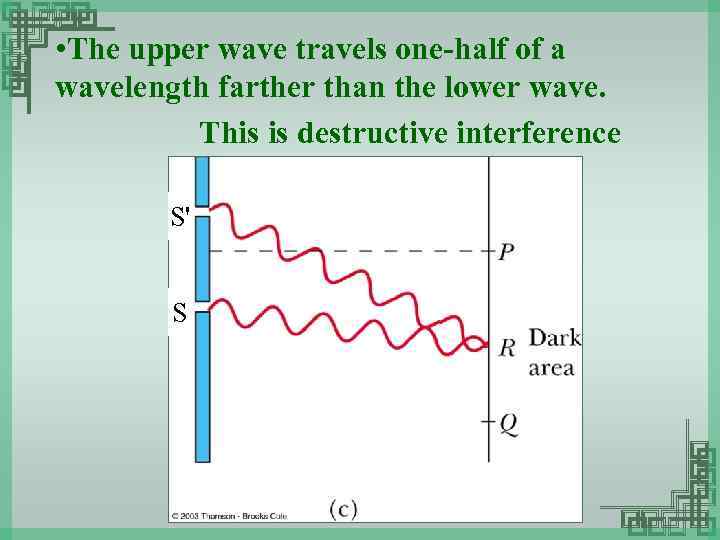• The upper wave travels one-half of a wavelength farther than the lower • The upper wave travels one-half of a wavelength farther than the lower wave. This is destructive interference S' S

Uses for Young’s Double Slit Experiment • Young’s Double Slit Experiment provides a method Uses for Young’s Double Slit Experiment • Young’s Double Slit Experiment provides a method for measuring wavelength of the light • This experiment gave the wave model of light a great deal of credibility.

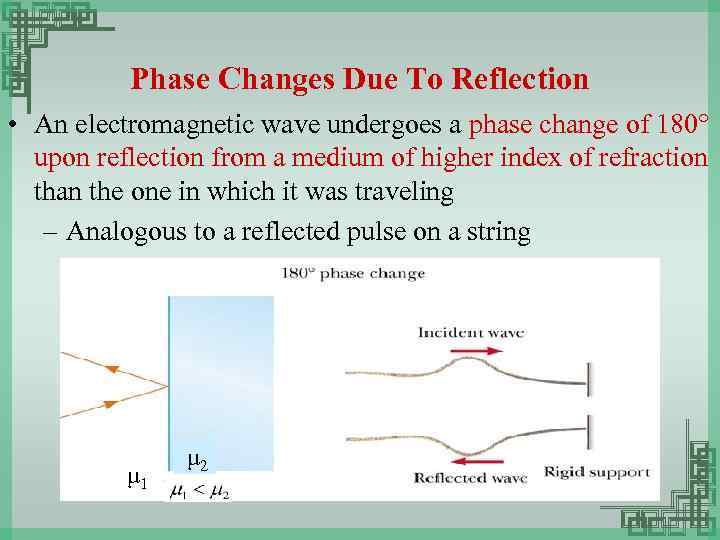Phase Changes Due To Reflection • An electromagnetic wave undergoes a phase change of Phase Changes Due To Reflection • An electromagnetic wave undergoes a phase change of 180° upon reflection from a medium of higher index of refraction than the one in which it was traveling – Analogous to a reflected pulse on a string μ 1 μ 2

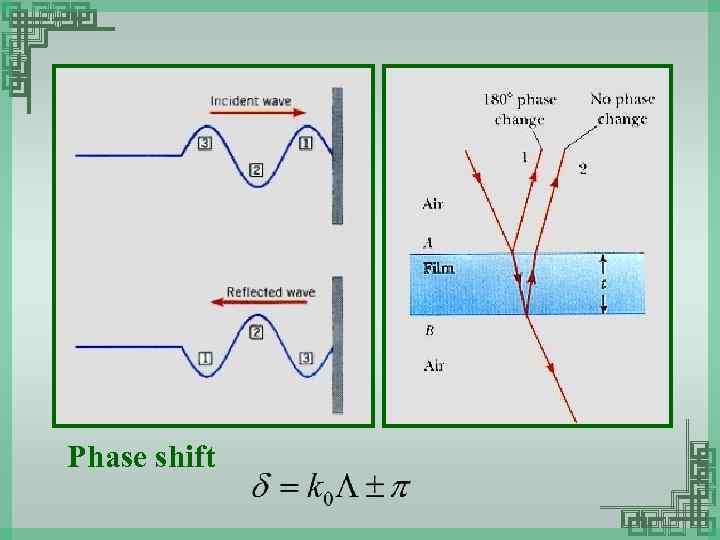Phase shift Phase shift

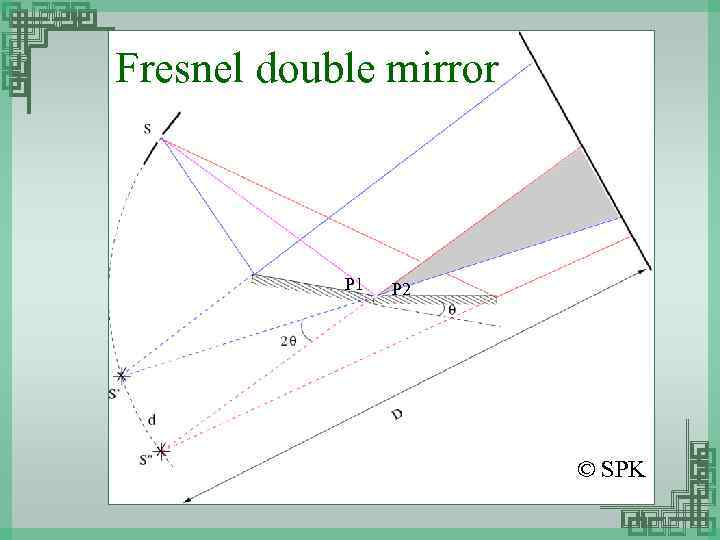Fresnel double mirror P 1 P 2 © SPK Fresnel double mirror P 1 P 2 © SPK

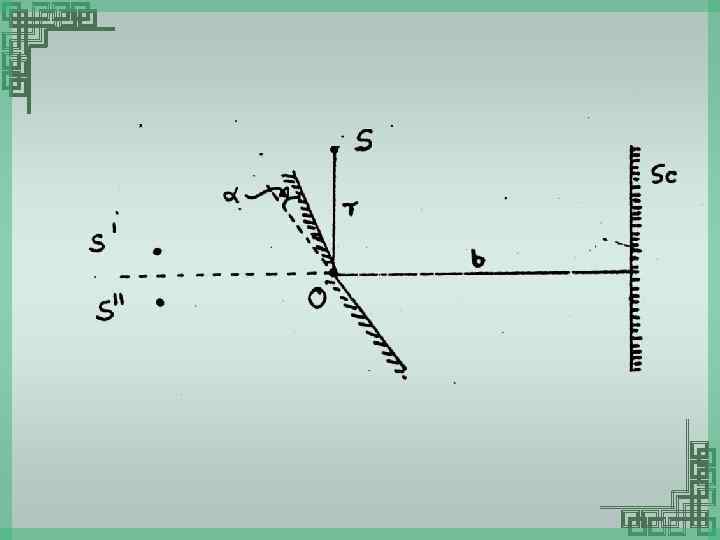
Problem In a Fresnel mirror the angle between the mirrors a=12’. The distance r= Problem In a Fresnel mirror the angle between the mirrors a=12’. The distance r= 10 cm and b=130 cm. Find (a) The fringe width on the screen and the number of possible maxima. (b) the shift of the interference pattern on the screen when the slit S is displaced by dl=1 mm along the arc of radius r about the center O. (c) The maximum width of the source slit at which the fringe pattern on the screen can still be observed sufficiently sharp.

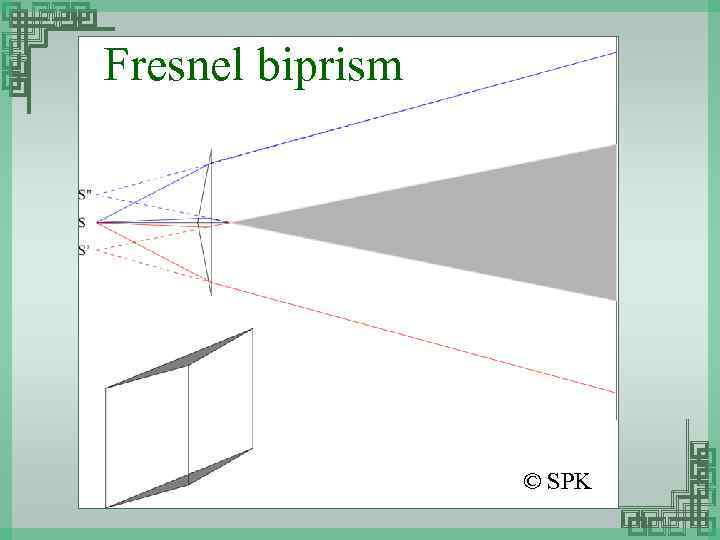Fresnel biprism © SPK Fresnel biprism © SPK

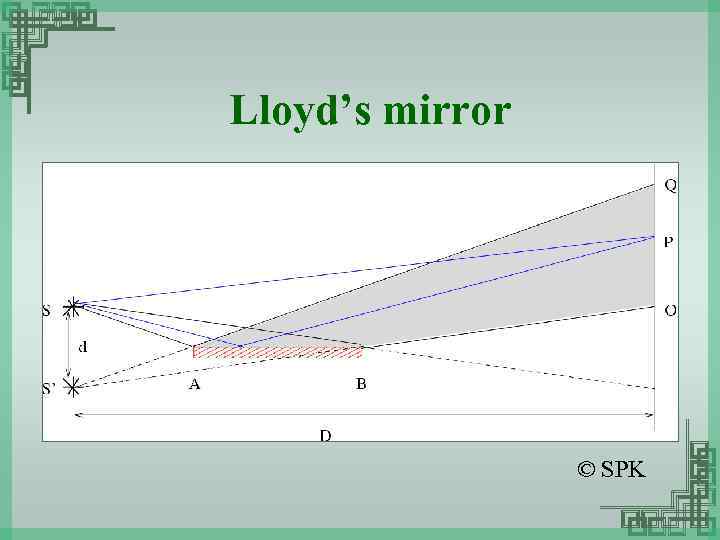Lloyd’s mirror © SPK Lloyd’s mirror © SPK

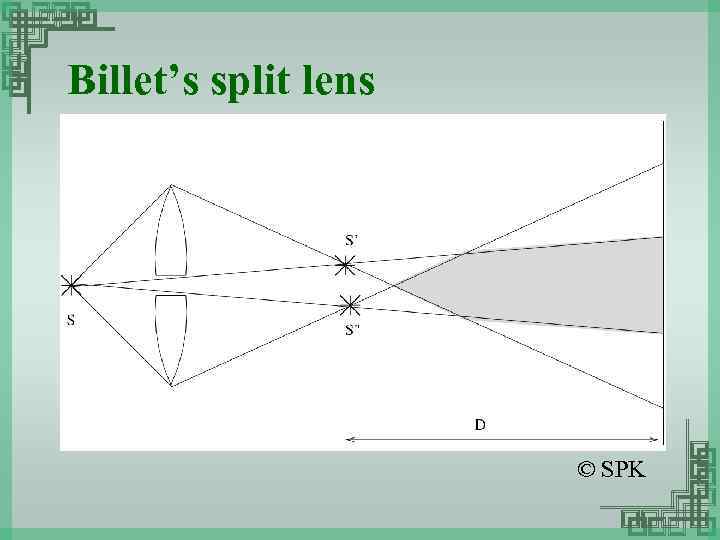Billet’s split lens © SPK Billet’s split lens © SPK

Wavefront splitting interferometers • Young’s double slit • Fresnel double mirror • Fresnel double Wavefront splitting interferometers • Young’s double slit • Fresnel double mirror • Fresnel double prism • Lloyd’s mirror

Division of Amplitude Division of Amplitude

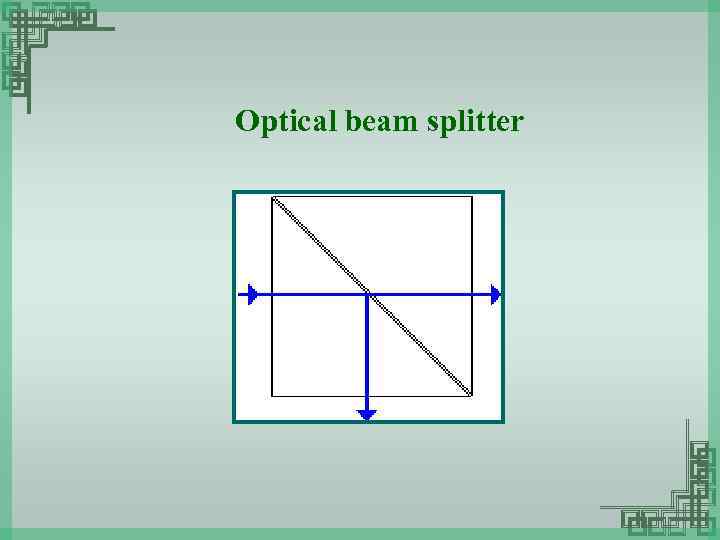Optical beam splitter Optical beam splitter

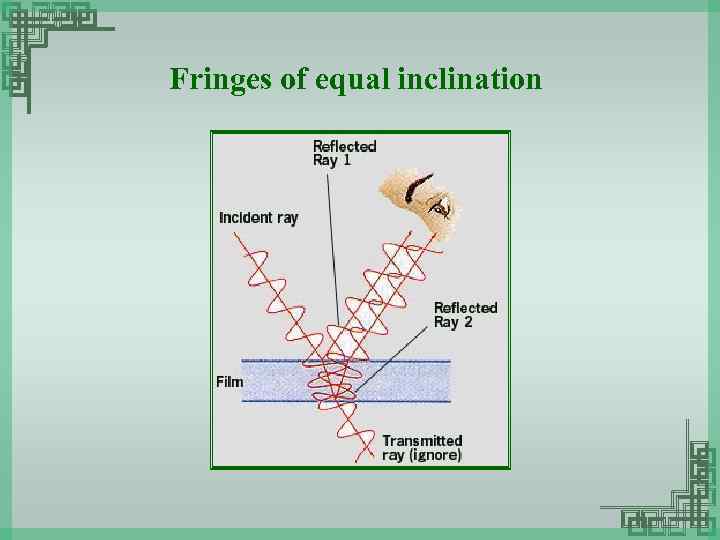Fringes of equal inclination Fringes of equal inclination

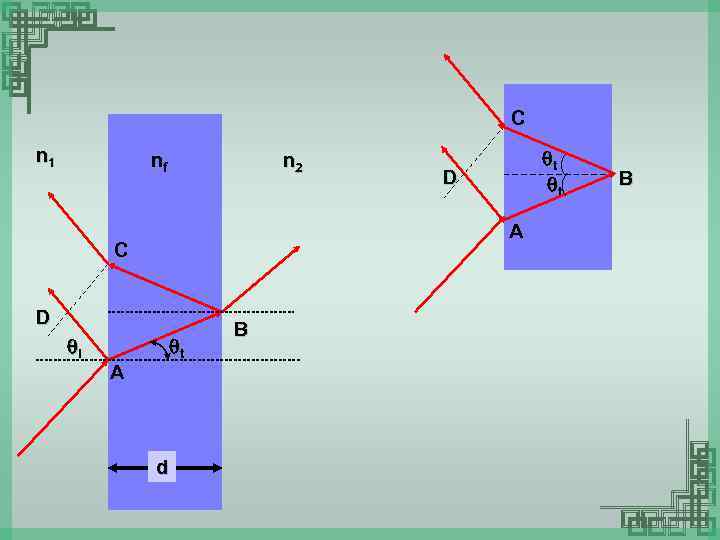C n 1 nf n 2 D A C D i t t t C n 1 nf n 2 D A C D i t t t A d B B

Optical path difference for the first two reflected beams Optical path difference for the first two reflected beams

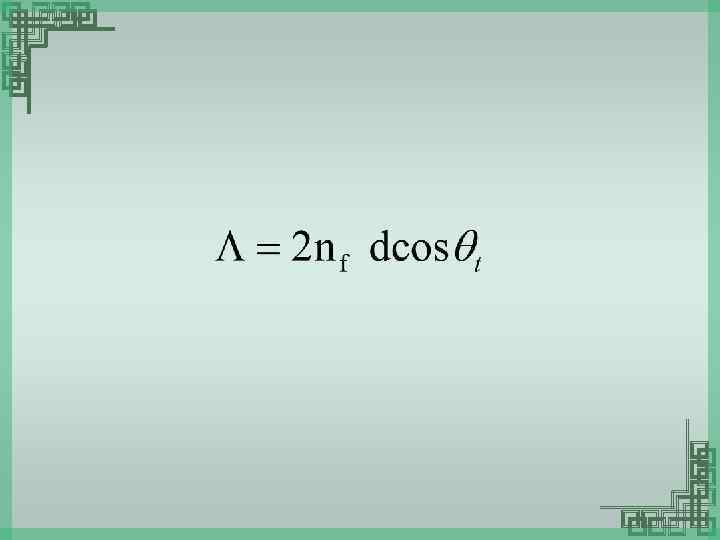
Condition for maxima Condition for minima Condition for maxima Condition for minima

Fringes of equal thickness Constant height contour of a topographial map Fringes of equal thickness Constant height contour of a topographial map

Wedge between two plates 1 2 glass t x Path difference = 2 t Wedge between two plates 1 2 glass t x Path difference = 2 t Phase difference = 2 kt - D air (phase change for 2, but not for 1) Maxima 2 t = (m + ½) o/n Minima 2 t = m o/n Fizeau Fringes

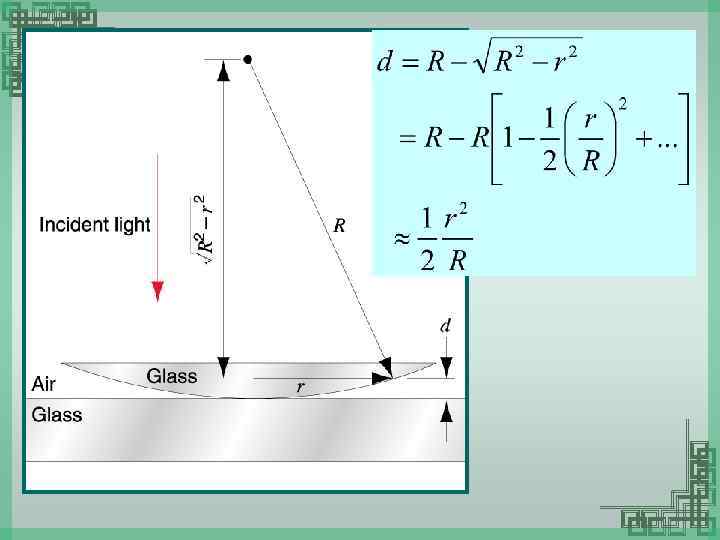
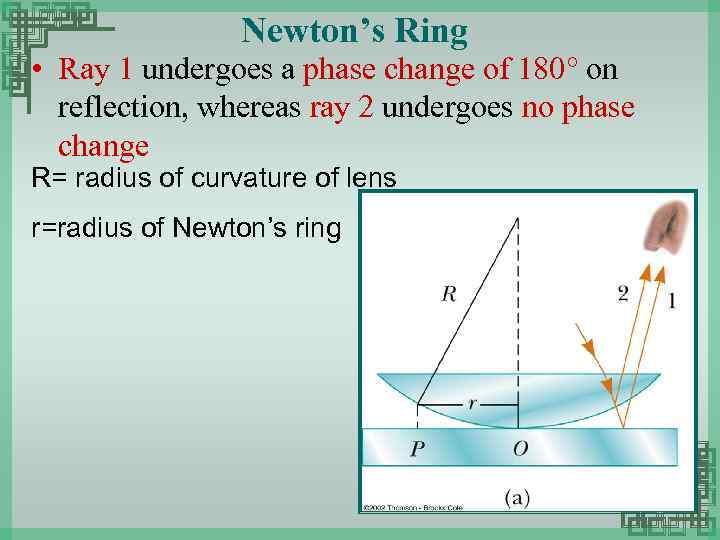Newton’s Ring • Ray 1 undergoes a phase change of 180 on reflection, whereas Newton’s Ring • Ray 1 undergoes a phase change of 180 on reflection, whereas ray 2 undergoes no phase change R= radius of curvature of lens r=radius of Newton’s ring

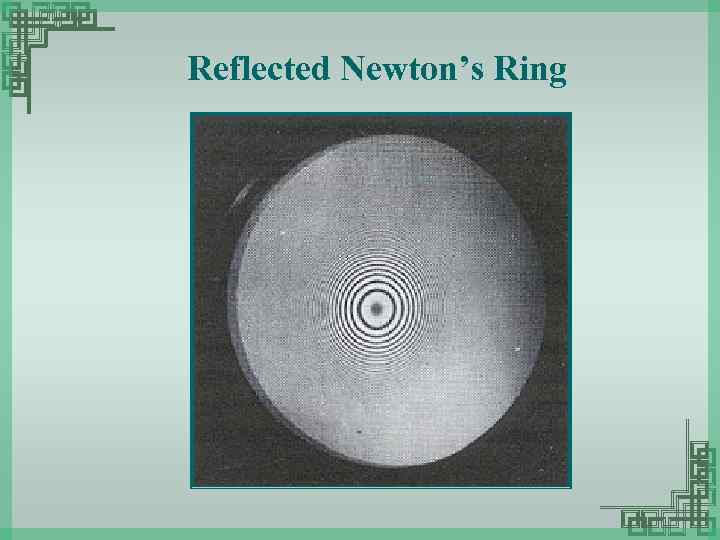Reflected Newton’s Ring Reflected Newton’s Ring

Newton’s Ring 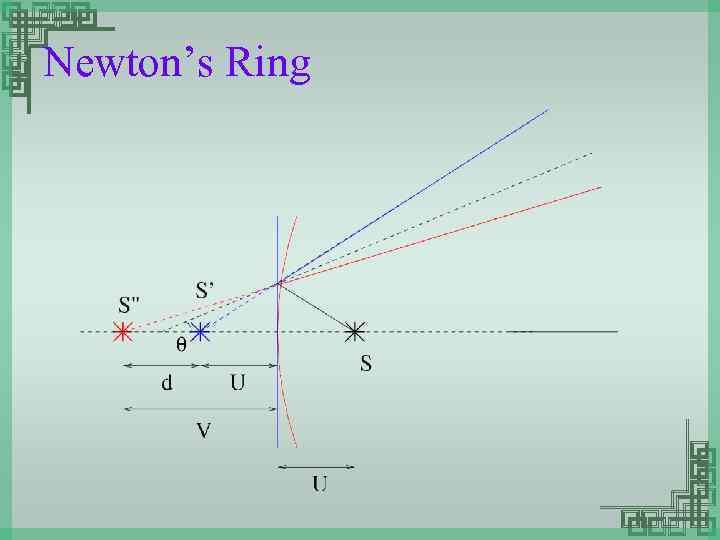Newton’s Ring

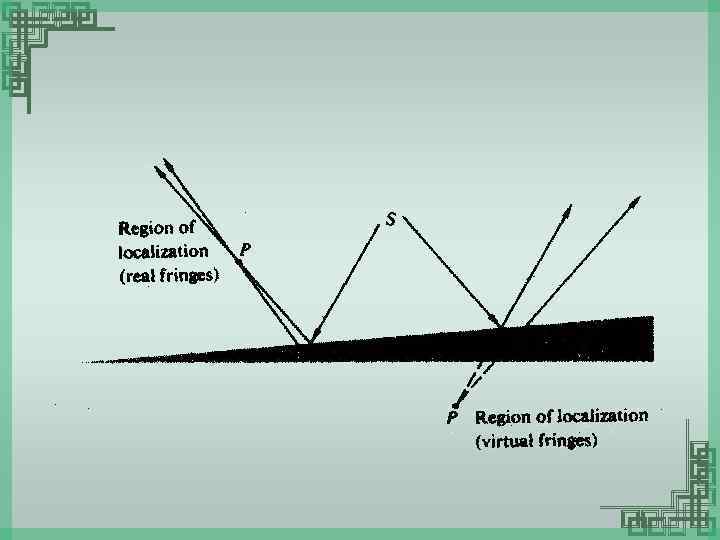
Types of localization of fringes Types of localization of fringes

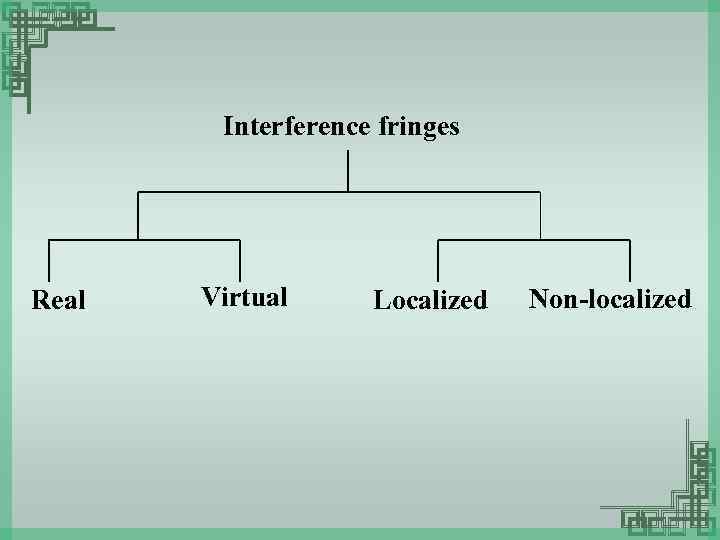Interference fringes Real Virtual Localized Non-localized Interference fringes Real Virtual Localized Non-localized

Localized fringe ØObserved over particular surface ØResult of extended source Localized fringe ØObserved over particular surface ØResult of extended source

Non-localized fringe ØExists everywhere ØResult of point/line source Non-localized fringe ØExists everywhere ØResult of point/line source

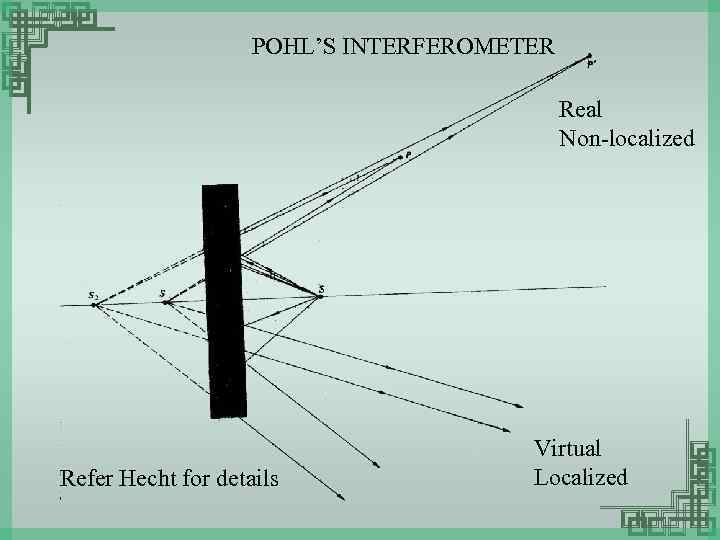POHL’S INTERFEROMETER Real Non-localized Refer Hecht for details Virtual Localized POHL’S INTERFEROMETER Real Non-localized Refer Hecht for details Virtual Localized

Problem The width of a certain spectral line at 500 nm is 2× 10 Problem The width of a certain spectral line at 500 nm is 2× 10 -2 nm. Approximately what is the largest path difference for which the interference fringes produces by the light are clearly visible?