Coding for DNA Computing Combinatorial and Biophysical Aspects

Coding for DNA Computing: Combinatorial and Biophysical Aspects Olgica Milenkovic University of Colorado, Boulder A Joint Work with Navin Kashyap Queen’s University, Kingston

LDPC ITERATIVE DECODING

Outline n The DNA Computing Paradigm n Applications n Error-Control Coding for DNA Computing n Constrained Coding: DNA Secondary and Tertiary Structure n Statistical Mechanics of DNA/RNA Folding n Results and Open Problems

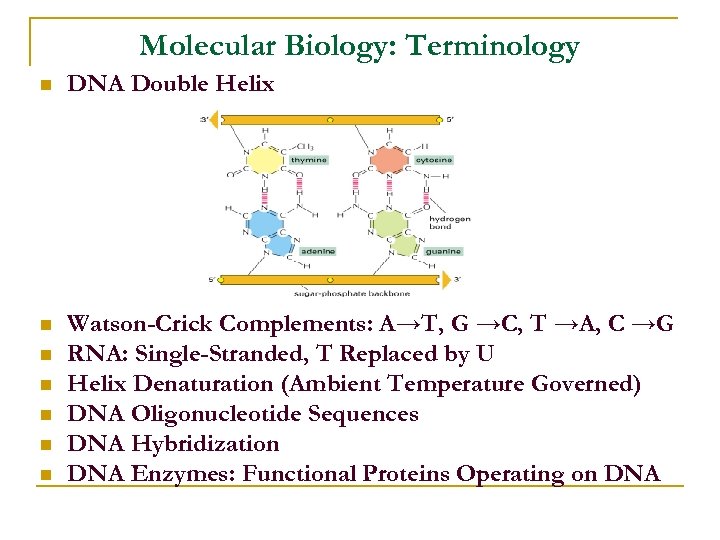
Molecular Biology: Terminology n DNA Double Helix n Watson-Crick Complements: A→T, G →C, T →A, C →G RNA: Single-Stranded, T Replaced by U Helix Denaturation (Ambient Temperature Governed) DNA Oligonucleotide Sequences DNA Hybridization DNA Enzymes: Functional Proteins Operating on DNA n n n

DNA Computing: Adleman’s Experiment (1994) The Problem: An “Unremarkable” Instance of the Directed Traveling Salesmen Problem on a Graph with Seven Nodes Figures from Adleman, SA 1998 The Method: Remarkable Oligonucleotide DNA Hybridization Technique Miami (CTACGG) NY (ATGCCG) Route (Edge): Second Half of Codeword for Miami (CGG) and First Half of Codeword for NY (ATG): CGGATG --- Take the Complement of this Word: GCCTAC

DNA Computing: The Benefits n n n n Not a von Neumann Architecture: Stochastic Mechanism with Massive Parallelism: 1/50 th of Teaspoon, 1014 paths/1 s Extremely Low Power Consumption: 1 Joule for 2 · 1019 Operations Storage Capacity: Vol(1 g of DNA)=1 cm 3 , Information=1 trillion CDs 18 Mb/inch of Length (0. 35 nm Between Base Pairs) Versatility of Applications, Only Plausible Option in Many Cases Drawbacks: First Implementations not Interactive 3 -Day Processing Delay VERY LOW RELIABILITY OF COMPUTATION

Applications of DNA Computers n n n Combinatorial Problems: Directed Traveling Salesmen (Adleman ‘ 94) 3 -SAT (Braich et. al. , ‘ 02) Figure Input: a 20 -Variable, 24 -Clause, Boolean Function 3 -Conjunctive Normal Form (3 -CNF) For each Variable, two Length=15 DNA Sequences Assigned, one representing the Variable, the other representing its Complement Operon Technology, Alameda, CA, Integrated DNA Technologies, Skokie, IL n Non-Attacking Knights (Faulhammer, ’ 00) Configurations of Knights that can be Placed on n×n Chess Board so that no Knight is Attacking any other Knight on the Board

Novel Designs of DNA Computers n DNA Logic and Automata: Interactive Systems n DNA Transistors (Stojanovic, Stefanovic ‘ 03) DNA Game-Playing Machines (Stojanovic, Stefanovic ‘ 03) MAYA: Consists of Nine Wells (Tubes) Representing the 3 x 3 Tic-Tac-Toe Board Tubes Contain Mixtures of Enzymes: Network of 23 Molecular Logic Gates “Human Player” has Nine Different DNA Strands: each Specific to one Square on the Board; Player Selects one Square to Play: DNA Strand representing that Square gets Added to all the Nine Wells; n O MAYA “Analyzes” Play Through Biochemical Reactions Occurring in Wells

Applications of DNA Computers n Meet MAYA…(Stojanovic, Stefanovic 2003) Figure: http: //www. cs. unm. edu/~bandrews/ttt-applet/

Applications of DNA Computers n The “Killer Application”: SMART DRUGS E. Shapiro et. al. (Weizmann Institute, Israel), Nature, Science 2003 Quintana et. al 2002 In Vitro DNA-Based Computer “Programmed” to Diagnose Cancer and “Order” Self. Destruction of Cells Identifies RNA Cancer Fingerprint Molecules Cancer Leaves its own “Chemical Fingerprint” in the Body, Including Over-Producing or Under-Producing Specific RNA Sequences (Analysis Based on Regulatory Networks of Gene Interactions, Shmulevich et. al. , 2002) (Milenkovic and Vasic, DIMACS’ 2004, ITW’ 2004) Software: DNA, Hardware: DNA Enzymes Responds Appropriately by Releasing Short, Active DNA Strand Interferes with Tumors by Suppressing Key Cancer Genes, Making Diseased Cells Self. Destruct Experiments: Prostate and Lung Cancer Cells

Applications of DNA Computers n Sensing, Storing, Nano-Scale Mechanics… n Biosensing: DNA Fingerprinting of Bacteria/Viruses, Roco et. al. 2004 DNA-Based Storage Systems: Mansuripur et. al. , DIMACS’ 2004 n n Nucleic Acid Nanostructures and Topology, DNA Self-Assembly, DNA Nanoscale Mechanical Devices, Seeman et. al. 1998 -2002 RELIABILITY ISSUES FOR ALL DESCRIBED SYSTEMS UNRESOLVED Error Control Coding Constrained Coding Graph Theory/Combinatorics/Pseudo-Knot Theory Statistical Mechanics

The Biggest Obstacles… n n DNA Oligonucleotide Secondary and Tertiary Structure Formation Unwanted Hybridization DNA Oligonucleotide Sequences are Chemically Active, Tend to Assume Thermodynamically Most Stable Form! DNA Sequences can Bind to Partially Complementary Sequences as Well!

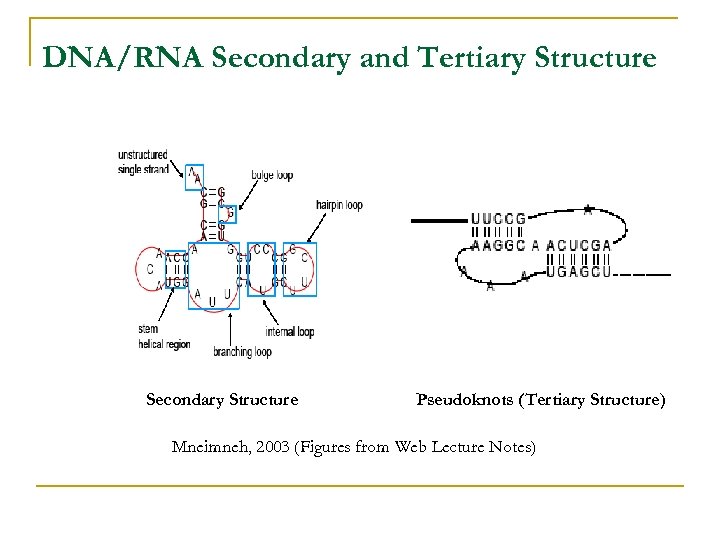
DNA/RNA Secondary and Tertiary Structure Secondary Structure Pseudoknots (Tertiary Structure) Mneimneh, 2003 (Figures from Web Lecture Notes)

DNA Hairpins DNA/RNA Hairpin Structure Participate in Important Biological Functions: • Regulation of Gene Expression (Zazopoulos, et. al. , 1997); • DNA Recombination (Froelich-Ammon, et. al. , 1994); • Facilitation of Mutagenic Events (Trinh and Sinden, 1993): in Living Cell, after Breaking of Intermolecular Pairing in Double Helix DNA, Loose Strands Form a DNA Hairpin; • Potential Antisense Drug (Tang, et. al. , 1993): Injecting into a Living Cell Hairpin with Nucleic Acid Bases Complementary to an m. RNA of a Disease Gene Blocks its Expression

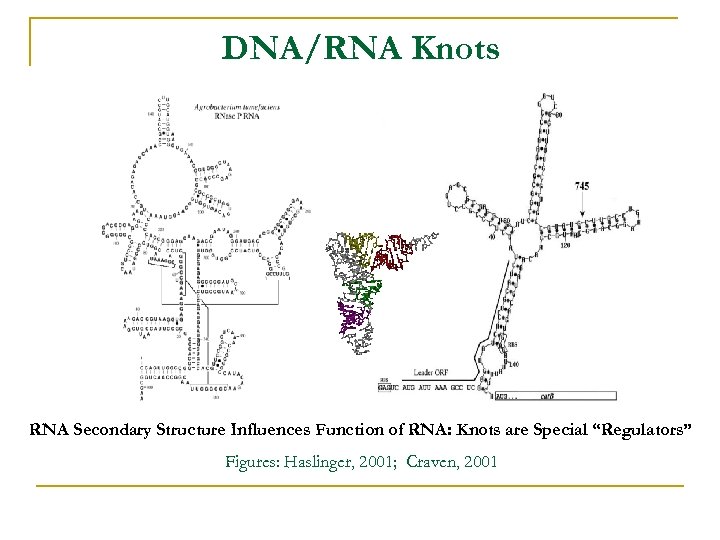
DNA/RNA Knots RNA Secondary Structure Influences Function of RNA: Knots are Special “Regulators” Figures: Haslinger, 2001; Craven, 2001

Mathematical Formulation Definition 1 (Hasliner, 2001): A Secondary Structure S is a Vertex-Labeled Graph on n Vertices, for which the Adjacency Matrix A has the following properties An Edge (i, j), |i-j|>1 is Called a Base-Pairing. A Secondary Structure Can Consist of the Following Structural Elements: 1. A Stack Consists of Subsequent Base Pairs (p-k, q+k), 2. (p-k+1, q+k-1), …, (p, q); k is the Length of the Stack 2. A Loop Consists of all Unpaired Vertices which are Immediately Interior to some Terminal Base Pair 3. An External Vertex is an Unpaired Vertex which does not Belong to a Loop

Mathematical Formulation If Definition 1, Part 3 is Violated for a Base Pairing, then the Resulting Formation is Referred to as a Pseudoknot n n With Information about Energy of Pairings and Additional Measurements Regarding the DNA Backbone, Determining Stable Secondary Structures Becomes a Purely Combinatorial Problem n Secondary Structure Prediction: Dynamical Programming Approach, Polynomial Time Nussinov’s and Zuckermann Algorithm n Pseudoknots: NP-Complete, Except for Special Class of H-Knots (Rivas, Eddy 2003)

Nussinov’s Folding Algorithm Free Energy of Secondary Structure S : Free Energy of Secondary Structure Limited to positions i, i+1, …, j Figure: Mneimneh, 2003, Bundschuh, 2004 Feynman Diagrams for RNA Structure Prediction (Eddy, Rivas 2001) Free Energy Table: Sequence CCCAAATGG

Statistical Physics: DNA Ensemble Analysis Bundschuh, Hwa 2004: Statistics of Secondary Structures in Ensemble of Long Random DNA Sequences Why? Detection of Important Structural Components in m. RNAs, Functional RNAs, Characterization of the Response of Long Oligonucleotide DNA Molecule to Puling Forces Random DNA = Problem of Disordered Systems Bundschuh, Hwa 2004

Statistical Physics: DNA Ensemble Analysis n Molten Phase: Absence of Disorder Thermodynamic Ensemble: Large Number of Different Secondary Structures with Equal Energy Stability of Molten Phase: Use N-Replica Method

Stat Physics DNA Ensemble Analysis n Glassy Phase: Few Low Energy Configurations in Thermodynamic Limit Droplet Theory (Huse and Fisher): ‘‘Large-Scale Low-Energy Excitations’’ About Ground State • Impose deformation over a length scale L>>1, Monitor Minimal Free Energy Cost of Deformation; • Cost Expected to Scale as Lw for large L: Positive w Indicates Deformation Cost Grows with Increasing Size. Negative w Indicates Deformation Cost Decays: there is a Large Number of Configurations with Low Overlap with Ground State, whose Energies are Similar to the Ground State Energy in the Thermodynamic Limit (Zero-Temperature Behavior not Stable to Thermal Fluctuations - No Thermodynamic Glass Phase can Exist at any Finite Temperature Related Analysis: A. Pagnani. G. Parisi and F. Ricci, , Tersenghi , 2000/2001

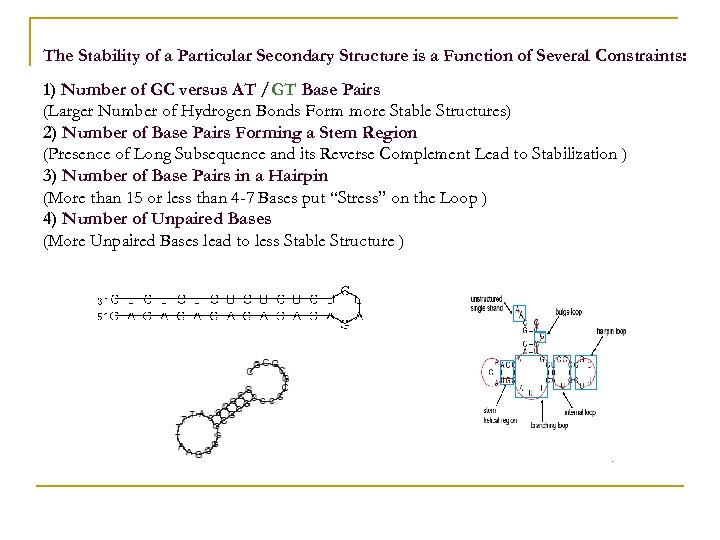
The Stability of a Particular Secondary Structure is a Function of Several Constraints: 1) Number of GC versus AT /GT Base Pairs (Larger Number of Hydrogen Bonds Form more Stable Structures) 2) Number of Base Pairs Forming a Stem Region (Presence of Long Subsequence and its Reverse Complement Lead to Stabilization ) 3) Number of Base Pairs in a Hairpin (More than 15 or less than 4 -7 Bases put “Stress” on the Loop ) 4) Number of Unpaired Bases (More Unpaired Bases lead to less Stable Structure )

Hybridization Constraints n Individual Sequence Constraints (Wood, Tsaftaaris etc): IP 1) The consecutive-bases constraint. Long Runs of the Same Base Forbidden. IP 2) The constant GC-content constraint. Introduced to Achieve Parallelized Operations on DNA Sequences; Assures Similar Thermodynamic (Melting Temperature) Characteristics of all Codewords. GC-Content Usually in the Range of 30 -50% of Code Length; n Joint Sequence Constraints: JP 1) The Hamming distance constraint. Limits Unwanted Hybridizations between Codewords. Requirement is that all Distinct Pairs of Codewords p, q in C be at Hamming Distance at Least dmin. To Limit Undesired Hybridization between a Codeword and the Reverse. Complement of any other Codeword (including itself) the Reverse Complement Hamming Distance has to be at Least d. RCmin JP 2) The frame-shift constraint. Applies Only to Limited Number of Problems. Refers to Requirement that Concatenation of Two or More Codewords should not Properly Contain Another Codeword. JP 3) The forbidden subsequence constraint. Specifies that a Class of Substrings Must not Occur in any Codeword or Concatenation of Codewords

Code Construction PRIOR WORK: Addressed 1/2/3 Requirements; No Families of Codes Given (Length Limited to 20); No Attempt Whatsoever to Consider Secondary Structure Constraints; References: Condon et. al. 2000 -2004; King 2003; Ryakov 2003; Gaborit and King 2004; Ghrayeb et. al. 2004; n n Approach I: Binary Mapping Approach II: Extended, Cyclic Goppa Codes over GF(4) Approach III: Hadamard Matrices with Cyclic Core WHY Cyclic? Will Show that Computational Complexity for Nussinov’s Algorithm Significantly Reduced in this Case

Terminology DNA Code C : Set of Codewords over Alphabet Q; Minimum Hamming, Reverse and Reverse-Complement Hamming Distance: Constant GC Content Code:

Binary Mapping Approach Example: q=ACGTCC b(q)=001011011010 e(q)=011011 o(q)=001100 Code D: [n, k, d], Contains All-Ones Word Construction: DNA Code: Number of Codewords Length 2 n Hamming, Reverse Complement Hamming Distance at Least d

Longest Length Codes… Bounds on (Based on Bounds by Ashikhmin et al, 2005) Binary Mapping: Subcodes of Simplex Codes (All-Zero Not Allowed) -- EVEN Special Subset of Codewords from Menas/Zettenberg Codes --ODD

Approach: Extended Cyclic Goppa Codes • Take a Family of Reversible ( ) Cyclic Codes • Eliminate all Self-Reversible Codewords • From Each Remaining Pair Retain Exactly One Codeword • Complement Second Half of Each Codeword Let for q a Power of a Prime and over such that g(z) has no Root in. The Goppa Code, , consists of all words is a code of length n, dimension Zhang et. al. , 1988 Let g(z) be a Polynomial of Degree such that and minimum distance .

DNA Codes and Goppa Codes self-reversible A Reversible Cyclic Code of Dimension k over GF(q) contains Codewords. For arbitrary positive integers a, m, there exist DNA Codes D such that having the following properties Choose Constant GC Content Subset of Codewords Example: CGTTC, CAAAT, CTCCA, GCCTT, GGAGA, ACTAA

Dimension n×n over Set m-th Roots of Unity Complexof(Generalized)of. Hadamard Matrices Matrix With property Exponent Matrix: over Theorem[Heng et. al, 02] Let N=pk-1 for p Prime and a Positive Integer k. Let g(x)=c 0+c 1 x+c 2 x 2+…+c. N-kx. N-k be a Monic Polynomial over Zp, of Degree N-k, such that g(x)h(x)=x. N-1 over Zp , for some monic irreducible polynomial h(x) in Zp[x]. Suppose that the vector , (0, c 1, c 2, …, c. N-k) with ci=0 for N-k<i<N has the property that it contains each element of Zp the same number of times. Then the N cyclic shifts of the vector (c 0, c 1, c 2, …, c. N-k) form the code of the exponent matrix of some Hadamard matrix H(pk, Cp) Choose p=3, and Use only One of G/C For any , there exists DNA codes D with constant GC-content equal to and codewords of length Each Codeword of such a Code is a Cyclic Shift of a Fixed Generator Codeword g. ,

Hadamard and Vienna… Vienna Package: T=37◦C http: //www. tbi. univie. ac. at/~ivo/RNA/ Based on Nussinov’s Algorithm Gives one Minimum Free Energy Secondary Structure MFOLD (Zuckerman et. al. 2000)

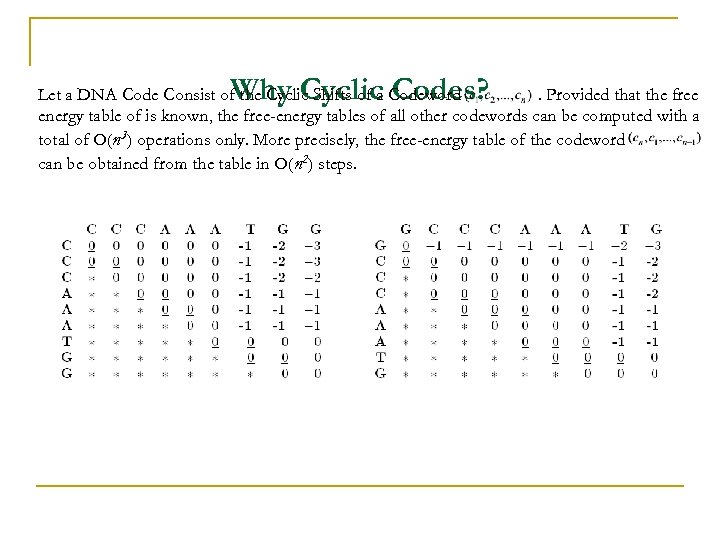
Why Cyclic Codes? Let a DNA Code Consist of the Cyclic Shifts of a Codeword. Provided that the free energy table of is known, the free-energy tables of all other codewords can be computed with a total of O(n 3) operations only. More precisely, the free-energy table of the codeword can be obtained from the table in O(n 2) steps.

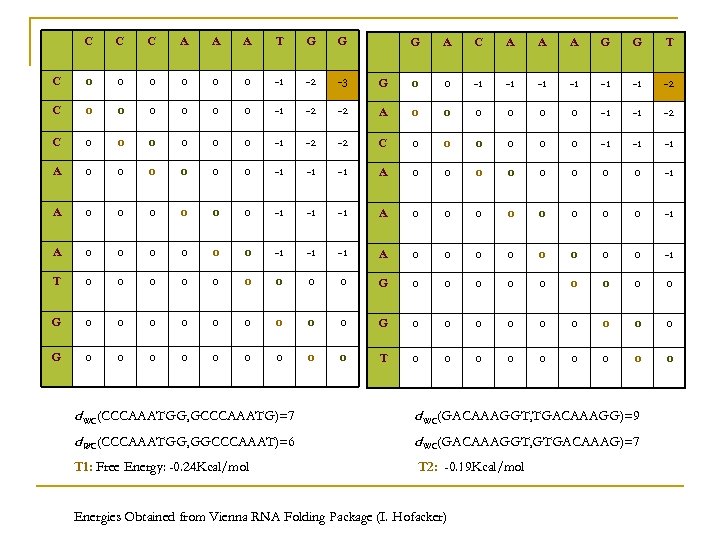
C C C A A A T G G C 0 0 0 -1 -2 -3 C 0 0 0 -1 -2 C 0 0 0 -1 A 0 0 0 A 0 0 T 0 0 0 G A C A A A G G T G 0 0 -1 -1 -1 -2 -2 A 0 0 0 -1 -1 -2 -2 -2 C 0 0 0 -1 -1 -1 A 0 0 0 0 -1 -1 -1 A 0 0 0 0 -1 0 0 0 G 0 0 0 0 0 0 0 T 0 0 0 0 0 d WC(CCCAAATGG, GCCCAAATG)=7 d WC(GACAAAGGT, TGACAAAGG)=9 d WC(CCCAAATGG, GGCCCAAAT)=6 d WC(GACAAAGGT, GTGACAAAG)=7 T 1: Free Energy: -0. 24 Kcal/mol T 2: -0. 19 Kcal/mol Energies Obtained from Vienna RNA Folding Package (I. Hofacker)

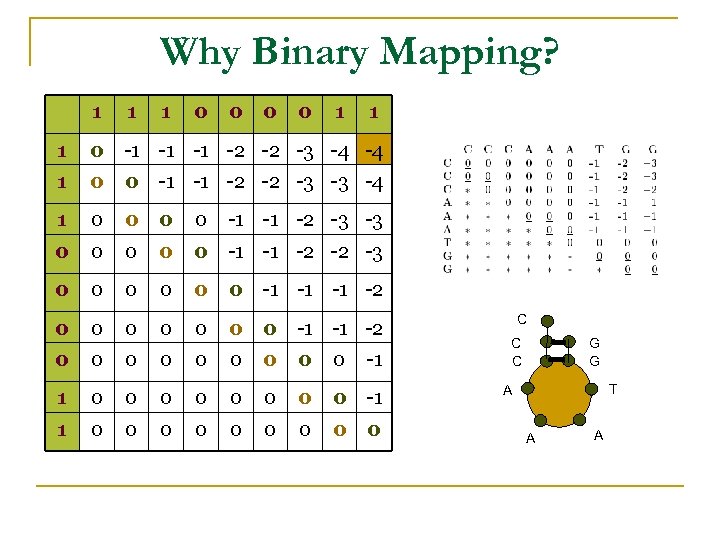
Why Binary Mapping? 1 1 1 0 0 1 1 1 0 -1 -1 -1 -2 -2 -3 -4 -4 1 0 0 -1 -1 -2 -2 -3 -3 -4 1 0 0 0 0 0 -1 -1 -2 -2 -3 0 0 0 -1 -1 -1 -2 0 0 0 0 0 1 0 0 0 0 -1 -1 -2 -3 -3 -1 0 C C C G G T A A A

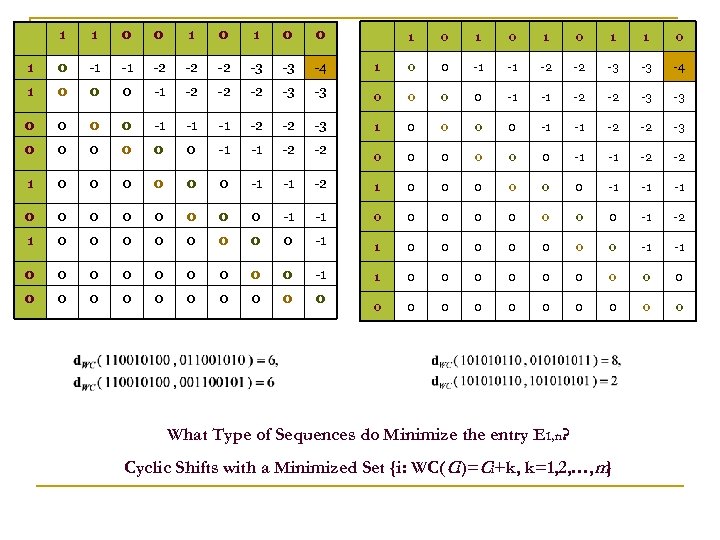
1 1 0 0 1 0 -1 -1 -2 -2 -2 -3 -3 -4 1 0 0 0 -1 -2 -2 -2 -3 0 0 -1 -1 -1 -2 0 0 0 -1 1 0 0 0 0 0 1 0 1 1 0 0 -1 -1 -2 -2 -3 -3 -4 -3 0 0 -1 -1 -2 -2 -3 -3 -2 -3 1 0 0 -1 -1 -2 -2 -3 -1 -2 -2 0 0 0 -1 -1 -2 -2 0 -1 -1 -2 1 0 0 0 -1 -1 -1 0 0 0 -1 -2 0 0 0 -1 1 0 0 0 0 -1 -1 0 0 0 -1 1 0 0 0 0 0 0 0 What Type of Sequences do Minimize the entry E 1, n? Cyclic Shifts with a Minimized Set {i: WC(Ci)=Ci+k, k=1, 2, …, m}

The Cyclic Distance (Binary Case) n Known: Peng, 1998 Sequence Weight: w =n/2, n even w =(n-1)/2, n odd Achieved: Maximum Length Shift Register (MLSR) Sequences (Pseudo-Random Sequences in General) What are the Reversal Distance Properties of MLSR Sequences?

The Watson-Crick Distance n Watson-Crick Distance: Plotkin-Type of Bound

The Free Energy of a DNA Strand (c 1, c 2, …, cn) can be Approximated According to Breslauer’s Formula Much more Accurate:

Other Coding Problems n n n Generalized de. Bruijn Sequences Association Schemes for Hamming/RC Hamming/Constant GC Content Binary Mapping Approach with Runlength Constraints Forbidden Pattern Constraints (Enumeration Techniques by Goulden and Jackson…) Catalan Numbers: b=1: CN(1)=1 ( ) b=2: CN(2)=2 ( ), ( ( ) ) b=3: CN(3)=5 ( ) ( ), ( ( ) ) ( ), ( ) ( ( ) ), ( ( ( ) ) )