Coalgebraic components in a many-sorted microcosm Ichiro Hasuo

Coalgebraic components in a many-sorted microcosm Ichiro Hasuo Chris Heunen Kyoto, JP Nijmegen, NL ( Oxford, UK) Bart Jacobs Nijmegen, NL Ana Sokolova Salzburg, AT

Hughes’ arrow, Freyd category, … from functional programming Outline Universal coalgebra in CS components (state-based machines) as coalgebras their behaviors by final coalgebra as algebraic structure calculus on them compositionality results SOS by bialgebras The Microcosm Principle [Baez-Dolan][Hasuo-Jacobs-Sokolova, Fo. SSa. CS’ 08] what’s new: many-sorted, pseudo algebra

Behavioral view on component calculi Part 1

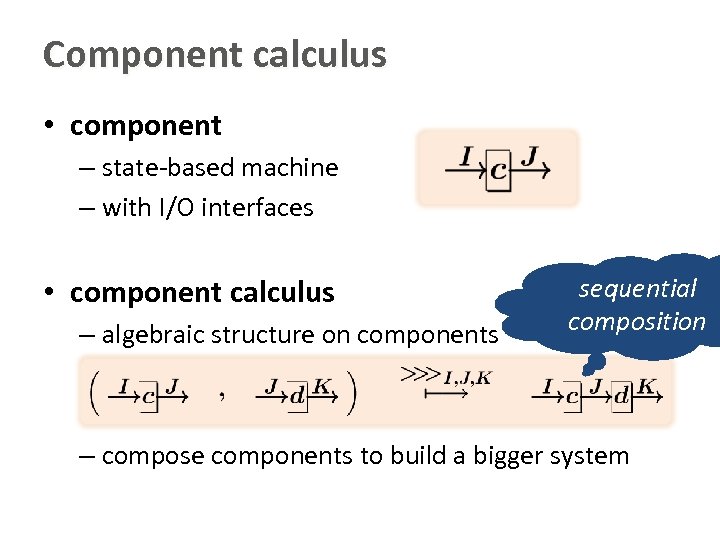
Component calculus • component – state-based machine – with I/O interfaces • component calculus – algebraic structure on components sequential composition – compose components to build a bigger system

Component calculus: background • Modular design – Against fast-growing complexity of systems – Brings order to otherwise messed-up design process • Middle-ware layer – You won’t code everything from scratch, but – buy software components from other vendors, – which you compose

Components as coalgebras [Barbosa, Ph. D thesis] I c in Sets as J T : a monad for effect (cf. func. programming) P (powerset) non-determinism 1+ _ exception (S £ _)S global state DX = { d: X [0, 1] | x d(x) = 1} probability

Component calculus = algebra on Coalg. F binary operation

Behavioral view Summary • component as coalgebra I c J • component calculus as algebra on Coalg. F • Behavior of components? – compositionality of calculus – coalgebraic view as

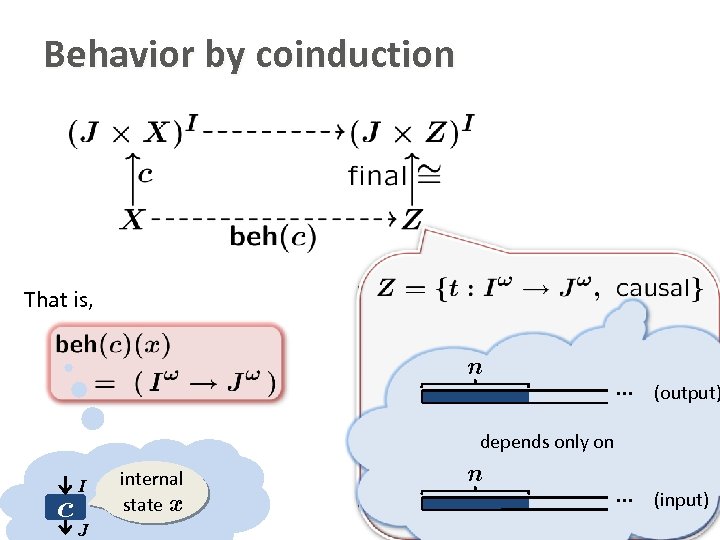
Behavior by coinduction That is, n … (output) … (input) depends only on c I J internal state x n

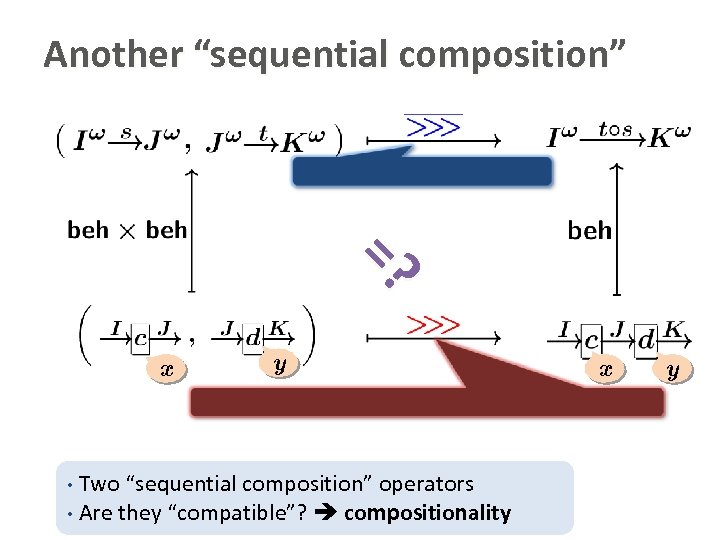
Another “sequential composition” =? =? x y Two “sequential composition” operators • Are they “compatible”? compositionality • x y

One arises from the other by coinduction definition principle

Compositionality = = • i. e. • by coinduction proof principle

Nested algebraic structure: the microcosm principle with X 2 C outer interpretation inner interpretation algebraic theory o operations binary o equations e. g. assoc. of

Microcosm in macrocosm We name this principle the microcosm principle , after theory, common in pre-modern correlative cosmologies, that every feature of the microcosm (e. g. the human soul) corresponds to some feature of the macrocosm. John Baez & James Dolan Higher-Dimensional Algebra III: n-Categories and the Algebra of Opetopes Adv. Math. 1998

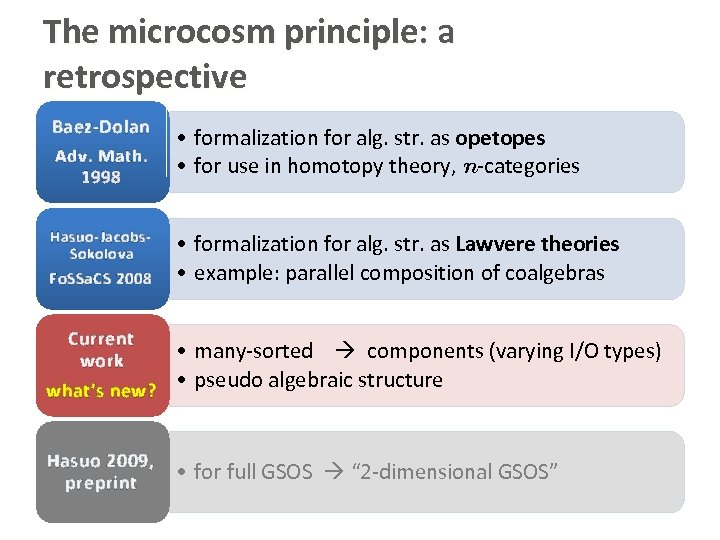
The microcosm principle: a retrospective Baez-Dolan Adv. Math. 1998 Hasuo-Jacobs. Sokolova Fo. SSa. CS 2008 • formalization for alg. str. as opetopes • for use in homotopy theory, n-categories • formalization for alg. str. as Lawvere theories • example: parallel composition of coalgebras Current work • many-sorted components (varying I/O types) • pseudo algebraic structure what’s new? Hasuo 2009, preprint • for full GSOS “ 2 -dimensional GSOS”

Main result: compositionality We study three component calculi: PLTh, Arr. Th, MArr. Th. For each of them: 1. We introduce algebraic structure on Coalg. F – such as 2. from which algebraic structure on Z canonically arises – – such as by coinduction (def. principle) 3. relating the two, we have the compositionality property – by coinduction (proof principle)

T h e m i c r o c o s m p r i n c i p l e Part 2

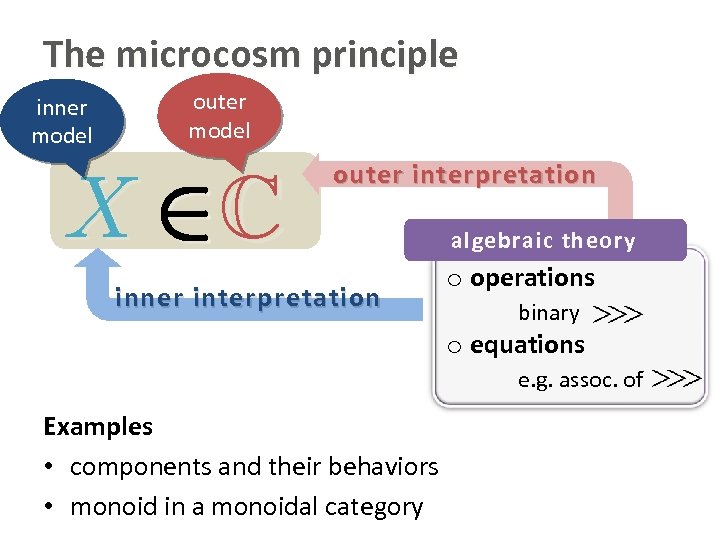
The microcosm principle inner model outer model X 2 C outer interpretation inner interpretation algebraic theory o operations binary o equations e. g. assoc. of Examples • components and their behaviors • monoid in a monoidal category

Microcosm principle in [Mac. Lane, CWM] monoid in a monoidal category • You may have seen it – “a monoid is in a monoidal category”

Lawvere theory L a category representing an algebraic theory

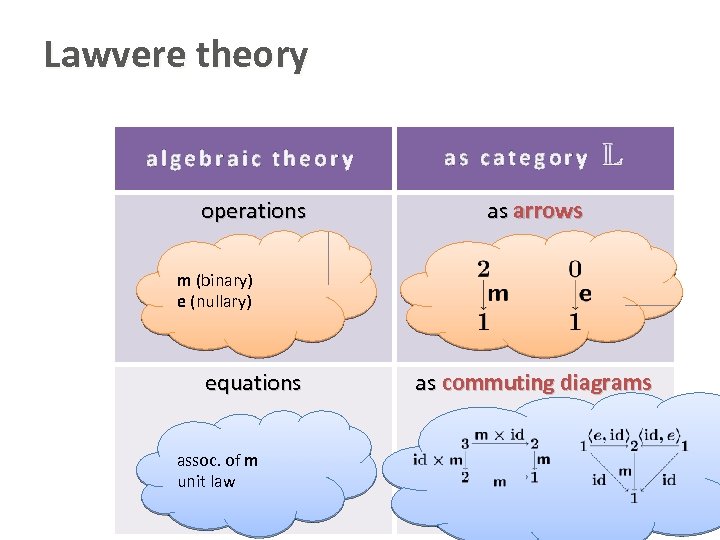
Lawvere theory algebraic theory operations as category L as arrows m (binary) e (nullary) equations assoc. of m unit law as commuting diagrams

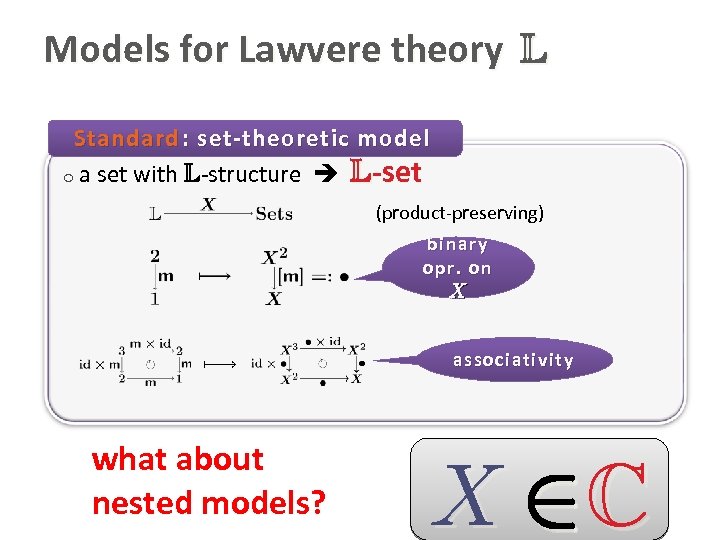
Models for Lawvere theory L Standard : set-theoretic model o a set with L-structure L-set (product-preserving) binary opr. on X associativity what about nested models? X 2 C

Outer model: L-category outer model o a category with L-structure: L-category (product-preserving) NB. This works only for strict algebraic structure

Inner model: L-object [cf. Benabou] Definition Given an L-category C, an L-object X in it is a lax natural transformation compatible with products. components inner alg. str. by mediating 2 -cells lax naturality X: carrier obj.

Compositionality theorem Assume ¡ ¡ ¡ C is an L-category F : C C is a lax L-functor there is a final coalgebra Z FZ 1. Coalg F is an L-category 2. Z FZ is an L-object 3. the behavior functor by coinduction is a (strict) L-functor

What’s new (1): many-sorted The specification: arity: formal product of sorts: (I, J), (J, K), etc. one-sorted case:

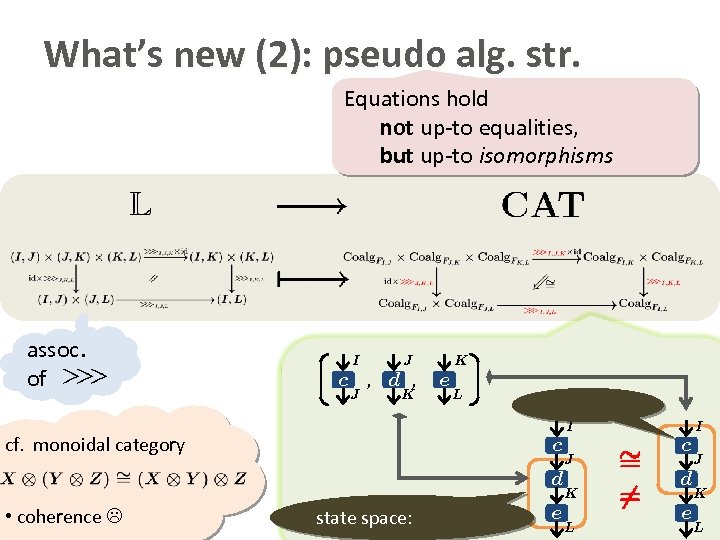
What’s new (2): pseudo alg. str. Equations hold not up-to equalities, but up-to isomorphisms assoc. of I J c , d , J K K e L I cf. monoidal category c d • coherence state space: e J K L I c d e J K L

Functorial semantics outer model o a category with L-structure: L-category (product-preserving) NB. This works only for strict algebraic structure

Formalizing pseudo alg. str. • Lawvere 2 -theory [Power, Lack] – explicit isomorphisms, explicit coherence • theory of monoids: • theory of monoidal categories : – “ 2 -functorial semantics” • model = category with L-structure • it is a product-preserving 2 -functor – not quite a suitable solution for us… L CAT

Formalizing pseudo alg. str. • Pseudo functorial semantics Hasuo, preprint 2009 available on the web Definition An L-category is a finite-product preserving pseudo functor L CAT – Segal took the same approach in TQFT, topological quantum field theory • but for monoidal (not cartesian/Lawvere) theory L

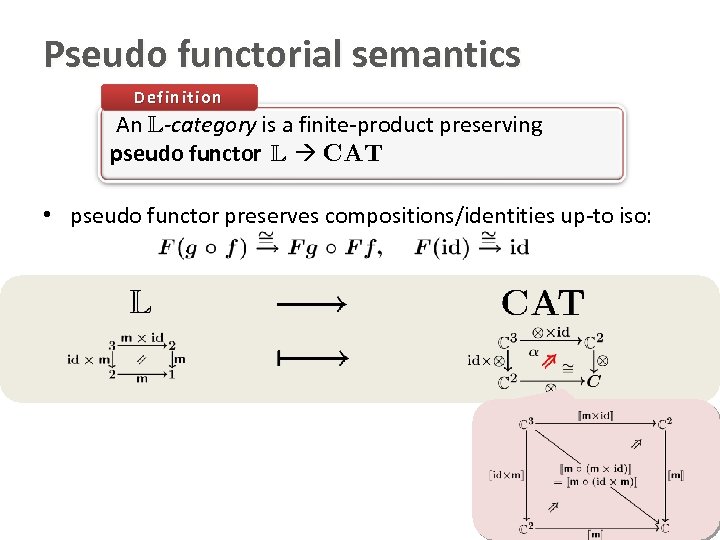
Pseudo functorial semantics Definition An L-category is a finite-product preserving pseudo functor L CAT • pseudo functor preserves compositions/identities up-to iso:

Pseudo functorial semantics Definition An L-category is a finite-product preserving pseudo functor L CAT subtle, needs fine-tuning natural, from an operadic point of view Theorem [Leinster]

Assume ¡ ¡ ¡ C is an L-category F : C C is a lax L-functor there is a final coalgebra Z FZ 1. Coalg F is an L-category 2. Z FZ is an L-object 3. the behavior functor by coinduction is a (strict) L-functor lifts Compositionality theorem again

compositionality r e s u l t s f o r component calculi Part 3

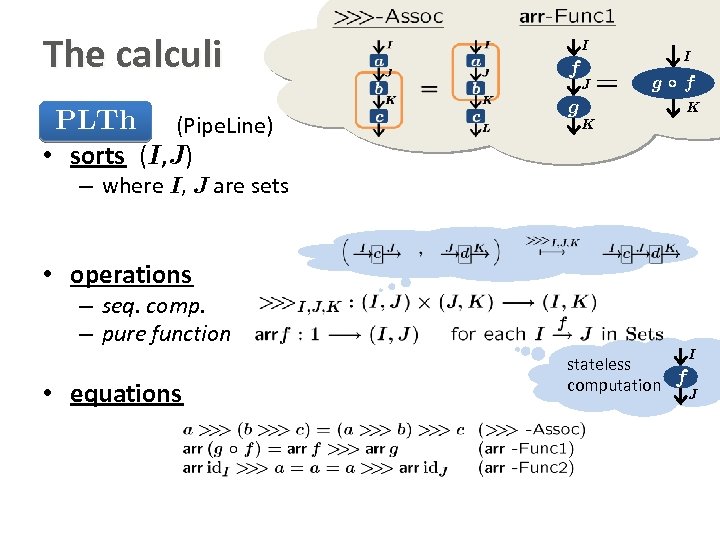
The calculi PLTh (Pipe. Line) • sorts (I, J) I f J g I g±f K K – where I, J are sets • operations – seq. comp. – pure function I • equations stateless computation f J

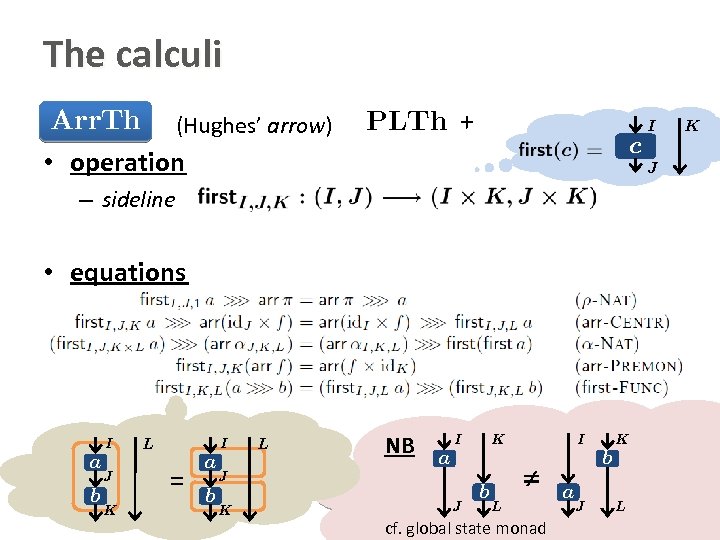
The calculi Arr. Th (Hughes’ arrow) PLTh + I c • operation J – sideline • equations I a b J K I L = a b L NB I a J K K J b I L cf. global state monad K b a J L K

The calculi PLTh (Pipe. Line) Arr. Th (Hughes’ arrow) = PLTh + first MArr. Th (Monoidal arrow) = PLTh + • operation – (synchronous) parallel composition • equations I c K d J L

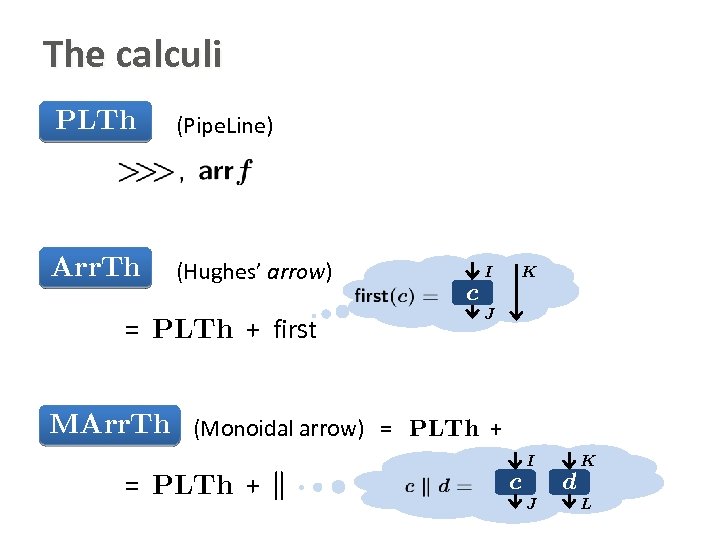
The calculi PLTh (Pipe. Line) Arr. Th (Hughes’ arrow) = PLTh + first I K c J MArr. Th (Monoidal arrow) = PLTh + k I c K d J L

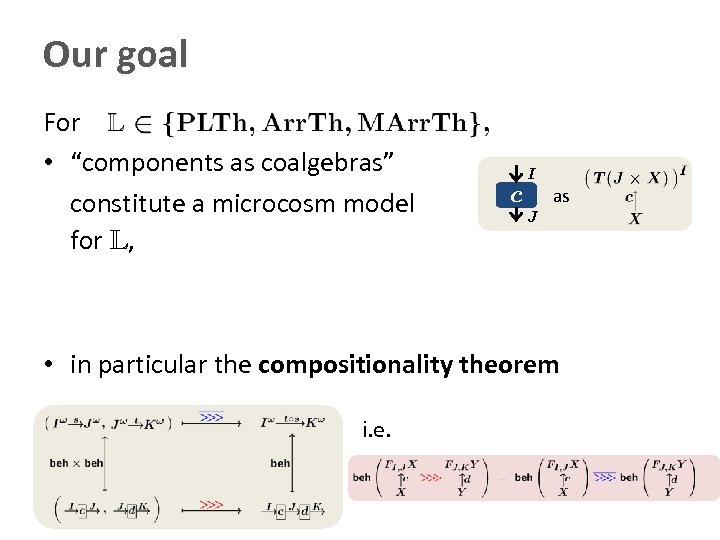
Our goal For • “components as coalgebras” constitute a microcosm model for L, I c as J • in particular the compositionality theorem i. e.

BTW, in functional programming… • Kleisli category Kl(T) – given a monad T for effect – the category of T-effectful computations: • The “hom-model” Theorem [Power-Robinson] 1. Kl(T) is a (set-theoretic) model of PLTh arrow [Hughes] Freyd category [Levy-Power-Thielecke] 2. T: strong Kl(T) is a model of Arr. Th 3. T: commutative Kl(T) is a model of MArr. Th “monoidal” arrow

Follow from these outer models: • inner models • compositionality I Categorification Theorem [Power-Robinson] c as J signature: Theorem • T: monad a model • T: strong monad • T: commutative monad

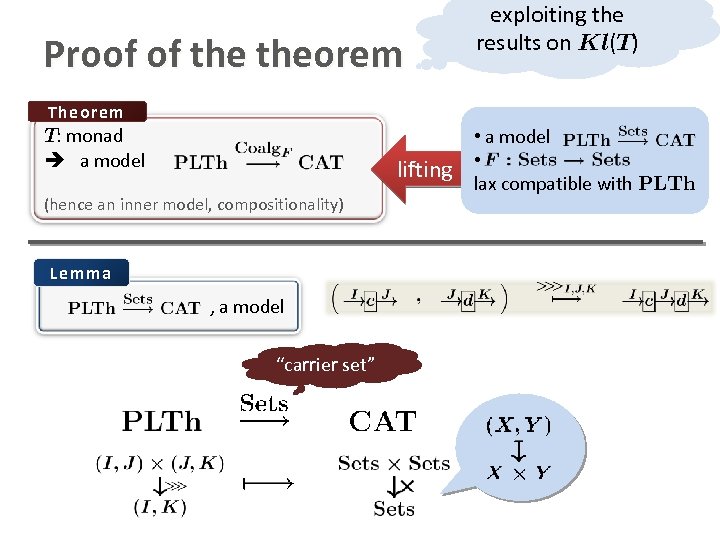
Proof of theorem exploiting the results on Kl(T) Theorem T: monad a model lifting (hence an inner model, compositionality) Lemma , a model “carrier set” • a model • lax compatible with PLTh

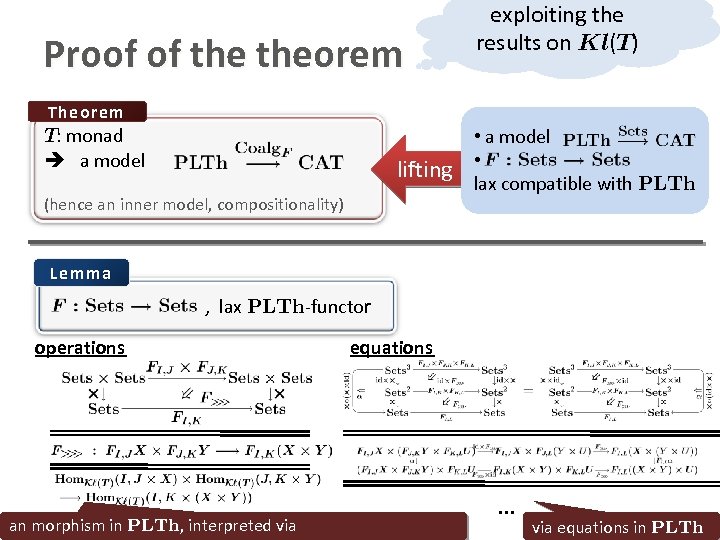
Proof of theorem exploiting the results on Kl(T) Theorem T: monad a model lifting (hence an inner model, compositionality) • a model • lax compatible with PLTh Lemma , lax PLTh-functor operations an morphism in PLTh, interpreted via equations … via equations in PLTh

Future work • Richer component calculi – feedback traced monoidal structure? – delayed/lossy channels different effect monad T ? • Other “algebra in algebra” – for component calculi: L-algebra in L-algebra – in general: L 1 -algebra in L 2 -algebra • usually: L 2 -algebra = “category with finite products” • Theory of generalized operads/combinatorial species [Leinster] [Fiore-Gambino-Hyland-Winskel] [Curien]

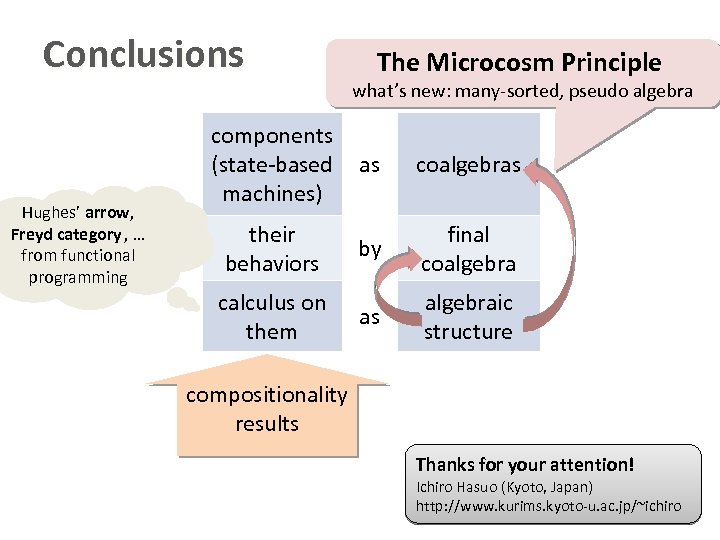
Conclusions Hughes’ arrow, Freyd category , … from functional programming components (state-based machines) their behaviors calculus on them The Microcosm Principle what’s new: many-sorted, pseudo algebra as coalgebras by final coalgebra as algebraic structure compositionality results Thanks for your attention! Ichiro Hasuo (Kyoto, Japan) http: //www. kurims. kyoto-u. ac. jp/~ichiro

Conclusion

Compositionality theorem Assume ¡ ¡ ¡ C is an L-category F : C C is a lax L-functor there is a final coalgebra Z FZ 1. Coalg F is an L-category obtaining