Co-NP problems on random inputs Paul Beame University

Co-NP problems on random inputs Paul Beame University of Washington

Basic idea z. NP is characterized by a simple property - having short certificates of membership z. Show that co-NP doesn’t have this property ywould separate P from NP so probably quite hard y. Lots of nice, useful baby steps towards answering this question 2

Certifying language membership z. Certificate of satisfiability y. Satisfying truth assignment y. Always short, SAT NP z. Certificate of unsatisfiability y? ? ? ytranscript of failed search for satisfying truth assignment y. Frege-Hilbert proofs, resolution y. Can they always be short? If so then NP=co-NP. 3

Proof systems z. A proof system for L is a polynomial time algorithm A s. t. for all inputs x yx is in L iff there exists a certificate P s. t. A accepts input (P, x) z. Complexity of a proof system y. How big |P| has to be in terms of |x| z NP = {L: L has polynomial-size proofs} 4

Propositional proof systems z. A propositional proof system is a polynomial time algorithm A s. t. for all formulas F y. F is unsatisfiable iff ythere exists a certificate P s. t. A accepts input (P, F) 5

Sample propositional proof systems z. Truth tables z. Axiom/Inference systems, e. g. ymodus ponens A, (A -> B) | B yexcluded middle | (A v ~A) z. Tableaux/Model Elimination systems ysearch through sub-formulas of input formula that might be true simultaneously ye. g. if ~(A -> B) is true A must be true and B must be false 6

Frege Systems z. Finite # of axioms/inference rules z. Proof of unsatisfiability of F - sequence F 1, …, Fr of formulas s. t. y. F 1 = F yeach Fj is an axiom or follows from previous ones via an inference rule y. Fr = L trivial falsehood z. All of equivalent complexity up to poly 7

Resolution z Frege-like system using CNF clauses only z Start with original input clauses of CNF F z Resolution rule y(A v x), (B v ~x) | (A v B) z Goal: derive empty clause L z Most-popular systems for practical theoremproving 8

Davis-Putnam (DLL) Procedure z. Both ya proof system ya collection of algorithms for finding proofs z. As a proof system y a special case of resolution where the pattern of inferences forms a tree. z. The most widely used family of complete algorithms for satisfiability 9

Simple Davis-Putnam Algorithm z Refute(F) y. While (F contains a clause of size 1) xset variable to make that clause true xsimplify all clauses using this assignment y. If F has no clauses then xoutput “F is satisfiable” and HALT y. If F does not contain an empty clause then x. Choose smallest-numbered unset variable x x. Run Refute( ) splitting rule x. Run Refute( ) 10

Hilbert’s Nullstellensatz z. System of polynomials Q 1(x 1, …, xn)=0, …, Qm(x 1, …, xn)=0 over field K has no solution in any extension field of K iff there exist polynomials P 1(x 1, …, xn), …, Pm(x 1, …, xn) in K[x 1, …, xn] s. t. 11

Nullstellensatz proof system z. Clause (x 1 v ~x 2 v x 3) becomes equation (1 -x 1)x 2(1 -x 3)=0 z. Add equations xi 2 -xi =0 for each variable z. Proof: polynomials P 1, …, Pm+n proving unsatisfiability 12

Polynomial Calculus z Similar to Nullstellensatz except: y. Begin with Q 1, …, Qm+n as before y. Given polynomials R and S can infer xa R + b S for any a, b in K xx i R y. Derive constant polynomial 1 y. Degree = maximum degree of polynomial appearing in the proof y. Can find proof of degree d in time n. O(d) using Groebner basis-like algorithm 13

Cutting Planes z Introduced to relate integer and linear programming: y. Clause (x 1 v ~x 2 v x 3) becomes inequality x 1+1 -x 2+x 3 1 y. Add xi 0 and 1 -xi 0 z. Derive 0 1 using rules for adding inequalities and Division Rule: zacx+bcy d implies ax+by d/c 14

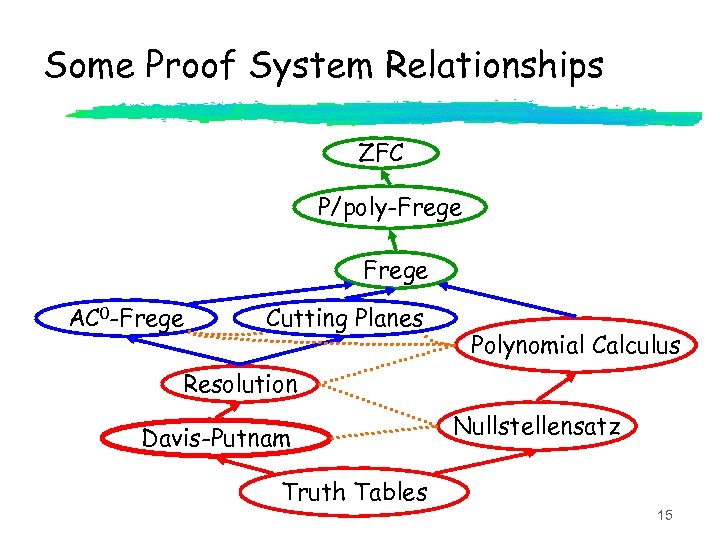
Some Proof System Relationships ZFC P/poly-Frege AC 0 -Frege Cutting Planes Polynomial Calculus Resolution Davis-Putnam Truth Tables Nullstellensatz 15

Random k-CNF formulas z. Make m independent choices of one of the clauses of length k z D = m/n is the clause-density of the formula z. Distribution 16

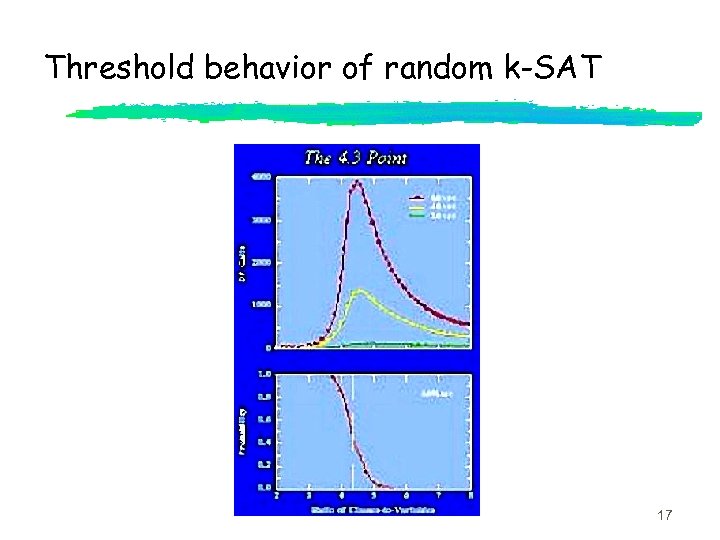
Threshold behavior of random k-SAT 17

Contrast with. . . z. Theorem [CS]: For every constant D, random k-CNF formulas almost certainly require resolution proofs of size 2 W(n) z. What is the dependence on D ? 18

Width of resolution proofs z. If P is a resolution proof width(P) = length of longest clause in P z. Theorem [BW]: Every Davis-Putnam (DLL) proof of size S can be converted to one of width log 2 S z. Theorem [BW]: Every resolution proof of size S can be converted to one of width 19

Sub-critical Expansion z F - a set of clauses zs(F) - minimum size subset of F that is unsatisfiable z d F - boundary of F - set of variables appearing in exactly one clause of F ze(F) - sub-critical expansion of F = max min { |d G|: G s s(F) F, s/2 < |G| s} 20

Width and expansion z. Lemma [CS] : If P is a resolution proof of F then width(P) e(F). s/2 to s s(F) G contains d G L 21

Consequences z. Corollaries: y. Any Davis-Putnam (DLL) proof of F requires size at least 2 e(F) y. Any resolution proof of F requires size at least 22

s(F) and e(F) for random formulas z. If F is a random formula from then ys(F) is W (n/D 1/(k-2)) almost certainly ye(F) is W (n/D 2/(k-2)+e) almost certainly z. Proved for Hypergraph expansion 23

Hypergraph Expansion z F - hypergraph z d F - boundary of F - set of degree 1 vertices of F zs. H(F) - minimum size subset of F that does not have a System of Distinct Representatives ze. H(F) - sub-critical expansion of F max min { |d G|: G s s. H(F) F, s/2 < |G| s} 24

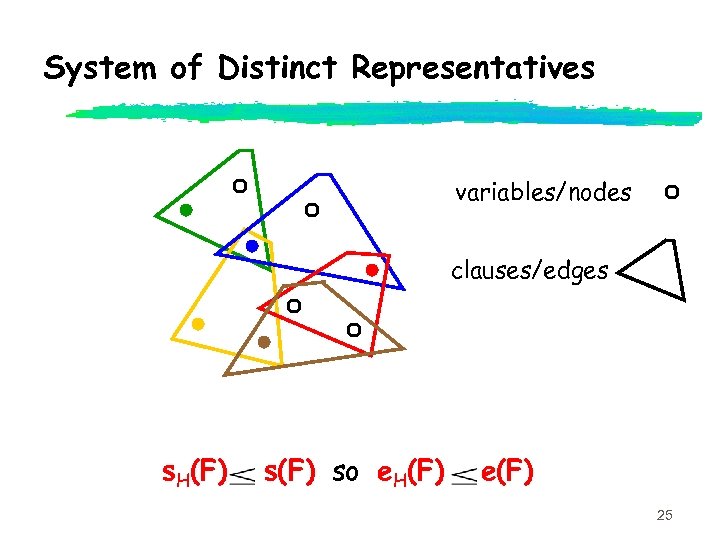
System of Distinct Representatives variables/nodes clauses/edges s. H(F) so e. H(F) e(F) 25

Density and SDR’s z The density of a hypergraph is #(edges)/#(vertices) z Hall’s Theorem: A hypergraph F has a system of distinct representatives iff every subgraph has density at most 1. 26

Density and Boundary z. A k-uniform hypergraph of density bounded below 2/k, say 2/k-e , has average degree bounded below 2 y constant fraction of nodes are in the boundary 27

Density of random formulas z. Fix set S of vertices/variables of size r y. Probability p that a single edge/clause lands in S is at most (r/n)k y. Probability that S contains at least q edges is at most 28

s(F) for random formulas z. Apply for q=r+1 for all r up to s using union bound: zfor s = O(n/D 1/(k-2)) 29

e(F) for random formulas z. Apply for q=2 r/k for all r between s/2 and s using union bound: zfor s = Q(n/D 2/(k-2)) 30

Hypergraph Expansion and Polynomial Calculus z. Theorem [BI]: The degree of any polynomial calculus or Nullstellensatz proof of unsatisfiability of F is at least e. H(F)/2 if the characteristic is not 2. z Groebner basis algorithm bound is only n. O(e. H(F)) 31

k-CNF and parity equations z Clause (x 1 v ~x 2 v x 3) is implied by x 1+(x 2+1)+x 3 = 1 (mod 2) i. e. x 1+x 2+x 3 = 0 (mod 2) z Derive contradiction 0 = 1 (mod 2) by adding collections of equations z # of variables in longest line is at least e. H(F) 32

Parity equations and polynomial calculus z Given equations of form yx 1+x 2+x 3 = 0 (mod 2) z Polynomial equation yi 2 -1=0 for each variable yyi = 2 xi-1 z Polynomial equation y 1 y 2 y 3 -1=0 ywould be y 1 y 2 y 3+1=0 if RHS were 1 z Imply the old Nullstellensatz equations if char(K) is not 2 33

Lower bounds z. For random k-CNF chosen from almost certainly for any e>0: y. Any Davis-Putnam proof requires size y. Any resolution proof requires size y. Any polynomial calculus proof requires degree 34

Upper Bound z Theorem [BKPS]: For F chosen from and D above threshold, the simple Davis. Putnam (DLL) algorithm almost certainly finds a refutation of size z and this is a tight bound. . . 35

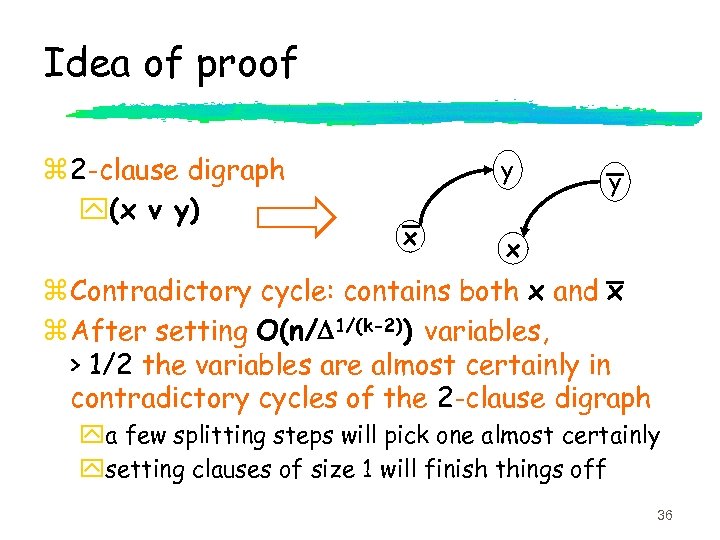
Idea of proof z 2 -clause digraph y(x v y) y x z Contradictory cycle: contains both x and x z After setting O(n/D 1/(k-2)) variables, > 1/2 the variables are almost certainly in contradictory cycles of the 2 -clause digraph ya few splitting steps will pick one almost certainly ysetting clauses of size 1 will finish things off 36

Implications z Random k-CNF formulas are provably hard for the most common proof search procedures. z. This hardness extends well beyond the phase transition. y. Even at clause ratio D=n 1/3, current algorithms on random 3 -CNF formulas have asymptotically the same running time as the best factoring algorithms. 37

Random graph k-colourability z. Random graph G(n, p) where each edge occurs independently with probability p y. Sharp threshold for whether or not graph is k-colourable, e. g. p ~ 4. 6/n for k=3 z. What about proofs that the graph is not k-colourable? 38

Lower Bound z Theorem [BCM 99]: Non-k-colourability requires exponentially large resolution proofs z Basic proof idea: ysame outline as before ynotion of boundary of a sub-graph xset of vertices of degree < k ys(G) smallest non-k-colourable sub-graph 39

Challenges z. Better bound for e(F) for random F y. Can it be Q(s(F)) ? x. If so, the simple Davis-Putnam algorithm has asymptotically best possible exponent of any DP algorithm. z. Extend lower bounds to other proof systems ymust be based on something other than expansion since certain formulas with high expansion have small Cutting Planes proofs. 40

Challenges z. Conjecture: Random k-CNF formulas are hard for Frege proofs z. Extend to other random co-NP problems y. Independent Set? x. Best algorithms only get within factor of 2 of the largest independent set in a random graph 41

Sources z [Cook, Reckhow 79] z [Chvatal, Szemeredi 89] z [Mitchell, Selman, Levesque 93] z [Beame, Pitassi 97] z [Beame, Karp, Pitassi, Saks 98] z [Beame, Pitassi 98] z [Ben-Sasson, Wigderson 99] z [Ben-Sasson, Impagliazzo 99] z [Beame, Culberson, Mitchell 99] 42

Circuit Complexity z P/poly - polysize circuits z NC 1 - polysize formulas z CNF - polysize CNF formulas z AC 0 - constant-depth polysize circuits using and/or/not z AC 0[m] - also = 0 mod m tests z TC 0 - threshold instead 43

C-Frege Proofs z Given circuit complexity class C can define C-Frege proofs to be Frege-like proofs that manipulate circuits in C rather than formulas z Frege = NC 1 -Frege z Resolution = CNF-Frege z Extended-Frege = P/poly-Frege z AC 0[m]-Frege z TC 0 -Frege 44