co NP Having Proofs for Incorrectness Complexity 1

co. NP Having Proofs for Incorrectness Complexity 1

Introduction • Objectives: – To introduce the complexity class co. NP – To explore the primality problem. • Overview: – co. NP: Definition and examples – co. NP=NP? and NP=P? – PRIMES and Pratt’s theorem Complexity 2

Co. NP Def: Co. NP is the class of problems that have succinct non-membership witnesses. Complexity 3

VALIDITY • Instance: A Boolean formula • Problem: To decide if the formula is valid (i. e satisfiable by all possible assignments) A valid Boolean formula: An invalid Boolean formula: Complexity 4

VALIDITY is in co. NP • Guess an assignment • Verify it doesn’t satisfy the formula )x)=F Complexity x Indeed it doesn’t satisfy x! 5

Using what we Know about NP • By definition, the complement of every NP language is in co. NP. • The complement of a co. NP language is NP. VALIDITY is in co. NP! Complexity Since SAT is in NP. . . 6

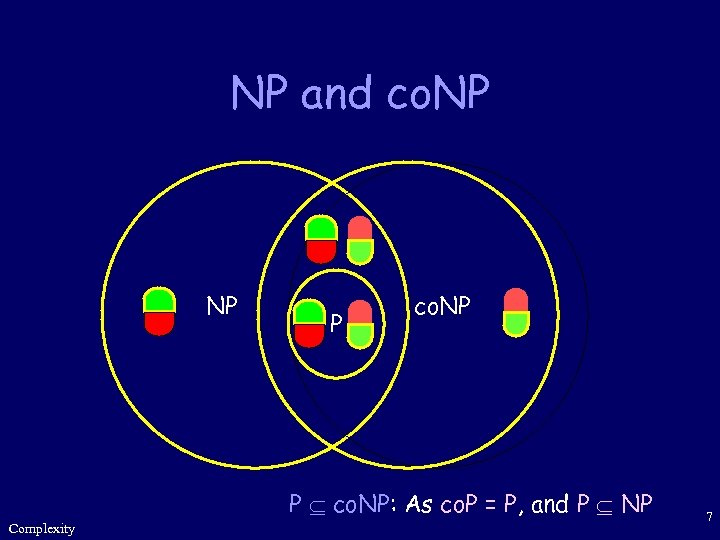NP and co. NP NP P co. NP P co. NP: As co. P = P, and P NP Complexity 7

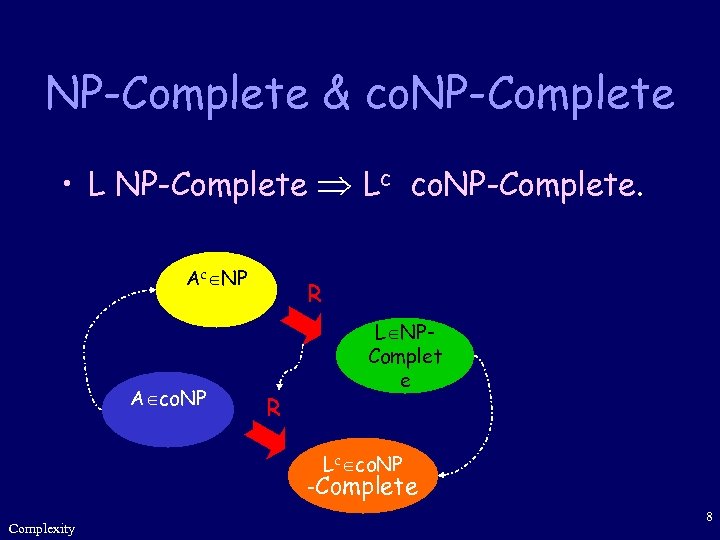NP-Complete & co. NP-Complete • L NP-Complete Lc co. NP-Complete. Ac NP A co. NP R R L NPComplet e Lc co. NP -Complete Complexity 8

NP=P? & co. NP=NP? Claim: P=NP implies co. NP=NP. Proof: P=co. P, hence if P=NP, NP=co. NP. Does the opposite direction also hold? Complexity 9

co. NP=NP? & Completeness in co. NP Claim: If a co. NP-Complete problem L is in NP, under Karp reduction, then co. NP=NP. Proof: in that case, any A co. NP, must be in NP A co. NP A NP R L co. NPL NP Complete Complexity 10

What’s co. NP’s Proper Position? NP Complexity P 11

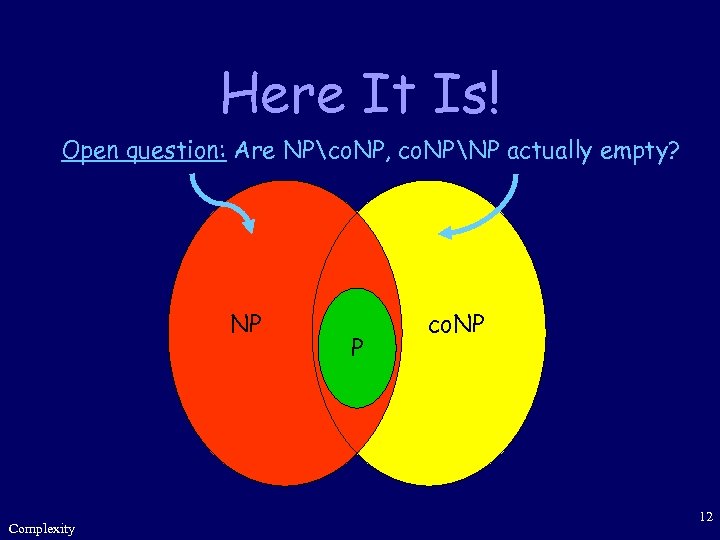Here It Is! Open question: Are NPco. NP, co. NPNP actually empty? NP Complexity P co. NP 12

PRIMES • Instance: A number in binary representation. • Problem: To decide if this number is prime. Yes instance: No instance: Complexity 10111 10110 13

Is Primes in P ? ! What’s the problem with the following algorithm? Input: a number N Output: is N prime? for i in 2. . N do for j in 2. . N do if i*j=N, return FALSE return TRUE Complexity 14

PRIMES is in co. NP Don’t forget to make sure this takes polynomial time • Given a number N • Guess two numbers i and j • Verify i*j=N. . . # 1 0 1 1 0 # . . . # 1 0 1 1 # 1 0 #. . . Complexity 15

PAP 222 -227 Is PRIMES in NP? Claim: A number p > 2 is prime iff a number 1

Pratt’s Theorem: PRIMES is in NP co. NP. Proof: Assuming the above claim we need to find some type of a guess that can be easily verify. . . Complexity 17

What Can We Get By Guessing r? We first need to verify rp-1=1 (mod p) BUT rp-1 mod p requires only poly-space Complexity rp-1 can be superexponential! 18

What Can We Get By Guessing r? We first need to verify rp-1=1 (mod p) Performing p-1 multiplications is not polynomial! Complexity But you can start with r and square log(p-1) times! 19

Verifying the Second Requirement Next we need to verify, that prime divisor q of p-1: r(p-1)/q 1 (mod p) Lemma: Any n>1 has k logn prime divisors. Proof: Denote the prime divisors of n by q 1, . . . , qk. Note that n q 1·. . . ·qk and all qi 2. Thus n 2 k, i. e - k logn. Complexity 20

Verifying the Second Requirement Next we need to verify, that prime divisor q of p-1: r(p-1)/q 1 (mod p) Obviously I wouldn’t! I’d just guess them! Complexity How would you find the prime divisors of p-1? 21

Verifying the Second Requirement Next we need to verify, that prime divisor q of p-1: r(p-1)/q 1 (mod p) Exactly the same way! Complexity How would you verify they are prime? 22

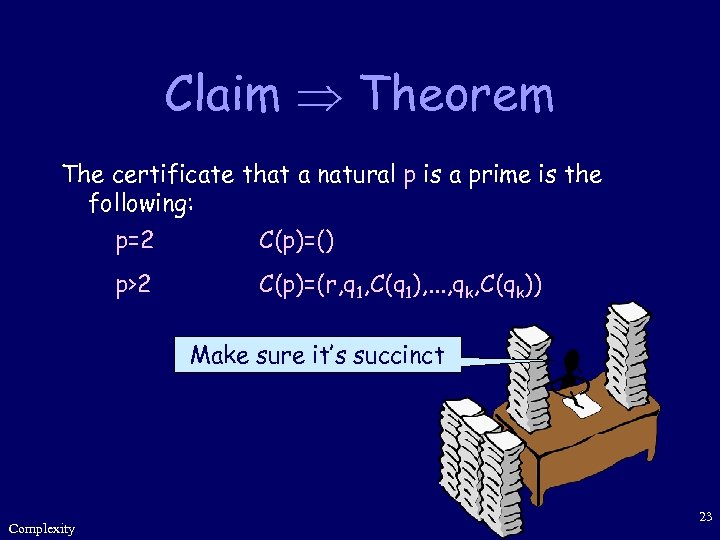Claim Theorem The certificate that a natural p is a prime is the following: p=2 C(p)=() p>2 C(p)=(r, q 1, C(q 1), . . . , qk, C(qk)) Make sure it’s succinct Complexity 23

The Verification 1. If p=2, accept 2. Otherwise, verify rp-1=1 (mod p). 3. Check that p can be reduced to 1 by repeated divisions by the qi’s. 4. Check r(p-1)/qi 1 (mod p) for all the qi’s. 5. Recursively apply this algorithm upon every qi, C(qi) Make sure it takes poly-time Complexity 24

Proof of Claim • Need to show that every prime satisfies both conditions and • that any number satisfying both conditions is a prime Complexity 25

Euler’s Function • (n) = { m | 1 m < n AND gcd(m, n)=1 } • Euler’s function: (n)=| (n)| Example: (12)={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} (12)=4 Observe: For any prime p, (p)={1, . . . , p-1} Complexity 26

Fermat’s Little Theorem: Let p be a prime number 0 < a < p, ap-1 =1 (mod p) Example: p=5; a=2 25 -1 mod 5 = 16 mod 5 = 1 Complexity 27

Observation 0

Fermat’s Theorem: Proof Therefore, for any 0

Generalization Claim: For all a (n) , a (n)=1 (mod n). Example: n=8, (8) = {1, 3, 5, 7} 34=1 (mod 8) Complexity 30

Generalization: Proof Again: For any a (n), a· (n)= (n( Again: m (n)m 0 (mod n) Example: (8) * (mod 3 5 7 And 8) 1 claim follows. the 1 3 5 7 3 3 1 7 5 5 5 7 1 3 7 Complexity 1 7 5 3 1 31

What have we got So Far • We know if p is prime condition (1) holds for all a • For non prime n, condition (1) may hold for some a but then a (n)=1 (mod n) as well, hence an-1 - (n)=1 (mod n) Complexity 32

Exponents Def: If m (p), the exponent of m is the smallest integer k > 0 such that mk=1 (mod p). Example: p=7, m=4 (7), the exponent of 4 is 3. Complexity 33

All Residues Have Exponents • • Complexity Let s (p). j > i N that satisfy si=sj (mod p). si is indivisible by p. sj-i=1 (mod p). 34

Regarding Exponents • Observation: The only powers of m that are 1 (mod p) are multiplies of its exponent! • Assuming rp-1 = 1 (mode p), by Fermat’s theorem, r’s exponent divides p-1 Complexity 35

Non Primes Must Fail • • • For a non prime n: It must be that (p) < p-1. Assume there is r s. t rp-1=1 (mod p) We’ve shown r (p)=1 (mod p) So there is also a prime divisor q of p 1, s. t r(p-1)/q =1 mod p. • We may conclude: if both conditions hold p is prime! Complexity 36

An Equivalent Definition of Euler’s Function Using Prime Divisors • Let p be a prime divisor of n. • The probability p divides a candidate is 1/p. • Thus: . . . all the residues modulo n are candidates for (n) Complexity 37

Corollaries Corollary: If gcd(m, n)=1, (mn)= (m) (n). Proof: (6)=|{1, 5}|=2 (2)=|{1}|=1 (3)=|{1, 2}|=2 Complexity 38

The Chinese Remainder Theorem: If n is the product of distinct primes p 1, . . . , pk, for each k-tuple of residues (r 1, . . . , rk), where ri (pi), there is a unique r (n), where ri=r mod pi for every 1 i k. 21=7· 3 (21)={1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20} (3) ={1, 2} (7) ={1, 2, 3, 4, 5, 6} Complexity 39

The Chinese Remainder Theorem Proof: If n is the product of distinct primes p 1, . . . , pk, then (n)= 1 i k(pi-1). This means | (n)|=| (p 1). . . (pk)|. The following is a 1 -1 correspondence between the two sets: r Complexity (r mod p 1, . . . , r mod pk) 40

Another Property of the Euler Function Claim: m|n (m)=n. Example: m|12 (m)= (1) + (2) + (3) + (4) + (6) + (12)= |{1}| + |{1, 2}| + |{1, 3}| + |{1, 5, 7, 11}|= 1 + 2 + 2 + 4 = 12 Complexity 41

Another Property of the Euler Function Claim: m|n (m)=n. Proof: Let 1 i lpiki be the prime factorization of n. (n)=n (1 -1/p) p|n m|n (m)= Since (ab)= (a) (b) Complexity telescopic sum 42

Group together Residues with Same Exponent • Fix a p and let R(k) denote the number of residues with exponent k. • If k does not divide p-1, R(k)=0. • Can you upper bound R(k)? Complexity 43

Polynomials Have Few Roots Claim: Any polynomial of degree k that is not identically zero has at most k distinct roots modulo p. Proof: By induction on k. Trivially holds for k=0. Suppose it also holds for some k-1. By way of contradiction, assume x 1, . . . , xk+1 are roots of (x)=akxk+. . . +a 0. ’(x)= (x)-ak 1 i k(x-xi) is of degree k-1 and not identically zero. x 1, . . . , xk are its roots Contradiction! Complexity 44

How Many Residues Can Share an Exponent? • Conclusion: There at most k residues of exponent k. • Claim: R(k) ≤ (k) • Proof: – Let s be a residue of exponent k. – (1, s, s 2, …, sk-1) are k distinct solutions of xk=1 (mod p) (why? ) – If sl has exponent k, l (k) (otherwise its exponent is lower). Complexity 45

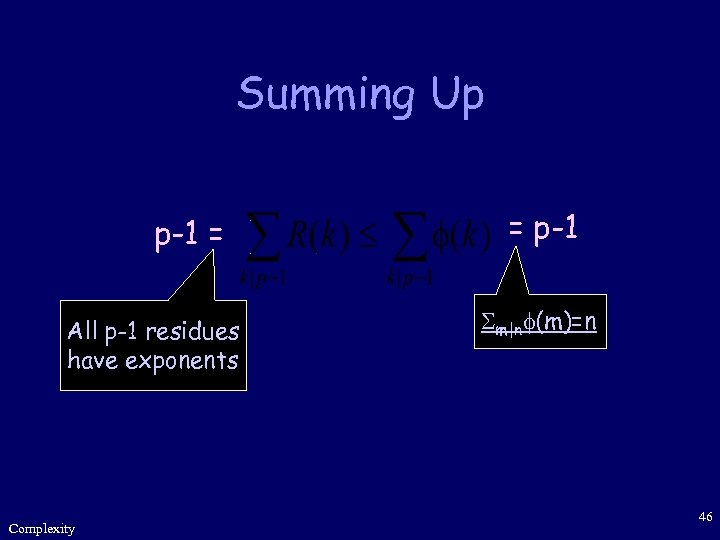Summing Up p-1 = All p-1 residues have exponents Complexity = p-1 m|n (m)=n 46

Summing Up R(k)= (k) for all divisors of p-1 R(p-1) = (p-1) > 0 p has at least one primitive root Complexity 47

Where Do We Stand? • We’ve shown every prime has a primitive root. Hence any prime satisfied both conditions • We’ve previously shown any non prime does not satisfy both conditions Complexity 48

Q. E. D! • This finally proves the validity of our alternative characterization of primes, • which implies that PRIMES is in NP. Complexity 49

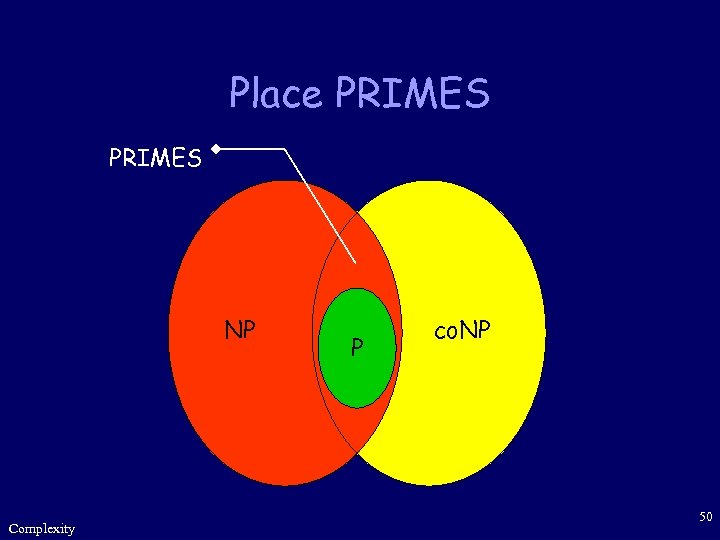Place PRIMES NP Complexity P co. NP 50

Summary • We’ve studied the complexity class co. NP, • and explored the relations between co. NP and other classes, such as P and NP. • We’ve introduced PRIMES and showed it’s in NP co. NP, though it’s believed not to be in P. Complexity 51