CMU SCS Sensor data mining and forecasting Christos

Скачать презентацию CMU SCS Sensor data mining and forecasting Christos

f3c96ab92cbe0c32dd6e9dc096ef34d9.ppt

Количество слайдов: 112

CMU SCS Sensor data mining and forecasting Christos Faloutsos CMU christos@cs. cmu. edu Telcordia 2003 C. Faloutsos

CMU SCS Outline • • • Problem definition - motivation Linear forecasting - AR and AWSOM Coevolving series - MUSCLES Fractal forecasting - F 4 Other projects – graph modeling, outliers etc Telcordia 2003 C. Faloutsos 2

CMU SCS Problem definition • Given: one or more sequences x 1 , x 2 , … , xt , … (y 1, y 2, … , yt, … …) • Find – forecasts; patterns – clusters; outliers Telcordia 2003 C. Faloutsos 3

CMU SCS Motivation - Applications • Financial, sales, economic series • Medical – ECGs +; blood pressure etc monitoring – reactions to new drugs – elderly care Telcordia 2003 C. Faloutsos 4

CMU SCS Motivation - Applications (cont’d) • ‘Smart house’ – sensors monitor temperature, humidity, air quality • video surveillance Telcordia 2003 C. Faloutsos 5

CMU SCS Motivation - Applications (cont’d) • civil/automobile infrastructure – bridge vibrations [Oppenheim+02] – road conditions / traffic monitoring Telcordia 2003 C. Faloutsos 6

CMU SCS Stream Data: automobile traffic # cars Automobile traffic 2000 1800 1600 1400 1200 1000 800 600 400 200 0 Telcordia 2003 time C. Faloutsos 7

CMU SCS Motivation - Applications (cont’d) • Weather, environment/anti-pollution – volcano monitoring – air/water pollutant monitoring Telcordia 2003 C. Faloutsos 8

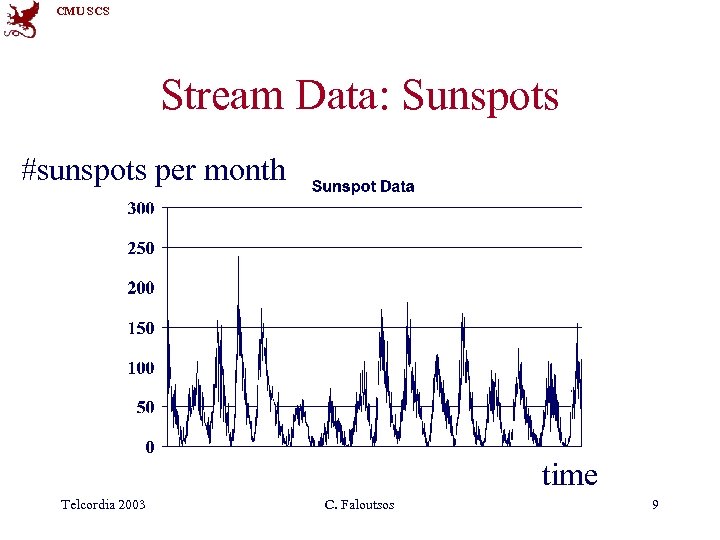CMU SCS Stream Data: Sunspots #sunspots per month time Telcordia 2003 C. Faloutsos 9

CMU SCS Motivation - Applications (cont’d) • Computer systems – ‘Active Disks’ (buffering, prefetching) – web servers (ditto) – network traffic monitoring –. . . Telcordia 2003 C. Faloutsos 10

CMU SCS Stream Data: Disk accesses #bytes Telcordia 2003 C. Faloutsos time 11

CMU SCS Settings & Applications • One or more sensors, collecting time-series data Telcordia 2003 C. Faloutsos 12

CMU SCS Settings & Applications Each sensor collects data (x 1, x 2, …, xt, …) Telcordia 2003 C. Faloutsos 13

CMU SCS Settings & Applications Sensors ‘report’ to a central site Telcordia 2003 C. Faloutsos 14

CMU SCS Settings & Applications Problem #1: Finding patterns in a single time sequence Telcordia 2003 C. Faloutsos 15

CMU SCS Settings & Applications Problem #2: Finding patterns in many time sequences Telcordia 2003 C. Faloutsos 16

CMU SCS Problem #1: Goal: given a signal (eg. , #packets over time) Find: patterns, periodicities, and/or compress count lynx caught per year (packets per day; temperature per day) year Telcordia 2003 C. Faloutsos 17

CMU SCS Problem#1’: Forecast Number of packets sent Given xt, xt-1, …, forecast xt+1 90 80 70 60 50 40 30 20 10 0 ? ? 1 3 5 7 9 11 Time Tick Telcordia 2003 C. Faloutsos 18

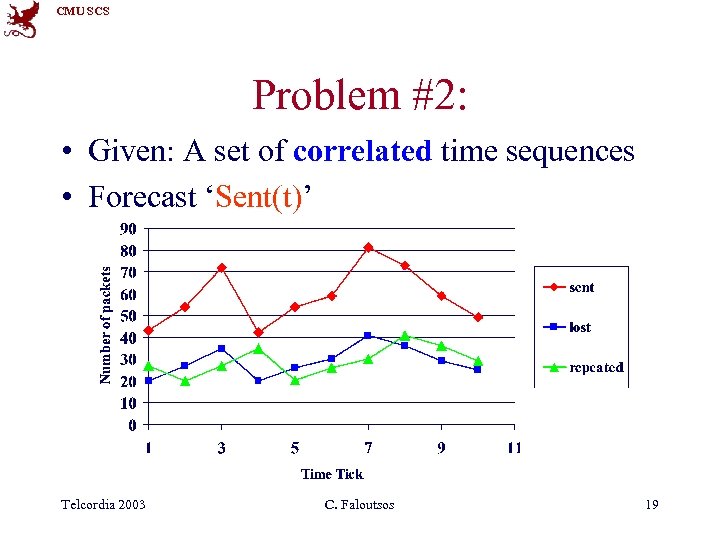CMU SCS Problem #2: • Given: A set of correlated time sequences • Forecast ‘Sent(t)’ Telcordia 2003 C. Faloutsos 19

CMU SCS Differences from DSP/Stat • Semi-infinite streams – we need on-line, ‘any-time’ algorithms • Can not afford human intervention – need automatic methods • sensors have limited memory / processing / transmitting power – need for (lossy) compression Telcordia 2003 C. Faloutsos 20

CMU SCS Important observations Patterns, rules, compression and forecasting are closely related: • To do forecasting, we need – to find patterns/rules • good rules help us compress • to find outliers, we need to have forecasts – (outlier = too far away from our forecast) Telcordia 2003 C. Faloutsos 21

CMU SCS Pictorial outline of the talk Telcordia 2003 C. Faloutsos 22

CMU SCS Outline • Problem definition - motivation • Linear forecasting – AR – AWSOM • Coevolving series - MUSCLES • Fractal forecasting - F 4 • Other projects – graph modeling, outliers etc Telcordia 2003 C. Faloutsos 23

CMU SCS Mini intro to A. R. Telcordia 2003 C. Faloutsos 24

CMU SCS Forecasting "Prediction is very difficult, especially about the future. " - Nils Bohr http: //www. hfac. uh. edu/Media. Futures/ thoughts. html Telcordia 2003 C. Faloutsos 25

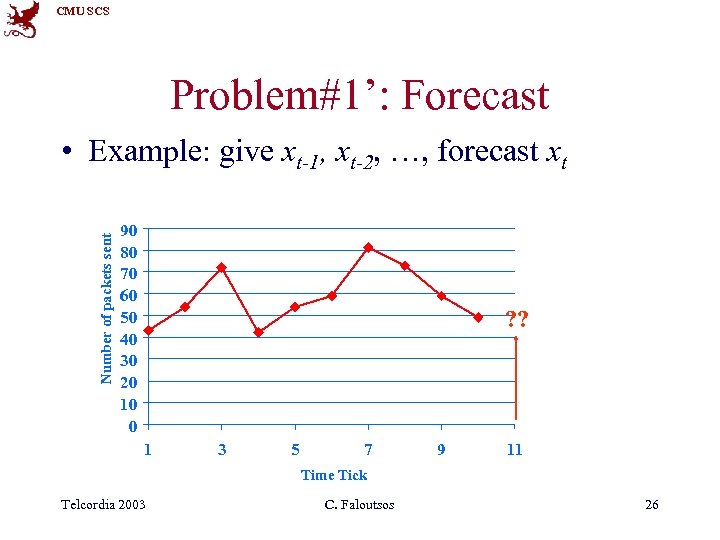CMU SCS Problem#1’: Forecast Number of packets sent • Example: give xt-1, xt-2, …, forecast xt 90 80 70 60 50 40 30 20 10 0 ? ? 1 3 5 7 9 11 Time Tick Telcordia 2003 C. Faloutsos 26

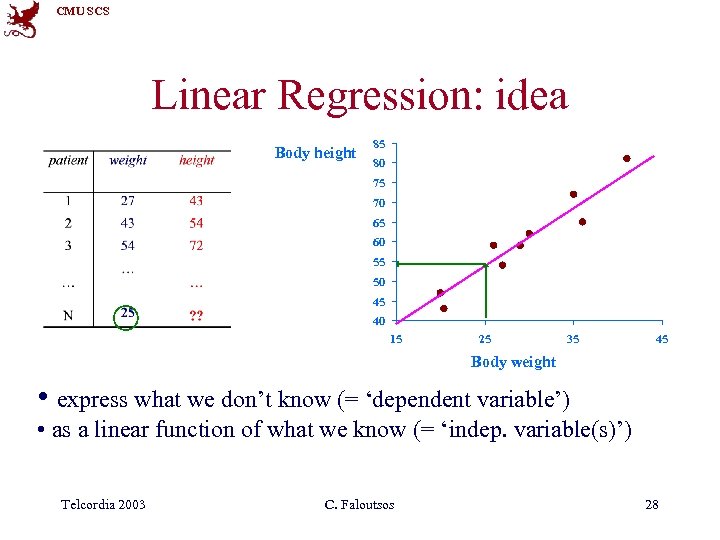CMU SCS Linear Regression: idea Body height 85 80 75 70 65 60 55 50 45 40 15 25 35 45 Body weight • express what we don’t know (= ‘dependent variable’) • as a linear function of what we know (= ‘indep. variable(s)’) Telcordia 2003 C. Faloutsos 28

CMU SCS Linear Auto Regression: Telcordia 2003 C. Faloutsos 29

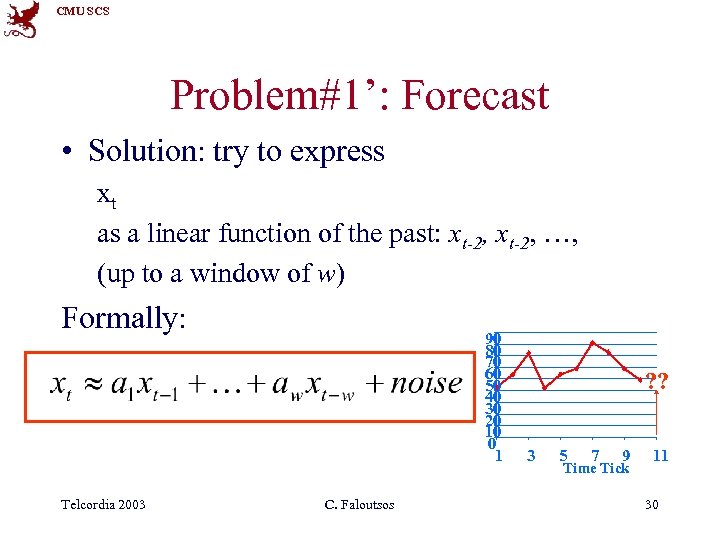CMU SCS Problem#1’: Forecast • Solution: try to express xt as a linear function of the past: xt-2, …, (up to a window of w) Formally: Telcordia 2003 90 80 70 60 50 40 30 20 10 0 1 C. Faloutsos ? ? 3 5 7 9 Time Tick 11 30

CMU SCS Number of packets sent (t) Linear Auto Regression: 85 ‘lag-plot’ 80 75 70 65 60 55 50 45 40 15 25 35 45 Number of packets sent (t-1) • lag w=1 • Dependent variable = # of packets sent (S [t]) • Independent variable = # of packets sent (S[t-1]) Telcordia 2003 C. Faloutsos 31

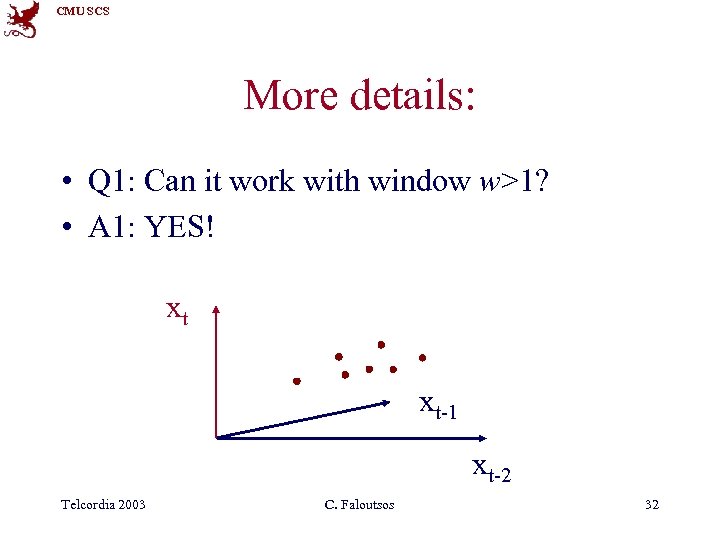CMU SCS More details: • Q 1: Can it work with window w>1? • A 1: YES! xt xt-1 xt-2 Telcordia 2003 C. Faloutsos 32

CMU SCS More details: • Q 1: Can it work with window w>1? • A 1: YES! (we’ll fit a hyper-plane, then!) xt xt-1 xt-2 Telcordia 2003 C. Faloutsos 33

CMU SCS More details: • Q 1: Can it work with window w>1? • A 1: YES! (we’ll fit a hyper-plane, then!) xt xt-1 xt-2 Telcordia 2003 C. Faloutsos 34

CMU SCS Even more details • Q 2: Can we estimate a incrementally? • A 2: Yes, with the brilliant, classic method of ‘Recursive Least Squares’ (RLS) (see, e. g. , [Chen+94], or [Yi+00], for details) • Q 3: can we ‘down-weight’ older samples? • A 3: yes (RLS does that easily!) Telcordia 2003 C. Faloutsos 35

CMU SCS Mini intro to A. R. Telcordia 2003 C. Faloutsos 36

CMU SCS How to choose ‘w’? • goal: capture arbitrary periodicities • with NO human intervention • on a semi-infinite stream Telcordia 2003 C. Faloutsos 37

CMU SCS Problem: • in a train of spikes (128 ticks apart) • any AR with window w < 128 will fail What to do, then? Telcordia 2003 C. Faloutsos 39

CMU SCS Answer (intuition) • Do a Wavelet transform (~ short window DFT) • look for patterns in every frequency Telcordia 2003 C. Faloutsos 40

CMU SCS Intuition • Why NOT use the short window Fourier transform (SWFT)? • A: how short should be the window? freq Telcordia 2003 w’ time C. Faloutsos 41

CMU SCS wavelets • main idea: variable-length window! f t Telcordia 2003 C. Faloutsos 42

CMU SCS Advantages of Wavelets • Better compression (better RMSE with same number of coefficients - used in JPEG-2000) • fast to compute (usually: O(n)!) • very good for ‘spikes’ • mammalian eye and ear: Gabor wavelets Telcordia 2003 C. Faloutsos 43

CMU SCS Wavelets - intuition: • Q: baritone/silence/ soprano - DWT? f t value time Telcordia 2003 C. Faloutsos 44

CMU SCS Wavelets - intuition: • Q: baritone/soprano - DWT? f t value time Telcordia 2003 C. Faloutsos 45

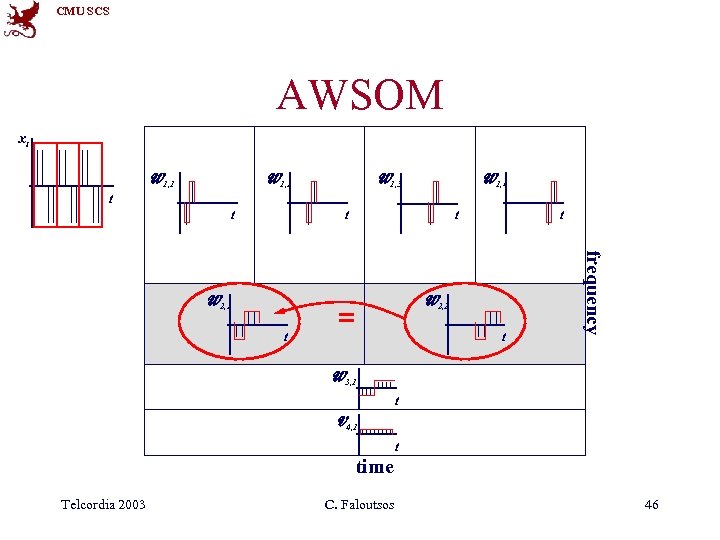CMU SCS AWSOM xt W 1, 1 W 1, 3 W 1, 2 W 1, 4 t t t W 2, 2 = t frequency W 2, 1 t W 3, 1 t V 4, 1 t time Telcordia 2003 C. Faloutsos 46

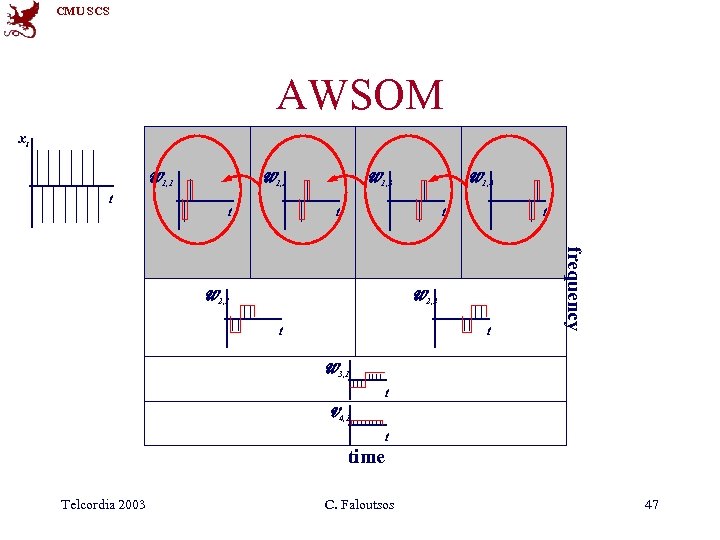CMU SCS AWSOM xt W 1, 2 W 1, 1 t t W 1, 3 W 1, 4 t t W 2, 2 t t frequency W 2, 1 t W 3, 1 t V 4, 1 t time Telcordia 2003 C. Faloutsos 47

CMU SCS AWSOM - idea Wl, t-2 Wl, t-1 Wl, t Wl’, t’-2 Telcordia 2003 Wl’, t’-1 Wl’, t’ Wl, t Wl’, t’ C. Faloutsos l, 1 Wl, t-1 l, 2 Wl, t-2 … l’, 1 Wl’, t’-1 l’, 2 Wl’, t’-2 … 48

CMU SCS More details… • Update of wavelet coefficients (incremental) • Update of linear models (incremental; RLS) • Feature selection (single-pass) – Not all correlations are significant – Throw away the insignificant ones (“noise”) Telcordia 2003 C. Faloutsos 52

CMU SCS Results - Synthetic data AWSOM Telcordia 2003 AR Seasonal AR C. Faloutsos • Triangle pulse • Mix (sine + square) • AR captures wrong trend (or none) • Seasonal AR estimation fails 53

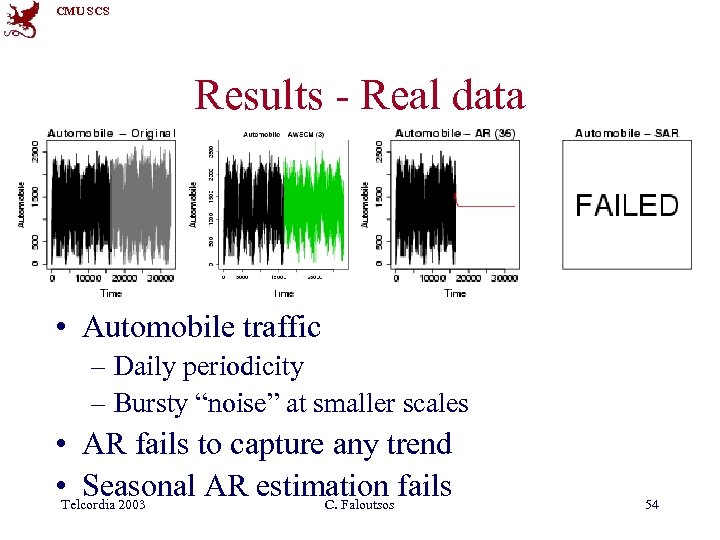CMU SCS Results - Real data • Automobile traffic – Daily periodicity – Bursty “noise” at smaller scales • AR fails to capture any trend • Telcordia 2003 Seasonal AR estimation fails C. Faloutsos 54

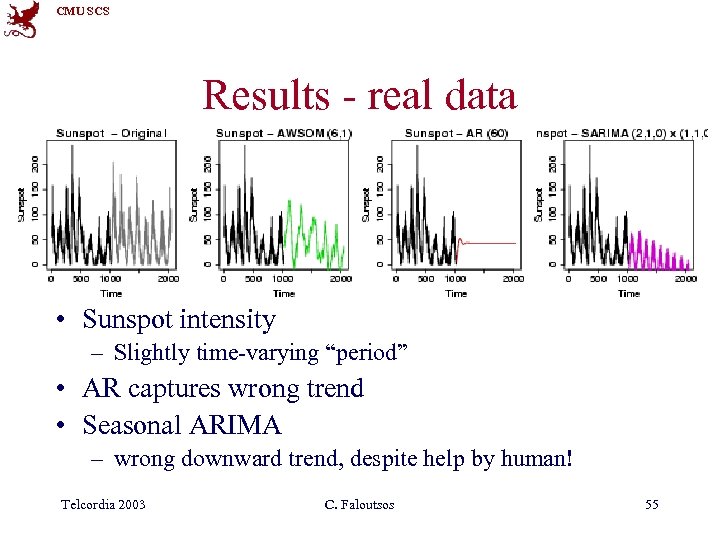CMU SCS Results - real data • Sunspot intensity – Slightly time-varying “period” • AR captures wrong trend • Seasonal ARIMA – wrong downward trend, despite help by human! Telcordia 2003 C. Faloutsos 55

CMU SCS Complexity • Model update Space: O lg. N + mk 2 O lg. N Time: O k 2 O 1 • Where – N: number of points (so far) – k: number of regression coefficients; fixed – m: number of linear models; O lg. N Telcordia 2003 C. Faloutsos 56

CMU SCS Conclusions • AWSOM: Automatic, ‘hands-off’ traffic modeling (first of its kind!) Telcordia 2003 C. Faloutsos 57

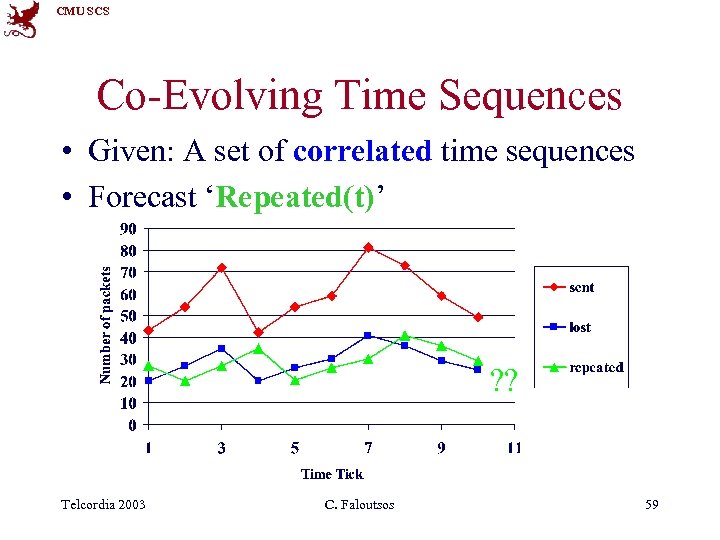CMU SCS Co-Evolving Time Sequences • Given: A set of correlated time sequences • Forecast ‘Repeated(t)’ ? ? Telcordia 2003 C. Faloutsos 59

CMU SCS Solution: Q: what should we do? Telcordia 2003 C. Faloutsos 60

CMU SCS Solution: Least Squares, with • Dep. Variable: Repeated(t) • Indep. Variables: Sent(t-1) … Sent(t-w); Lost(t-1) …Lost(t-w); Repeated(t-1), . . . • (named: ‘MUSCLES’ [Yi+00]) Telcordia 2003 C. Faloutsos 61

CMU SCS Examples - Experiments • Datasets – Modem pool traffic (14 modems, 1500 timeticks; #packets per time unit) – AT&T World. Net internet usage (several data streams; 980 time-ticks) • Measures of success – Accuracy : Root Mean Square Error (RMSE) Telcordia 2003 C. Faloutsos 62

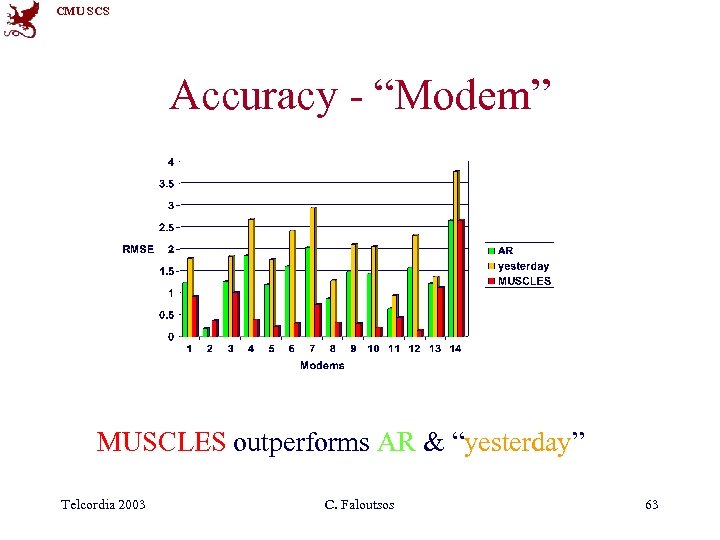CMU SCS Accuracy - “Modem” MUSCLES outperforms AR & “yesterday” Telcordia 2003 C. Faloutsos 63

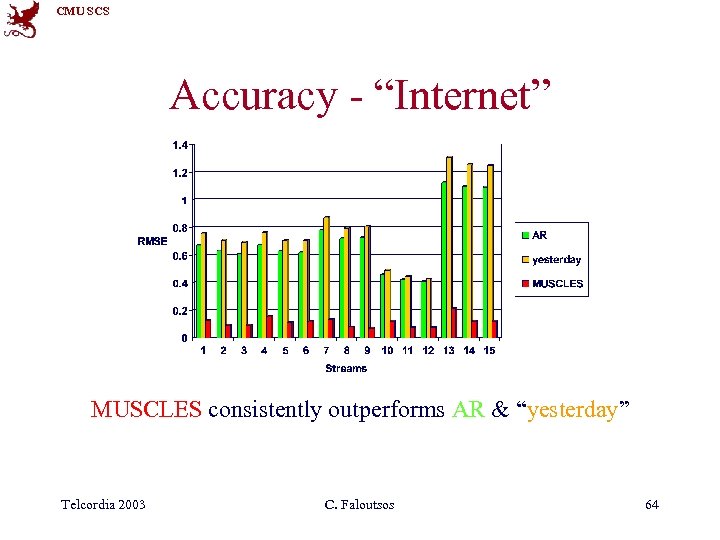CMU SCS Accuracy - “Internet” MUSCLES consistently outperforms AR & “yesterday” Telcordia 2003 C. Faloutsos 64

CMU SCS Detailed Outline • Non-linear forecasting – Problem – Idea – How-to – Experiments – Conclusions Telcordia 2003 C. Faloutsos 66

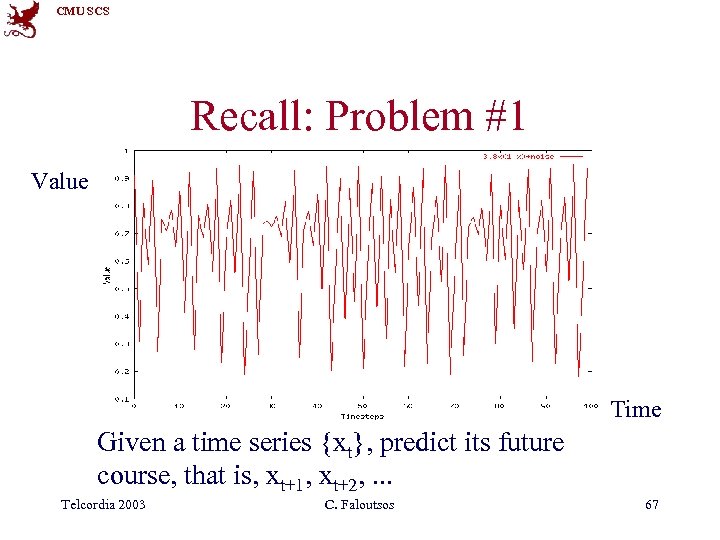CMU SCS Recall: Problem #1 Value Time Given a time series {xt}, predict its future course, that is, xt+1, xt+2, . . . Telcordia 2003 C. Faloutsos 67

CMU SCS How to forecast? • ARIMA - but: linearity assumption • ANSWER: ‘Delayed Coordinate Embedding’ = Lag Plots [Sauer 92] Telcordia 2003 C. Faloutsos 68

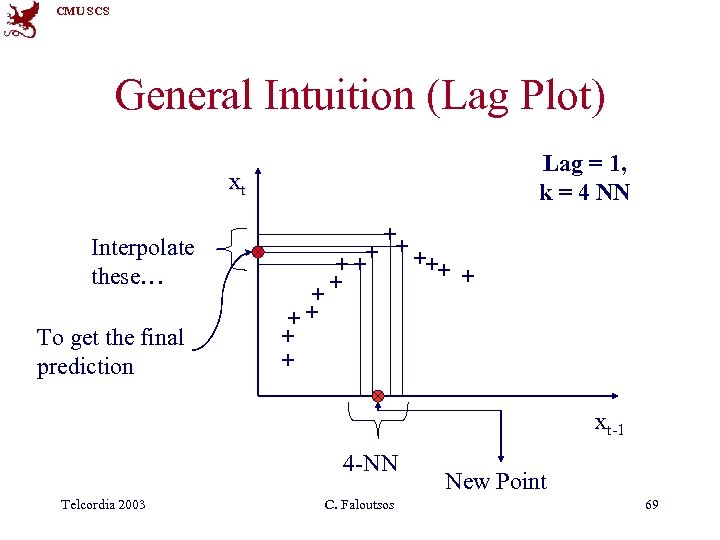CMU SCS General Intuition (Lag Plot) Lag = 1, k = 4 NN xt Interpolate these… To get the final prediction xt-1 4 -NN Telcordia 2003 C. Faloutsos New Point 69

CMU SCS Questions: • • Q 1: How to choose lag L? Q 2: How to choose k (the # of NN)? Q 3: How to interpolate? Q 4: why should this work at all? Telcordia 2003 C. Faloutsos 70

CMU SCS Q 1: Choosing lag L • Manually (16, in award winning system by [Sauer 94]) • Our proposal: choose L such that the ‘intrinsic dimension’ in the lag plot stabilizes [Chakrabarti+02] Telcordia 2003 C. Faloutsos 71

CMU SCS Fractal Dimensions • FD = intrinsic dimensionality Embedding dimensionality = 3 Intrinsic dimensionality = 1 Telcordia 2003 C. Faloutsos 72

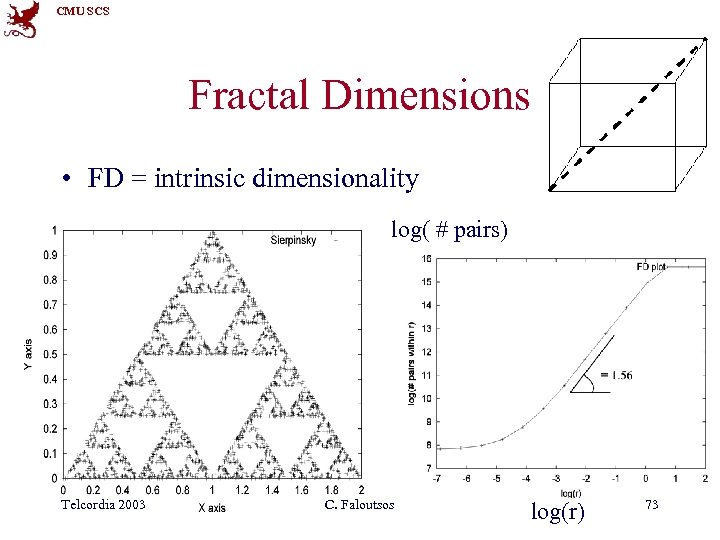CMU SCS Fractal Dimensions • FD = intrinsic dimensionality log( # pairs) Telcordia 2003 C. Faloutsos log(r) 73

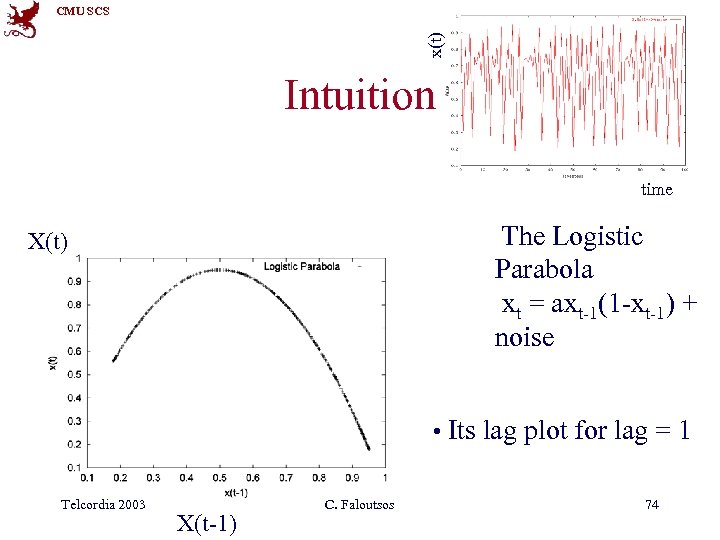x(t) CMU SCS Intuition time The Logistic Parabola xt = axt-1(1 -xt-1) + noise X(t) • Its lag plot for lag = 1 Telcordia 2003 X(t-1) C. Faloutsos 74

CMU SCS Intuition x(t) x(t-2) x(t-1) x(t) x(t-2) Telcordia 2003 x -1) (t C. Faloutsos x(t-2) ) -175 x(t

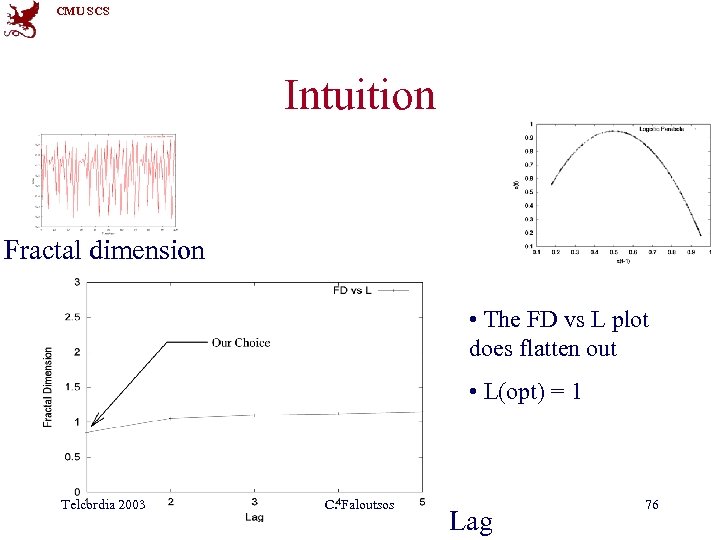CMU SCS Intuition Fractal dimension • The FD vs L plot does flatten out • L(opt) = 1 Telcordia 2003 C. Faloutsos Lag 76

CMU SCS Proposed Method Use Fractal Dimensions to find the optimal lag length L(opt) Fractal Dimension • epsilon Choose this Lag (L) Telcordia 2003 C. Faloutsos 77

CMU SCS Q 2: Choosing number of neighbors k • Manually (typically ~ 1 -10) Telcordia 2003 C. Faloutsos 78

CMU SCS Q 3: How to interpolate? How do we interpolate between the k nearest neighbors? A 3. 1: Average A 3. 2: Weighted average (weights drop with distance - how? ) Telcordia 2003 C. Faloutsos 79

CMU SCS Q 3: How to interpolate? A 3. 3: Using SVD - seems to perform best ([Sauer 94] - first place in the Santa Fe forecasting competition) xt Xt-1 Telcordia 2003 C. Faloutsos 80

CMU SCS Q 4: Any theory behind it? A 4: YES! Telcordia 2003 C. Faloutsos 81

CMU SCS Theoretical foundation • Based on the “Takens’ Theorem” [Takens 81] • which says that long enough delay vectors can do prediction, even if there are unobserved variables in the dynamical system (= diff. equations) Telcordia 2003 C. Faloutsos 82

CMU SCS Skip Theoretical foundation Example: Lotka-Volterra equations d. H/dt = r H – a H*P d. P/dt = b H*P – m P P H is count of prey (e. g. , hare) P is count of predators (e. g. , lynx) H Suppose only P(t) is observed (t=1, 2, …). Telcordia 2003 C. Faloutsos 83

CMU SCS Skip Theoretical foundation • But the delay vector space is a faithful reconstruction of the internal system state • So prediction in delay vector space is as good as prediction in state space P P(t) Telcordia 2003 H C. Faloutsos P(t-1) 84

CMU SCS Detailed Outline • Non-linear forecasting – Problem – Idea – How-to – Experiments – Conclusions Telcordia 2003 C. Faloutsos 85

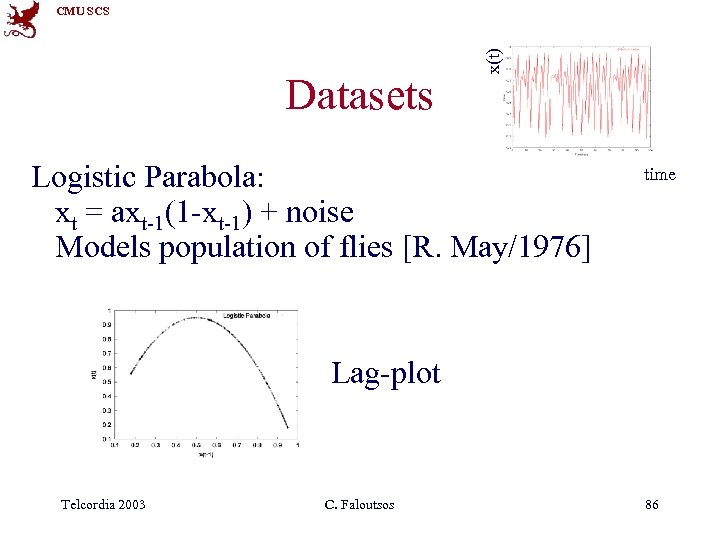Datasets x(t) CMU SCS Logistic Parabola: xt = axt-1(1 -xt-1) + noise Models population of flies [R. May/1976] time Lag-plot Telcordia 2003 C. Faloutsos 86

Datasets x(t) CMU SCS Logistic Parabola: xt = axt-1(1 -xt-1) + noise Models population of flies [R. May/1976] time Lag-plot ARIMA: fails Telcordia 2003 C. Faloutsos 87

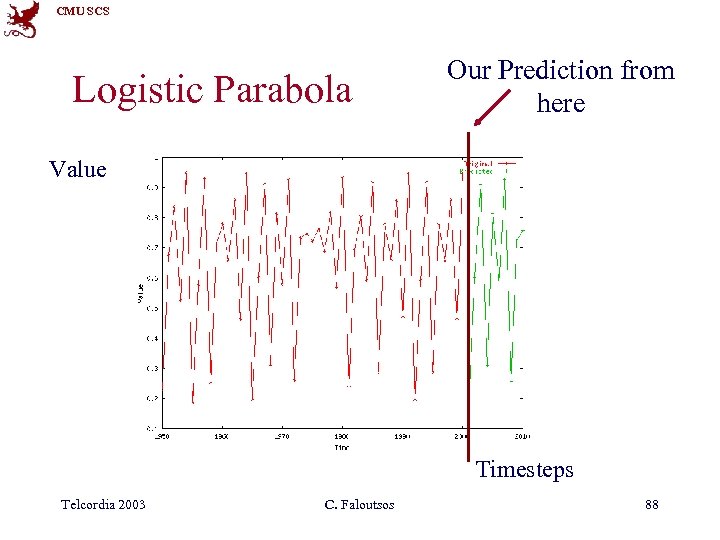CMU SCS Logistic Parabola Our Prediction from here Value Timesteps Telcordia 2003 C. Faloutsos 88

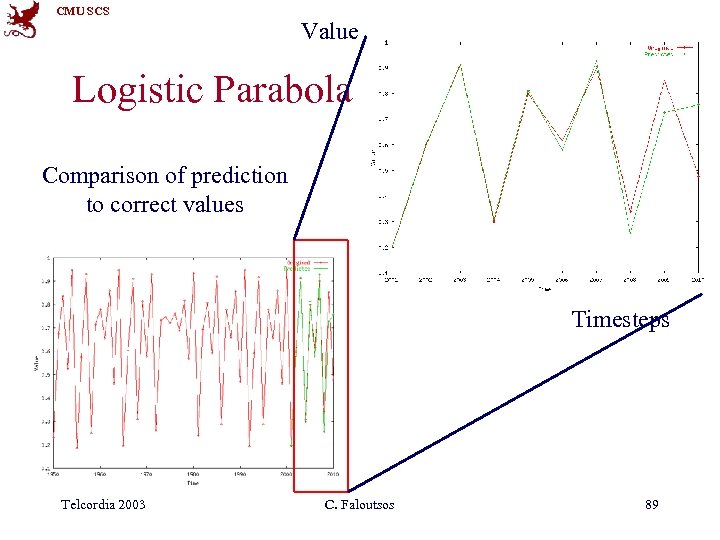CMU SCS Value Logistic Parabola Comparison of prediction to correct values Timesteps Telcordia 2003 C. Faloutsos 89

CMU SCS Value Datasets LORENZ: Models convection currents in the air dx / dt = a (y - x) dy / dt = x (b - z) - y dz / dt = xy - c z Telcordia 2003 C. Faloutsos 90

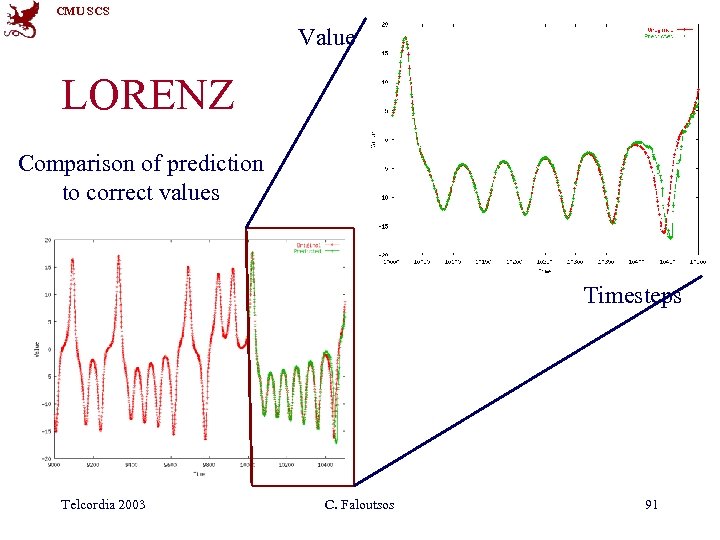CMU SCS Value LORENZ Comparison of prediction to correct values Timesteps Telcordia 2003 C. Faloutsos 91

CMU SCS Value Datasets • LASER: fluctuations in a Laser over time (used in Santa Fe competition) Telcordia 2003 C. Faloutsos Time 92

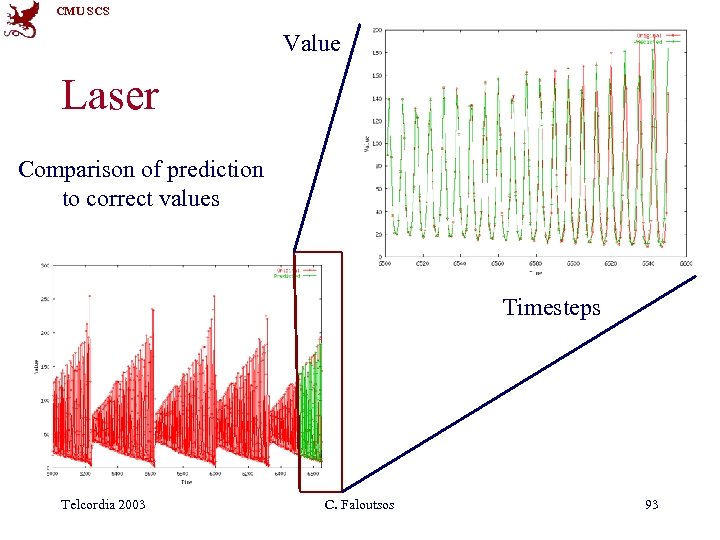CMU SCS Value Laser Comparison of prediction to correct values Timesteps Telcordia 2003 C. Faloutsos 93

CMU SCS Conclusions • Lag plots for non-linear forecasting (Takens’ theorem) • suitable for ‘chaotic’ signals Telcordia 2003 C. Faloutsos 94

CMU SCS Additional projects at CMU • Graph/Network mining • spatio-temporal mining - outliers Telcordia 2003 C. Faloutsos 95

CMU SCS Graph/network mining • Internet; web; gnutella P 2 P networks • Q: Any pattern? • Q: how to generate ‘realistic’ topologies? • Q: how to define/verify realism? Telcordia 2003 C. Faloutsos 96

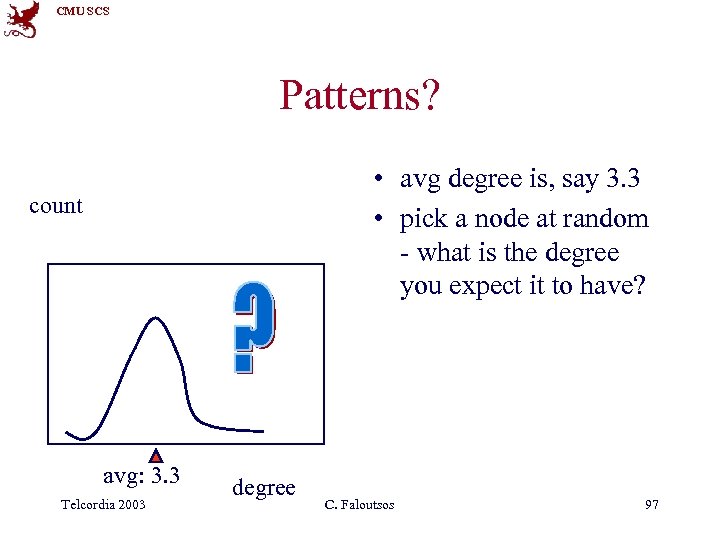CMU SCS Patterns? • avg degree is, say 3. 3 • pick a node at random - what is the degree you expect it to have? count avg: 3. 3 Telcordia 2003 degree C. Faloutsos 97

CMU SCS Patterns? • avg degree is, say 3. 3 • pick a node at random - what is the degree you expect it to have? • A: 1!! count avg: 3. 3 Telcordia 2003 degree C. Faloutsos 98

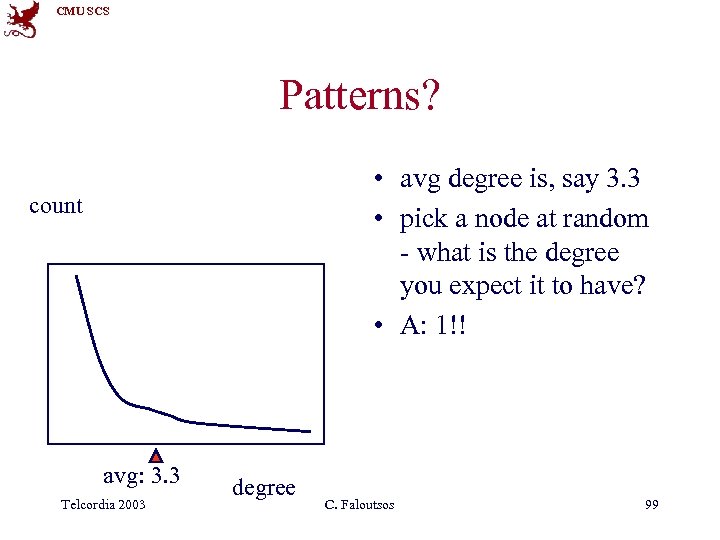CMU SCS Patterns? • avg degree is, say 3. 3 • pick a node at random - what is the degree you expect it to have? • A: 1!! count avg: 3. 3 Telcordia 2003 degree C. Faloutsos 99

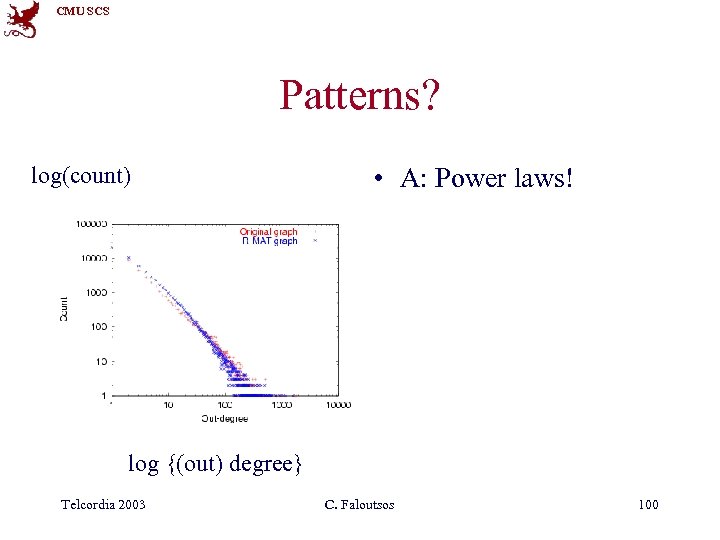CMU SCS Patterns? log(count) • A: Power laws! log {(out) degree} Telcordia 2003 C. Faloutsos 100

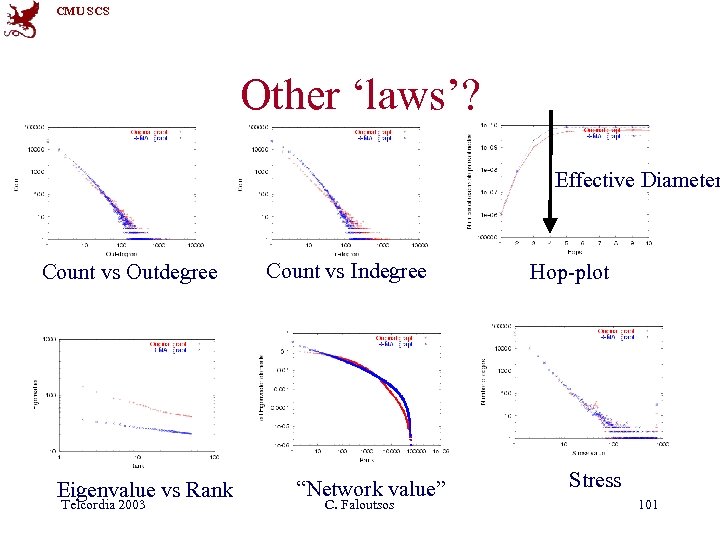CMU SCS Other ‘laws’? Effective Diameter Count vs Outdegree Eigenvalue vs Rank Telcordia 2003 Count vs Indegree “Network value” C. Faloutsos Hop-plot Stress 101

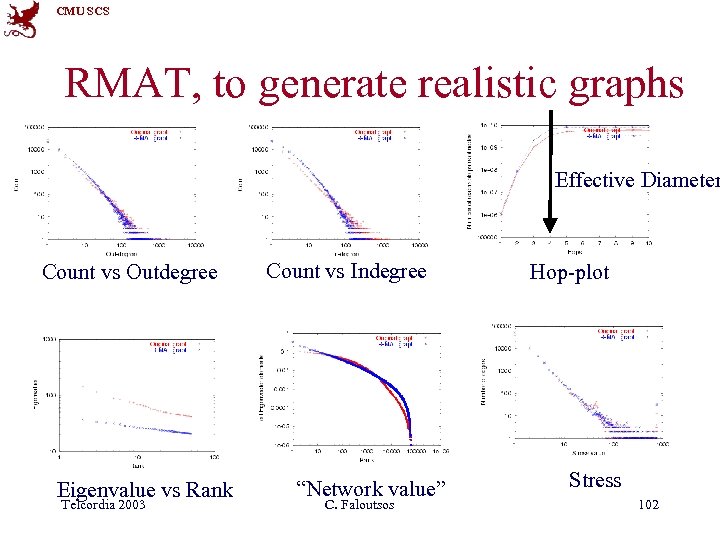CMU SCS RMAT, to generate realistic graphs Effective Diameter Count vs Outdegree Eigenvalue vs Rank Telcordia 2003 Count vs Indegree “Network value” C. Faloutsos Hop-plot Stress 102

CMU SCS Epidemic threshold? • one a real graph, will a (computer / biological) virus die out? (given – beta: probability that an infected node will infect its neighbor and – delta: probability that an infected node will recover NO Telcordia 2003 MAYBE YES C. Faloutsos 103

CMU SCS Additional projects • Graph mining • spatio-temporal mining - outliers Telcordia 2003 C. Faloutsos 105

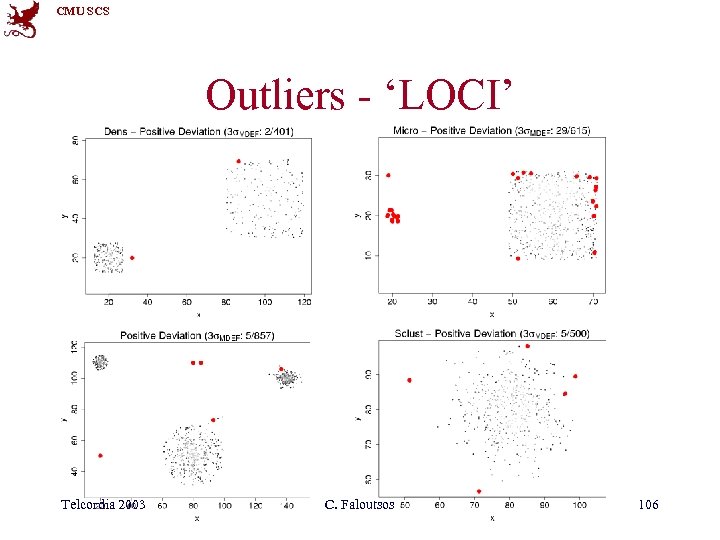CMU SCS Outliers - ‘LOCI’ Telcordia 2003 C. Faloutsos 106

CMU SCS Outliers - ‘LOCI’ • finds outliers quickly, • with no human intervention Telcordia 2003 C. Faloutsos 107

CMU SCS Conclusions • AWSOM for automatic, linear forecasting • MUSCLES for co-evolving sequences • F 4 for non-linear forecasting • Graph/Network topology: power laws and generators; epidemic threshold • LOCI for outlier detection Telcordia 2003 C. Faloutsos 108

CMU SCS Conclusions • Overarching theme: automatic discovery of patterns (outliers/rules) in – time sequences (sensors/streams) – graphs (computer/social networks) – multimedia (video, motion capture data etc) www. cs. cmu. edu/~christos@cs. cmu. edu Telcordia 2003 C. Faloutsos 109

CMU SCS Books • William H. Press, Saul A. Teukolsky, William T. Vetterling and Brian P. Flannery: Numerical Recipes in C, Cambridge University Press, 1992, 2 nd Edition. (Great description, intuition and code for DFT, DWT) • C. Faloutsos: Searching Multimedia Databases by Content, Kluwer Academic Press, 1996 (introduction to DFT, DWT) Telcordia 2003 C. Faloutsos 110

CMU SCS Books • George E. P. Box and Gwilym M. Jenkins and Gregory C. Reinsel, Time Series Analysis: Forecasting and Control, Prentice Hall, 1994 (the classic book on ARIMA, 3 rd ed. ) • Brockwell, P. J. and R. A. Davis (1987). Time Series: Theory and Methods. New York, Springer Verlag. Telcordia 2003 C. Faloutsos 111

CMU SCS Resources: software and urls • MUSCLES: Prof. Byoung-Kee Yi: http: //www. postech. ac. kr/~bkyi/ or christos@cs. cmu. edu • AWSOM & LOCI: spapadim@cs. cmu. edu • F 4, RMAT: deepay@cs. cmu. edu Telcordia 2003 C. Faloutsos 112

CMU SCS Additional Reading • [Chakrabarti+02] Deepay Chakrabarti and Christos Faloutsos F 4: Large-Scale Automated Forecasting using Fractals CIKM 2002, Washington DC, Nov. 2002. • [Chen+94] Chung-Min Chen, Nick Roussopoulos: Adaptive Selectivity Estimation Using Query Feedback. SIGMOD Conference 1994: 161 -172 • [Gilbert+01] Anna C. Gilbert, Yannis Kotidis and S. Muthukrishnan and Martin Strauss, Surfing Wavelets on Streams: One-Pass Summaries for Approximate Aggregate Queries, VLDB 2001 Telcordia 2003 C. Faloutsos 113

CMU SCS Additional Reading • Spiros Papadimitriou, Anthony Brockwell and Christos Faloutsos Adaptive, Hands-Off Stream Mining VLDB 2003, Berlin, Germany, Sept. 2003 • Spiros Papadimitriou, Hiroyuki Kitagawa, Phil Gibbons and Christos Faloutsos LOCI: Fast Outlier Detection Using the Local Correlation Integral ICDE 2003, Bangalore, India, March 5 - March 8, 2003. • Sauer, T. (1994). Time series prediction using delay coordinate embedding. (in book by Weigend and Gershenfeld, below) Addison-Wesley. Telcordia 2003 C. Faloutsos 114

CMU SCS Additional Reading • Takens, F. (1981). Detecting strange attractors in fluid turbulence. Dynamical Systems and Turbulence. Berlin: Springer-Verlag. • Yang Wang, Deepayan Chakrabarti, Chenxi Wang and Christos Faloutsos Epidemic Spreading in Real Networks: An Eigenvalue Viewpoint 22 nd Symposium on Reliable Distributed Computing (SRDS 2003) Florence, Italy, Oct. 6 -8, 2003 Telcordia 2003 C. Faloutsos 115

CMU SCS Additional Reading • Weigend, A. S. and N. A. Gerschenfeld (1994). Time Series Prediction: Forecasting the Future and Understanding the Past, Addison Wesley. (Excellent collection of papers on chaotic/non-linear forecasting, describing the algorithms behind the winners of the Santa Fe competition. ) • [Yi+00] Byoung-Kee Yi et al. : Online Data Mining for Co. Evolving Time Sequences, ICDE 2000. (Describes MUSCLES and Recursive Least Squares) Telcordia 2003 C. Faloutsos 116