CMU Apr 26 2010 Density Ratio Estimation A

CMU Apr. 26, 2010 Density Ratio Estimation: A New Versatile Tool for Machine Learning Department of Computer Science Tokyo Institute of Technology Masashi Sugiyama sugi@cs. titech. ac. jp http: //sugiyama-www. cs. titech. ac. jp/~sugi

Overview of My Talk (1) n Consider the ratio of two probability densities. n If the ratio is estimated, various machine learning problems can be solved! l Non-stationarity adaptation, domain adaptation, multi-task learning, outlier detection, change detection in time series, feature selection, dimensionality reduction, independent component analysis, conditional density estimation, classification, two-sample test 2

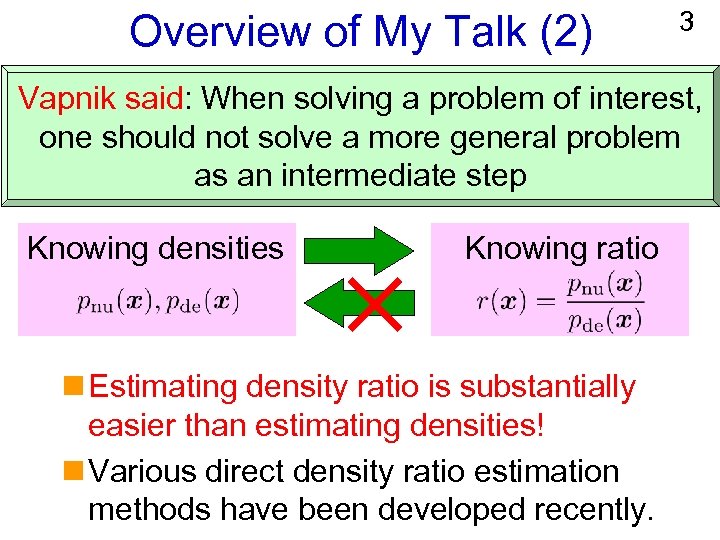Overview of My Talk (2) 3 Vapnik said: When solving a problem of interest, one should not solve a more general problem as an intermediate step Knowing densities Knowing ratio n Estimating density ratio is substantially easier than estimating densities! n Various direct density ratio estimation methods have been developed recently.

Organization of My Talk 1. Usage of Density Ratios: l Covariate shift adaptation l Outlier detection l Mutual information estimation l Conditional probability estimation 2. Methods of Density Ratio Estimation 4

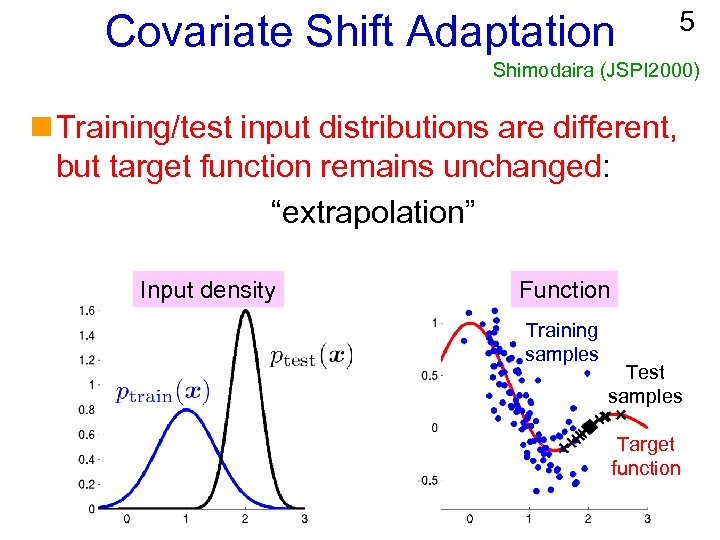Covariate Shift Adaptation 5 Shimodaira (JSPI 2000) n Training/test input distributions are different, but target function remains unchanged: “extrapolation” Input density Function Training samples Test samples Target function

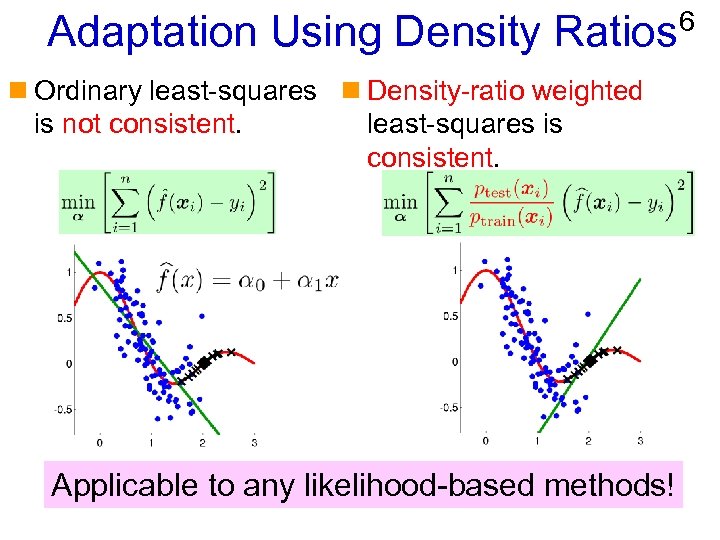Adaptation Using Density Ratios n Ordinary least-squares n Density-ratio weighted is not consistent. least-squares is consistent. Applicable to any likelihood-based methods! 6

Model Selection n Controlling bias-variance trade-off is important in covariate shift adaptation. No weighting: low-variance, high-bias l Density ratio weighting: low-bias, high-variance l n Density ratio weighting plays an important role for unbiased model selection: l Akaike information criterion (regular models) Shimodaira (JSPI 2000) l Subspace information criterion (linear models) Sugiyama & Müller (Stat&Dec. 2005) l Cross-validation (arbitrary models) Sugiyama, Krauledat & Müller (JMLR 2007) 7

Active Learning 8 n Covariate shift naturally occurs in active learning scenarios: l l is designed by users. is determined by environment. n Density ratio weighting plays an important role for low-bias active learning. l Population-based methods: l Pool-based methods: Wiens (JSPI 2000) Kanamori & Shimodaira (JSPI 2003) Sugiyama, (JMLR 2006) Kanamori, (Neuro. Comp 2007), Sugiyama & Nakajima (MLJ 2009)

Real-world Applications n Age prediction from faces (with NECsoft): l Illumination and angle change (KLS&CV) Ueki, Sugiyama & Ihara (ICPR 2010) n Speaker identification (with Yamaha): l Voice quality change (KLR&CV) Yamada, Sugiyama & Matsui (SP 2010) n Brain-computer interface: l Mental condition change (LDA&CV) Sugiyama, Krauledat & Müller (JMLR 2007) Li, Kambara, Koike & Sugiyama (IEEE-TBE 2010) 9

Real-world Applications (cont. ) 10 n Japanese text segmentation (with IBM): l Domain adaptation from general conversation to medicine (CRF&CV) こんな・失敗・は・ご・愛敬・だ・よ・ ． Tsuboi, Kashima, Hido, Bickel & Sugiyama (JIP 2008) n Semiconductor wafer alignment (with Nikon): l Optical marker allocation (AL) Sugiyama & Nakajima (MLJ 2009) n Robot control: l Dynamic motion update (KLS&CV) Hachiya, Akiyama, Sugiyama & Peters (NN 2009) Hachiya, Peters & Sugiyama (ECML 2009) l Optimal exploration (AL) Akiyama, Hachiya, & Sugiyama (NN 2010)

Organization of My Talk 1. Usage of Density Ratios: l Covariate shift adaptation l Outlier detection l Mutual information estimation l Conditional probability estimation 2. Methods of Density Ratio Estimation 11

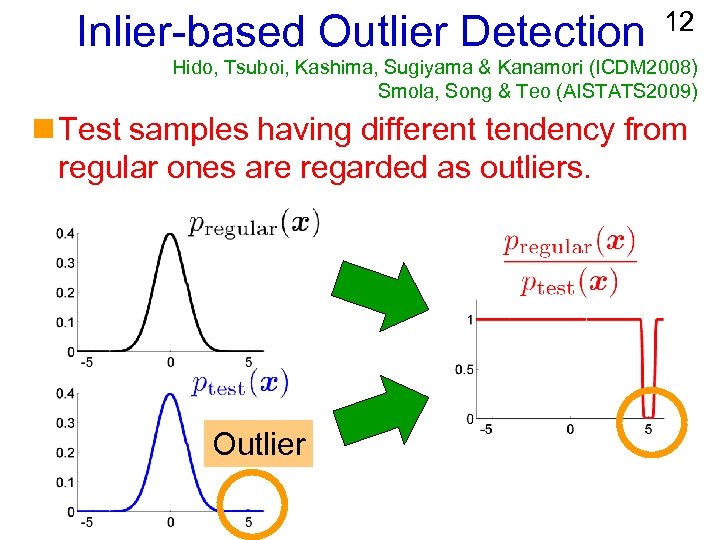Inlier-based Outlier Detection 12 Hido, Tsuboi, Kashima, Sugiyama & Kanamori (ICDM 2008) Smola, Song & Teo (AISTATS 2009) n Test samples having different tendency from regular ones are regarded as outliers. Outlier

Real-world Applications n Steel plant diagnosis (with JFE Steel) n Printer roller quality control (with Canon) Takimoto, Matsugu & Sugiyama (DMSS 2009) n Loan customer inspection (with IBM) Hido, Tsuboi, Kashima, Sugiyama & Kanamori (KAIS 2010) n Sleep therapy from biometric data Kawahara & Sugiyama (SDM 2009) 13

Organization of My Talk 1. Usage of Density Ratios: l Covariate shift adaptation l Outlier detection l Mutual information estimation l Conditional probability estimation 2. Methods of Density Ratio Estimation 14

Mutual Information Estimation 15 n Mutual information (MI): n MI as an independence measure: 　　and　　are statistically independent n MI can be approximated using density ratio: Suzuki, Sugiyama & Tanaka (ISIT 2009)

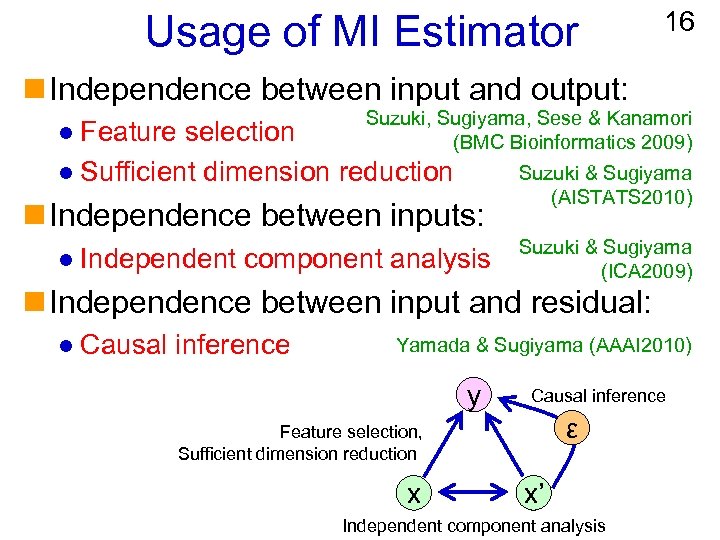Usage of MI Estimator 16 n Independence between input and output: Suzuki, Sugiyama, Sese & Kanamori (BMC Bioinformatics 2009) Feature selection l Sufficient dimension reduction l n Independence between inputs: l Independent component analysis Suzuki & Sugiyama (AISTATS 2010) Suzuki & Sugiyama (ICA 2009) n Independence between input and residual: l Causal inference Yamada & Sugiyama (AAAI 2010) y Causal inference ε Feature selection, Sufficient dimension reduction x x’ Independent component analysis

Organization of My Talk 1. Usage of Density Ratios: l Covariate shift adaptation l Outlier detection l Mutual information estimation l Conditional probability estimation 2. Methods of Density Ratio Estimation 17

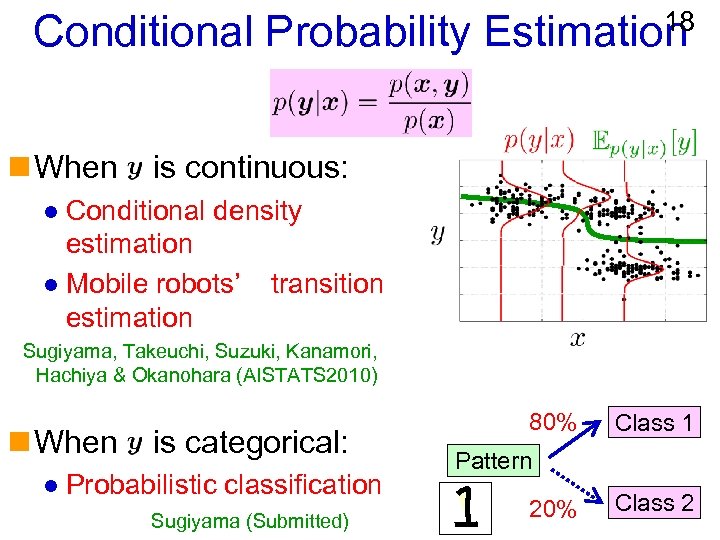18 Conditional Probability Estimation n When is continuous: Conditional density estimation l Mobile robots’ transition estimation l Sugiyama, Takeuchi, Suzuki, Kanamori, Hachiya & Okanohara (AISTATS 2010) n When l is categorical: Probabilistic classification Sugiyama (Submitted) 80% Class 1 Pattern 20% Class 2

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) D) E) Probabilistic Classification Approach Moment matching Approach Ratio matching Approach Comparison Dimensionality Reduction 19

Density Ratio Estimation n Density ratios are shown to be versatile. n In practice, however, the density ratio should be estimated from data. n Naïve approach: Estimate two densities separately and take their ratio 20

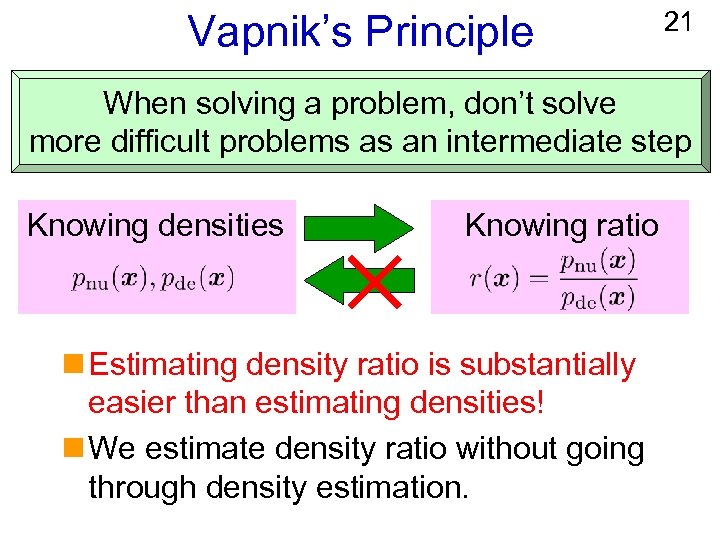Vapnik’s Principle 21 When solving a problem, don’t solve more difficult problems as an intermediate step Knowing densities Knowing ratio n Estimating density ratio is substantially easier than estimating densities! n We estimate density ratio without going through density estimation.

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) D) E) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach Comparison Dimensionality Reduction 22

Probabilistic Classification 23 n Separate numerator and denominator samples by a probabilistic classifier: n Logistic regression achieves the minimum asymptotic variance when model is correct. Qin (Biometrika 1998)

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) D) E) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach Comparison Dimensionality Reduction 24

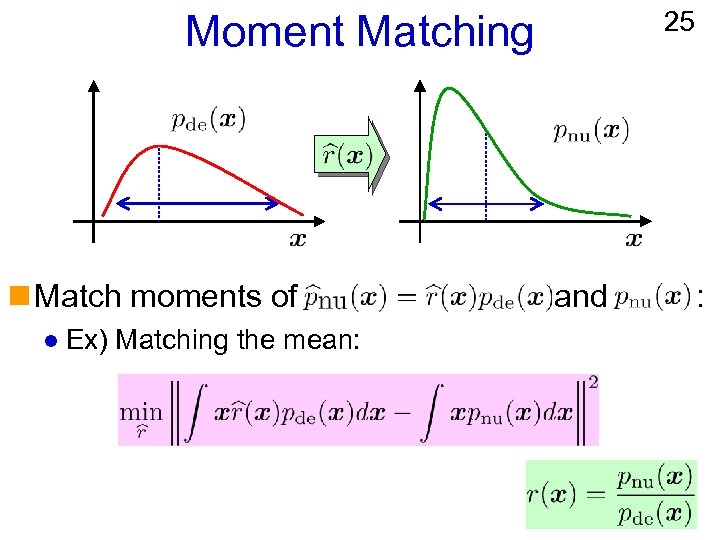25 Moment Matching n Match moments of l Ex) Matching the mean: and :

Kernel Mean Matching 26 Huang, Smola, Gretton, Borgwardt & Schölkopf (NIPS 2006) n Matching a finite number of moments does not yield the true ratio even asymptotically. n Kernel mean matching: All the moments are efficiently matched using Gaussian RKHS: Ratio values at samples can be estimated via quadratic program. l Variants for learning entire ratio function and other loss functions are also available. l Kanamori, Suzuki & Sugiyama (ar. Xiv 2009)

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach i. Kullback-Leibler Divergence ii. Squared Distance D) E) Comparison Dimensionality Reduction 27

Ratio Matching 28 Sugiyama, Suzuki & Kanamori (RIMS 2010) n Match a ratio model with true ratio under the Bregman divergence: (Constant is ignored) n Its empirical approximation is given by

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach i. Kullback-Leibler Divergence ii. Squared Distance D) E) Comparison Dimensionality Reduction 29

30 Kullback-Leibler Divergence (KL) Sugiyama, Nakajima, Kashima, von Bünau & Kawanabe (NIPS 2007) Nguyen, Wainwright & Jordan (NIPS 2007) n Put . Then BR yields n For a linear model minimization of KL is convex. , (ex. Gauss kernel)

Properties 31 Nguyen, Wainwright & Jordan (NIPS 2007) Sugiyama, Suzuki, Nakajima, Kashima, von Bünau & Kawanabe (AISM 2008) n Parametric case: l Learned parameter converge to the optimal value with order. n Non-parametric case: l Learned function converges to the optimal function with order slightly slower than (depending on the covering number or the bracketing entropy of the function class).

Experiments 32 n Setup: d-dim. Gaussian with covariance identity and l Denominator: mean (0, 0, 0, …, 0) l Numerator: mean (1, 0, 0, …, 0) n Ratio of kernel density estimators (RKDE): Estimate two densities separately and take ratio. l Gaussian width is chosen by CV. l n KL method: Estimate density ratio directly. l Gaussian width is chosen by CV. l

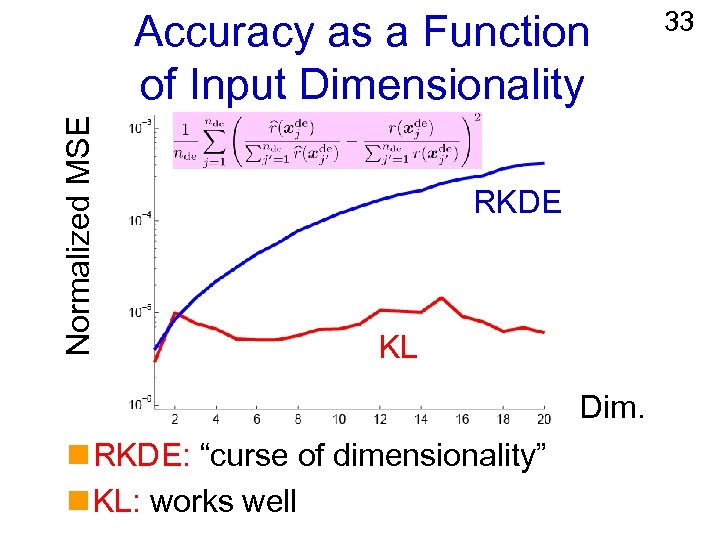Normalized MSE Accuracy as a Function of Input Dimensionality RKDE KL Dim. n RKDE: “curse of dimensionality” n KL: works well 33

Variations n EM algorithms for KL with l Log-linear models Tsuboi, Kashima, Hido, Bickel & Sugiyama (JIP 2009) l Gaussian mixture models Yamada & Sugiyama (IEICE 2009) l Probabilistic PCA mixture models Yamada, Sugiyama, Wichern & Jaak (Submitted) are also available. 34

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach i. Kullback-Leibler Divergence ii. Squared Distance D) E) Comparison Dimensionality Reduction 35

Squared Distance (SQ) 36 Kanamori, Hido & Sugiyama (JMLR 2009) n Put . Then BR yields n For a linear model minimizer of SQ is analytic: n Computationally efficient! ,

Properties 37 Kanamori, Hido & Sugiyama (JMLR 2009) Kanamori, Suzuki & Sugiyama (ar. Xiv 2009) n Optimal parametric/non-parametric rates of convergence are achieved. n Leave-one-out cross-validation score can be computed analytically. n SQ has the smallest condition number. n Analytic solution allows computation of the derivative of mutual information estimator: Sufficient dimension reduction l Independent component analysis l Causal inference l

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) D) E) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach Comparison Dimensionality Reduction 38

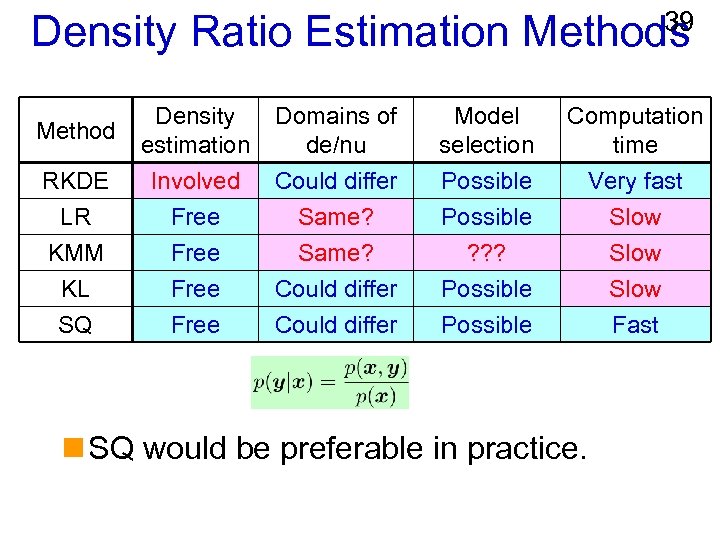39 Density Ratio Estimation Methods RKDE LR Density estimation Involved Free Domains of de/nu Could differ Same? Model selection Possible Computation time Very fast Slow KMM KL SQ Free Same? Could differ ? ? ? Possible Slow Fast Method n SQ would be preferable in practice.

Organization of My Talk 1. Usage of Density Ratios 2. Methods of Density Ratio Estimation: A) B) C) D) E) Probabilistic Classification Approach Moment Matching Approach Ratio Matching Approach Comparison Dimensionality Reduction 40

41 Direct Density Ratio Estimation with Dimensionality Reduction (D 3) n Directly density ratio estimation without going through density estimation is promising. n However, for high-dimensional data, density ratio estimation is still challenging. n We combine direct density ratio estimation with dimensionality reduction!

42 Hetero-distributional Subspace (HS) n Key assumption: and are different only in a subspace (called HS). HS : Full-rank and orthogonal n This allows us to estimate the density ratio only within the low-dimensional HS!

43 HS Search Based on Supervised Dimension Reduction Sugiyama, Kawanabe & Chui (NN 2010) n In HS, and are different, so and would be separable. n We may use any supervised dimension reduction method for HS search. n Local Fisher discriminant analysis (LFDA): Can handle within-class multimodality l No limitation on reduced dimensions l Analytic solution available l Sugiyama (JMLR 2007)

44 Pros and Cons of Supervised Dimension Reduction Approach n Pros: l SQ+LFDA gives analytic solution for D 3. n Cons: l Rather restrictive implicit assumption that and are independent. l Separability does not always lead to HS (e. g. , two overlapped, but different densities) Separable HS

Characterization of HS 45 Sugiyama, Hara, von Bünau, Suzuki, Kanamori & Kawanabe (SDM 2010) n HS is given as the maximizer of the Pearson divergence : n Thus, we can identify HS by finding maximizer of PE with respect to. n PE can be analytically approximated by SQ!

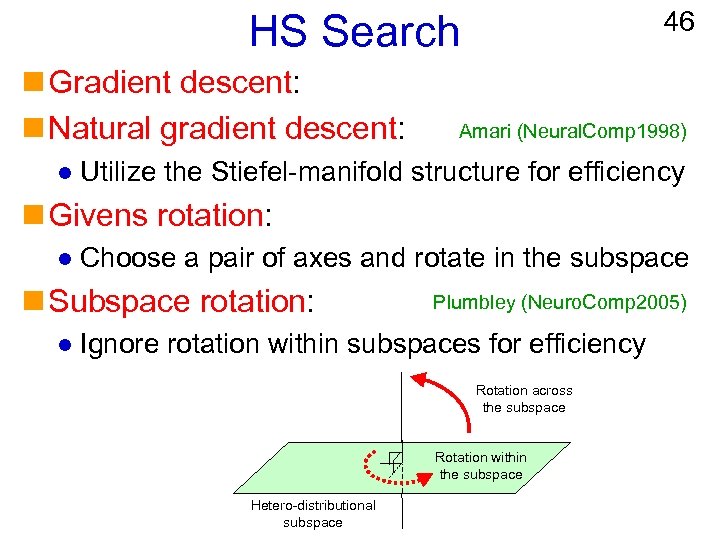46 HS Search n Gradient descent: n Natural gradient descent: l Amari (Neural. Comp 1998) Utilize the Stiefel-manifold structure for efficiency n Givens rotation: l Choose a pair of axes and rotate in the subspace n Subspace rotation: l Plumbley (Neuro. Comp 2005) Ignore rotation within subspaces for efficiency Rotation across the subspace Rotation within the subspace Hetero-distributional subspace

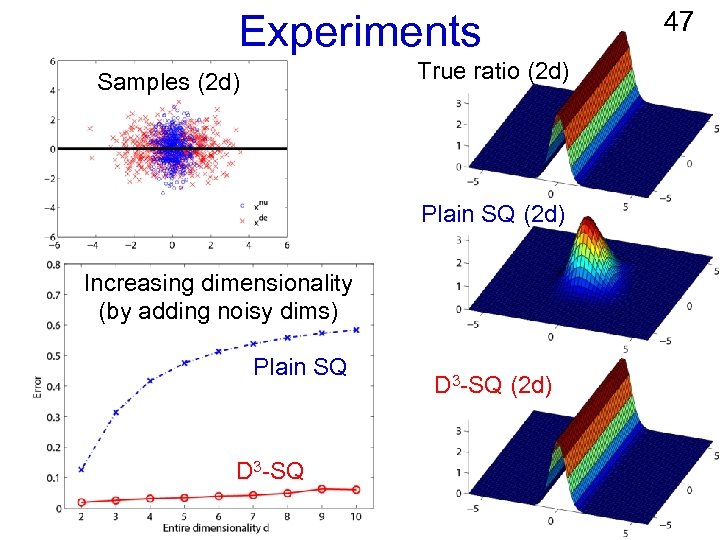Experiments True ratio (2 d) Samples (2 d) Plain SQ (2 d) Increasing dimensionality (by adding noisy dims) Plain SQ D 3 -SQ (2 d) 47

Conclusions 48 n Many ML tasks can be solved via density ratio estimation: l Non-stationarity adaptation, domain adaptation, multi-task learning, outlier detection, change detection in time series, feature selection, dimensionality reduction, independent component analysis, conditional density estimation, classification, two-sample test n Directly estimating density ratios without going through density estimation is the key. l LR, KMM, KL, SQ, and D 3.

Books 49 n Quiñonero-Candela, Sugiyama, Schwaighofer & Lawrence (Eds. ), Dataset Shift in Machine Learning, MIT Press, 2009. n Sugiyama, von Bünau, Kawanabe & Müller, Covariate Shift Adaptation in Machine Learning, MIT Press (coming soon!) n Sugiyama, Suzuki & Kanamori, Density Ratio Estimation in Machine Learning, Cambridge University Press (coming soon!)

The World of Density Ratios 50 Real-world applications: Brain-computer interface, Robot control, Image understanding, Speech recognition, Natural language processing, Bioinformatics Machine learning algorithms: Covariate shift adaptation, Outlier detection, Conditional probability estimation, Mutual information estimation Density ratio estimation: Fundamental algorithms (LR, KMM, KL, SQ) Large-scale, High-dimensionality, Stabilization, Robustification Theoretical analysis: Convergence, Information criteria, Numerical stability