bea07d8f3ce3191753ca8d08bde2d856.ppt
- Количество слайдов: 30

CMSC 341 Binary Heaps Priority Queues

Priority Queues Priority: some property of an object that allows it to be prioritized WRT other objects (of the same type) Priority Queue: homogeneous collection of Comparables with the following operations (duplicates are allowed) – – – – void insert (const Comparable &x) void delete. Min() void delete. Min ( Comparable & min) const Comparable &find. Min() const Construct from set of initial values bool is. Empty() const bool is. Full() const void make. Empty() 2

Priority Queue Applications Printer management: the shorter document on the printer queue, the higher its priority. Jobs queue: users’ tasks are given priorities. System priority high. Simulations Sorting 3

Possible Implementations Use sorted list. Sort by priority upon insertion. – find. Min() --> Itr. retrieve() – insert() --> list. insert() – delete. Min() --> list. delete(1) Use ordinary BST – find. Min() --> tree. find. Min() – insert() --> tree. insert() – delete. Min() --> tree. delete(tree. find. Min()) Use balanced BST – guaranteed O(lg n) for AVL, Red-Black 4

Binary Heap A binary heap is a CBT with the further property that at every vertex neither child is smaller than the vertex, called partial ordering. Every path from the root to a leaf visits vertices in a nondecreasing order. 5

Binary Heap Properties For a node at index i – its left child is at index 2 i – its right child is at index 2 i+1 – its parent is at index i/2 No pointer storage Fast computation of 2 i and i/2 i << 1 = 2 i i >> 1 = i/2 6

Binary Heap Performance – – construction find. Min insert delete. Min O(n) O(1) O(lg n) Heap efficiency results, in part, from the implementation – conceptually a binary tree – implementation in an array (in level order), root at index 1 7

Binary. Heap. H template <class Comparable> class Binary Heap { public: explicit Binary. Heap(int capacity = BIG); bool is. Empty() const; bool is. Full() const; const Comparable & find. Min() const; void insert (const Comparable & x); void delete. Min(Comparable & min_item); void make. Empty(); private: int current. Size; vector<Comparable> array; void build. Heap(); void percolate. Down(int hole); }; 8

Binary. Heap. C template <class Comparable> const Comparable & Binary. Heap: : find. Min( ) { if ( is. Empty( ) ) throw Underflow( ); return array[1]; } 9

Insert Operation Must maintain – CBT property (heap shape): • easy, just insert new element at the right of the array – Heap order • could be wrong after insertion if new element is smaller than its ancestors • continuously swap the new element with its parent until parent is not greater than it – called sift up or percolate up Performance O(lg n) worst case because height of CBT is O(lg n) 10

Binary. Heap. C (cont) template <class Comparable> void Binary. Heap<Comparable>: : insert(const Comparable & x) { if (is. Full()) throw Over. Flow(); int hole = ++current. Size; // percolate up for (; hole > 1 && x < array[hole/2]; hole /= 2) array[hole] = array[hole/2]; // put x in hole array[hole] = x; } 11

Deletion Operation Steps – remove min element (the root) – maintain heap shape – maintain heap order To maintain heap shape, actual vertex removed is last one – replace root value with value from last vertex and delete last vertex – sift-down the new root value • continually exchange value with the smaller child until no child is smaller 12

Binary. Heap. C (cont) template <class Comparable> void Binary. Heap<Comparable>: : delete. Min(Comparable & min. Item) { if ( is. Empty( ) ) throw Underflow( ); min. Item = array[1]; array[1] = array[current. Size--]; percolate. Down(1); } 13

Binary. Heap. C (cont) template <class Comparable> void Binary. Heap<Comparable>: : percolate. Down(int hole) { int child; Comparable tmp = array[hole]; for (; hole * 2 <= current. Size; hole = child) { child= hole * 2; if (child != current. Size && array[child + 1] < array[ child ] ) child++; if (array [child] < tmp) array[ hole ] = array[ child ]; else break; } array[hole] = tmp; } 14

Constructing a Binary Heap A BH can be constructed in O(n) time. Suppose an array in arbitrary order. It can be put in heap order in O(n) time. – Create the array and store n elements in it in arbitrary order. O(n) – Heapify the array • start at vertex i = n/2 – percolate. Down(i) • repeat for all vertices down to i 15

Binary. Heap. C (cont) template <class Comparable> void Binary. Heap<Comparable>: : build. Heap( ) { for(int i = current. Size/2; i >0; i--) percolate. Down(i); } 16

Performance of Construction A CBT has 2 h-1 vertices on level h-1. On level h-l, at most 1 swap is needed per node. On level h-2, at most 2 swaps are needed. … On level 0, at most h swaps are needed. Number of swaps = S = 2 h*0 + 2 h-1*1 + 2 h-2*2 + … + 20*h = = h(2 h+1 -1) - ((h-1)2 h+1+2) = 2 h+1(h-(h-1))-h-2 = 2 h+1 -h-2 17

Performance of Construction (cont) But 2 h+1 -h-2 = O(2 h) But n = 1 + 2 + 4 + … + 2 h = Therefore, n = O(2 h) So S = O(n) A heap of n vertices can be built in O(n) time. 18

Heap Sort Given n values, can sort in O(n log n) time (in place). – Insert values into array -- O(n) – heapify -- O(n) – repeatedly delete min -- O(lg n) n times Using a min heap, this code sorts in reverse order. With a max heap, it sorts in normal order. for (i = n-1; i >= 1; i--) { x =find. Min(); delete. Min(); A[i+1] = x; } 19

Limitations Binary heaps support insert, find. Min, delete. Min, and construct efficiently. They do not efficiently support the meld or merge operation in which 2 PQs are merged into one. If P 1 and P 2 are of size n 1 and n 2, then the merge is in O(n 1 + n 2) 20

Leftist Heap Supports – find. Min – delete. Min – insert – construct – merge -- O(1) -- O(lg n) -- O(n) -- O(lg n) 21

Leftist Tree A LT is a binary tree in which at each vertex v, the path length, dr, from v’s right child to the nearest non-full vertex is not larger than that from the vertex’s left child to the nearest non-full vertex. An important property of leftist trees: – At every vertex, the shortest path to a non-full vertex is along the rightmost path. – Suppose this was not true. Then, at the same vertex the path on the left would be shorter than the path on the right. 22

Leftist Heap A leftist heap is a leftist tree in which the values in the vertices obey heap order (the tree is partially ordered). Since a LH is not necessarily a CBT we do not implement it in an array. An explicit tree implementation is used. Operations – find. Min -- return root value, same as BH – delete. Min -- done using meld operation – insert -- done using meld operation – construct -- done using meld operation 23

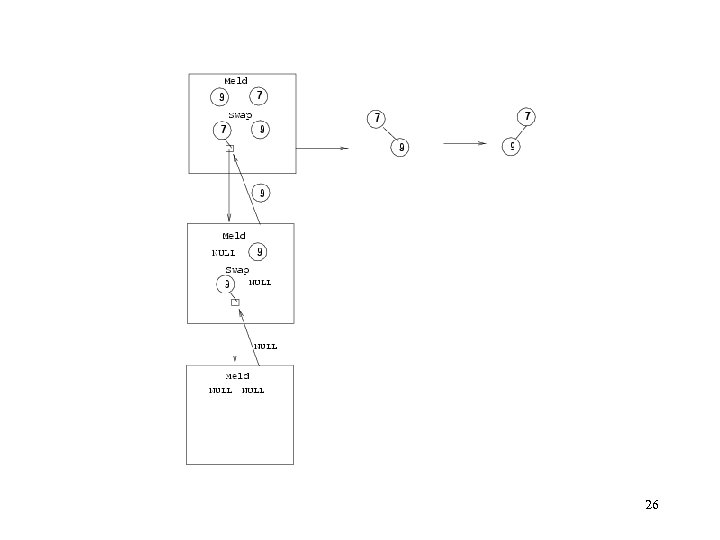
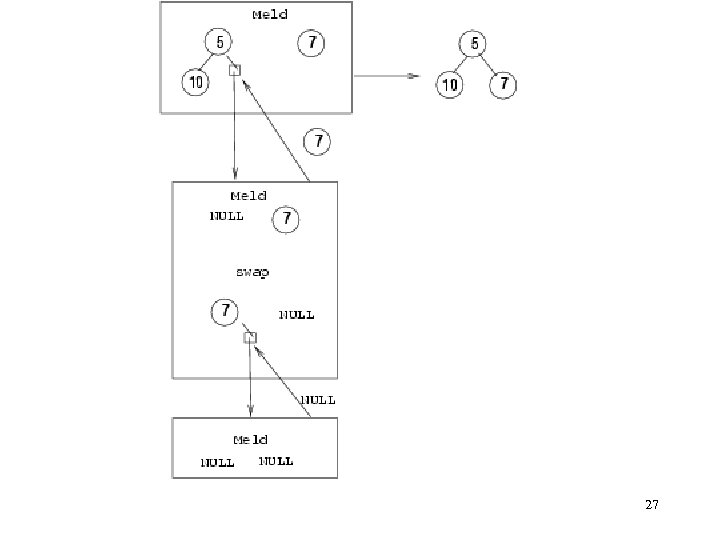
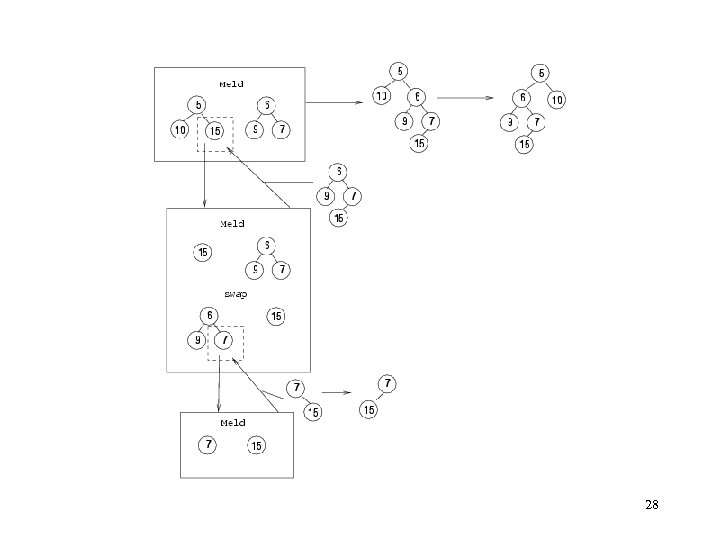
Meld Algorithm: Meld (H 1, H 2) { if (!root(H 1) || (root_value(H 1) > root_value(H 2) ) swap (H 1, H 2) if (root(H 1) != NULL)) right(H 1) <-- Meld(right(H 1), H 2) if (left_length(H 1) < right_length(H 1) swap(left(H 1), right(H 1); } 24

Meld (cont) Performance: O(lg n) – the rightmost path of each tree has at most lg(n+1) vertices. So O(lg n) vertices will be involved. 25
26
27
28

Leftist Heap Operations Other operations implemented in terms of Meld – insert (item) • make item into a 1 -vertex LH, X • Meld(*this, X) – delete. Min • Meld(left subtree, right subtree) – construct from N items • make N LH from the N values, one element in each • meld each in – one at a time : – use queue and build pairwise : 29

LH Construct Algorithm: – make N heaps each with one data value – Queue Q; – for (I=1; I <= N; I++) Q. Enqueue(Hi); – Heap H = Q. Dequeue(); – while (!Q. Is. Empty()) Q. Enqueue(meld(H, Q. Dequeue()); H = Q. Dequeue(); 30
bea07d8f3ce3191753ca8d08bde2d856.ppt