CMPUT 429 CMPE 382 Winter 2001 Adapted from 1 17 01

CMPUT 429/CMPE 382 Winter 2001 (Adapted from 1/17/01 Topic. C: I/O David A. Patterson’s CS 252, Spring 2001 Lecture Slides) CMPUT 429/CMPE 382 Amaral

Motivation: Who Cares About I/O? • CPU Performance: Improves 60% per year • I/O system performance limited by mechanical delays (disk I/O) improves less than 10% per year (IO per sec) • Amdahl's Law: system speed-up limited by the slowest part! 10% IO & 10 x CPU => 5 x Performance (lose 50% of CPU gain) 10% IO & 100 x CPU => 10 x Performance (lose 90% of CPU gain) • I/O bottleneck: Diminishing fraction of time in CPU Diminishing value of faster CPUs 1/17/01 CMPUT 429/CMPE 382 Amaral

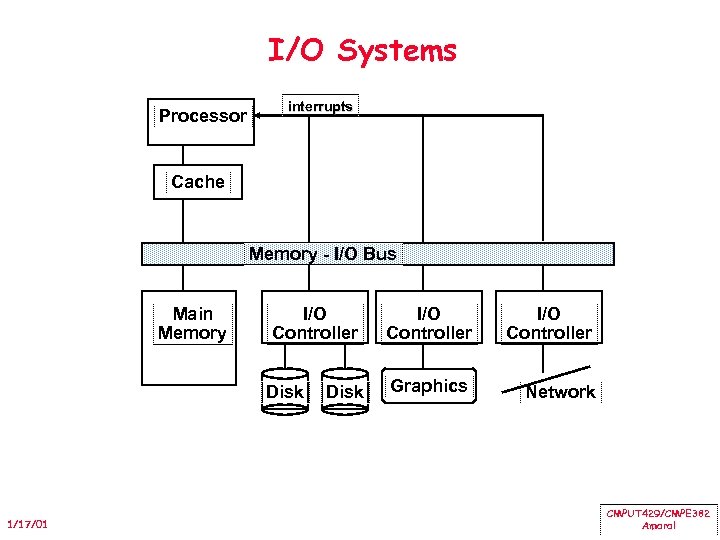I/O Systems Processor interrupts Cache Memory - I/O Bus Main Memory I/O Controller Disk 1/17/01 Disk I/O Controller Graphics Network CMPUT 429/CMPE 382 Amaral

Outline • • • 1/17/01 Disk Basics Disk History Disk options in 2000 Disk fallacies and performance Tapes RAID CMPUT 429/CMPE 382 Amaral

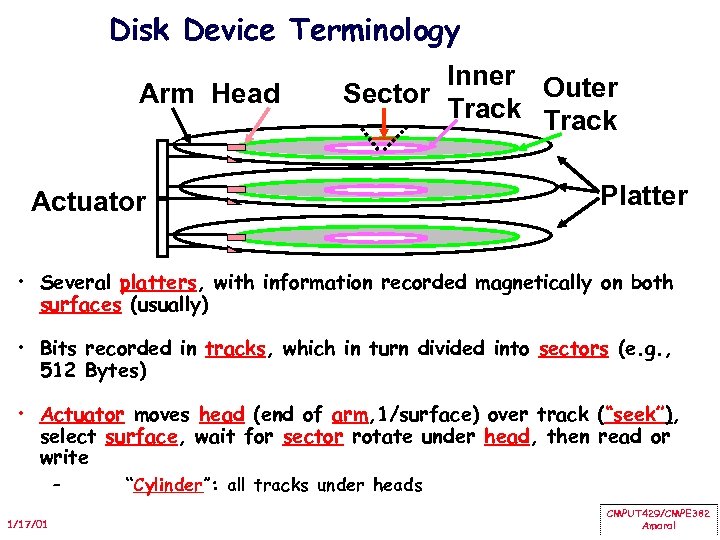Disk Device Terminology Arm Head Inner Outer Sector Track Actuator Platter • Several platters, with information recorded magnetically on both surfaces (usually) • Bits recorded in tracks, which in turn divided into sectors (e. g. , 512 Bytes) • Actuator moves head (end of arm, 1/surface) over track (“seek”), select surface, wait for sector rotate under head, then read or write – 1/17/01 “Cylinder”: all tracks under heads CMPUT 429/CMPE 382 Amaral

Photo of Disk Head, Arm, Actuator Spindle Arm 1/17/01 { Actuator Head Platters (12) CMPUT 429/CMPE 382 Amaral

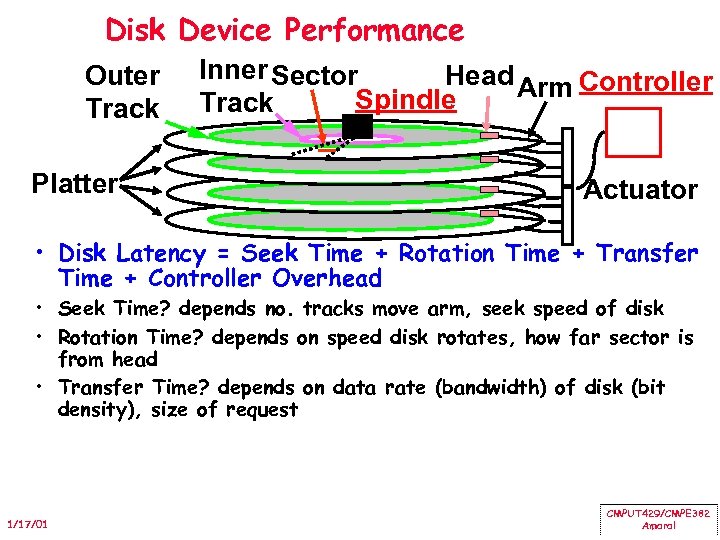Disk Device Performance Outer Track Platter Inner Sector Head Arm Controller Spindle Track Actuator • Disk Latency = Seek Time + Rotation Time + Transfer Time + Controller Overhead • Seek Time? depends no. tracks move arm, seek speed of disk • Rotation Time? depends on speed disk rotates, how far sector is from head • Transfer Time? depends on data rate (bandwidth) of disk (bit density), size of request 1/17/01 CMPUT 429/CMPE 382 Amaral

Disk Device Performance • Average distance sector from head? • 1/2 time of a rotation – 10000 Revolutions Per Minute 166. 67 Rev/sec – 1 revolution = 1/ 166. 67 sec 6. 00 milliseconds – 1/2 rotation (revolution) 3. 00 ms • Average no. tracks move arm? – Sum all possible seek distances from all possible tracks / # possible » Assumes average seek distance is random – Disk industry standard benchmark 1/17/01 CMPUT 429/CMPE 382 Amaral

Data Rate: Inner vs. Outer Tracks • To keep things simple, orginally kept same number of sectors per track – Since outer track longer, lower bits per inch • Competition decided to keep BPI the same for all tracks (“constant bit density”) More capacity per disk More of sectors per track towards edge Since disk spins at constant speed, outer tracks have faster data rate • Bandwidth outer track 1. 7 X inner track! – Inner track highest density, outer track lowest, so not really constant – 2. 1 X length of track outer / inner, 1. 7 X bits outer / inner 1/17/01 CMPUT 429/CMPE 382 Amaral

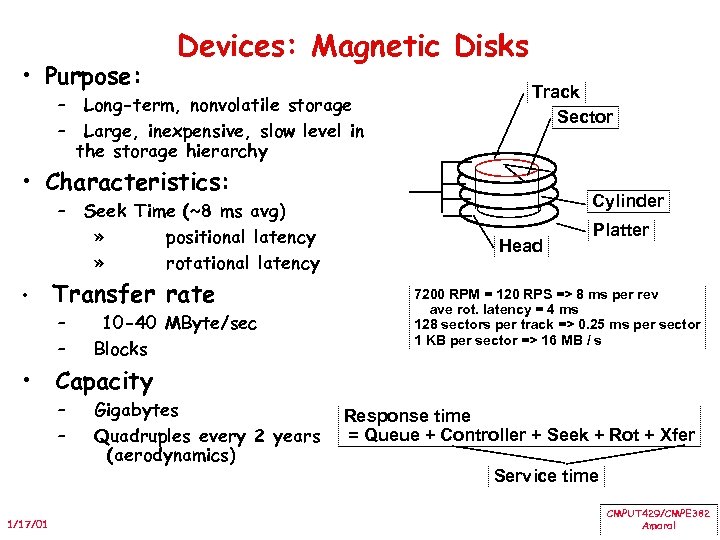• Purpose: Devices: Magnetic Disks – Long-term, nonvolatile storage – Large, inexpensive, slow level in the storage hierarchy Track Sector • Characteristics: – Seek Time (~8 ms avg) » positional latency » rotational latency • Transfer rate – – 10 -40 MByte/sec Blocks Cylinder Head Platter 7200 RPM = 120 RPS => 8 ms per rev ave rot. latency = 4 ms 128 sectors per track => 0. 25 ms per sector 1 KB per sector => 16 MB / s • Capacity – – 1/17/01 Gigabytes Quadruples every 2 years (aerodynamics) Response time = Queue + Controller + Seek + Rot + Xfer Service time CMPUT 429/CMPE 382 Amaral

Disk Performance Model /Trends • Capacity + 100%/year (2 X / 1. 0 yrs) • Transfer rate (BW) + 40%/year (2 X / 2. 0 yrs) • Rotation + Seek time – 8%/ year (1/2 in 10 yrs) • MB/$ > 100%/year (2 X / 1. 0 yrs) Fewer chips + areal density 1/17/01 CMPUT 429/CMPE 382 Amaral

State of the Art: Barracuda 180 Track Sector Cylinder Track Arm Platter Head Buffer Latency = Queuing Time + Controller time + per access Seek Time + + Rotation Time + per byte Size / Bandwidth { source: www. seagate. com 1/17/01 – 181. 6 GB, 3. 5 inch disk – 12 platters, 24 surfaces – 24, 247 cylinders – 7, 200 RPM; (4. 2 ms avg. latency) – 7. 4/8. 2 ms avg. seek (r/w) – 64 to 35 MB/s (internal) – 0. 1 ms controller time – 10. 3 watts (idle) CMPUT 429/CMPE 382 Amaral

Disk Performance Example (will fix later) • Calculate time to read 64 KB (128 sectors) for Barracuda 180 X using advertised performance; sector is on outer track Disk latency = average seek time + average rotational delay + transfer time + controller overhead = 7. 4 ms + 0. 5 * 1/(7200 RPM) + 64 KB / (65 MB/s) + 0. 1 ms = 7. 4 ms + 0. 5 /(7200 RPM/(60000 ms/M)) + 64 KB / (65 KB/ms) + 0. 1 ms = 7. 4 + 4. 2 + 1. 0 + 0. 1 ms = 12. 7 ms 1/17/01 CMPUT 429/CMPE 382 Amaral

Areal Density • Bits recorded along a track – Metric is Bits Per Inch (BPI) • Number of tracks per surface – Metric is Tracks Per Inch (TPI) • Disk Designs Brag about bit density per unit area – Metric is Bits Per Square Inch – Called Areal Density – Areal Density = BPI x TPI 1/17/01 CMPUT 429/CMPE 382 Amaral

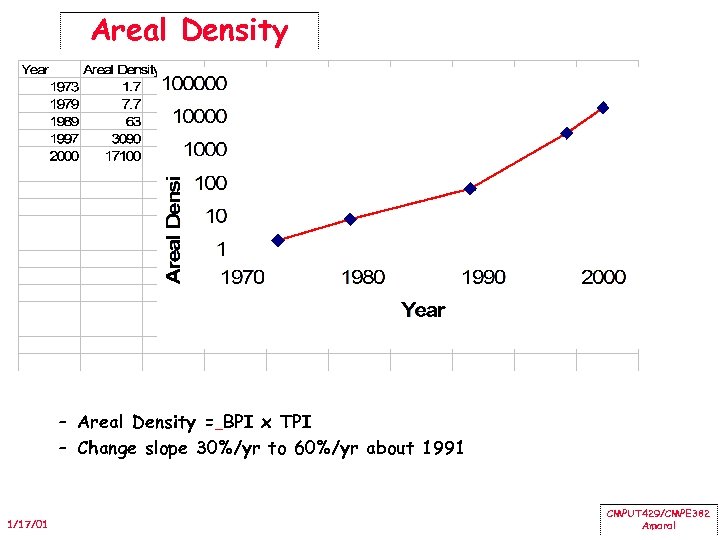Areal Density – Areal Density = BPI x TPI – Change slope 30%/yr to 60%/yr about 1991 1/17/01 CMPUT 429/CMPE 382 Amaral

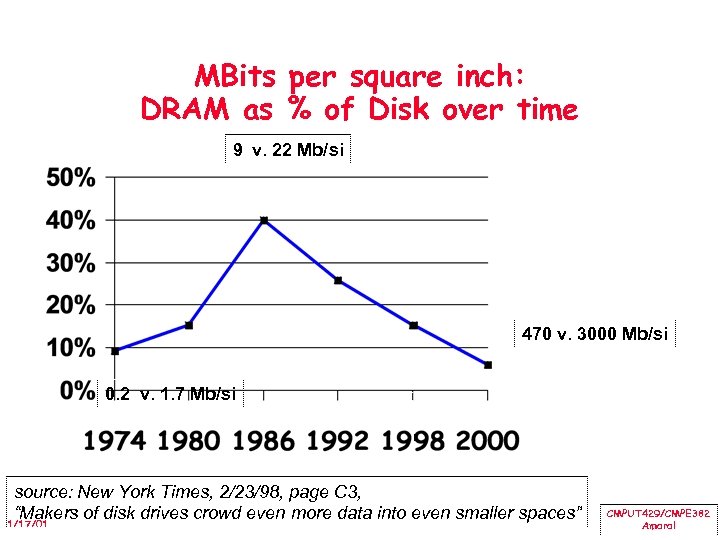MBits per square inch: DRAM as % of Disk over time 9 v. 22 Mb/si 470 v. 3000 Mb/si 0. 2 v. 1. 7 Mb/si source: New York Times, 2/23/98, page C 3, “Makers of disk drives crowd even more data into even smaller spaces” 1/17/01 CMPUT 429/CMPE 382 Amaral

Historical Perspective • 1956 IBM Ramac — early 1970 s Winchester – Developed for mainframe computers, proprietary interfaces – Steady shrink in form factor: 27 in. to 14 in • Form factor and capacity drives market, more than performance • 1970 s: Mainframes 14 inch diameter disks • 1980 s: Minicomputers, Servers 8”, 5 1/4” diameter • PCs, workstations Late 1980 s/Early 1990 s: – Mass market disk drives become a reality » industry standards: SCSI, IPI, IDE – Pizzabox PCs 3. 5 inch diameter disks – Laptops, notebooks 2. 5 inch disks – Palmtops didn’t use disks, so 1. 8 inch diameter disks didn’t make it • 2000 s: 1/17/01 – 1 inch for cameras, cell phones? CMPUT 429/CMPE 382 Amaral

Disk History Data density Mbit/sq. in. Capacity of Unit Shown Megabytes 1973: 1. 7 Mbit/sq. in 140 MBytes 1979: 7. 7 Mbit/sq. in 2, 300 MBytes source: New York Times, 2/23/98, page C 3, “Makers of disk drives crowd even more data into even smaller spaces” 1/17/01 CMPUT 429/CMPE 382 Amaral

Disk History 1989: 63 Mbit/sq. in 60, 000 MBytes 1997: 1450 Mbit/sq. in 2300 MBytes 1997: 3090 Mbit/sq. in 8100 MBytes source: New York Times, 2/23/98, page C 3, “Makers of disk drives crowd even mroe data into even smaller spaces” 1/17/01 CMPUT 429/CMPE 382 Amaral

1 inch disk drive! • 2000 IBM Micro. Drive: – 1. 7” x 1. 4” x 0. 2” – 1 GB, 3600 RPM, 5 MB/s, 15 ms seek – Digital camera, Palm. PC? • 2006 Micro. Drive? • 9 GB, 50 MB/s! – Assuming it finds a niche in a successful product – Assuming past trends continue 1/17/01 CMPUT 429/CMPE 382 Amaral

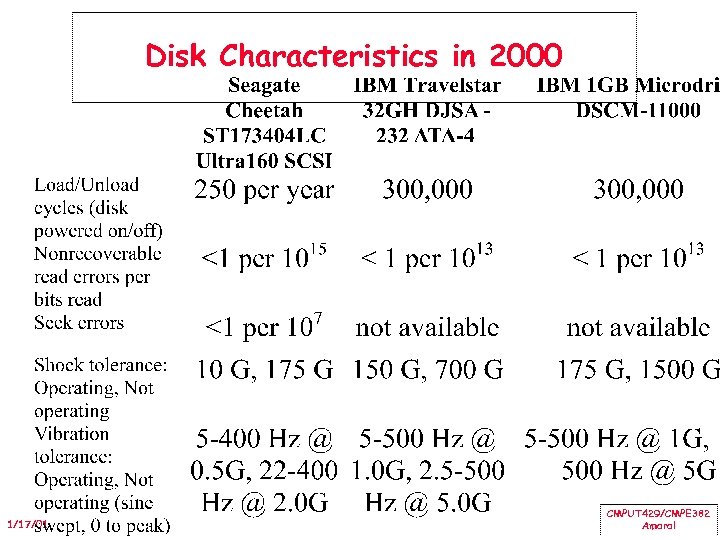
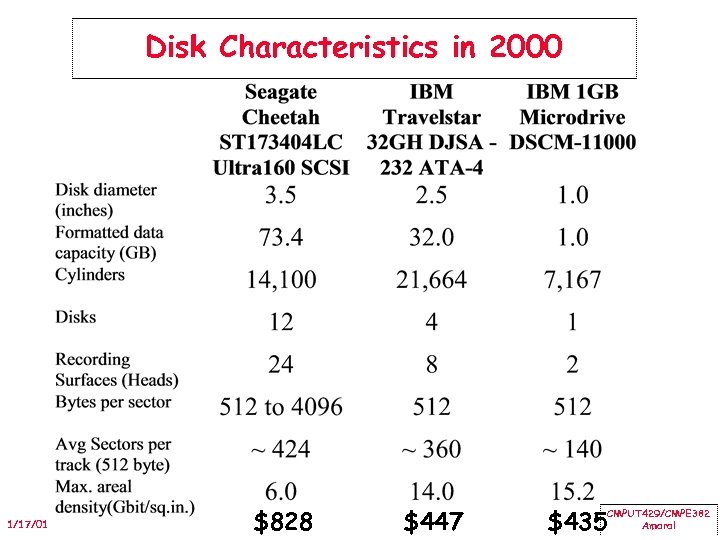Disk Characteristics in 2000 1/17/01 $828 $447 $435 CMPUT 429/CMPE 382 Amaral

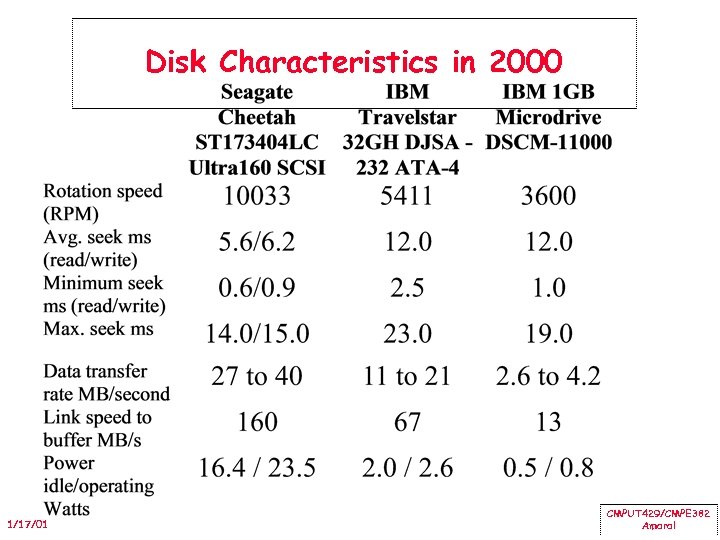Disk Characteristics in 2000 1/17/01 CMPUT 429/CMPE 382 Amaral

Disk Characteristics in 2000 1/17/01 CMPUT 429/CMPE 382 Amaral

Disk Characteristics in 2000 1/17/01 CMPUT 429/CMPE 382 Amaral

Fallacy: Use Data Sheet “Average Seek” Time • Manufacturers needed standard for fair comparison (“benchmark”) – Calculate all seeks from all tracks, divide by number of seeks => “average” • Real average would be based on how data laid out on disk, where seek in real applications, then measure performance – Usually, tend to seek to tracks nearby, not to random track • Rule of Thumb: observed average seek time is typically about 1/4 to 1/3 of quoted seek time (i. e. , 3 X-4 X faster) – Barracuda 180 X avg. seek: 7. 4 ms 2. 5 ms 1/17/01 CMPUT 429/CMPE 382 Amaral

Fallacy: Use Data Sheet Transfer Rate • Manufacturers quote the speed off the data rate off the surface of the disk • Sectors contain an error detection and correction field (can be 20% of sector size) plus sector number as well as data • There are gaps between sectors on track • Rule of Thumb: disks deliver about 3/4 of internal media rate (1. 3 X slower) for data • For example, Barracuda 180 X quotes 64 to 35 MB/sec internal media rate 47 to 26 MB/sec external data rate (74%) 1/17/01 CMPUT 429/CMPE 382 Amaral

Disk Performance Example • Calculate time to read 64 KB for Ultra. Star 72 again, this time using 1/3 quoted seek time, 3/4 of internal outer track bandwidth; (12. 7 ms before) Disk latency = average seek time + average rotational delay + transfer time + controller overhead = (0. 33 * 7. 4 ms) + 0. 5 * 1/(7200 RPM) + 64 KB / (0. 75 * 65 MB/s) + 0. 1 ms = 2. 5 ms + 0. 5 /(7200 RPM/(60000 ms/M)) + 64 KB / (47 KB/ms) + 0. 1 ms = 2. 5 + 4. 2 + 1. 4 + 0. 1 ms = 8. 2 ms (64% of 12. 7) 1/17/01 CMPUT 429/CMPE 382 Amaral

Future Disk Size and Performance • Continued advance in capacity (60%/yr) and bandwidth (40%/yr) • Slow improvement in seek, rotation (8%/yr) • Time to read whole disk Year Sequentially Randomly (1 sector/seek) 1990 4 minutes 6 hours 2000 12 minutes 1 week(!) • 3. 5” form factor make sense in 5 yrs? – What is capacity, bandwidth, seek time, RPM? – Assume today 80 GB, 30 MB/sec, 6 ms, 10000 RPM 1/17/01 CMPUT 429/CMPE 382 Amaral

Tape vs. Disk • Longitudinal tape uses same technology as hard disk; tracks its density improvements • Disk head flies above surface, tape head lies on surface • Disk fixed, tape removable • Inherent cost-performance based on geometries: fixed rotating platters with gaps (random access, limited area, 1 media / reader) vs. removable long strips wound on spool (sequential access, "unlimited" length, multiple / reader) • Helical Scan (VCR, Camcoder, DAT) Spins head at angle to tape to improve density 1/17/01 CMPUT 429/CMPE 382 Amaral

Current Drawbacks to Tape • Tape wear out: – Helical 100 s of passes to 1000 s for longitudinal • Head wear out: – 2000 hours for helical • Both must be accounted for in economic / reliability model • Bits stretch • Readers must be compatible with multiple generations of media • Long rewind, eject, load, spin-up times; not inherent, just no need in marketplace • Designed for archival 1/17/01 CMPUT 429/CMPE 382 Amaral

Automated Cartridge System: Storage. Tek Powderhorn 9310 7. 7 feet 8200 pounds, 1. 1 kilowatts 10. 7 feet • 6000 x 50 GB 9830 tapes = 300 TBytes in 2000 (uncompressed) – Library of Congress: all information in the world; in 1992, ASCII of all books = 30 TB – Exchange up to 450 tapes per hour (8 secs/tape) 1/17/01 • 1. 7 to 7. 7 Mbyte/sec per reader, up to 10 readers CMPUT 429/CMPE 382 Amaral

Library vs. Storage • Getting books today as quaint as programming in the 1970 s: – punch cards, batch processing – wander thru shelves, anticipatory purchasing • • • 1/17/01 Cost $1 per book to check out $30 for a catalogue entry 30% of all books never checked out Write only journals? Digital library can transform campuses CMPUT 429/CMPE 382 Amaral

Whither tape? • Investment in research: – 90% of disks shipped in PCs; 100% of PCs have disks – ~0% of tape readers shipped in PCs; ~0% of PCs have tapes • Before, N disks / tape; today, N tapes / disk – 40 GB/DLT tape (uncompressed) – 80 to 192 GB/3. 5" disk (uncompressed) • Cost per GB: – – – In past, 10 X to 100 X tape cartridge vs. disk Jan 2001: 40 GB for $53 (DLT cartridge), $2800 for reader $1. 33/GB cartridge, $2. 03/GB 100 cartridges + 1 reader ($10995 for 1 reader + 15 tape autoloader, $10. 50/GB) Jan 2001: 80 GB for $244 (IDE, 5400 RPM), $3. 05/GB Will $/GB tape v. disk cross in 2001? 2002? 2003? • Storage field is based on tape backup; what should CMPUT 429/CMPE 382 we do? Discussion if time permits? 1/17/01 Amaral

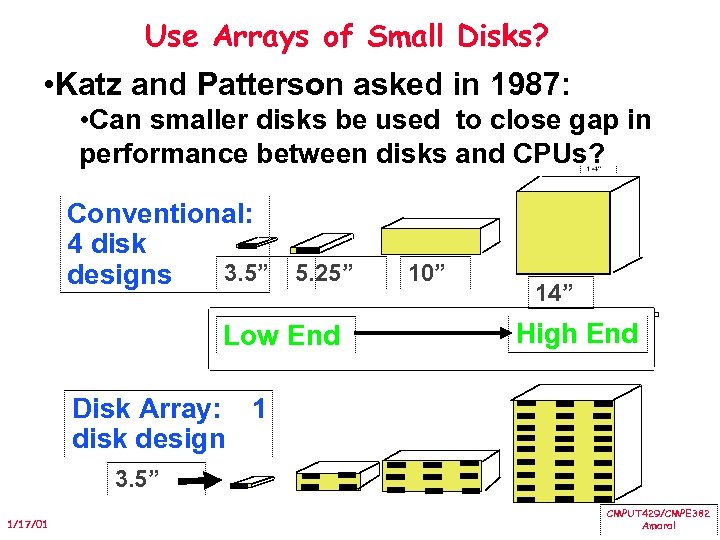Use Arrays of Small Disks? • Katz and Patterson asked in 1987: • Can smaller disks be used to close gap in performance between disks and CPUs? Conventional: 4 disk 3. 5” 5. 25” 10” designs Low End 14” High End Disk Array: 1 disk design 3. 5” 1/17/01 CMPUT 429/CMPE 382 Amaral

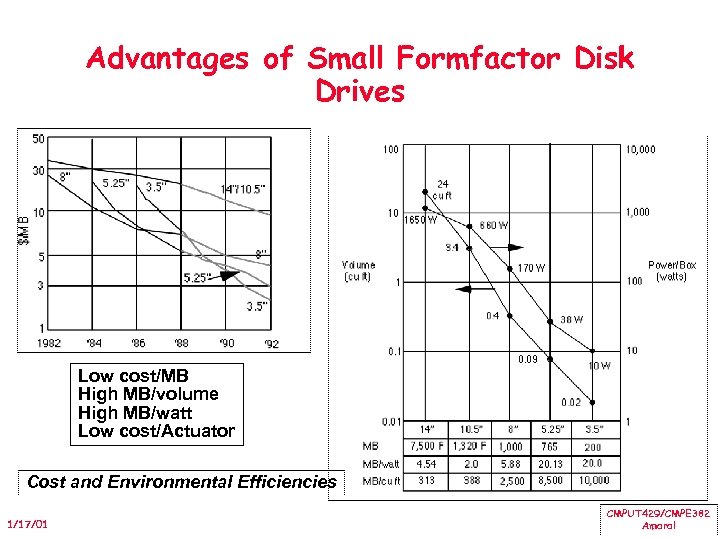Advantages of Small Formfactor Disk Drives Low cost/MB High MB/volume High MB/watt Low cost/Actuator Cost and Environmental Efficiencies 1/17/01 CMPUT 429/CMPE 382 Amaral

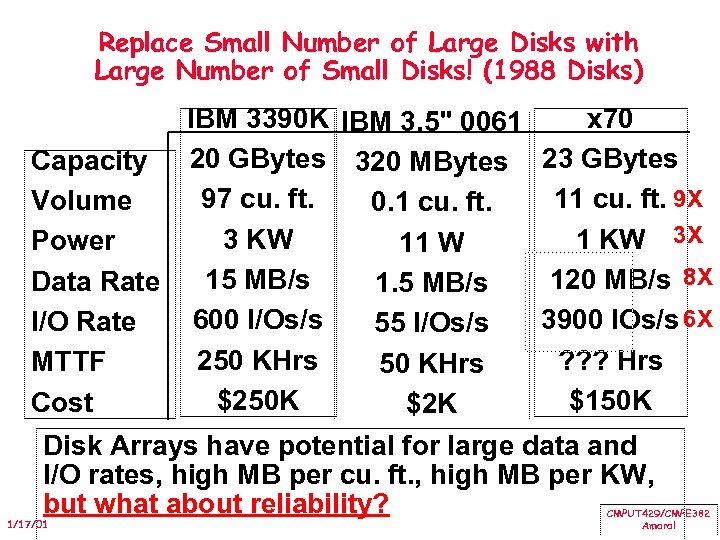Replace Small Number of Large Disks with Large Number of Small Disks! (1988 Disks) IBM 3390 K IBM 3. 5" 0061 x 70 Capacity 20 GBytes 320 MBytes 23 GBytes 97 cu. ft. 11 cu. ft. 9 X Volume 0. 1 cu. ft. 3 KW 1 KW 3 X Power 11 W 120 MB/s 8 X Data Rate 15 MB/s 1. 5 MB/s 3900 IOs/s 6 X I/O Rate 600 I/Os/s 55 I/Os/s 250 KHrs ? ? ? Hrs MTTF 50 KHrs $250 K $150 K Cost $2 K Disk Arrays have potential for large data and I/O rates, high MB per cu. ft. , high MB per KW, but what about reliability? 1/17/01 CMPUT 429/CMPE 382 Amaral

Array Reliability • Reliability of N disks = Reliability of 1 Disk ÷ N 50, 000 Hours ÷ 70 disks = 700 hours Disk system MTTF: Drops from 6 years to 1 month! • Arrays (without redundancy) too unreliable to be useful! Hot spares support reconstruction in parallel with access: very high media availability can be achieved 1/17/01 CMPUT 429/CMPE 382 Amaral

Redundant Arrays of (Inexpensive) Disks • Files are "striped" across multiple disks • Redundancy yields high data availability – Availability: service still provided to user, even if some components failed • Disks will still fail • Contents reconstructed from data stored in the array redundantly Capacity penalty to store redundant info Bandwidth penalty to update redundant info 1/17/01 CMPUT 429/CMPE 382 Amaral

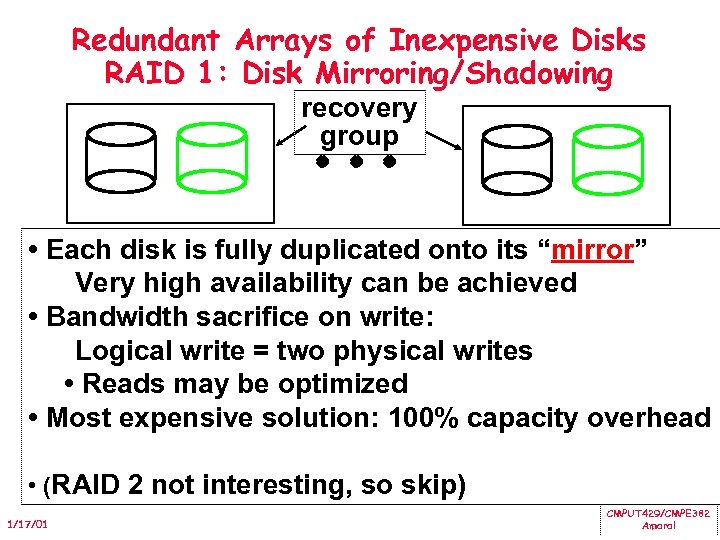Redundant Arrays of Inexpensive Disks RAID 1: Disk Mirroring/Shadowing recovery group • Each disk is fully duplicated onto its “mirror” Very high availability can be achieved • Bandwidth sacrifice on write: Logical write = two physical writes • Reads may be optimized • Most expensive solution: 100% capacity overhead • (RAID 2 not interesting, so skip) 1/17/01 CMPUT 429/CMPE 382 Amaral

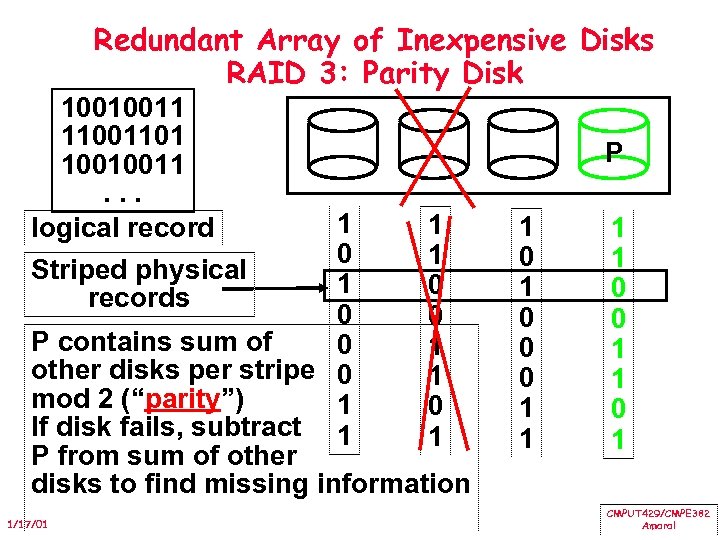Redundant Array of Inexpensive Disks RAID 3: Parity Disk 10010011 11001101 10010011. . . logical record 1 1 0 1 Striped physical 1 0 records 0 0 P contains sum of 0 1 other disks per stripe 0 1 mod 2 (“parity”) 1 0 If disk fails, subtract 1 1 P from sum of other disks to find missing information 1/17/01 P 1 0 0 0 1 1 0 1 CMPUT 429/CMPE 382 Amaral

RAID 3 • Sum computed across recovery group to protect against hard disk failures, stored in P disk • Logically, a single high capacity, high transfer rate disk: good for large transfers • Wider arrays reduce capacity costs, but decreases availability • 33% capacity cost for parity in this configuration 1/17/01 CMPUT 429/CMPE 382 Amaral

Inspiration for RAID 4 • RAID 3 relies on parity disk to discover errors on Read • But every sector has an error detection field • Rely on error detection field to catch errors on read, not on the parity disk • Allows independent reads to different disks simultaneously 1/17/01 CMPUT 429/CMPE 382 Amaral

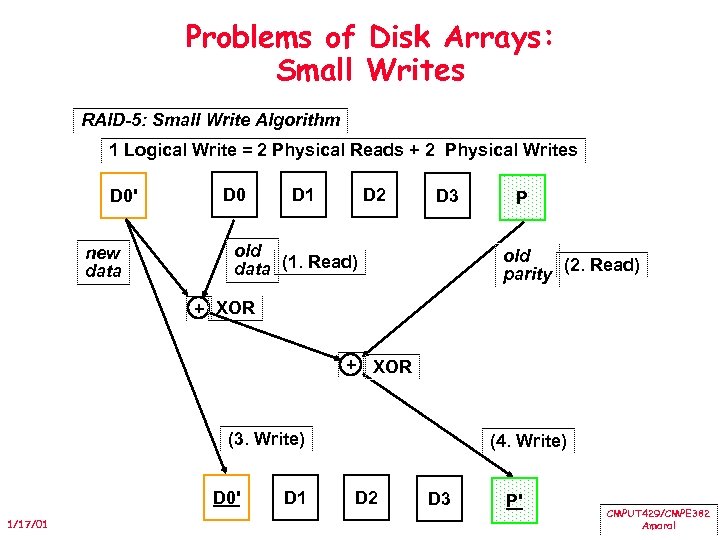Problems of Disk Arrays: Small Writes RAID-5: Small Write Algorithm 1 Logical Write = 2 Physical Reads + 2 Physical Writes D 0' new data D 0 D 1 D 2 D 3 old data (1. Read) P old (2. Read) parity + XOR (3. Write) D 0' 1/17/01 D 1 (4. Write) D 2 D 3 P' CMPUT 429/CMPE 382 Amaral

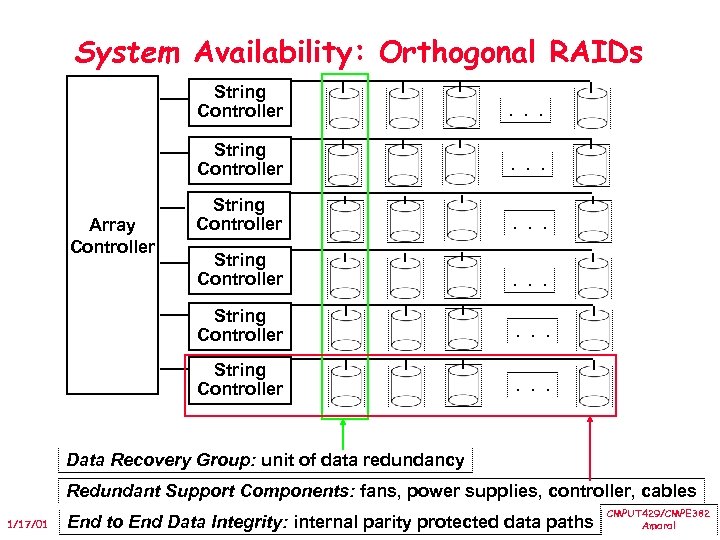System Availability: Orthogonal RAIDs String Controller . . . String Controller Array Controller . . . Data Recovery Group: unit of data redundancy Redundant Support Components: fans, power supplies, controller, cables 1/17/01 End to End Data Integrity: internal parity protected data paths CMPUT 429/CMPE 382 Amaral

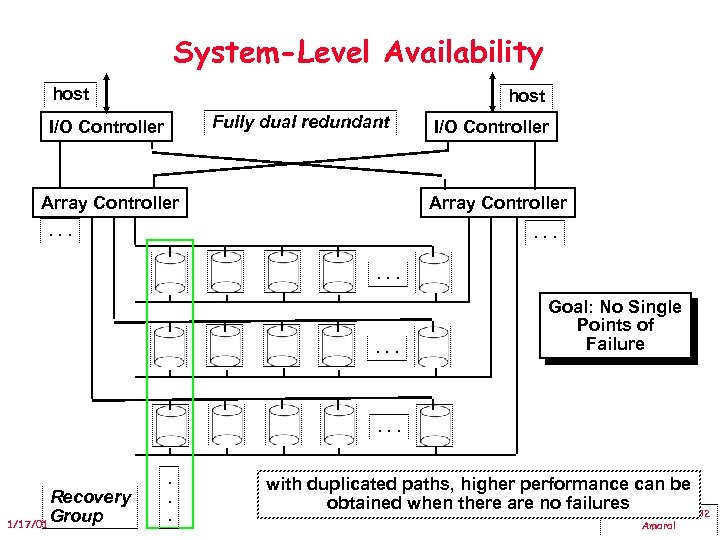System-Level Availability host Fully dual redundant I/O Controller Array Controller . . . Goal: No Single Points of Failure . . . Recovery Group 1/17/01 . . . with duplicated paths, higher performance can be obtained when there are no failures CMPUT 429/CMPE 382 Amaral

Berkeley History: RAID -I • RAID-I (1989) – Consisted of a Sun 4/280 workstation with 128 MB of DRAM, four dual-string SCSI controllers, 28 5. 25 -inch SCSI disks and specialized disk striping software • Today RAID is $19 billion dollar industry, 80% non. PC disks sold in RAIDs 1/17/01 CMPUT 429/CMPE 382 Amaral

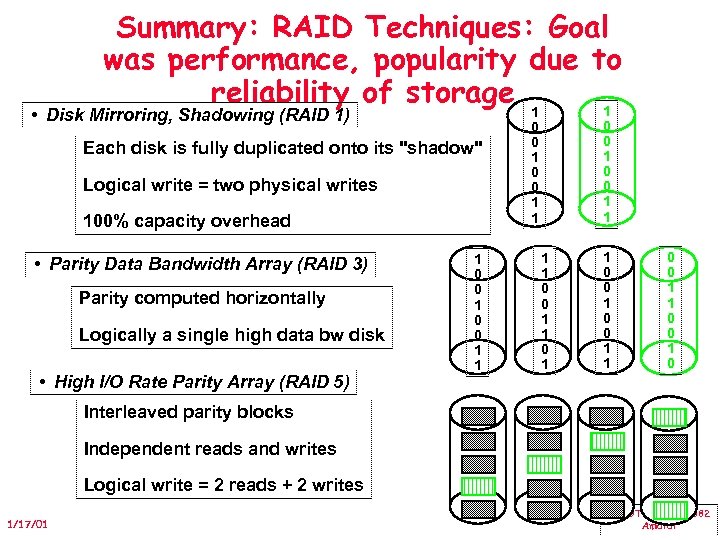Summary: RAID Techniques: Goal was performance, popularity due to reliability of storage 1 1 • Disk Mirroring, Shadowing (RAID 1) Each disk is fully duplicated onto its "shadow" Logical write = two physical writes 100% capacity overhead • Parity Data Bandwidth Array (RAID 3) Parity computed horizontally Logically a single high data bw disk • High I/O Rate Parity Array (RAID 5) 1 0 0 1 1 0 0 1 1 0 0 1 0 Interleaved parity blocks Independent reads and writes Logical write = 2 reads + 2 writes 1/17/01 CMPUT 429/CMPE 382 Amaral

Summary Storage • Disks: – Extraodinary advance in capacity/drive, $/GB – Currently 17 Gbit/sq. in. ; can continue past 100 Gbit/sq. in. ? – Bandwidth, seek time not keeping up: 3. 5 inch form factor makes sense? 2. 5 inch form factor in near future? 1. 0 inch form factor in long term? • Tapes – No investment, must be backwards compatible – Are they already dead? – What is a tapeless backup system? 1/17/01 CMPUT 429/CMPE 382 Amaral

Reliability Definitions • Examples on why precise definitions so important for reliability • Is a programming mistake a fault, error, or failure? – Are we talking about the time it was designed or the time the program is run? – If the running program doesn’t exercise the mistake, is it still a fault/error/failure? • If an alpha particle hits a DRAM memory cell, is it a fault/error/failure if it doesn’t change the value? – Is it a fault/error/failure if the memory doesn’t access the changed bit? – Did a fault/error/failure still occur if the memory had error correction and delivered the corrected value to the CPU? 1/17/01 CMPUT 429/CMPE 382 Amaral

IFIP Standard terminology • Computer system dependability: quality of delivered service such that reliance can be placed on service • Service is observed actual behavior as perceived by other system(s) interacting with this system’s users • Each module has ideal specified behavior, where service specification is agreed description of expected behavior • A system failure occurs when the actual behavior deviates from the specified behavior • failure occurred because an error, a defect in module • The cause of an error is a fault • When a fault occurs it creates a latent error, which becomes effective when it is activated • When error actually affects the delivered service, a failure occurs (time from error to failure is error CMPUT 429/CMPE 382 1/17/01 latency) Amaral

Fault v. (Latent) Error v. Failure • A fault creates one or more latent errors • Properties of errors are – a latent error becomes effective once activated – an error may cycle between its latent and effective states – an effective error often propagates from one component to another, thereby creating new errors • Effective error is either a formerly-latent error in that component or it propagated from another error • A component failure occurs when the error affects the delivered service • These properties are recursive, and apply to any component in the system • An error is manifestation in the system of a fault, a failure is manifestation on the service of an error 1/17/01 CMPUT 429/CMPE 382 Amaral

Fault v. (Latent) Error v. Failure • An error is manifestation in the system of a fault, a failure is manifestation on the service of an error • Is a programming mistake a fault, error, or failure? – Are we talking about the time it was designed or the time the program is run? – If the running program doesn’t exercise the mistake, is it still a fault/error/failure? • A programming mistake is a fault • the consequence is an error (or latent error) in the software • upon activation, the error becomes effective • when this effective error produces erroneous data which affect the delivered service, a failure occurs 1/17/01 CMPUT 429/CMPE 382 Amaral

Fault v. (Latent) Error v. Failure • An error is manifestation in the system of a fault, a failure is manifestation on the service of an error • Is If an alpha particle hits a DRAM memory cell, is it a fault/error/failure if it doesn’t change the value? – Is it a fault/error/failure if the memory doesn’t access the changed bit? – Did a fault/error/failure still occur if the memory had error correction and delivered the corrected value to the CPU? 1/17/01 • An alpha particle hitting a DRAM can be a fault • if it changes the memory, it creates an error • error remains latent until effected memory word is read • if the effected word error affects the delivered service, a failure occurs CMPUT 429/CMPE 382 Amaral

Fault v. (Latent) Error v. Failure • An error is manifestation in the system of a fault, a failure is manifestation on the service of an error • What if a person makes a mistake, data is altered, and service is affected? • fault: • error: • latent: • failure: 1/17/01 CMPUT 429/CMPE 382 Amaral

Fault Tolerance vs Disaster Tolerance • Fault-Tolerance (or more properly, Error. Tolerance): mask local faults (prevent errors from becoming failures) – RAID disks – Uninterruptible Power Supplies – Cluster Failover • Disaster Tolerance: masks site errors (prevent site errors from causing service failures) – Protects against fire, flood, sabotage, . . – Redundant system and service at remote site. – Use design diversity From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

Defining reliability and availability quantitatively • Users perceive a system alternating between 2 states of service with respect to service specification: 1. service accomplishment, where service is delivered as specified, 2. service interruption, where the delivered service is different from the specified service, measured as Mean Time To Repair (MTTR) Transitions between these 2 states are caused by failures (from state 1 to state 2) or restorations (2 to 1) • module reliability: a measure of continuous service accomplishment (or of time to failure) from a reference point, e. g, Mean Time To Failure (MTTF) – The reciprocal of MTTF is failure rate 1/17/01 • module availability: measure of service accomplishment with respect to alternation between the 2 states of accomplishment and interruption = MTTF / (MTTF+MTTR) CMPUT 429/CMPE 382 Amaral

Fail-Fast is Good, Repair is Needed Lifecycle of a module fail fast gives short fault latency High Availability is low UN Availability Unavailability MTTR MTTF+MTTR As MTTF>>MTTR, improving either MTTR or MTTF gives benefit Note: Mean Time Between Failures (MTBF)= MTTF+MTTR From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

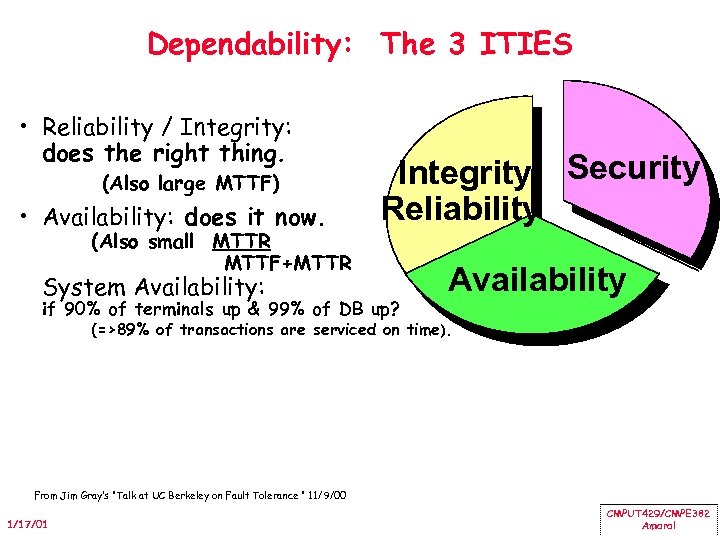Dependability: The 3 ITIES • Reliability / Integrity: does the right thing. (Also large MTTF) • Availability: does it now. (Also small MTTR MTTF+MTTR System Availability: Integrity Security Reliability if 90% of terminals up & 99% of DB up? Availability (=>89% of transactions are serviced on time). From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

Reliability Example • If assume collection of modules have exponentially distributed lifetimes (age of compoent doesn't matter in failure probability) and modules fail independently, overall failure rate of collection is sum of failure rates of modules • Calculate MTTF of a disk subsystem with – 10 disks, each rated at 1, 000 hour MTTF – – 1 1 SCSI controller, 500, 000 hour MTTF power supply, 200, 000 hour MTTF fan, 200, 000 MTTF SCSI cable, 1, 000 hour MTTF • Failure Rate = 10*1/1, 000 + 1/500, 000 + 1/200, 000 + 1/1, 000 = (10 +2 +5 +5 +1)/1, 000 = 23/1, 000 • MTTF=1/Failure Rate = 1, 000/23 = 43, 500 hrs CMPUT 429/CMPE 382 1/17/01 Amaral

What's wrong with MTTF? • 1, 000 MTTF > 100 years; ~ infinity? • How calculated? – Put, say, 2000 in a room, calculate failures in 60 days, and then calculate the rate – As long as <=3 failures => 1, 000 hr MTTF • • • Suppose we did this with people? 1998 deaths per year in US ("Failure Rate") Deaths 5 to 14 year olds = 20/100, 000 MTTFhuman = 100, 000/20 = 5, 000 years Deaths >85 year olds = 20, 000/100, 000 MTTFhuman = 100, 000/20, 000 = 5 years source: "Deaths: Final Data for 1998, " www. cdc. gov/nchs/data/nvs 48_11. pdf 1/17/01 CMPUT 429/CMPE 382 Amaral

What's wrong with MTTF? 1/17/01 • 1, 000 MTTF > 100 years; ~ infinity? • But disk lifetime is 5 years! • => if you replace a disk every 5 years, on average it wouldn't fail until 21 st replacement • A better unit: % that fail • Fail over lifetime if had 1000 disks for 5 years = (1000 disks * 365*24) / 1, 000 hrs/failure = 43, 800, 000 / 1, 000 = 44 failures = 4. 4% fail with 1, 000 MTTF • Detailed disk spec lists failures/million/month • Typically about 800 failures per month per million disks at 1, 000 MTTF, or about 1% per year for 5 year disk lifetime CMPUT 429/CMPE 382 Amaral

Dependability Big Idea: No Single Point of Failure • Since Hardware MTTF is often 100, 000 to 1, 000 hours and MTTF is often 1 to 10 hours, there is a good chance that if one component fails it will be repaired before a second component fails • Hence design systems with sufficient redundancy that there is No Single Point of Failure 1/17/01 CMPUT 429/CMPE 382 Amaral

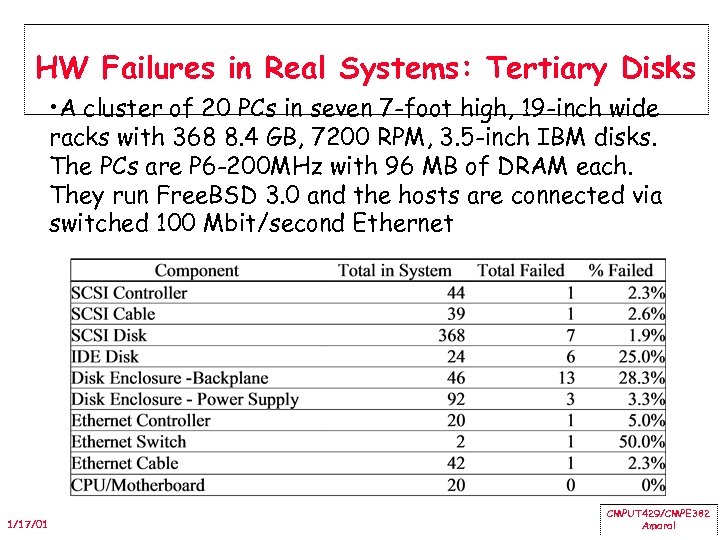HW Failures in Real Systems: Tertiary Disks • A cluster of 20 PCs in seven 7 -foot high, 19 -inch wide racks with 368 8. 4 GB, 7200 RPM, 3. 5 -inch IBM disks. The PCs are P 6 -200 MHz with 96 MB of DRAM each. They run Free. BSD 3. 0 and the hosts are connected via switched 100 Mbit/second Ethernet 1/17/01 CMPUT 429/CMPE 382 Amaral

When To Repair? Chances Of Tolerating A Fault are 1000: 1 (class 3) A 1995 study: Processor & Disc Rated At ~ 10 khr MTTF Computed Single Observed Failures Double Fails Ratio 10 k Processor Fails 14 Double ~ 1000 : 1 40 k Disc Fails, 26 Double ~ 1000 : 1 Hardware Maintenance: On-Line Maintenance "Works" 999 Times Out Of 1000. The chance a duplexed disc will fail during maintenance? 1: 1000 Risk Is 30 x Higher During Maintenance => Do It Off Peak Hour Software Maintenance: Repair Only Virulent Bugs Wait For Next Release To Fix Benign Bugs From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

Sources of Failures MTTF Power Failure: Phone Lines Soft Hardware Modules: Software: MTTR 2000 hr >. 1 hr 4000 hr 100, 000 hr 10 hr (many are transient) 1 Bug/1000 Lines Of Code (after vendor-user testing) => Thousands of bugs in System! Most software failures are transient: dump & restart system. Useful fact: 8, 760 hrs/year ~ 10 k hr/year From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

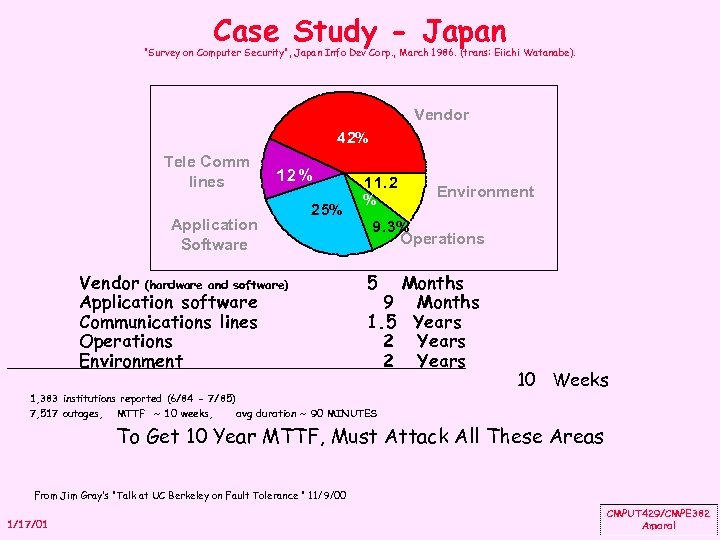Case Study - Japan "Survey on Computer Security", Japan Info Dev Corp. , March 1986. (trans: Eiichi Watanabe). Vendor 4 2% Tele Comm lines 12 % Application Software 2 5% Vendor (hardware and software) Application software Communications lines Operations Environment 1 1. 2 % Environment 9. 3% Operations 5 Months 9 Months 1. 5 Years 2 Years 1, 383 institutions reported (6/84 - 7/85) 7, 517 outages, MTTF ~ 10 weeks, avg duration ~ 90 MINUTES 10 Weeks To Get 10 Year MTTF, Must Attack All These Areas From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

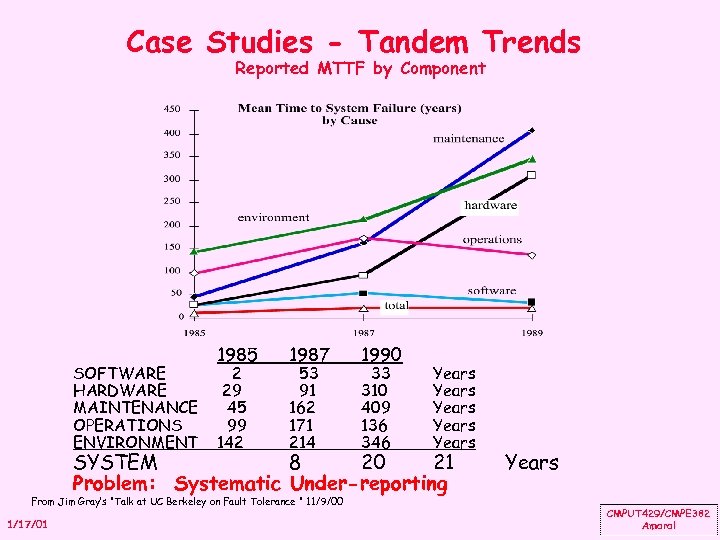Case Studies - Tandem Trends Reported MTTF by Component SOFTWARE HARDWARE MAINTENANCE OPERATIONS ENVIRONMENT 1985 2 29 45 99 142 1987 53 91 162 171 214 1990 33 310 409 136 346 Years Years SYSTEM 8 20 21 Problem: Systematic Under-reporting From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 Years CMPUT 429/CMPE 382 Amaral

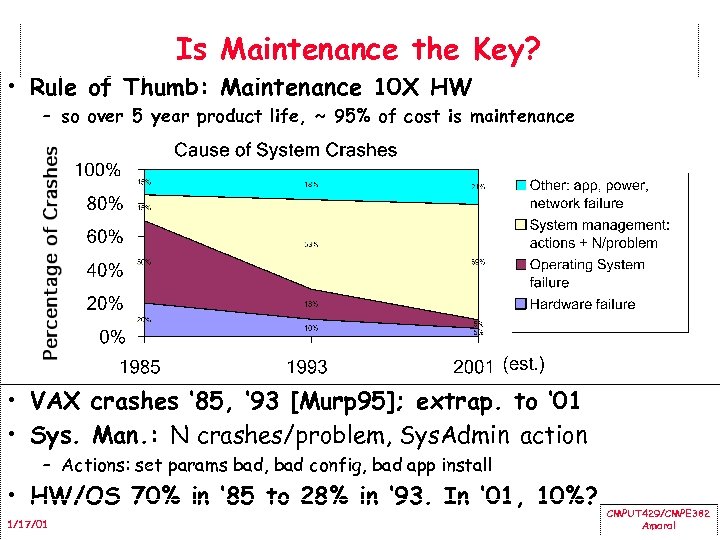Is Maintenance the Key? • Rule of Thumb: Maintenance 10 X HW – so over 5 year product life, ~ 95% of cost is maintenance • VAX crashes ‘ 85, ‘ 93 [Murp 95]; extrap. to ‘ 01 • Sys. Man. : N crashes/problem, Sys. Admin action – Actions: set params bad, bad config, bad app install • HW/OS 70% in ‘ 85 to 28% in ‘ 93. In ‘ 01, 10%? 1/17/01 CMPUT 429/CMPE 382 Amaral

OK: So Far Hardware fail-fast is easy Redundancy plus Repair is great (Class 7 availability) Hardware redundancy & repair is via modules. How can we get instant software repair? We Know How To Get Reliable Storage RAID Or Dumps And Transaction Logs. We Know How To Get Available Storage Fail Soft Duplexed Discs (RAID 1. . . N). ? How do we get reliable execution? ? How do we get available execution? From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

Does Hardware Fail Fast? 4 of 384 Disks that failed in Tertiary Disk 1/17/01 CMPUT 429/CMPE 382 Amaral

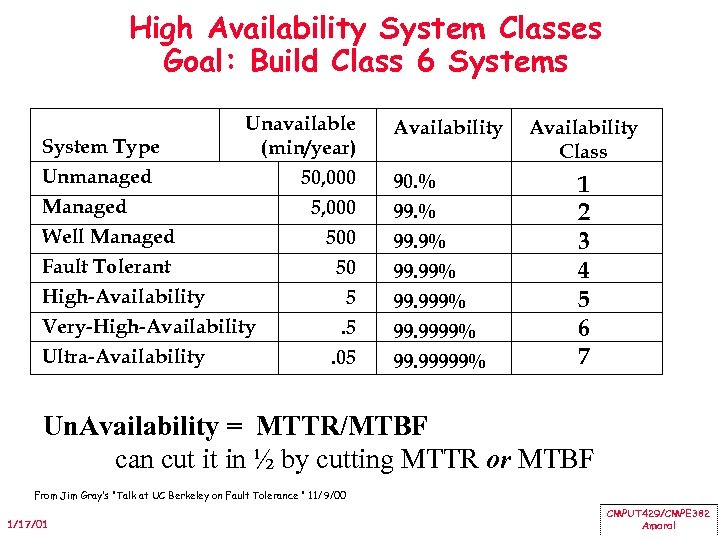High Availability System Classes Goal: Build Class 6 Systems Unavailable System Type (min/year) Unmanaged 50, 000 Managed 5, 000 Well Managed 500 Fault Tolerant 50 High-Availability 5 Very-High-Availability. 5 Ultra-Availability. 05 Availability 90. % 99. 9% 99. 999% 99. 99999% Availability Class 1 2 3 4 5 6 7 Un. Availability = MTTR/MTBF can cut it in ½ by cutting MTTR or MTBF From Jim Gray’s “Talk at UC Berkeley on Fault Tolerance " 11/9/00 1/17/01 CMPUT 429/CMPE 382 Amaral

How Realistic is "5 Nines"? • HP claims HP-9000 server HW and HP-UX OS can deliver 99. 999% availability guarantee “in certain pre-defined, pre-tested customer environments” – Application faults? – Operator faults? – Environmental faults? • Collocation sites (lots of computers in 1 building on Internet) have – 1 network outage per year (~1 day) – 1 power failure per year (~1 day) • Microsoft Network unavailable recently for a day due to problem in Domain Name Server: if only outage per year, 99. 7% or 2 Nines 1/17/01 CMPUT 429/CMPE 382 Amaral

Summary: Dependability • Fault => Latent errors in system => Failure in service • Reliability: quantitative measure of time to failure (MTTF) – Assuming expoentially distributed independent failures, can calculate MTTF system from MTTF of components • Availability: quantitative measure % of time delivering desired service • Can improve Availability via greater MTTF or smaller MTTR (such as using standby spares) • No single point of failure a good hardware guideline, as everything can fail • Components often fail slowly • Real systems: problems in maintenance, operation as well as hardware, software 1/17/01 CMPUT 429/CMPE 382 Amaral

Summary: Dependability • Fault => Latent errors in system => Failure in service • Reliability: quantitative measure of time to failure (MTTF) – Assuming expoentially distributed independent failures, can calculate MTTF system from MTTF of components • Availability: quantitative measure % of time delivering desired service • Can improve Availability via greater MTTF or smaller MTTR (such as using standby spares) • No single point of failure a good hardware guideline, as everything can fail • Components often fail slowly • Real systems: problems in maintenance, operation as well as hardware, software 1/17/01 CMPUT 429/CMPE 382 Amaral

Introduction to Queueing Theory Arrivals Departures • More interested in long term, steady state than in startup => Arrivals = Departures • Little’s Law: Mean number tasks in system = arrival rate x mean reponse time – Observed by many, Little was first to prove 1/17/01 • Applies to any system in equilibrium, as long as nothing in black box is creating or destroying tasks CMPUT 429/CMPE 382 Amaral

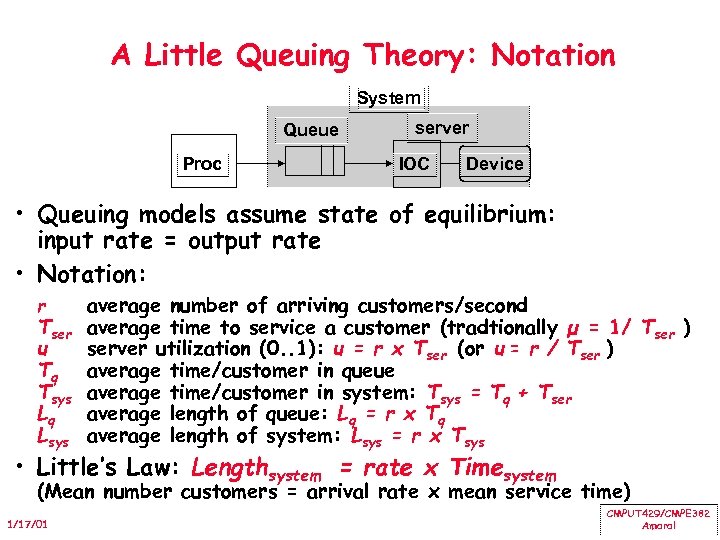A Little Queuing Theory: Notation System Queue Proc server IOC Device • Queuing models assume state of equilibrium: input rate = output rate • Notation: r Tser u Tq Tsys Lq Lsys average number of arriving customers/second average time to service a customer (tradtionally µ = 1/ Tser ) server utilization (0. . 1): u = r x Tser (or u = r / Tser ) average time/customer in queue average time/customer in system: Tsys = Tq + Tser average length of queue: Lq = r x Tq average length of system: Lsys = r x Tsys • Little’s Law: Lengthsystem = rate x Timesystem (Mean number customers = arrival rate x mean service time) 1/17/01 CMPUT 429/CMPE 382 Amaral

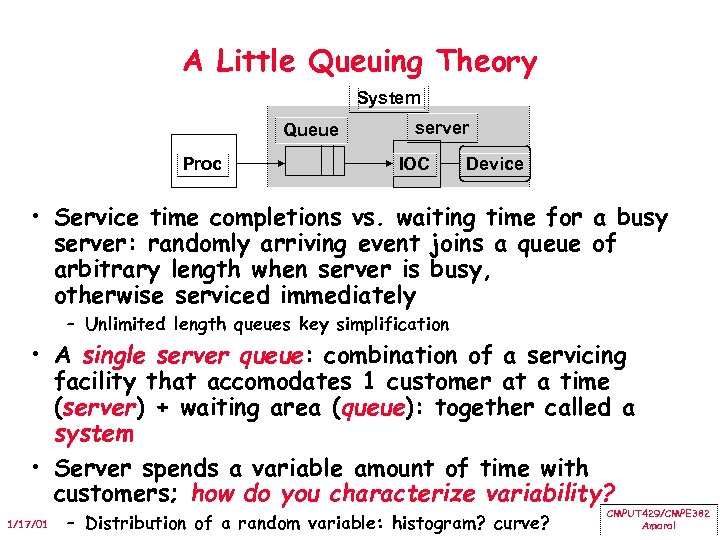A Little Queuing Theory System Queue Proc server IOC Device • Service time completions vs. waiting time for a busy server: randomly arriving event joins a queue of arbitrary length when server is busy, otherwise serviced immediately – Unlimited length queues key simplification • A single server queue: combination of a servicing facility that accomodates 1 customer at a time (server) + waiting area (queue): together called a system • Server spends a variable amount of time with customers; how do you characterize variability? 1/17/01 – Distribution of a random variable: histogram? curve? CMPUT 429/CMPE 382 Amaral

A Little Queuing Theory System Queue Proc server IOC Device • Server spends a variable amount of time with customers – Weighted mean m 1 = (f 1 x T 1 + f 2 x T 2 +. . . + fn x Tn)/F (F=f 1 + f 2. . . ) – variance = (f 1 x T 12 + f 2 x T 22 +. . . + fn x Tn 2)/F – m 12 Avg. » Must keep track of unit of measure (100 ms 2 vs. 0. 1 s 2 ) – Squared coefficient of variance: C = variance/m 12 » Unitless measure (100 ms 2 vs. 0. 1 s 2) • Exponential distribution C = 1 : most short relative to average, few others long; 90% < 2. 3 x average, 63% < average • Hypoexponential distribution C < 1 : most close to average, C=0. 5 => 90% < 2. 0 x average, only 57% < average • Hyperexponential distribution C > 1 : further from average 1/17/01 C=2. 0 => 90% < 2. 8 x average, 69% < average CMPUT 429/CMPE 382 Amaral

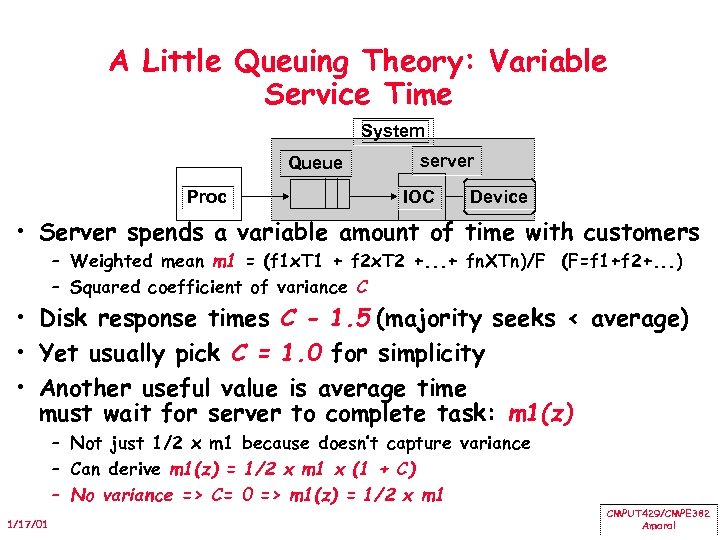A Little Queuing Theory: Variable Service Time System Queue Proc server IOC Device • Server spends a variable amount of time with customers – Weighted mean m 1 = (f 1 x. T 1 + f 2 x. T 2 +. . . + fn. XTn)/F (F=f 1+f 2+. . . ) – Squared coefficient of variance C • Disk response times C 1. 5 (majority seeks < average) • Yet usually pick C = 1. 0 for simplicity • Another useful value is average time must wait for server to complete task: m 1(z) – Not just 1/2 x m 1 because doesn’t capture variance – Can derive m 1(z) = 1/2 x m 1 x (1 + C) – No variance => C= 0 => m 1(z) = 1/2 x m 1 1/17/01 CMPUT 429/CMPE 382 Amaral

A Little Queuing Theory: Average Wait Time • Calculating average wait time in queue Tq – If something at server, it takes to complete on average m 1(z) – Chance server is busy = u; average delay is u x m 1(z) – All customers in line must complete; each avg Tser Tq = u x m 1(z) + Lq x Ts er= 1/2 x u x Tser x (1 + C) + Lq x Ts er Tq = 1/2 x u Tq x (1 – u) Tq = Ts er x x Ts er x (1 + C) + r x Tq x Ts er x (1 + C) + u x Tq = Ts er x u x (1 + C) /2 u x (1 + C) / (2 x (1 – u)) • Notation: r Tser u Tq Lq 1/17/01 average number of arriving customers/second average time to service a customer server utilization (0. . 1): u = r x Tser average time/customer in queue average length of queue: Lq= r x Tq CMPUT 429/CMPE 382 Amaral

A Little Queuing Theory: M/G/1 and M/M/1 • Assumptions so far: – – – System in equilibrium Time between two successive arrivals in line are random Server can start on next customer immediately after prior finishes No limit to the queue: works First-In-First-Out Afterward, all customers in line must complete; each avg Tser • Described “memoryless” or Markovian request arrival (M for C=1 exponentially random), General service distribution (no restrictions), 1 server: M/G/1 queue • When Service times have C = 1, M/M/1 queue Tq = Tser x u x (1 + C) /(2 x (1 – u)) = Tser x u / (1 – u) Tser u Tq 1/17/01 average time to service a customer server utilization (0. . 1): u = r x Tser average time/customer in queue CMPUT 429/CMPE 382 Amaral

A Little Queuing Theory: An Example • processor sends 10 x 8 KB disk I/Os per second, requests & service exponentially distrib. , avg. disk service = 20 ms • On average, how utilized is the disk? – What is the number of requests in the queue? – What is the average time spent in the queue? – What is the average response time for a disk request? • Notation: r Tser u Tq Tsys Lq Lsys 1/17/01 average number of arriving customers/second = 10 average time to service a customer = 20 ms (0. 02 s) server utilization (0. . 1): u = r x Tser= 10/s x. 02 s = 0. 2 average time/customer in queue = Tser x u / (1 – u) = 20 x 0. 2/(1 -0. 2) = 20 x 0. 25 = 5 ms (0. 005 s) average time/customer in system: Tsys =Tq +Tser= 25 ms average length of queue: Lq= r x Tq = 10/s x. 005 s = 0. 05 requests in queue average # tasks in system: Lsys = r x Tsys = 10/s x. 025 s CMPUT 429/CMPE 382 = 0. 25 Amaral

A Little Queuing Theory: Another Example • processor sends 20 x 8 KB disk I/Os per sec, requests & service exponentially distrib. , avg. disk service = 12 ms • On average, how utilized is the disk? – What is the number of requests in the queue? – What is the average time a spent in the queue? – What is the average response time for a disk request? • Notation: r Tser u Tq Tsys Lq 1/17/01 Lsys average number of arriving customers/second= 20 average time to service a customer= 12 ms server utilization (0. . 1): u = r x Tser= /s x. s = average time/customer in queue = Ts er x u / (1 – u) = x /( ) = x = average time/customer in system: Tsys =Tq +Tser= 16 ms average length of queue: Lq= r x Tq = /s x s = requests in queue average # tasks in system : Lsys = r x Tsys = /s x ms s = CMPUT 429/CMPE 382 Amaral

A Little Queuing Theory: Another Example • processor sends 20 x 8 KB disk I/Os per sec, requests & service exponentially distrib. , avg. disk service = 12 ms • On average, how utilized is the disk? – What is the number of requests in the queue? – What is the average time a spent in the queue? – What is the average response time for a disk request? • Notation: r Tser u Tq Tsys Lq 1/17/01 Lsys average number of arriving customers/second= 20 average time to service a customer= 12 ms server utilization (0. . 1): u = r x Tser= 20/s x. 012 s = 0. 24 average time/customer in queue = Ts er x u / (1 – u) = 12 x 0. 24/(1 -0. 24) = 12 x 0. 32 = 3. 8 ms average time/customer in system: Tsys =Tq +Tser= 15. 8 ms average length of queue: Lq= r x Tq = 20/s x. 0038 s = 0. 076 requests in queue average # tasks in system : Lsys = r x Tsys = 20/s x. 016 s = 0. 32 CMPUT 429/CMPE 382 Amaral

A Little Queuing Theory: Yet Another Example • Suppose processor sends 10 x 8 KB disk I/Os per second, squared coef. var. (C) = 1. 5, avg. disk service time = 20 ms • On average, how utilized is the disk? – What is the number of requests in the queue? – What is the average time a spent in the queue? – What is the average response time for a disk request? • Notation: r Tser u Tq Tsys Lq 1/17/01 average number of arriving customers/second= 10 average time to service a customer= 20 ms server utilization (0. . 1): u = r x Tser= 10/s x. 02 s = 0. 2 average time/customer in queue = Tser x u x (1 + C) /(2 x (1 – u)) = 20 x 0. 2(2. 5)/2(1 – 0. 2) = 20 x 0. 32 = 6. 25 ms average time/customer in system: Tsys = Tq +Tser= 26 ms average length of queue: Lq= r x Tq CMPUT 429/CMPE 382 = 10/s x. 006 s = 0. 06 requests in queue Amaral

Pitfall of Not using Queuing Theory • 1 st 32 -bit minicomputer (VAX-11/780) • How big should write buffer be? – Stores 10% of instructions, 1 MIPS • Buffer = 1 • => Avg. Queue Length = 1 vs. low response time 1/17/01 CMPUT 429/CMPE 382 Amaral