Clusters Recognition from Large Small World Graph Igor

Clusters Recognition from Large Small World Graph Igor Kanovsky, Lilach Prego Emek Yezreel College, Israel igork@yvc. ac. il University of Haifa, Israel gprego@netvision. net. il © Igor Kanovsky, Lilach Prego @ Graph 2004, Haifa, May 2004 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Small World Definition(1) Def. 1. The characteristic path length L(G) of a graph G = (V; E) is the average length of the shortest path between two vertices in G The clustering coefficient C(G)= of a graph G = (V; E) is the average clustering coefficient of its vertices C(v); Def. 2. 2 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Small World Definition(2) Def. 3. Clustering coefficient for vertex v: Where k(v) number of edges indicate v (degree of v) , N(v) – neighborhood of v. The clustering coefcient C(v) of a vertex v is the density of the subgraph induced by G[N(v)]. 3 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Small World Definition(3) Def. 4. Small World graph is a graph G(V, E) with L~LR and C>>CR where GR(VR, ER) - a random graph with |VR|=|V|, |ER|=|E|. A lot of real world graphs are Small World graphs: 1. Social relationships. 2. Business (organization) collaborations. 3. The Web. The Internet. 4. Biological data (DNA structure, cells metabolism etc. ). 4 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

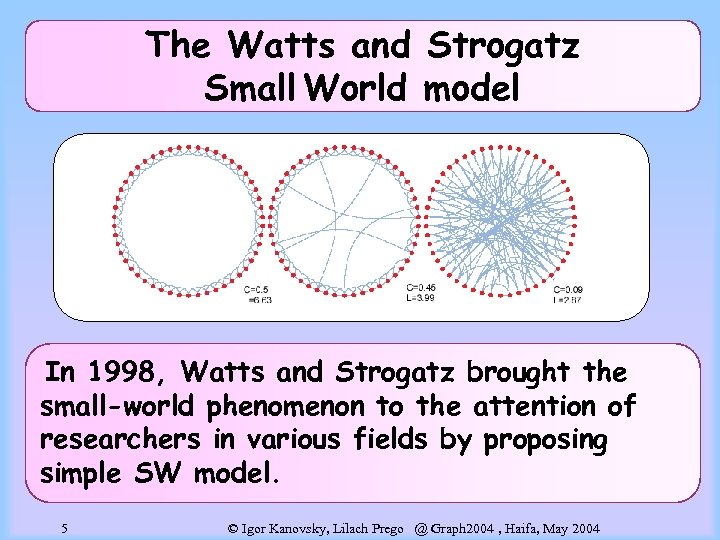The Watts and Strogatz Small World model In 1998, Watts and Strogatz brought the small-world phenomenon to the attention of researchers in various fields by proposing simple SW model. 5 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

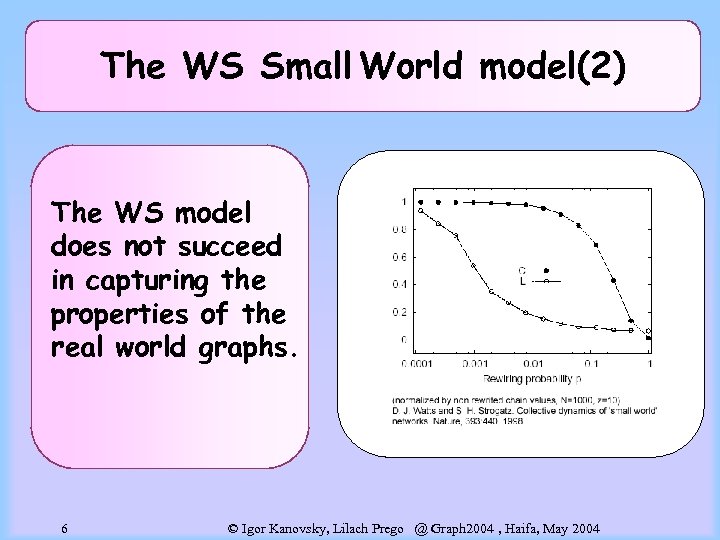The WS Small World model(2) The WS model does not succeed in capturing the properties of the real world graphs. 6 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

The Web as a graph The known significant properties of the Web as a graph are: 1. Small world topology. 2. Power-law distributions. 3. Bipartite cliques. 4. “Bow-tie" shape. A huge digraph with similar to the Web graph statistical characteristics is called a Web-like graph. 7 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

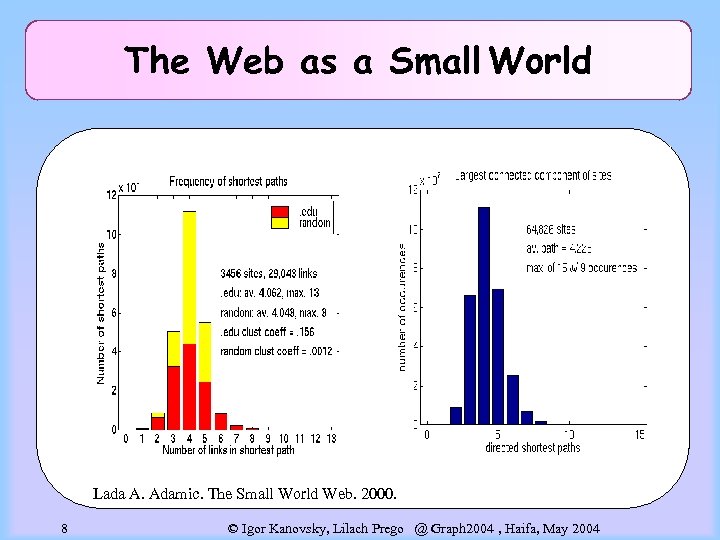The Web as a Small World Lada A. Adamic. The Small World Web. 2000. 8 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

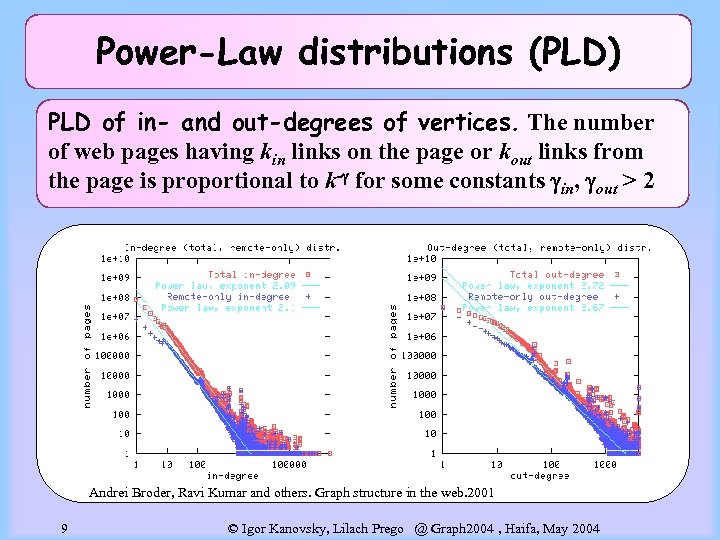Power-Law distributions (PLD) PLD of in- and out-degrees of vertices. The number of web pages having kin links on the page or kout links from the page is proportional to k- for some constants in, out > 2 Andrei Broder, Ravi Kumar and others. Graph structure in the web. 2001 9 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

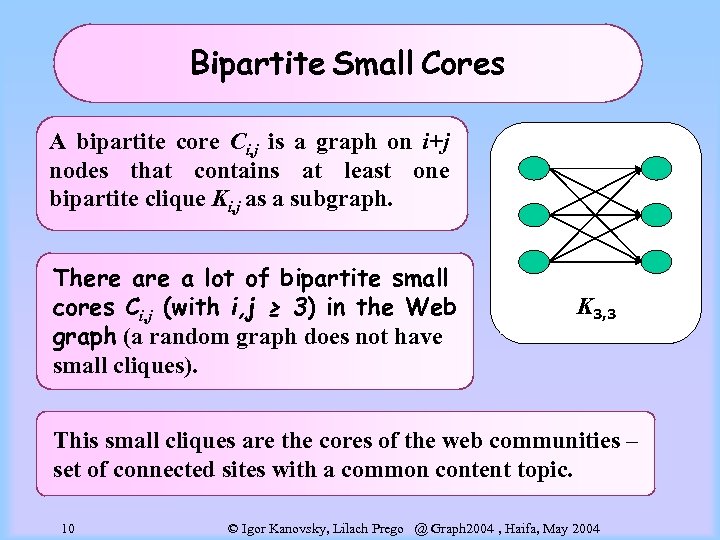Bipartite Small Cores A bipartite core Ci, j is a graph on i+j nodes that contains at least one bipartite clique Ki, j as a subgraph. There a lot of bipartite small cores Ci, j (with i, j ≥ 3) in the Web graph (a random graph does not have small cliques). K 3, 3 This small cliques are the cores of the web communities – set of connected sites with a common content topic. 10 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

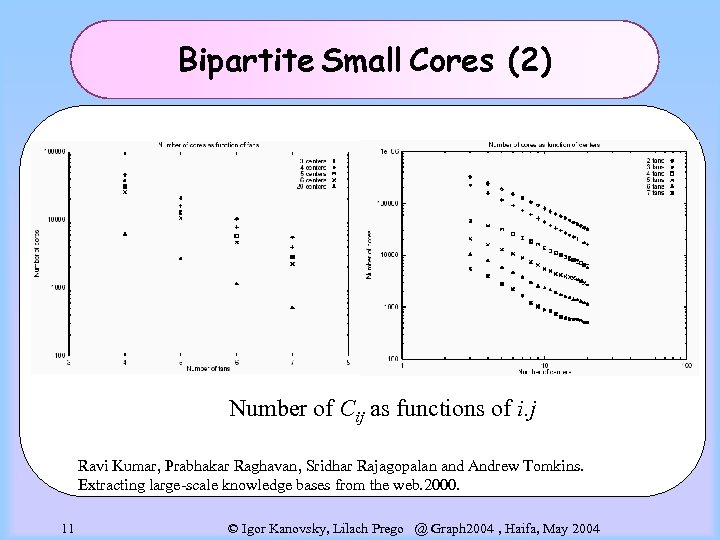Bipartite Small Cores (2) Number of Cij as functions of i. j Ravi Kumar, Prabhakar Raghavan, Sridhar Rajagopalan and Andrew Tomkins. Extracting large-scale knowledge bases from the web. 2000. 11 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

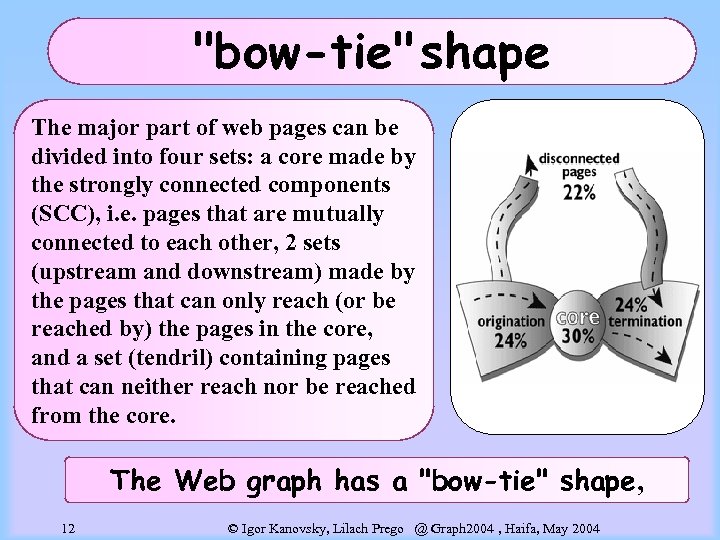"bow-tie" shape The major part of web pages can be divided into four sets: a core made by the strongly connected components (SCC), i. e. pages that are mutually connected to each other, 2 sets (upstream and downstream) made by the pages that can only reach (or be reached by) the pages in the core, and a set (tendril) containing pages that can neither reach nor be reached from the core. The Web graph has a "bow-tie" shape, 12 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Small World Graph Clustering The aim is to find subgraphs with high density of links or to find real communities in real graphs. A lot of approaches: • hub and authority method of Klienberg, • the edge betweennes method of Newman and Girwan, • local density of Virtanen, • minimum spanning tree, spectral methods, • others traditional clustering methods. Problems: how to define a cluster, how to recognise a cluster from a huge graph. 13 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Small World Graph Clustering Definition: Two vertices v 1, v 2 belongs to the same cluster if and where β -edge weighing parameter (proximity), α level of the cluster separation for a small world graph. Definition: A set of vertices belongs to cluster is called cluster. 14 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Iterated Clustering Algorithm (ICA) Input: undirected graph G=(V, E), level of cluster separation α; Output: clustering {C 1, C 2, . . . Ck}; Method: i=0; while (V is not empty){ find an arbitrary cluster C in G[V]; i++; Ci=C; V=V-C; } k=i; Advantage(!): it is not necessary to analyze all the graph to find some local clusters. 15 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Algorithm for finding an arbitrary cluster Input: undirected graph G=(V, E), level of cluster separation α; Output: A cluster. Method: ; put arbitrary vertex v into queue Q; while(Q is not empty) { get vertex u from Q; add u to C; for each { if then put w into Q; } } 16 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

ICA properties ICA has a polynomial complexity z 2 |V|, where z=|E|/ |V| average edges density, so it is applicable for real world SW graphs and it is better then other clustering algorithms rely on graph connectivity. ICA intuition is based on big clustering coefficient for SW graphs. number_of_edges_in_G[N(v)]= = 17 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

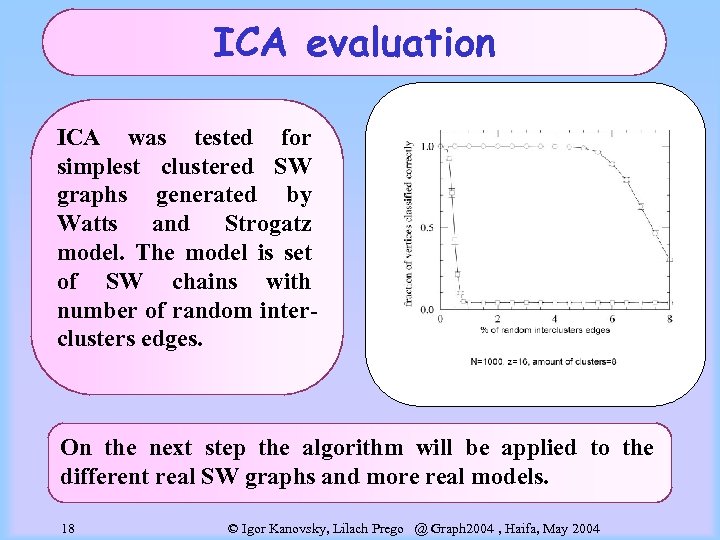ICA evaluation ICA was tested for simplest clustered SW graphs generated by Watts and Strogatz model. The model is set of SW chains with number of random interclusters edges. On the next step the algorithm will be applied to the different real SW graphs and more real models. 18 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Web-like Graph Modeling The aim is to find stochastic processes yields web-like graph. Our integrated approach is based on well known Web graph models extended in order to satisfy all mentioned above statistical properties. We try to keep a web-like graph model as simple as possible, thus it has to have a minimum set of parameters. 19 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Extended scale-free model (1) 1. At each time step, a new vertex is added and is connected to existing vertex through random number m ( z) of new edges, where the average number of edges per node (z) is constant for a growing graph. The probability that an existing vertex gains an edge is proportional to its in-degree. 20 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Extended scale-free model (2) 2. Simultaneously, z-m directed edges are distributed among all the vertices in the graph by the following rules: (i) the source is chosen with a probability proportional to their out degree, (ii) the target ends is chosen with a probability proportional to their indegree. The model has 3 parameters: average degree z, initial attractiveness of vertex to gain in and out edge Ain , Aout. 21 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

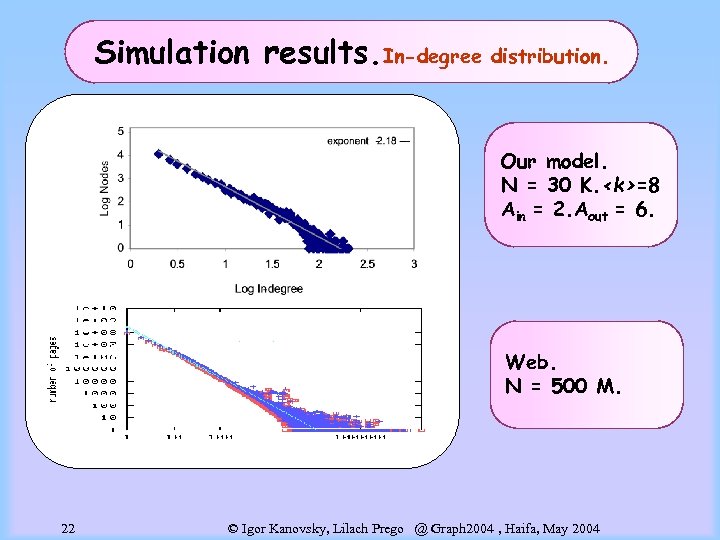Simulation results. In-degree distribution. Our model. N = 30 K. =8 Ain = 2. Aout = 6. Web. N = 500 M. 22 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

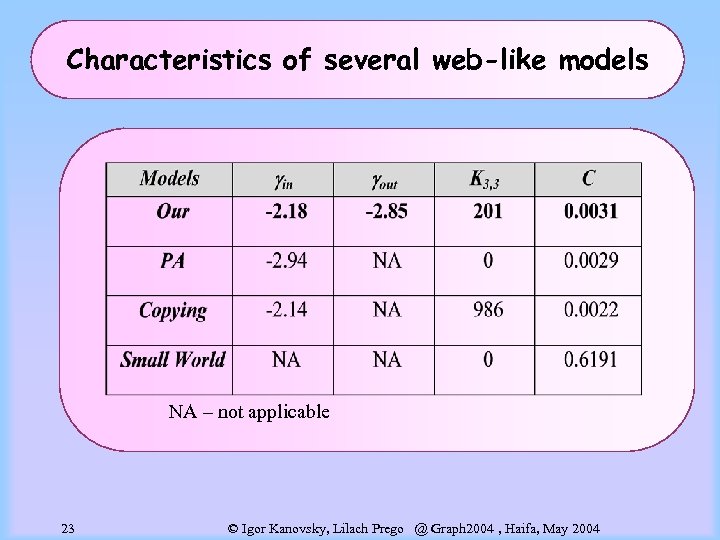Characteristics of several web-like models NA – not applicable 23 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004

Thank you. For contacts: igor kanovsky, igork@yvc. ac. il, http: //www. yvc. ac. il/ik/ 24 © Igor Kanovsky, Lilach Prego @ Graph 2004 , Haifa, May 2004