1fb02706ebe4c6c3e8b23f8b2aa6a6ce.ppt
- Количество слайдов: 25
 Clustering Uncertain Data Speaker: Ngai Wang Kay
Clustering Uncertain Data Speaker: Ngai Wang Kay
 • Data Clustering is used to discover any cluster patterns in a data set, e. g. the data set may be partitioned into several groups, or clusters, such that the data within the same cluster are closer to each other or more similar (based on some distance functions) than the data from any other clusters. • There are many methods for clustering data, and K-means clustering is a common one.
• Data Clustering is used to discover any cluster patterns in a data set, e. g. the data set may be partitioned into several groups, or clusters, such that the data within the same cluster are closer to each other or more similar (based on some distance functions) than the data from any other clusters. • There are many methods for clustering data, and K-means clustering is a common one.
 • K-means clustering considers each cluster to have a representative and it is the mean of the data in the cluster. • For an example, consider a database of location data reported from moving vehicles in a tracking system.
• K-means clustering considers each cluster to have a representative and it is the mean of the data in the cluster. • For an example, consider a database of location data reported from moving vehicles in a tracking system.
 • Given K number of location points (e. g. US White House, a school, etc. ) around the data for an initial guess of the representatives of the clusters expected to exist in the data. • K-means clustering assigns each vehicle to one of the K clusters such that its location is closer in Euclidean distance to that cluster's representative than any others' representatives.
• Given K number of location points (e. g. US White House, a school, etc. ) around the data for an initial guess of the representatives of the clusters expected to exist in the data. • K-means clustering assigns each vehicle to one of the K clusters such that its location is closer in Euclidean distance to that cluster's representative than any others' representatives.
 • Then the representative of each cluster is updated to the mean of the locations of the vehicles in the cluster. And each vehicle is reassigned to the K clusters with the new representatives. • This process repeats until some objectives is met, e. g. no changes of any vehicles' clusters between two successive processes.
• Then the representative of each cluster is updated to the mean of the locations of the vehicles in the cluster. And each vehicle is reassigned to the K clusters with the new representatives. • This process repeats until some objectives is met, e. g. no changes of any vehicles' clusters between two successive processes.
 • After the clustering, a cluster could be empty. A non-empty cluster may have some meaning, e. g. if its representative point is very close to US White House, the vehicles in the cluster may be classified as spies. • Note that if the vehicles are constantly moving, their actual locations may have changed when their reported locations data is received.
• After the clustering, a cluster could be empty. A non-empty cluster may have some meaning, e. g. if its representative point is very close to US White House, the vehicles in the cluster may be classified as spies. • Note that if the vehicles are constantly moving, their actual locations may have changed when their reported locations data is received.
 • In that case, the data in the database is not very accurate. A data will have an "uncertainty" region around it where its corresponding vehicle's actual location lies within. • The uncertainty region could be arbitrary or simply a circle region using the reported location as its center and has a radius of the vehicle's maximum speed times the time elapsed since the location data is reported.
• In that case, the data in the database is not very accurate. A data will have an "uncertainty" region around it where its corresponding vehicle's actual location lies within. • The uncertainty region could be arbitrary or simply a circle region using the reported location as its center and has a radius of the vehicle's maximum speed times the time elapsed since the location data is reported.
 • The uncertainty region could also be associated with an arbitrary probability density function (pdf) for the probability of the vehicle's actual location being in a particular point of the region. • For an example, part of the region may be sea, so the part may be associated with a total of 0. 1 probability uniformly distributed for the points in the part (for the vehicle crashes to any one of those points). A probability 0. 9 is for the vehicle to occur in any points of the remaining part of the region.
• The uncertainty region could also be associated with an arbitrary probability density function (pdf) for the probability of the vehicle's actual location being in a particular point of the region. • For an example, part of the region may be sea, so the part may be associated with a total of 0. 1 probability uniformly distributed for the points in the part (for the vehicle crashes to any one of those points). A probability 0. 9 is for the vehicle to occur in any points of the remaining part of the region.
 • Such kind of data with uncertainty is called uncertain data. • There is only few methods for clustering uncertain data. UK-means clustering is a common one. • UK-means clustering is the same as K-means clustering except its distance function is using the "expected distance" from the data's uncertainty region to the representative of the candidate cluster to whom it is assigned.
• Such kind of data with uncertainty is called uncertain data. • There is only few methods for clustering uncertain data. UK-means clustering is a common one. • UK-means clustering is the same as K-means clustering except its distance function is using the "expected distance" from the data's uncertainty region to the representative of the candidate cluster to whom it is assigned.
 • For the representative c of the cluster, an uncertainty region R with a pdf f, and a Euclidean distance function D(p, c) for any two points, the expected distance, called ed, is
• For the representative c of the cluster, an uncertainty region R with a pdf f, and a Euclidean distance function D(p, c) for any two points, the expected distance, called ed, is
 • An uncertainty region could have arbitrary shape, so the minimum bounding box (MBR) of the region is used for R. • The time complexity in UK-means clustering is O(n. K) for computing the ed values for each of n data and each of K candidate clusters. • This is very much especially for an uncertainty region with arbitrary pdf f that needs to be sampled using large number of samples in Monte Carlo methods to compute f values for the points.
• An uncertainty region could have arbitrary shape, so the minimum bounding box (MBR) of the region is used for R. • The time complexity in UK-means clustering is O(n. K) for computing the ed values for each of n data and each of K candidate clusters. • This is very much especially for an uncertainty region with arbitrary pdf f that needs to be sampled using large number of samples in Monte Carlo methods to compute f values for the points.
 • A method called Global-minmax Pruning is developed in my research to prune out some candidate clusters for a data to save some computations of ed values. • Define lmin(R, M) to be a minimum limit on the ed values computed for an uncertainty region R and a MBR M of some candidate clusters’ representative points. • Also define lmax(R, M) to be a maximum limit on the ed values computed for an uncertainty region R and a MBR M of some candidate clusters’ representative points.
• A method called Global-minmax Pruning is developed in my research to prune out some candidate clusters for a data to save some computations of ed values. • Define lmin(R, M) to be a minimum limit on the ed values computed for an uncertainty region R and a MBR M of some candidate clusters’ representative points. • Also define lmax(R, M) to be a maximum limit on the ed values computed for an uncertainty region R and a MBR M of some candidate clusters’ representative points.
 • Define minmax to be the minimum of lmax values among all candidate clusters for a data. • Then Global-minmax Pruning works like this: • A KD-tree for a given height h is built to index the representative points of the candidate clusters using p = entries in each nonleaf node. • Hence [(p^h – p) / (p – 1)] non-leaf entries.
• Define minmax to be the minimum of lmax values among all candidate clusters for a data. • Then Global-minmax Pruning works like this: • A KD-tree for a given height h is built to index the representative points of the candidate clusters using p = entries in each nonleaf node. • Hence [(p^h – p) / (p – 1)] non-leaf entries.
 • The entries in each level, except the leaf level, are sorted in increasing order in a particular dimension alternately. O((h-1) K log(K) ). • KD-tree is usually small and can be stored in CPU cache. Its access time is so little that it is ignored.
• The entries in each level, except the leaf level, are sorted in increasing order in a particular dimension alternately. O((h-1) K log(K) ). • KD-tree is usually small and can be stored in CPU cache. Its access time is so little that it is ignored.



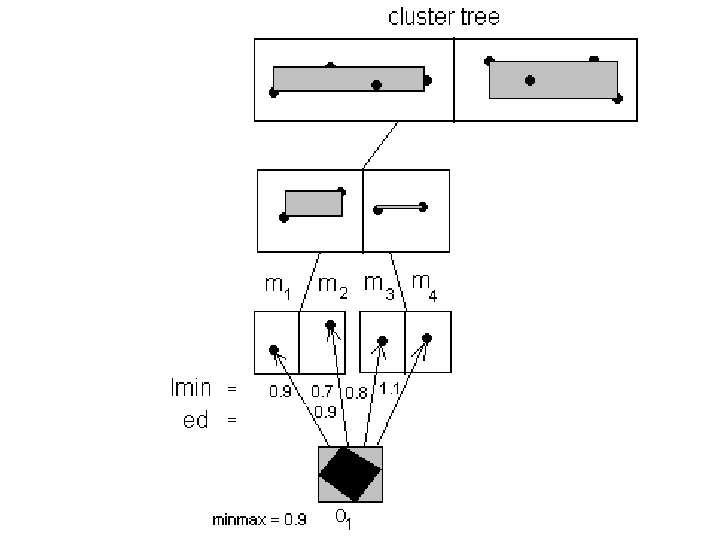

 • The time complexity for computing the ed values is then O(n. K-P) if P candidate clusters are pruned out, in average, for each object.
• The time complexity for computing the ed values is then O(n. K-P) if P candidate clusters are pruned out, in average, for each object.
 • If the KD-tree uses a capacity p for its non-leaf nodes, the worst time complexity for the pruning process is O( (h-1) K log(K) + n[2 K + (p^h – p) / (p – 1)] ) when no non-leaf entries are pruned out. • Note this is not better than the time complexity O(n. K) for computing the ed values in UKmeans clustering without any pruning if computing an ed value is not at least twice slower than computing a lmax or lmin value (e. g. for uncertainty regions with uniform pdf). • So another pruning method called Localminmax Pruning is developed in my research to address that special case.
• If the KD-tree uses a capacity p for its non-leaf nodes, the worst time complexity for the pruning process is O( (h-1) K log(K) + n[2 K + (p^h – p) / (p – 1)] ) when no non-leaf entries are pruned out. • Note this is not better than the time complexity O(n. K) for computing the ed values in UKmeans clustering without any pruning if computing an ed value is not at least twice slower than computing a lmax or lmin value (e. g. for uncertainty regions with uniform pdf). • So another pruning method called Localminmax Pruning is developed in my research to address that special case.

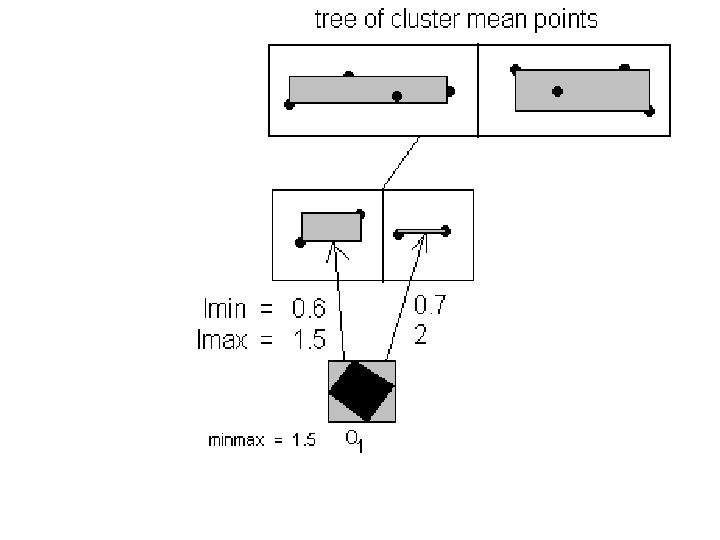
 • The worst time complexity for the pruning process is then O( (h– 1) K log(K) + n[2 K – 2 Q + 2(p^h – p) / (p – 1)] ) when Q leaf entries are pruned out before their nodes are visited. • This is better than t O( (h-1) K log(K) + n[2 K – Q + (p^h – p) / (p – 1)] ) of Global-minmax Pruning if Q > (p^h – p) / (p – 1). • This could even be better than the nonpruning method’s O(n. K) for the earlier special case of fast computation of an ed value against a lmin or lmax value if Q > [ K / 2 + (p^h – p) / (p – 1) + [(h-1) K log(K)] / 2 n ].
• The worst time complexity for the pruning process is then O( (h– 1) K log(K) + n[2 K – 2 Q + 2(p^h – p) / (p – 1)] ) when Q leaf entries are pruned out before their nodes are visited. • This is better than t O( (h-1) K log(K) + n[2 K – Q + (p^h – p) / (p – 1)] ) of Global-minmax Pruning if Q > (p^h – p) / (p – 1). • This could even be better than the nonpruning method’s O(n. K) for the earlier special case of fast computation of an ed value against a lmin or lmax value if Q > [ K / 2 + (p^h – p) / (p – 1) + [(h-1) K log(K)] / 2 n ].
 • But Local-minmax Pruning is not as effective in pruning as Global-minmax Pruning and hence could be less efficient when the computations of ed values are large overhead as its O(nk –P) increases. • Simple way to compute lmin(R, M) is to use the Euclidean distance between the two nearest points in R and M. • Simple way to compute lmax(R, M) is to use the Euclidean distance between the two farthest points in R and M.
• But Local-minmax Pruning is not as effective in pruning as Global-minmax Pruning and hence could be less efficient when the computations of ed values are large overhead as its O(nk –P) increases. • Simple way to compute lmin(R, M) is to use the Euclidean distance between the two nearest points in R and M. • Simple way to compute lmax(R, M) is to use the Euclidean distance between the two farthest points in R and M.


