3e85f20112215490f91a651e353233dd.ppt
- Количество слайдов: 159

Classification ©Jiawei Han and Micheline Kamber http: //www-sal. cs. uiuc. edu/~hanj/bk 2/ Chp 6 Integrated with slides from Prof. Andrew W. Moore http: //www. cs. cmu. edu/~awm/tutorials modified by Donghui Zhang 16 三月 2018 Data Mining: Concepts and Techniques 1

Content n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) 16 三月 2018 Data Mining: Concepts and Techniques 2

Classification vs. Prediction n Classification: n models categorical class labels (discrete or nominal) n e. g. given a new customer, does she belong to the “likely to buy a computer” class? Prediction: n models continuous-valued functions n e. g. how many computers will a customer buy? Typical Applications n credit approval n target marketing n medical diagnosis n treatment effectiveness analysis 16 三月 2018 Data Mining: Concepts and Techniques 3

Classification—A Two-Step Process n n Model construction: describing a set of predetermined classes n Each tuple/sample is assumed to belong to a predefined class, as determined by the class label attribute n The set of tuples used for model construction is training set n The model is represented as classification rules, decision trees, or mathematical formulae Model usage: for classifying future or unknown objects n Estimate accuracy of the model n The known label of test sample is compared with the classified result from the model n Accuracy rate is the percentage of test set samples that are correctly classified by the model n Test set is independent of training set, otherwise over-fitting will occur n If the accuracy is acceptable, use the model to classify data tuples whose class labels are not known 16 三月 2018 Data Mining: Concepts and Techniques 4
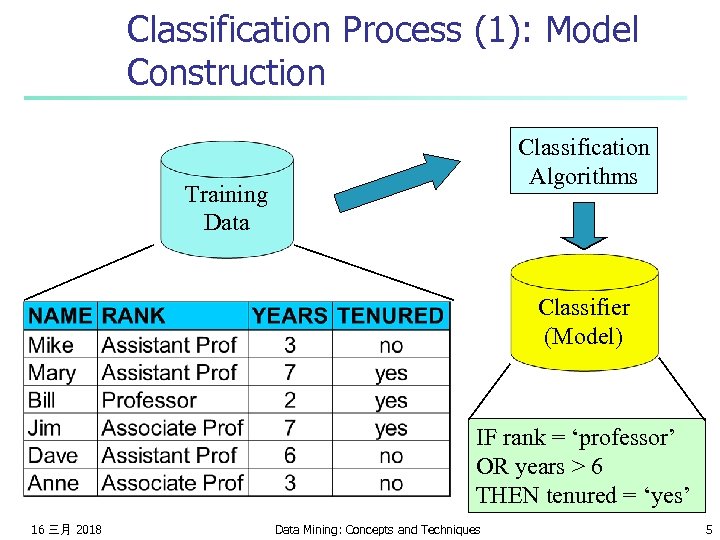
Classification Process (1): Model Construction Classification Algorithms Training Data Classifier (Model) IF rank = ‘professor’ OR years > 6 THEN tenured = ‘yes’ 16 三月 2018 Data Mining: Concepts and Techniques 5
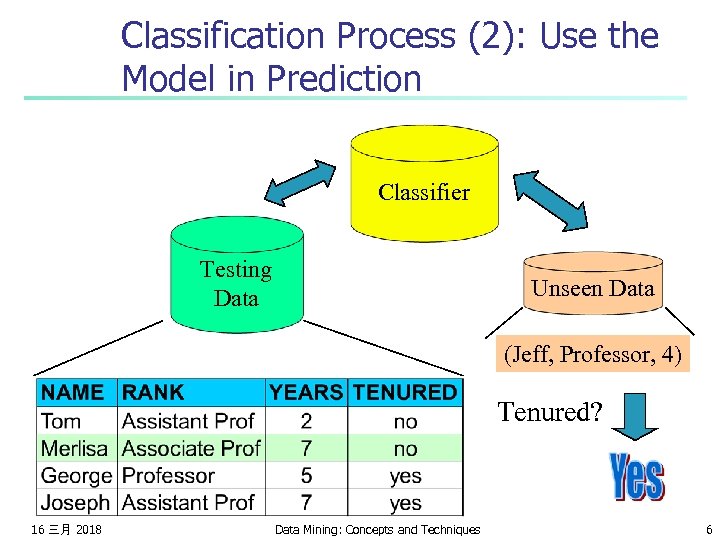
Classification Process (2): Use the Model in Prediction Classifier Testing Data Unseen Data (Jeff, Professor, 4) Tenured? 16 三月 2018 Data Mining: Concepts and Techniques 6

Supervised vs. Unsupervised Learning n Supervised learning (classification) n n n Supervision: The training data (observations, measurements, etc. ) are accompanied by labels indicating the class of the observations New data is classified based on the training set Unsupervised learning (clustering) n n 16 三月 2018 The class labels of training data is unknown Given a set of measurements, observations, etc. with the aim of establishing the existence of classes or clusters in the data Data Mining: Concepts and Techniques 7

Evaluating Classification Methods n n n Predictive accuracy Speed and scalability n time to construct the model n time to use the model Robustness n handling noise and missing values Scalability n efficiency in disk-resident databases Interpretability: n understanding and insight provided by the model Goodness of rules n decision tree size n compactness of classification rules 16 三月 2018 Data Mining: Concepts and Techniques 8

Content n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) 16 三月 2018 Data Mining: Concepts and Techniques 9
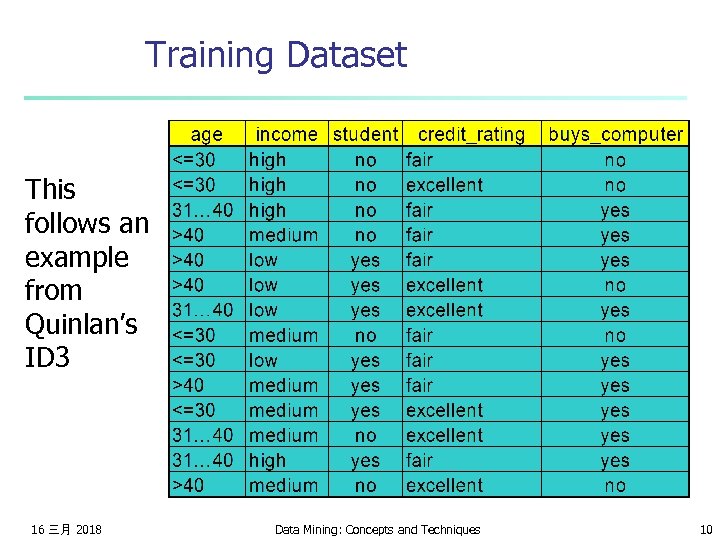
Training Dataset This follows an example from Quinlan’s ID 3 16 三月 2018 Data Mining: Concepts and Techniques 10
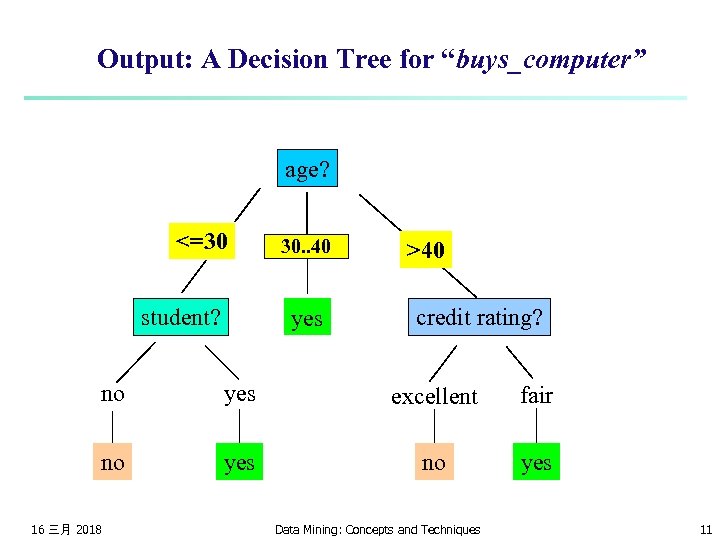
Output: A Decision Tree for “buys_computer” age? <=30 student? overcast 30. . 40 yes >40 credit rating? no yes excellent fair no yes 16 三月 2018 Data Mining: Concepts and Techniques 11

Extracting Classification Rules from Trees n Represent the knowledge in the form of IF-THEN rules n One rule is created for each path from the root to a leaf n Each attribute-value pair along a path forms a conjunction n The leaf node holds the class prediction n Rules are easier for humans to understand n Example IF age = “<=30” AND student = “no” THEN buys_computer = “no” IF age = “<=30” AND student = “yes” THEN buys_computer = “yes” IF age = “ 31… 40” THEN buys_computer = “yes” IF age = “>40” AND credit_rating = “excellent” THEN buys_computer = “yes” IF age = “<=30” AND credit_rating = “fair” THEN buys_computer = “no” 16 三月 2018 Data Mining: Concepts and Techniques 12

Algorithm for Decision Tree Induction n n Basic algorithm (a greedy algorithm) n Tree is constructed in a top-down recursive divide-and-conquer manner n At start, all the training examples are at the root n Attributes are categorical (if continuous-valued, they are discretized in advance) n Examples are partitioned recursively based on selected attributes n Test attributes are selected on the basis of a heuristic or statistical measure (e. g. , information gain) Conditions for stopping partitioning n All samples for a given node belong to the same class n There are no remaining attributes for further partitioning – majority voting is employed for classifying the leaf n There are no samples left 16 三月 2018 Data Mining: Concepts and Techniques 13

Note to other teachers and users of these slides. Andrew would be delighted if you found this source material useful in giving your own lectures. Feel free to use these slides verbatim, or to modify them to fit your own needs. Power. Point originals are available. If you make use of a significant portion of these slides in your own lecture, please include this message, or the following link to the source repository of Andrew’s tutorials: http: //www. cs. cmu. edu/~awm/tutorials. Comments and corrections gratefully received. Information gain slides adapted from Andrew W. Moore Associate Professor School of Computer Science Carnegie Mellon University www. cs. cmu. edu/~awm awm@cs. cmu. edu 412 -268 -7599 16 三月 2018 Data Mining: Concepts and Techniques 14

Bits You are watching a set of independent random samples of X You see that X has four possible values P(X=A) = 1/4 P(X=B) = 1/4 P(X=C) = 1/4 P(X=D) = 1/4 So you might see: BAACBADCDADDDA… You transmit data over a binary serial link. You can encode each reading with two bits (e. g. A = 00, B = 01, C = 10, D = 11) 0100001001001110110011111100… 16 三月 2018 Data Mining: Concepts and Techniques 15

Fewer Bits Someone tells you that the probabilities are not equal P(X=A) = 1/2 P(X=B) = 1/4 P(X=C) = 1/8 P(X=D) = 1/8 It’s possible… …to invent a coding for your transmission that only uses 1. 75 bits on average per symbol. How? 16 三月 2018 Data Mining: Concepts and Techniques 16

Fewer Bits Someone tells you that the probabilities are not equal P(X=A) = 1/2 P(X=B) = 1/4 P(X=C) = 1/8 P(X=D) = 1/8 It’s possible… …to invent a coding for your transmission that only uses 1. 75 bits on average per symbol. How? A 0 B 10 C 110 D 111 (This is just one of several ways) 16 三月 2018 Data Mining: Concepts and Techniques 17

Fewer Bits Suppose there are three equally likely values… P(X=B) = 1/3 P(X=C) = 1/3 P(X=D) = 1/3 Here’s a naïve coding, costing 2 bits per symbol A 00 B 01 C 10 Can you think of a coding that would need only 1. 6 bits per symbol on average? In theory, it can in fact be done with 1. 58496 bits per symbol. 16 三月 2018 Data Mining: Concepts and Techniques 18
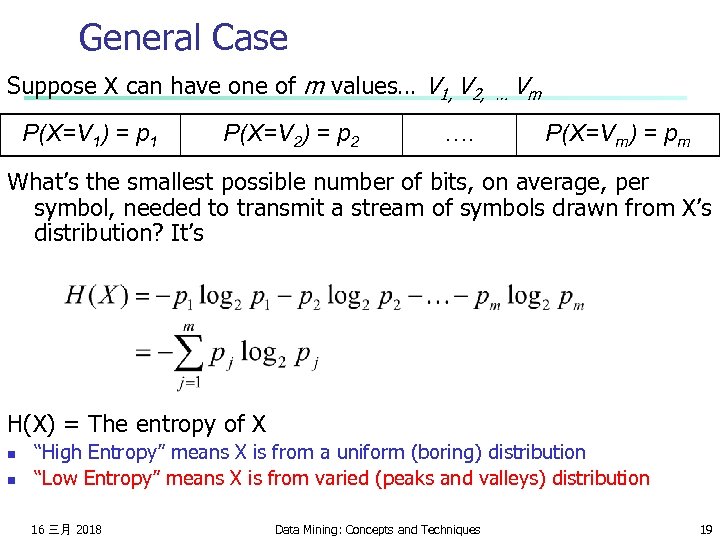
General Case Suppose X can have one of m values… V 1, V 2, P(X=V 1) = p 1 P(X=V 2) = p 2 …. … Vm P(X=Vm) = pm What’s the smallest possible number of bits, on average, per symbol, needed to transmit a stream of symbols drawn from X’s distribution? It’s H(X) = The entropy of X n n “High Entropy” means X is from a uniform (boring) distribution “Low Entropy” means X is from varied (peaks and valleys) distribution 16 三月 2018 Data Mining: Concepts and Techniques 19

General Case Suppose X can have one of m values… V 1, V 2, P(X=V 1) = p 1 P(X=V 2) = p 2 …. … Vm P(X=Vm) = pm A histogram of the What’s the smallest possible number of bits, on average, per frequency distribution of symbol, needed to transmit a stream of symbols drawn from X’s values of X would have A histogram of the distribution? It’s many lows and one or frequency distribution of two highs values of X would be flat H(X) = The entropy of X n n “High Entropy” means X is from a uniform (boring) distribution “Low Entropy” means X is from varied (peaks and valleys) distribution 16 三月 2018 Data Mining: Concepts and Techniques 20

General Case Suppose X can have one of m values… V 1, V 2, P(X=V 1) = p 1 P(X=V 2) = p 2 …. … Vm P(X=Vm) = pm A histogram of the What’s the smallest possible number of bits, on average, per frequency distribution of symbol, needed to transmit a stream of symbols drawn from X’s values of X would have A histogram of the distribution? It’s many lows and one or frequency distribution of two highs values of X would be flat. . and so the values sampled from it would be all over the place H(X) = The entropy of X n n . . and so the values sampled from it would be more predictable “High Entropy” means X is from a uniform (boring) distribution “Low Entropy” means X is from varied (peaks and valleys) distribution 16 三月 2018 Data Mining: Concepts and Techniques 21

Entropy in a nut-shell Low Entropy 16 三月 2018 High Entropy Data Mining: Concepts and Techniques 22

Entropy in a nut-shell Low Entropy High Entropy. . the values (locations of soup) sampled entirely from within the soup bowl 16 三月 2018 . . the values (locations of soup) unpredictable. . . almost uniformly sampled throughout our dining room Data Mining: Concepts and Techniques 23

Exercise: n n n Suppose 100 customers have two classes: “Buy Computer” and “Not Buy Computer”. Uniform distribution: 50 buy. Entropy? Skewed distribution: 100 buy. Entropy? 16 三月 2018 Data Mining: Concepts and Techniques 24

Specific Conditional Entropy Suppose I’m trying to predict output Y and I have input X X = College Major Y = Likes “Gladiator” X Y Let’s assume this reflects the true probabilities E. G. From this data we estimate Math Yes • P(Like. G = Yes) = 0. 5 History No CS Yes • P(Major = Math & Like. G = No) = 0. 25 Math No CS Yes History No Math Yes 16 三月 2018 • P(Major = Math) = 0. 5 • P(Like. G = Yes | Major = History) = 0 Note: • H(X) = 1. 5 • H(Y) = 1 Data Mining: Concepts and Techniques 25

Specific Conditional Entropy X = College Major Y = Likes “Gladiator” X Y Math Yes History Yes Math No CS Yes History No Math H(Y|X=v) = The entropy of Y among only those records in which X has value v No CS Definition of Specific Conditional Entropy: Yes 16 三月 2018 Data Mining: Concepts and Techniques 26

Specific Conditional Entropy X = College Major Definition of Conditional Entropy: Y = Likes “Gladiator” H(Y|X=v) = The entropy of Y among only those records in which X has value v X Y Example: Math Yes History No CS Yes • H(Y|X=Math) = 1 Math No • H(Y|X=History) = 0 Math No • H(Y|X=CS) = 0 CS Yes History No Math Yes 16 三月 2018 Data Mining: Concepts and Techniques 27

Conditional Entropy X = College Major Y = Likes “Gladiator” X Y Math Yes History No CS Yes Math No CS Yes History No Math Yes Definition of Specific Conditional Entropy: H(Y|X) = The average conditional entropy of Y = if you choose a record at random what will be the conditional entropy of Y, conditioned on that row’s value of X = Expected number of bits to transmit Y if both sides will know the value of X = Σj. Prob(X=vj) H(Y | X = vj) 16 三月 2018 Data Mining: Concepts and Techniques 28

Conditional Entropy Definition of general Conditional Y = Likes “Gladiator” Entropy: X = College Major H(Y|X) = The average conditional entropy of Y X Y Math Yes History No CS Yes Math No CS Yes History Yes Example: No Math = Σj. Prob(X=vj) H(Y | X = vj) 16 三月 2018 vj Math History CS Prob(X=vj) 0. 5 0. 25 H(Y | X = vj) 1 0 0 H(Y|X) = 0. 5 * 1 + 0. 25 * 0 = 0. 5 Data Mining: Concepts and Techniques 29

Information Gain X = College Major Y = Likes “Gladiator” X Y Definition of Information Gain: IG(Y|X) = I must transmit Y. How many bits on average would it save me if both ends of the line knew X? IG(Y|X) = H(Y) - H(Y | X) Math Yes History No CS Yes Math No CS Yes • H(Y|X) = 0. 5 History No Math Yes • Thus IG(Y|X) = 1 – 0. 5 = 0. 5 16 三月 2018 Example: • H(Y) = 1 Data Mining: Concepts and Techniques 30

What is Information Gain used for? Suppose you are trying to predict whether someone is going live past 80 years. From historical data you might find… • IG(Long. Life | Hair. Color) = 0. 01 • IG(Long. Life | Smoker) = 0. 2 • IG(Long. Life | Gender) = 0. 25 • IG(Long. Life | Last. Digit. Of. SSN) = 0. 00001 IG tells you how interesting a 2 -d contingency table is going to be. 16 三月 2018 Data Mining: Concepts and Techniques 31

Conditional entropy H(C|age) n n n H(C|age<=30) = 2/5 * lg(5/2) + 3/5 * lg(5/3) = 0. 971 H(C|age in 30. . 40) = 1 * lg 1 + 0 * lg 1/0 = 0 H(C|age>40) = 3/5 * lg(5/3) + 2/5 * lg(5/2) = 0. 971 16 三月 2018 Data Mining: Concepts and Techniques 32

Select the attribute with lowest conditional entropy n n n H(C|age) = 0. 694 H(C|income) = 0. 911 H(C|student) = 0. 789 H(C|credit_rating) = 0. 892 age? 30. . 40 Select “age” to be the <=30 tree root! student? yes no no 16 三月 2018 yes Data Mining: Concepts and Techniques >40 credit rating? excellent fair no yes 33

Goodness in Decision Tree Induction n n relatively faster learning speed (than other classification methods) convertible to simple and easy to understand classification rules can use SQL queries for accessing databases comparable classification accuracy with other methods 16 三月 2018 Data Mining: Concepts and Techniques 34

Scalable Decision Tree Induction Methods in Data Mining Studies n n SLIQ (EDBT’ 96 — Mehta et al. ) n builds an index for each attribute and only class list and the current attribute list reside in memory SPRINT (VLDB’ 96 — J. Shafer et al. ) n constructs an attribute list data structure PUBLIC (VLDB’ 98 — Rastogi & Shim) n integrates tree splitting and tree pruning: stop growing the tree earlier Rain. Forest (VLDB’ 98 — Gehrke, Ramakrishnan & Ganti) n separates the scalability aspects from the criteria that determine the quality of the tree n builds an AVC-list (attribute, value, class label) 16 三月 2018 Data Mining: Concepts and Techniques 35
Visualization of a Decision Tree in SGI/Mine. Set 3. 0 16 三月 2018 Data Mining: Concepts and Techniques 36

Content n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) 16 三月 2018 Data Mining: Concepts and Techniques 37

Bayesian Classification: Why? n n Probabilistic learning: Calculate explicit probabilities for hypothesis, among the most practical approaches to certain types of learning problems Incremental: Each training example can incrementally increase/decrease the probability that a hypothesis is correct. Prior knowledge can be combined with observed data. Probabilistic prediction: Predict multiple hypotheses, weighted by their probabilities Standard: Even when Bayesian methods are computationally intractable, they can provide a standard of optimal decision making against which other methods can be measured 16 三月 2018 Data Mining: Concepts and Techniques 38

Bayesian Classification n n n X: a data sample whose class label is unknown, e. g. X =(Income=medium, Credit_rating=Fair, Age=40). Hi: a hypothesis that a record belongs to class Ci, e. g. Hi = a record belongs to the “buy computer” class. P(Hi), P(X): probabilities. P(Hi/X): a conditional probability: among all records with medium income and fair credit rating, what’s the probability to buy a computer? This is what we need for classification! Given X, P(Hi/X) tells us the possibility that it belongs to some class. What if we need to determine a single class for X? 16 三月 2018 Data Mining: Concepts and Techniques 39

Bayesian Theorem n n Another concept, P(X|Hi) : probability of observing the sample X, given that the hypothesis holds. E. g. among all people who buy computer, what percentage has the same value as X. We know P(X Hi) = P(Hi|X) P(X) = P(X|Hi) P(Hi), So We should assign X to the class Ci where P(Hi|X) is maximized, n equivalent to maximize P(X|Hi) P(Hi). 16 三月 2018 Data Mining: Concepts and Techniques 40

Basic Idea n n n Read the training data, n Compute P(Hi) for each class. n Compute P(Xk|Hi) for each distinct instance of X among records in class Ci. To predict the class for a new data X, n for each class, compute P(X|Hi) P(Hi). n return the class which has the largest value. Any Problem? Too many combinations of Xk. e. g. 50 ages, 50 credit ratings, 50 income levels 125, 000 combinations of Xk! 16 三月 2018 Data Mining: Concepts and Techniques 41

Naïve Bayes Classifier n n A simplified assumption: attributes are conditionally independent: The product of occurrence of say 2 elements x 1 and x 2, given the current class is C, is the product of the probabilities of each element taken separately, given the same class P([y 1, y 2], C) = P(y 1, C) * P(y 2, C) No dependence relation between attributes Greatly reduces the number of probabilities to maintain. 16 三月 2018 Data Mining: Concepts and Techniques 42
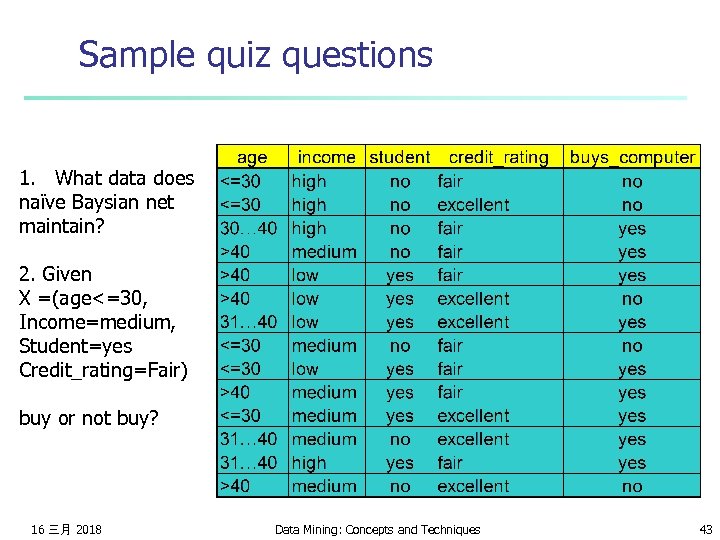
Sample quiz questions 1. What data does naïve Baysian net maintain? 2. Given X =(age<=30, Income=medium, Student=yes Credit_rating=Fair) buy or not buy? 16 三月 2018 Data Mining: Concepts and Techniques 43

Naïve Bayesian Classifier: Example n Compute P(X/Ci) for each class P(age=“<30” | buys_computer=“yes”) = 2/9=0. 222 P(age=“<30” | buys_computer=“no”) = 3/5 =0. 6 P(income=“medium” | buys_computer=“yes”)= 4/9 =0. 444 P(income=“medium” | buys_computer=“no”) = 2/5 = 0. 4 P(student=“yes” | buys_computer=“yes)= 6/9 =0. 667 P(student=“yes” | buys_computer=“no”)= 1/5=0. 2 P(credit_rating=“fair” | buys_computer=“yes”)=6/9=0. 667 P(credit_rating=“fair” | buys_computer=“no”)=2/5=0. 4 X=(age<=30 , income =medium, student=yes, credit_rating=fair) P(X|Ci) : P(X|buys_computer=“yes”)= 0. 222 x 0. 444 x 0. 667 x 0. 0. 667 =0. 044 P(X|buys_computer=“no”)= 0. 6 x 0. 4 x 0. 2 x 0. 4 =0. 019 P(X|Ci)*P(Ci ) : P(X|buys_computer=“yes”) * P(buys_computer=“yes”)=0. 028 P(X|buys_computer=“no”) * P(buys_computer=“no”)=0. 007 X belongs to class “buys_computer=yes” 16 三月 2018 Pitfall: forget P(Ci) Data Mining: Concepts and Techniques 44

Naïve Bayesian Classifier: Comments n n n Advantages : n Easy to implement n Good results obtained in most of the cases Disadvantages n Assumption: class conditional independence , therefore loss of accuracy n Practically, dependencies exist among variables n E. g. , hospitals: patients: Profile: age, family history etc Symptoms: fever, cough etc. , Disease: lung cancer, diabetes etc n Dependencies among these cannot be modeled by Naïve Bayesian Classifier How to deal with these dependencies? n Bayesian Belief Networks 16 三月 2018 Data Mining: Concepts and Techniques 45

Content n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) 16 三月 2018 Data Mining: Concepts and Techniques 46

Note to other teachers and users of these slides. Andrew would be delighted if you found this source material useful in giving your own lectures. Feel free to use these slides verbatim, or to modify them to fit your own needs. Power. Point originals are available. If you make use of a significant portion of these slides in your own lecture, please include this message, or the following link to the source repository of Andrew’s tutorials: http: //www. cs. cmu. edu/~awm/tutorials. Comments and corrections gratefully received. Baysian Networks slides adapted from Andrew W. Moore Associate Professor School of Computer Science Carnegie Mellon University www. cs. cmu. edu/~awm awm@cs. cmu. edu 412 -268 -7599 16 三月 2018 Data Mining: Concepts and Techniques 47

What we’ll discuss n n n Recall the numerous and dramatic benefits of Joint Distributions for describing uncertain worlds Reel with terror at the problem with using Joint Distributions Discover how Bayes Net methodology allows us to build Joint Distributions in manageable chunks Discover there’s still a lurking problem… …Start to solve that problem 16 三月 2018 Data Mining: Concepts and Techniques 48

Why this matters In Andrew’s opinion, the most important technology in the Machine Learning / AI field to Active Data have emerged in the last 10 years. Collection n A clean, clear, manageable language and methodology for expressing what you’re certain Inference and uncertain about n Already, many practical applications in medicine, Anomaly factories, helpdesks: Detection n P(this problem | these symptoms) anomalousness of this observation choosing next diagnostic test | these observations 16 三月 2018 Data Mining: Concepts and Techniques 49

Ways to deal with Uncertainty n n n Three-valued logic: True / False / Maybe Fuzzy logic (truth values between 0 and 1) Non-monotonic reasoning (especially focused on Penguin informatics) Dempster-Shafer theory (and an extension known as quasi-Bayesian theory) Possibabilistic Logic Probability 16 三月 2018 Data Mining: Concepts and Techniques 50

Discrete Random Variables n n n A is a Boolean-valued random variable if A denotes an event, and there is some degree of uncertainty as to whether A occurs. Examples A = The US president in 2023 will be male A = You wake up tomorrow with a headache A = You have Ebola 16 三月 2018 Data Mining: Concepts and Techniques 51

Probabilities n n n We write P(A) as “the fraction of possible worlds in which A is true” We could at this point spend 2 hours on the philosophy of this. But we won’t. 16 三月 2018 Data Mining: Concepts and Techniques 52
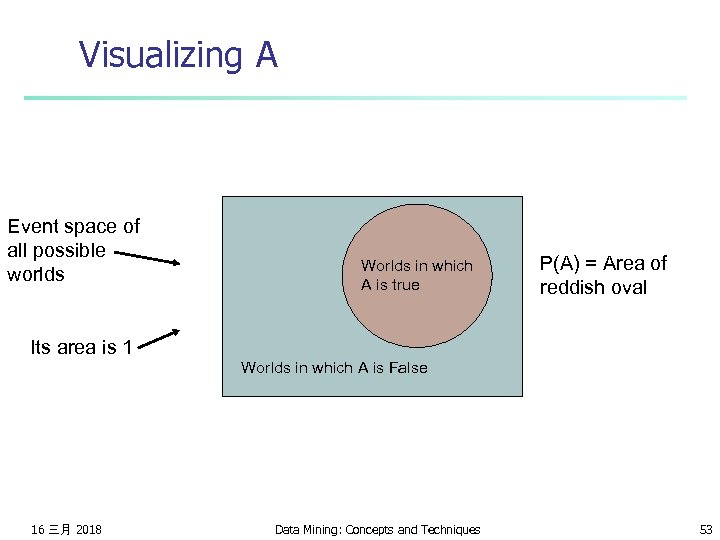
Visualizing A Event space of all possible worlds Worlds in which A is true P(A) = Area of reddish oval Its area is 1 Worlds in which A is False 16 三月 2018 Data Mining: Concepts and Techniques 53

Interpreting the axioms n n 0 <= P(A) <= 1 P(True) = 1 P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) The area of A can’t get any smaller than 0 And a zero area would mean no world could ever have A true 16 三月 2018 Data Mining: Concepts and Techniques 54

Interpreting the axioms n n 0 <= P(A) <= 1 P(True) = 1 P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) The area of A can’t get any bigger than 1 And an area of 1 would mean all worlds will have A true 16 三月 2018 Data Mining: Concepts and Techniques 55

Interpreting the axioms n n 0 <= P(A) <= 1 P(True) = 1 P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) A B 16 三月 2018 Data Mining: Concepts and Techniques 56
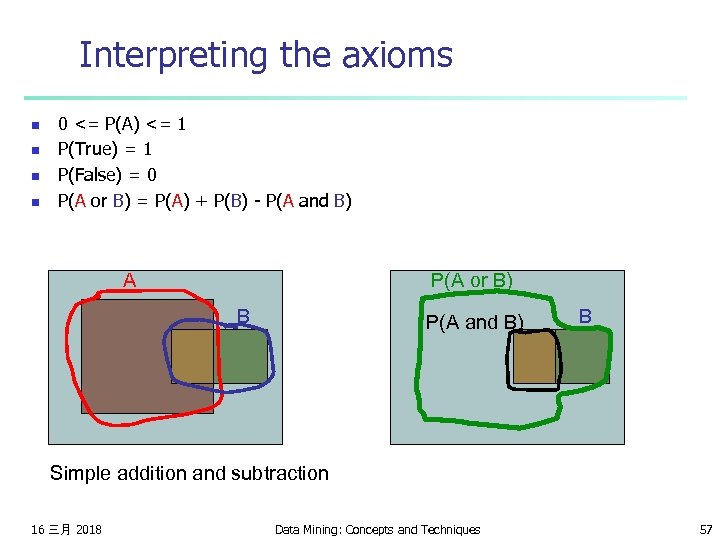
Interpreting the axioms n n 0 <= P(A) <= 1 P(True) = 1 P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) A P(A or B) B P(A and B) B Simple addition and subtraction 16 三月 2018 Data Mining: Concepts and Techniques 57

These Axioms are Not to be Trifled With n There have been attempts to do different methodologies for uncertainty n n n Fuzzy Logic Three-valued logic Dempster-Shafer Non-monotonic reasoning But the axioms of probability are the only system with this property: If you gamble using them you can’t be unfairly exploited by an opponent using some other system [di Finetti 1931] 16 三月 2018 Data Mining: Concepts and Techniques 58

Theorems from the Axioms n n 0 <= P(A) <= 1, P(True) = 1, P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) From these we can prove: P(not A) = P(~A) = 1 -P(A) n How? 16 三月 2018 Data Mining: Concepts and Techniques 59

Another important theorem n n 0 <= P(A) <= 1, P(True) = 1, P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) From these we can prove: P(A) = P(A ^ B) + P(A ^ ~B) n How? 16 三月 2018 Data Mining: Concepts and Techniques 60

Conditional Probability n P(A|B) = Fraction of worlds in which B is true that also have A true H = “Have a headache” F = “Coming down with Flu” P(H) = 1/10 P(F) = 1/40 P(H|F) = 1/2 F H 16 三月 2018 “Headaches are rare and flu is rarer, but if you’re coming down with ‘flu there’s a 5050 chance you’ll have a headache. ” Data Mining: Concepts and Techniques 61

Conditional Probability P(H|F) = Fraction of flu-inflicted worlds in which you have a headache F H = #worlds with flu and headache ------------------#worlds with flu H = “Have a headache” F = “Coming down with Flu” P(H) = 1/10 P(F) = 1/40 P(H|F) = 1/2 16 三月 2018 = Area of “H and F” region ---------------Area of “F” region = P(H ^ F) -----P(F) Data Mining: Concepts and Techniques 62

Definition of Conditional Probability P(A ^ B) P(A|B) = -----P(B) Corollary: The Chain Rule P(A ^ B) = P(A|B) P(B) 16 三月 2018 Data Mining: Concepts and Techniques 63

Bayes Rule P(A ^ B) P(A|B) P(B|A) = -------------- P(A) This is Bayes Rule Bayes, Thomas (1763) An essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society of London, 53: 370418 16 三月 2018 Data Mining: Concepts and Techniques 64

Using Bayes Rule to Gamble R R B B $1. 00 The “Win” envelope has a dollar and four beads in it R B B The “Lose” envelope has three beads and no money Trivial question: someone draws an envelope at random and offers to sell it to you. How much should you pay? 16 三月 2018 Data Mining: Concepts and Techniques 65

Using Bayes Rule to Gamble $1. 00 The “Win” envelope has a dollar and four beads in it The “Lose” envelope has three beads and no money Interesting question: before deciding, you are allowed to see one bead drawn from the envelope. Suppose it’s black: How much should you pay? Suppose it’s red: How much should you pay? 16 三月 2018 Data Mining: Concepts and Techniques 66

Another Example n n You friend told you that she has two children (not twin). n Probability that both children are male? You asked her whether she has at least one son, and she said yes. n Probability that both children are male? You visited her house and saw one son of hers. n Probability that both children are male? Note: P(See. ASon|One. Son) and P(Tell. ASon|One. Son) are different! 16 三月 2018 Data Mining: Concepts and Techniques 67

Multivalued Random Variables n n n Suppose A can take on more than 2 values A is a random variable with arity k if it can take on exactly one value out of {v 1, v 2, . . vk} Thus… 16 三月 2018 Data Mining: Concepts and Techniques 68

An easy fact about Multivalued Random Variables: n Using the axioms of probability… 0 <= P(A) <= 1, P(True) = 1, P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) n And assuming that A obeys… • It’s easy to prove that 16 三月 2018 Data Mining: Concepts and Techniques 69

An easy fact about Multivalued Random Variables: n Using the axioms of probability… 0 <= P(A) <= 1, P(True) = 1, P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) n And assuming that A obeys… • It’s easy to prove that • And thus we can prove 16 三月 2018 Data Mining: Concepts and Techniques 70

Another fact about Multivalued Random Variables: n Using the axioms of probability… 0 <= P(A) <= 1, P(True) = 1, P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) n And assuming that A obeys… • It’s easy to prove that 16 三月 2018 Data Mining: Concepts and Techniques 71

Another fact about Multivalued Random Variables: n Using the axioms of probability… 0 <= P(A) <= 1, P(True) = 1, P(False) = 0 P(A or B) = P(A) + P(B) - P(A and B) n And assuming that A obeys… • It’s easy to prove that • And thus we can prove 16 三月 2018 Data Mining: Concepts and Techniques 72

More General Forms of Bayes Rule 16 三月 2018 Data Mining: Concepts and Techniques 73

More General Forms of Bayes Rule 16 三月 2018 Data Mining: Concepts and Techniques 74

Useful Easy-to-prove facts 16 三月 2018 Data Mining: Concepts and Techniques 75

From Probability to Bayesian Net • Suppose there are some diseases, symptoms and related facts. • E. g. flu, headache, fever, lung cancer, smoker. • We are interested to know some (conditional or unconditional) probabilities such as • P( flu ) • P( lung cancer | smoker ) • P( flu | headache ^ ~fever ) • What shall we do? 16 三月 2018 Data Mining: Concepts and Techniques 76

The Joint Distribution Example: Boolean variables A, B, C Recipe for making a joint distribution of M variables: 16 三月 2018 Data Mining: Concepts and Techniques 77

The Joint Distribution Recipe for making a joint distribution of M variables: 1. Make a truth table listing all combinations of values of your variables (if there are M Boolean variables then the table will have 2 M rows). 16 三月 2018 Example: Boolean variables A, B, C A B C 0 0 0 1 1 1 0 0 1 1 1 Data Mining: Concepts and Techniques 78
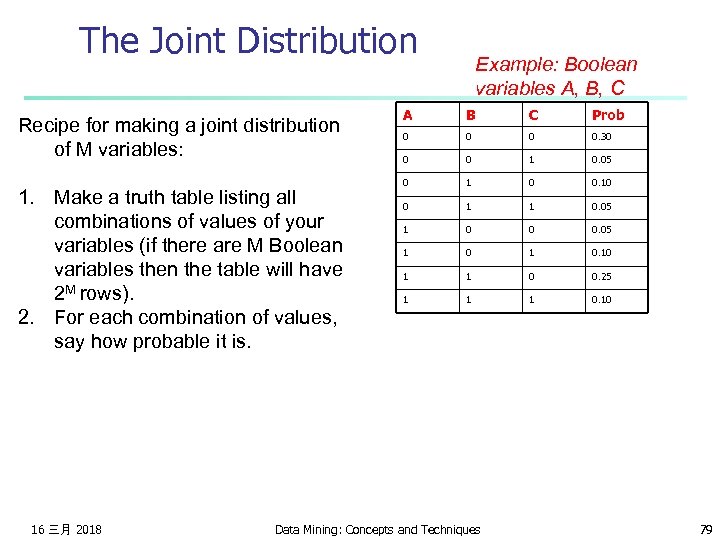
The Joint Distribution Recipe for making a joint distribution of M variables: 1. Make a truth table listing all combinations of values of your variables (if there are M Boolean variables then the table will have 2 M rows). 2. For each combination of values, say how probable it is. 16 三月 2018 Example: Boolean variables A, B, C A B C Prob 0 0. 30 0 0 1 0. 05 0 1 0 0. 10 0 1 1 0. 05 1 0 0 0. 05 1 0. 10 1 1 0 0. 25 1 1 1 0. 10 Data Mining: Concepts and Techniques 79

The Joint Distribution Recipe for making a joint distribution of M variables: 1. Make a truth table listing all combinations of values of your variables (if there are M Boolean variables then the table will have 2 M rows). 2. For each combination of values, say how probable it is. 3. If you subscribe to the axioms of probability, those numbers must sum to 1. Example: Boolean variables A, B, C A B C Prob 0 0. 30 0 0 1 0. 05 0 1 0 0. 10 0 1 1 0. 05 1 0 0 0. 05 1 0. 10 1 1 0 0. 25 1 1 1 0. 10 A 0. 25 0. 30 16 三月 2018 0. 05 B Data Mining: Concepts and Techniques 0. 10 0. 05 C 0. 10 80
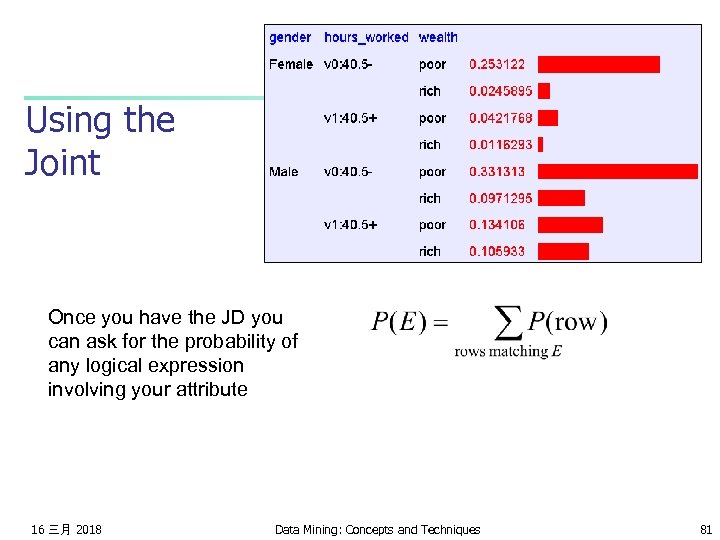
Using the Joint Once you have the JD you can ask for the probability of any logical expression involving your attribute 16 三月 2018 Data Mining: Concepts and Techniques 81
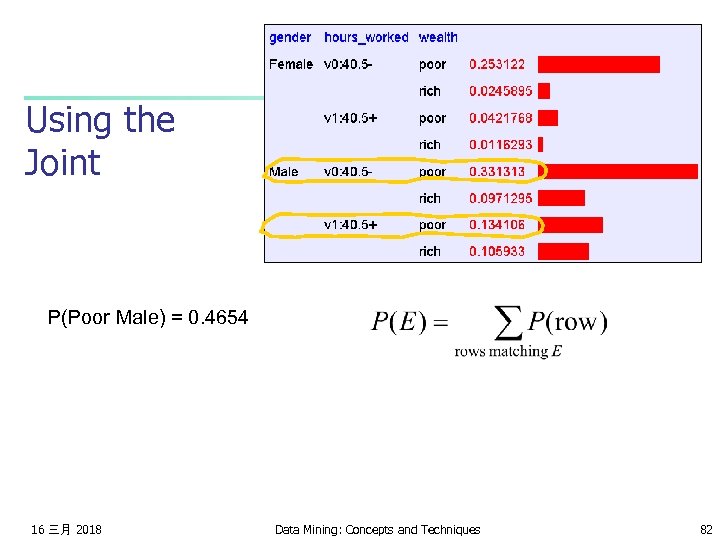
Using the Joint P(Poor Male) = 0. 4654 16 三月 2018 Data Mining: Concepts and Techniques 82
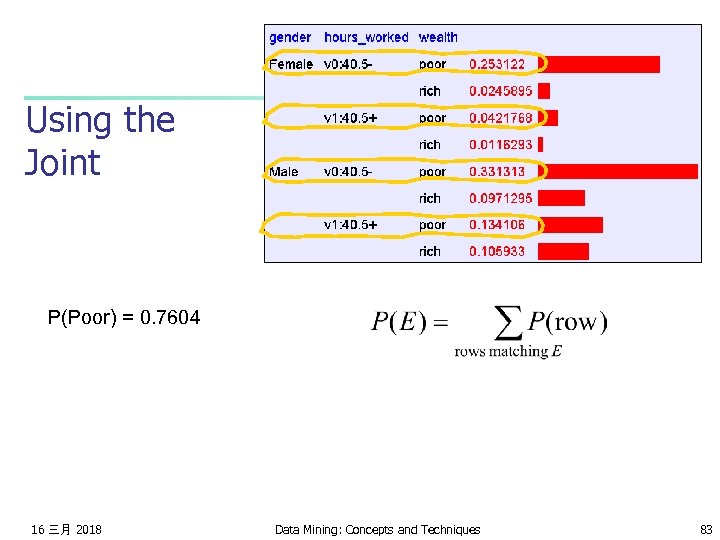
Using the Joint P(Poor) = 0. 7604 16 三月 2018 Data Mining: Concepts and Techniques 83

Inference with the Joint 16 三月 2018 Data Mining: Concepts and Techniques 84
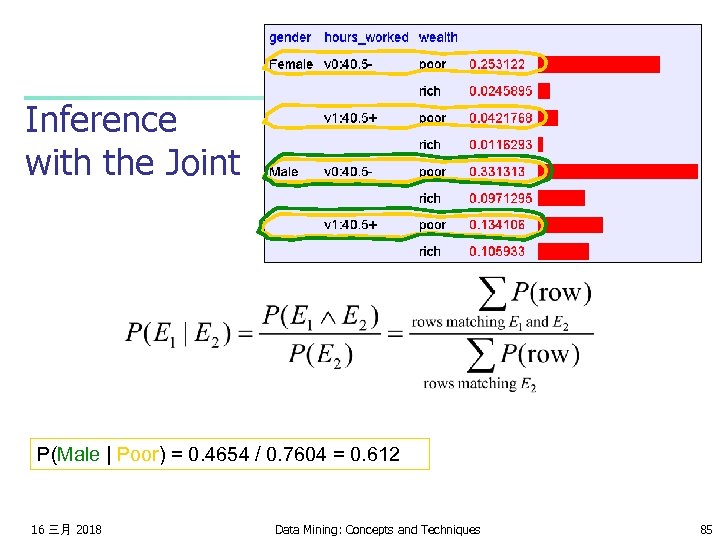
Inference with the Joint P(Male | Poor) = 0. 4654 / 0. 7604 = 0. 612 16 三月 2018 Data Mining: Concepts and Techniques 85

Joint distributions n Good news n Once you have a joint distribution, you can ask important questions about stuff that involves a lot of uncertainty 16 三月 2018 Bad news Impossible to create for more than about ten attributes because there are so many numbers needed when you build the damn thing. Data Mining: Concepts and Techniques 86

Using fewer numbers Suppose there are two events: n n M: Manuela teaches the class (otherwise it’s Andrew) S: It is sunny The joint p. d. f. for these events contain four entries. If we want to build the joint p. d. f. we’ll have to invent those four numbers. OR WILL WE? ? n n We don’t have to specify with bottom level conjunctive events such as P(~M^S) IF… …instead it may sometimes be more convenient for us to specify things like: P(M), P(S). But just P(M) and P(S) don’t derive the joint distribution. So you can’t answer all questions. 16 三月 2018 Data Mining: Concepts and Techniques 87

Using fewer numbers Suppose there are two events: n n M: Manuela teaches the class (otherwise it’s Andrew) S: It is sunny The joint p. d. f. for these events contain four entries. If we want to build the joint p. d. f. we’ll have to invent those four numbers. OR WILL WE? ? We don’t have to specify with bottom level conjunctive events such as P(~M^S) IF… n …instead it may sometimes be more convenient for us to specify things like: P(M), P(S). Wha But just P(M) and P(S) don’t derive the joint distribution. So you can’t mak t extra a e? answer all questions. ssump tion can you n 16 三月 2018 Data Mining: Concepts and Techniques 88

Independence “The sunshine levels do not depend on and do not influence who is teaching. ” This can be specified very simply: P(S M) = P(S) This is a powerful statement! It required extra domain knowledge. A different kind of knowledge than numerical probabilities. It needed an understanding of causation. 16 三月 2018 Data Mining: Concepts and Techniques 89

Independence From P(S M) = P(S), the rules of probability imply: (can you prove these? ) n P(~S M) = P(~S) n P(M S) = P(M) n P(M ^ S) = P(M) P(S) P(~M ^ S) = P(~M) P(S), P(M^~S) = P(M)P(~S), P(~M^~S) = P(~M)P(~S) n 16 三月 2018 Data Mining: Concepts and Techniques 90

Independence From P(S M) = P(S), the rules of probability imply: (can you prove these? ) And in general: n P(~S M) = P(~S) n P(M S) = P(M) n P(M ^ S) = P(M) P(S) P(M=u ^ S=v) = P(M=u) P(S=v) for each of the four combinations of u=True/False P(~M ^ S) = P(~M) P(S), (PM^~S) = P(M)P(~S), v=True/False P(~M^~S) = P(~M)P(~S) n 16 三月 2018 Data Mining: Concepts and Techniques 91

Independence We’ve stated: P(M) = 0. 6 From these statements, we can P(S) = 0. 3 P(S M) = P(S) derive the full joint pdf. S M T T T F F T F Prob F And since we now have the joint pdf, we can make any queries we like. 16 三月 2018 Data Mining: Concepts and Techniques 92

A more interesting case n n n M : Manuela teaches the class S : It is sunny L : The lecturer arrives slightly late. Assume both lecturers are sometimes delayed by bad weather. Andrew is more likely to arrive later than Manuela. 16 三月 2018 Data Mining: Concepts and Techniques 93

A more interesting case n n n M : Manuela teaches the class S : It is sunny L : The lecturer arrives slightly late. Assume both lecturers are sometimes delayed by bad weather. Andrew is more likely to arrive late than Manuela. Let’s begin with writing down knowledge we’re happy about: P(S M) = P(S), P(S) = 0. 3, P(M) = 0. 6 Lateness is not independent of the weather and is not independent of the lecturer. 16 三月 2018 Data Mining: Concepts and Techniques 94

A more interesting case n n n M : Manuela teaches the class S : It is sunny L : The lecturer arrives slightly late. Assume both lecturers are sometimes delayed by bad weather. Andrew is more likely to arrive late than Manuela. Let’s begin with writing down knowledge we’re happy about: P(S M) = P(S), P(S) = 0. 3, P(M) = 0. 6 Lateness is not independent of the weather and is not independent of the lecturer. We already know the Joint of S and M, so all we need now is P(L S=u, M=v) in the 4 cases of u/v = True/False. 16 三月 2018 Data Mining: Concepts and Techniques 95

A more interesting case n n n M : Manuela teaches the class S : It is sunny L : The lecturer arrives slightly late. Assume both lecturers are sometimes delayed by bad weather. Andrew is more likely to arrive late than Manuela. P(L M ^ S) = 0. 05 P(S M) = P(S) P(L M ^ ~S) = 0. 1 P(S) = 0. 3 P(L ~M ^ S) = 0. 1 P(M) = 0. 6 P(L ~M ^ ~S) = 0. 2 Now we can derive a full joint p. d. f. with a “mere” six numbers instead of seven* *Savings are larger for larger numbers of variables. 16 三月 2018 Data Mining: Concepts and Techniques 96

A more interesting case n n n M : Manuela teaches the class S : It is sunny L : The lecturer arrives slightly late. Assume both lecturers are sometimes delayed by bad weather. Andrew is more likely to arrive late than Manuela. P(L M ^ S) = 0. 05 P(S M) = P(S) P(L M ^ ~S) = 0. 1 P(S) = 0. 3 P(L ~M ^ S) = 0. 1 P(M) = 0. 6 P(L ~M ^ ~S) = 0. 2 Question: Express P(L=x ^ M=y ^ S=z) in terms that only need the above expressions, where x, y and z may each be True or False. 16 三月 2018 Data Mining: Concepts and Techniques 97
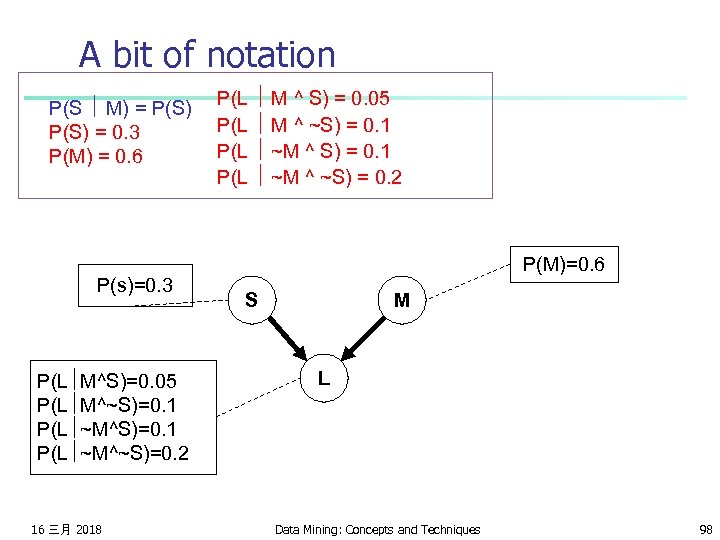
A bit of notation P(S M) = P(S) = 0. 3 P(M) = 0. 6 P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 16 三月 2018 P(L M ^ S) = 0. 05 P(L M ^ ~S) = 0. 1 P(L ~M ^ ~S) = 0. 2 P(M)=0. 6 S M L Data Mining: Concepts and Techniques 98
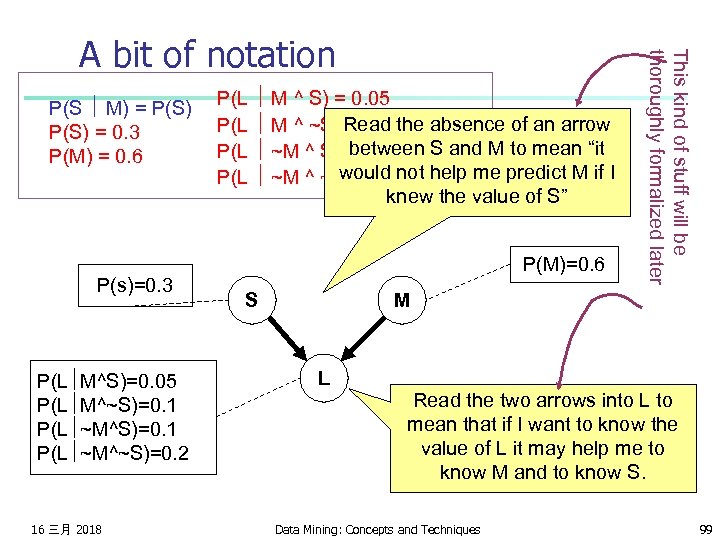
P(S M) = P(S) = 0. 3 P(M) = 0. 6 P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 16 三月 2018 P(L M ^ S) = 0. 05 P(L M ^ ~S) Read the absence of an arrow = 0. 1 between S and M to mean “it P(L ~M ^ S) = 0. 1 would not P(L ~M ^ ~S) = 0. 2 help me predict M if I knew the value of S” P(M)=0. 6 S This kind of stuff will be thoroughly formalized later A bit of notation M L Read the two arrows into L to mean that if I want to know the value of L it may help me to know M and to know S. Data Mining: Concepts and Techniques 99

An even cuter trick Suppose we have these three events: n M : Lecture taught by Manuela n L : Lecturer arrives late n R : Lecture concerns robots Suppose: n Andrew has a higher chance of being late than Manuela. n Andrew has a higher chance of giving robotics lectures. What kind of independence can we find? How about: P(L M) = P(L) ? n P(R M) = P(R) ? n P(L R) = P(L) ? n 16 三月 2018 Data Mining: Concepts and Techniques 100

Conditional independence Once you know who the lecturer is, then whether they arrive late doesn’t affect whether the lecture concerns robots. P(R M, L) = P(R M) and P(R ~M, L) = P(R ~M) We express this in the following way: “R and L are conditionally independent given M” . . which is also notated by the following diagram. 16 三月 2018 M L R Data Mining: Concepts and Techniques Given knowledge of M, knowing anything else in the diagram won’t help us with L, etc. 101

Conditional Independence formalized R and L are conditionally independent given M if for all x, y, z in {T, F}: P(R=x M=y ^ L=z) = P(R=x M=y) More generally: Let S 1 and S 2 and S 3 be sets of variables. Set-of-variables S 1 and set-of-variables S 2 are conditionally independent given S 3 if for all assignments of values to the variables in the sets, P(S 1’s assignments S 2’s assignments & S 3’s assignments)= P(S 1’s assignments S 3’s assignments) 16 三月 2018 Data Mining: Concepts and Techniques 102

Example: “Shoe-size is conditionally independent of Glove-size given height weight and age” means R and L are conditionally independent given M if forall s, g, h, w, a for all x, y, z in {T, F}: P(Shoe. Size=s|Height=h, Weight=w, Age=a) P(R=x M=y ^ L=z) = P(R=x M=y) = P(Shoe. Size=s|Height=h, Weight=w, Age=a, Glove. Size=g) More generally: Let S 1 and S 2 and S 3 be sets of variables. Set-of-variables S 1 and set-of-variables S 2 are conditionally independent given S 3 if for all assignments of values to the variables in the sets, P(S 1’s assignments S 2’s assignments & S 3’s assignments)= P(S 1’s assignments S 3’s assignments) 16 三月 2018 Data Mining: Concepts and Techniques 103

Example: “Shoe-size is conditionally independent of Glove-size given height weight and age” does not mean R and L are conditionally independent given M if forall s, g, h for all x, y, z in {T, F}: P(Shoe. Size=s|Height=h) P(R=x M=y ^ L=z) = P(R=x M=y) = P(Shoe. Size=s|Height=h, Glove. Size=g) More generally: Let S 1 and S 2 and S 3 be sets of variables. Set-of-variables S 1 and set-of-variables S 2 are conditionally independent given S 3 if for all assignments of values to the variables in the sets, P(S 1’s assignments S 2’s assignments & S 3’s assignments)= P(S 1’s assignments S 3’s assignments) 16 三月 2018 Data Mining: Concepts and Techniques 104

Conditional independence M L R We can write down P(M). And then, since we know L is only directly influenced by M, we can write down the values of P(L M) and P(L ~M) and know we’ve fully specified L’s behavior. Ditto for R. P(M) = 0. 6 ‘R and L conditionally P(L M) = 0. 085 independent given M’ P(L ~M) = 0. 17 P(R M) = 0. 3 P(R ~M) = 0. 6 16 三月 2018 Data Mining: Concepts and Techniques 105

Conditional independence M L R P(M) = 0. 6 P(L M) = 0. 085 P(L ~M) = 0. 17 P(R M) = 0. 3 P(R ~M) = 0. 6 Conditional Independence: P(R M, L) = P(R M), P(R ~M, L) = P(R ~M) Again, we can obtain any member of the Joint prob dist that we desire: P(L=x ^ R=y ^ M=z) = 16 三月 2018 Data Mining: Concepts and Techniques 106

Assume five variables T: The lecture started by 10: 35 L: The lecturer arrives late R: The lecture concerns robots M: The lecturer is Manuela S: It is sunny n n T only directly influenced by L (i. e. T is conditionally independent of R, M, S given L) L only directly influenced by M and S (i. e. L is conditionally independent of R given M & S) R only directly influenced by M (i. e. R is conditionally independent of L, S, given M) M and S are independent 16 三月 2018 Data Mining: Concepts and Techniques 107
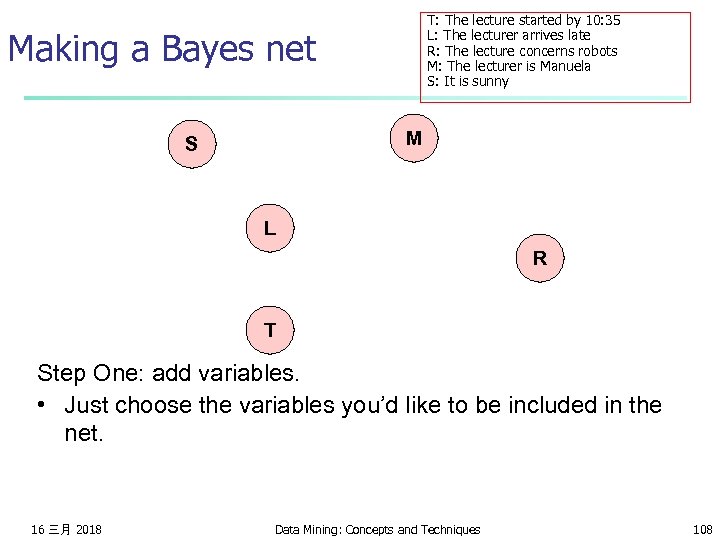
T: The lecture started by 10: 35 L: The lecturer arrives late R: The lecture concerns robots M: The lecturer is Manuela S: It is sunny Making a Bayes net M S L R T Step One: add variables. • Just choose the variables you’d like to be included in the net. 16 三月 2018 Data Mining: Concepts and Techniques 108
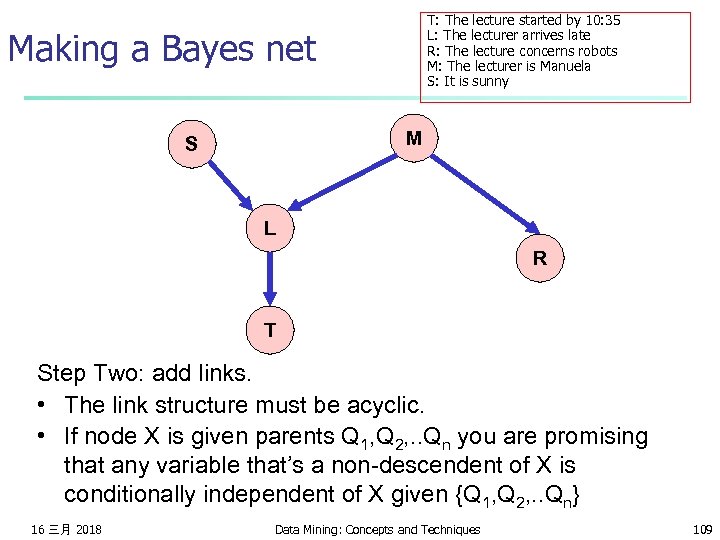
T: The lecture started by 10: 35 L: The lecturer arrives late R: The lecture concerns robots M: The lecturer is Manuela S: It is sunny Making a Bayes net M S L R T Step Two: add links. • The link structure must be acyclic. • If node X is given parents Q 1, Q 2, . . Qn you are promising that any variable that’s a non-descendent of X is conditionally independent of X given {Q 1, Q 2, . . Qn} 16 三月 2018 Data Mining: Concepts and Techniques 109
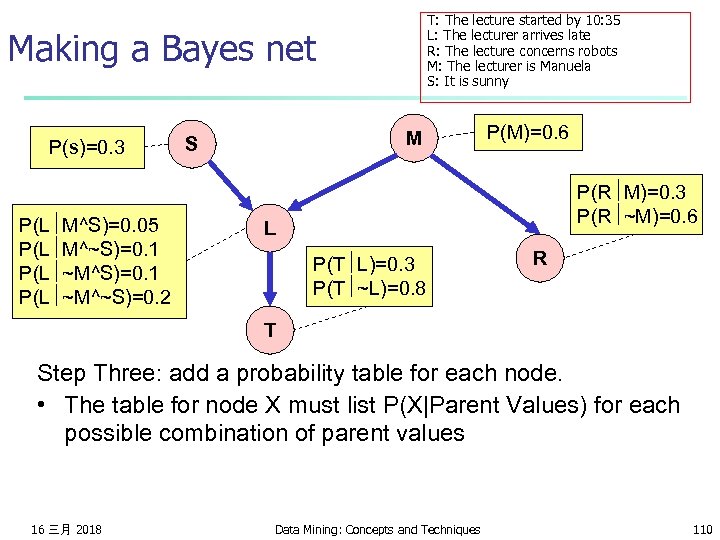
T: The lecture started by 10: 35 L: The lecturer arrives late R: The lecture concerns robots M: The lecturer is Manuela S: It is sunny Making a Bayes net P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T Step Three: add a probability table for each node. • The table for node X must list P(X|Parent Values) for each possible combination of parent values 16 三月 2018 Data Mining: Concepts and Techniques 110
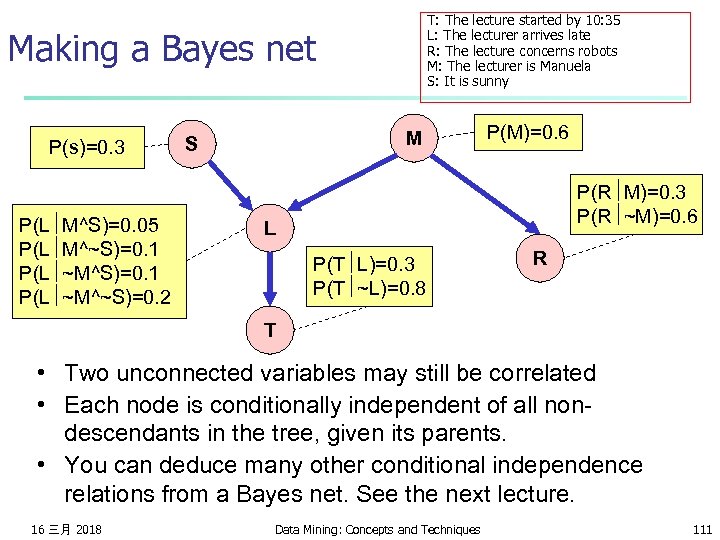
T: The lecture started by 10: 35 L: The lecturer arrives late R: The lecture concerns robots M: The lecturer is Manuela S: It is sunny Making a Bayes net P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T • Two unconnected variables may still be correlated • Each node is conditionally independent of all nondescendants in the tree, given its parents. • You can deduce many other conditional independence relations from a Bayes net. See the next lecture. 16 三月 2018 Data Mining: Concepts and Techniques 111

Bayes Nets Formalized A Bayes net (also called a belief network) is an augmented directed acyclic graph, represented by the pair V , E where: n n V is a set of vertices. E is a set of directed edges joining vertices. No loops of any length are allowed. Each vertex in V contains the following information: n n The name of a random variable A probability distribution table indicating how the probability of this variable’s values depends on all possible combinations of parental values. 16 三月 2018 Data Mining: Concepts and Techniques 112

Building a Bayes Net 1. 2. 3. 4. Choose a set of relevant variables. Choose an ordering for them Assume they’re called X 1. . Xm (where X 1 is the first in the ordering, X 1 is the second, etc) For i = 1 to m: 1. 2. 3. 16 三月 2018 Add the Xi node to the network Set Parents(Xi ) to be a minimal subset of {X 1…Xi-1} such that we have conditional independence of Xi and all other members of {X 1…Xi-1} given Parents(Xi ) Define the probability table of P(Xi =k Assignments of Parents(Xi ) ). Data Mining: Concepts and Techniques 113
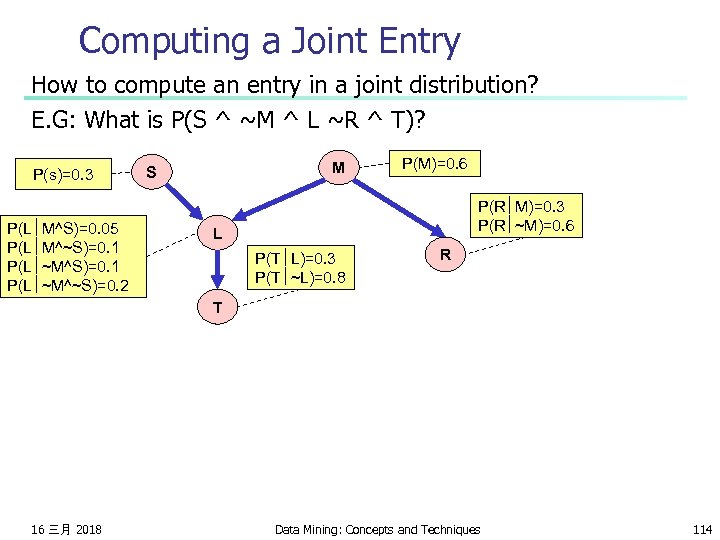
Computing a Joint Entry How to compute an entry in a joint distribution? E. G: What is P(S ^ ~M ^ L ~R ^ T)? P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T 16 三月 2018 Data Mining: Concepts and Techniques 114
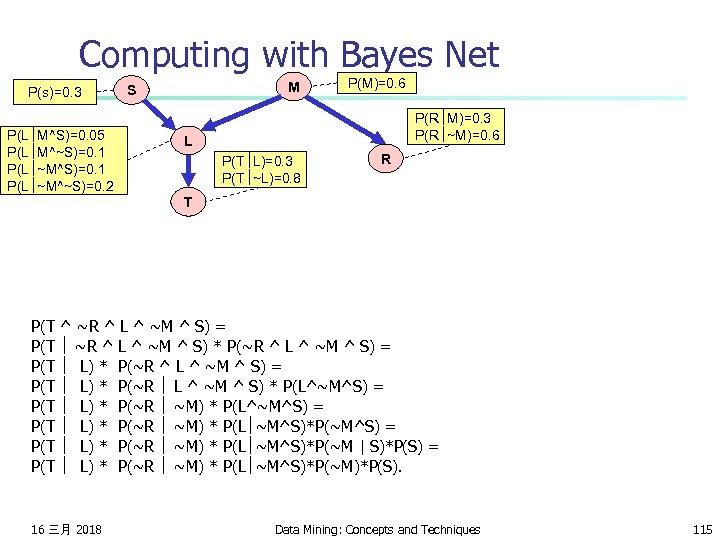
Computing with Bayes Net P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T P(T ^ ~R ^ L ^ ~M ^ S) = P(T ~R ^ L ^ ~M ^ S) * P(~R ^ L ^ ~M ^ S) = P(T L) * P(~R L ^ ~M ^ S) * P(L^~M^S) = P(T L) * P(~R ~M) * P(L ~M^S)*P(~M^S) = P(T L) * P(~R ~M) * P(L ~M^S)*P(~M | S)*P(S) = P(T L) * P(~R ~M) * P(L ~M^S)*P(~M)*P(S). 16 三月 2018 Data Mining: Concepts and Techniques 115

The general case P(X 1=x 1 ^ X 2=x 2 ^ …. Xn-1=xn-1 ^ Xn=xn) = P(Xn=xn ^ Xn-1=xn-1 ^ …. X 2=x 2 ^ X 1=x 1) = P(Xn=xn Xn-1=xn-1 ^ …. X 2=x 2 ^ X 1=x 1) * P(Xn-1=xn-1 ^…. X 2=x 2 ^ X 1=x 1) = P(Xn=xn Xn-1=xn-1 ^ …. X 2=x 2 ^ X 1=x 1) * P(Xn-1=xn-1 …. X 2=x 2 ^ X 1=x 1) * P(Xn-2=xn-2 ^…. X 2=x 2 ^ X 1=x 1) = : : = So any entry in joint pdf table can be computed. And so any conditional probability can be computed. 16 三月 2018 Data Mining: Concepts and Techniques 116
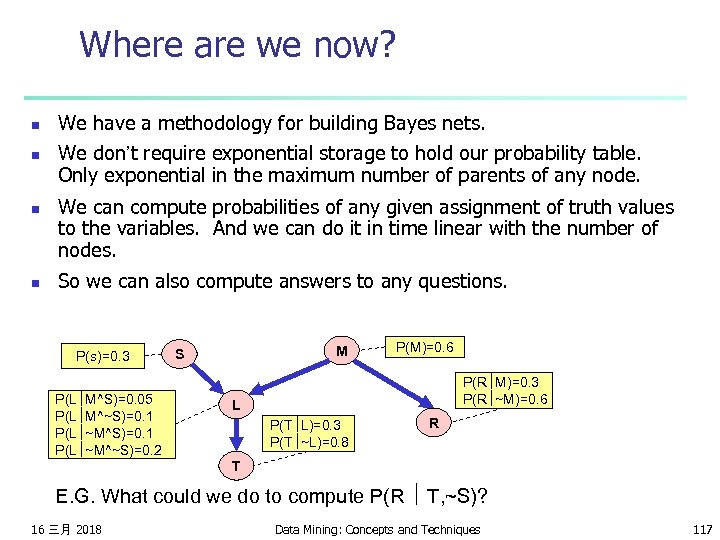
Where are we now? n n We have a methodology for building Bayes nets. We don’t require exponential storage to hold our probability table. Only exponential in the maximum number of parents of any node. We can compute probabilities of any given assignment of truth values to the variables. And we can do it in time linear with the number of nodes. So we can also compute answers to any questions. P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T E. G. What could we do to compute P(R T, ~S)? 16 三月 2018 Data Mining: Concepts and Techniques 117
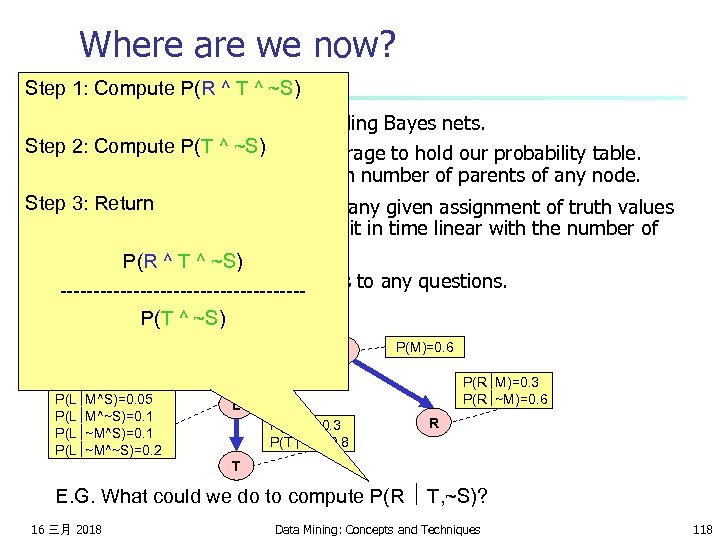
Where are we now? Step 1: Compute P(R ^ T ^ ~S) We have a methodology for building Bayes nets. Step 2: Compute P(T ^ ~S) n We don’t require exponential storage to hold our probability table. Only exponential in the maximum number of parents of any node. Step 3: Return n We can compute probabilities of any given assignment of truth values to the variables. And we can do it in time linear with the number of nodes. P(R ^ T ^ ~S) n So we can also compute answers to any questions. ------------------P(T ^ ~S) n P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T E. G. What could we do to compute P(R T, ~S)? 16 三月 2018 Data Mining: Concepts and Techniques 118
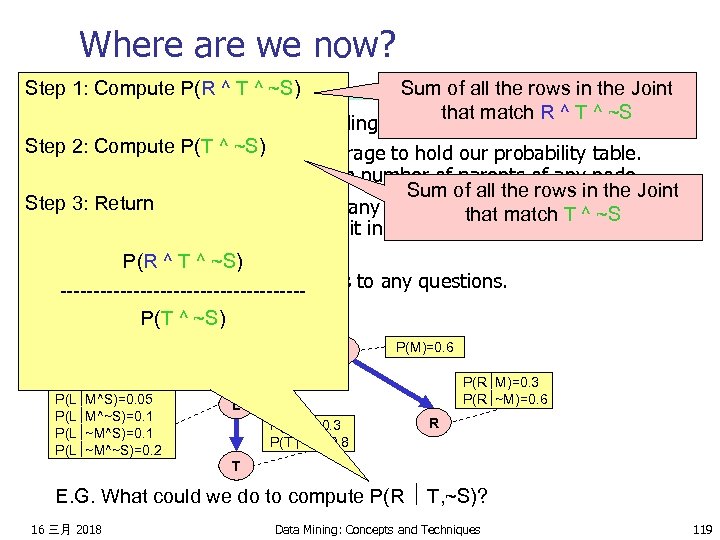
Where are we now? Sum of all the rows in the Joint that match R ^ T ^ ~S n We have a methodology for building Bayes nets. Step 2: Compute P(T ^ ~S) n We don’t require exponential storage to hold our probability table. Only exponential in the maximum number of parents of any node. Sum of all the rows in the Joint Step 3: Return n We can compute probabilities of any given assignment of truth values that match T ^ ~S to the variables. And we can do it in time linear with the number of nodes. P(R ^ T ^ ~S) n So we can also compute answers to any questions. ------------------P(T ^ ~S) Step 1: Compute P(R ^ T ^ ~S) P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T E. G. What could we do to compute P(R T, ~S)? 16 三月 2018 Data Mining: Concepts and Techniques 119
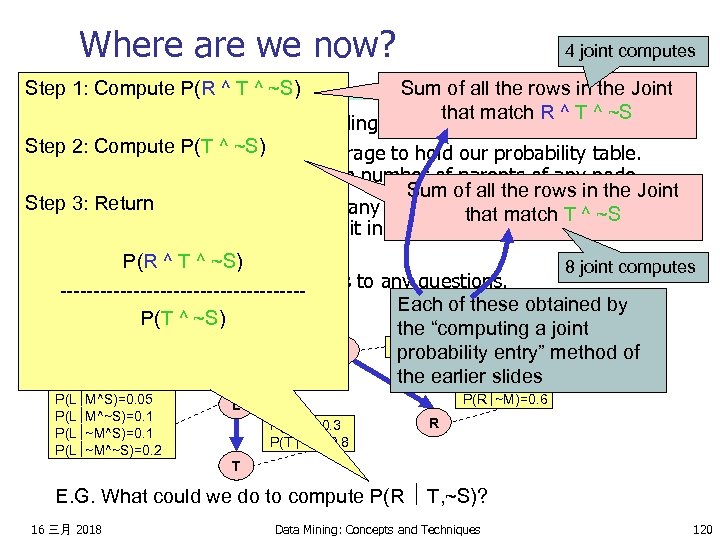
Where are we now? 4 joint computes Sum of all the rows in the Joint that match R ^ T ^ ~S n We have a methodology for building Bayes nets. Step 2: Compute P(T ^ ~S) n We don’t require exponential storage to hold our probability table. Only exponential in the maximum number of parents of any node. Sum of all the rows in the Joint Step 3: Return n We can compute probabilities of any given assignment of truth values that match T ^ ~S to the variables. And we can do it in time linear with the number of nodes. P(R ^ T ^ ~S) 8 joint computes n So we can also compute answers to any questions. ------------------Each of these obtained by P(T ^ ~S) the “computing a joint Step 1: Compute P(R ^ T ^ ~S) P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 probability entry” method of the earlier slides P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T E. G. What could we do to compute P(R T, ~S)? 16 三月 2018 Data Mining: Concepts and Techniques 120

The good news We can do inference. We can compute any conditional probability: P( Some variable Some other variable values ) 16 三月 2018 Data Mining: Concepts and Techniques 121

The good news We can do inference. We can compute any conditional probability: P( Some variable Some other variable values ) Suppose you have m binary-valued variables in your Bayes Net and expression E 2 mentions k variables. How much work is the above computation? 16 三月 2018 Data Mining: Concepts and Techniques 122

The sad, bad news Conditional probabilities by enumerating all matching entries in the joint are expensive: Exponential in the number of variables. 16 三月 2018 Data Mining: Concepts and Techniques 123

The sad, bad news Conditional probabilities by enumerating all matching entries in the joint are expensive: Exponential in the number of variables. But perhaps there are faster ways of querying Bayes nets? n In fact, if I ever ask you to manually do a Bayes Net inference, you’ll find there are often many tricks to save you time. n So we’ve just got to program our computer to do those tricks too, right? 16 三月 2018 Data Mining: Concepts and Techniques 124

The sad, bad news Conditional probabilities by enumerating all matching entries in the joint are expensive: Exponential in the number of variables. But perhaps there are faster ways of querying Bayes nets? n In fact, if I ever ask you to manually do a Bayes Net inference, you’ll find there are often many tricks to save you time. n So we’ve just got to program our computer to do those tricks too, right? Sadder and worse news: General querying of Bayes nets is NP-complete. 16 三月 2018 Data Mining: Concepts and Techniques 125
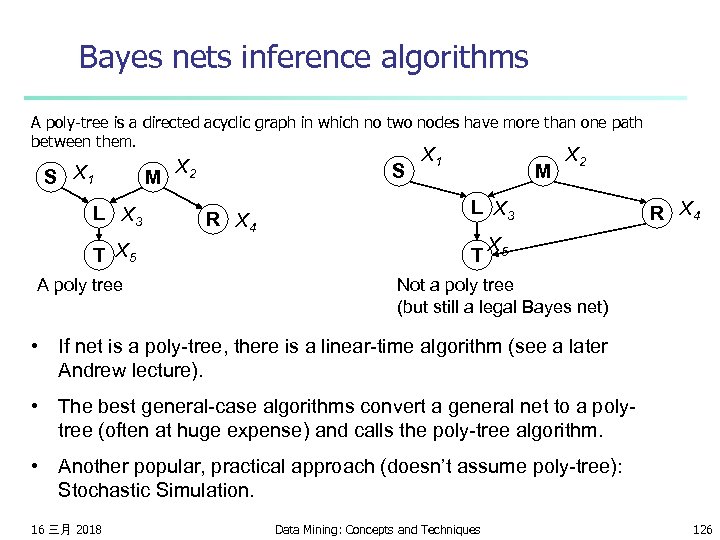
Bayes nets inference algorithms A poly-tree is a directed acyclic graph in which no two nodes have more than one path between them. S X 1 L X 3 T X 5 A poly tree M X 2 S R X 4 X 1 M X 2 L X 3 T R X 4 X 5 Not a poly tree (but still a legal Bayes net) • If net is a poly-tree, there is a linear-time algorithm (see a later Andrew lecture). • The best general-case algorithms convert a general net to a polytree (often at huge expense) and calls the poly-tree algorithm. • Another popular, practical approach (doesn’t assume poly-tree): Stochastic Simulation. 16 三月 2018 Data Mining: Concepts and Techniques 126
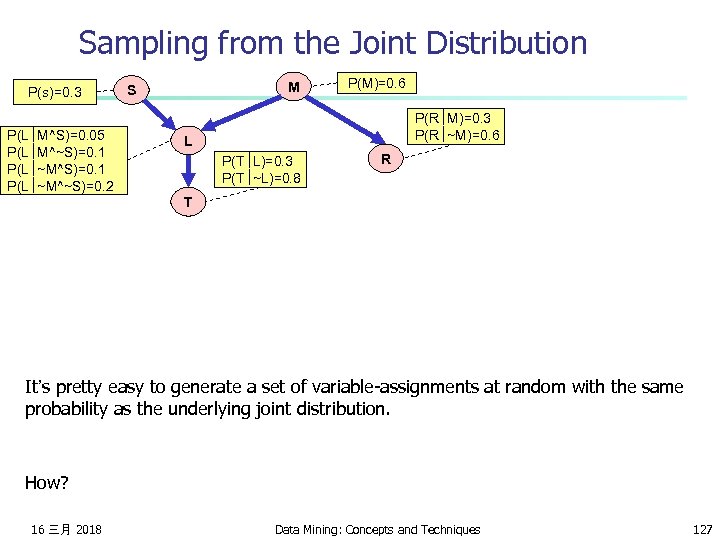
Sampling from the Joint Distribution P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T It’s pretty easy to generate a set of variable-assignments at random with the same probability as the underlying joint distribution. How? 16 三月 2018 Data Mining: Concepts and Techniques 127
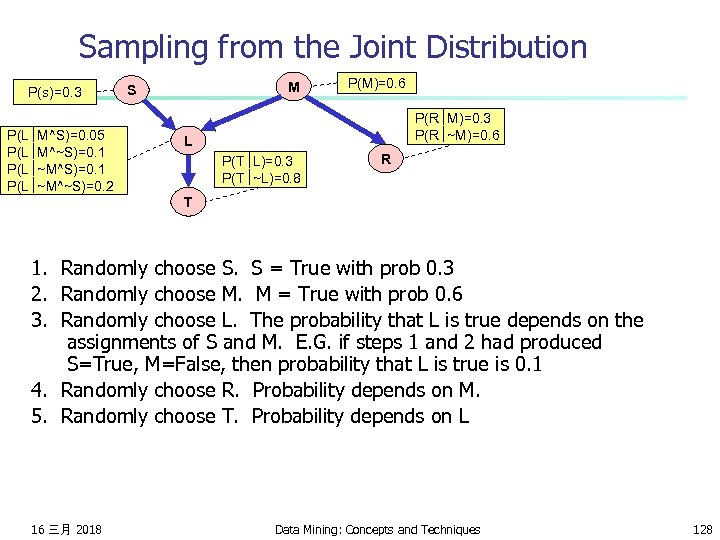
Sampling from the Joint Distribution P(s)=0. 3 P(L M^S)=0. 05 P(L M^~S)=0. 1 P(L ~M^~S)=0. 2 M S P(M)=0. 6 P(R M)=0. 3 P(R ~M)=0. 6 L P(T L)=0. 3 P(T ~L)=0. 8 R T 1. Randomly choose S. S = True with prob 0. 3 2. Randomly choose M. M = True with prob 0. 6 3. Randomly choose L. The probability that L is true depends on the assignments of S and M. E. G. if steps 1 and 2 had produced S=True, M=False, then probability that L is true is 0. 1 4. Randomly choose R. Probability depends on M. 5. Randomly choose T. Probability depends on L 16 三月 2018 Data Mining: Concepts and Techniques 128

A general sampling algorithm Let’s generalize the example on the previous slide to a general Bayes Net. As in Slides 16 -17 , call the variables X 1. . Xn, where Parents(Xi) must be a subset of {X 1. . Xi-1}. For i=1 to n: 1. Find parents, if any, of Xi. Assume n(i) parents. Call them Xp(i, 1), Xp(i, 2), …Xp(i, n(i)). 2. Recall the values that those parents were randomly given: xp(i, 1), xp(i, 2), …xp(i, n(i)). 3. Look up in the lookup-table for: P(Xi=True Xp(i, 1)=xp(i, 1), Xp(i, 2)=xp(i, 2)…Xp(i, n(i))=xp(i, n(i))) 4. Randomly set xi=True according to this probability x 1, x 2, …xn are now a sample from the joint distribution of X 1, X 2, …Xn. 16 三月 2018 Data Mining: Concepts and Techniques 129

Stochastic Simulation Example Someone wants to know P(R = True T = True ^ S = False ) We’ll do lots of random samplings and count the number of occurrences of the following: n n n Nc : Num. samples in which T=True and S=False. Ns : Num. samples in which R=True, T=True and S=False. N : Number of random samplings Now if N is big enough: Nc /N is a good estimate of P(T=True and S=False). Ns /N is a good estimate of P(R=True , T=True , S=False). P(R T^~S) = P(R^T^~S)/P(T^~S), so Ns / Nc can be a good estimate of P(R T^~S). 16 三月 2018 Data Mining: Concepts and Techniques 130

General Stochastic Simulation Someone wants to know P(E 1 E 2 ) We’ll do lots of random samplings and count the number of occurrences of the following: n n n Nc : Num. samples in which E 2 Ns : Num. samples in which E 1 and E 2 N : Number of random samplings Now if N is big enough: Nc /N is a good estimate of P(E 2). Ns /N is a good estimate of P(E 1 , E 2). P(E 1 E 2) = P(E 1^ E 2)/P(E 2), so Ns / Nc can be a good estimate of P(E 1 E 2). 16 三月 2018 Data Mining: Concepts and Techniques 131

Likelihood weighting Problem with Stochastic Sampling: With lots of constraints in E, or unlikely events in E, then most of the simulations will be thrown away, (they’ll have no effect on Nc, or Ns). Imagine we’re part way through our simulation. In E 2 we have the constraint Xi = v We’re just about to generate a value for Xi at random. Given the values assigned to the parents, we see that P(Xi = v parents) = p. Now we know that with stochastic sampling: we’ll generate “Xi = v” proportion p of the time, and proceed. n And we’ll generate a different value proportion 1 -p of the time, and the simulation will be wasted. n Instead, always generate Xi = v, but weight the answer by weight “p” to compensate. 16 三月 2018 Data Mining: Concepts and Techniques 132

Likelihood weighting Set Nc : =0, Ns : =0 1. Generate a random assignment of all variables that matches E 2. This process returns a weight w. 2. Define w to be the probability that this assignment would have been generated instead of an unmatching assignment during its generation in the original algorithm. Fact: w is a product of all likelihood factors involved in the generation. 3. Nc : = Nc + w If our sample matches E 1 then Ns : = Ns + w 5. Go to 1 Again, Ns / Nc estimates P(E 1 E 2 ) 4. 16 三月 2018 Data Mining: Concepts and Techniques 133

Case Study I Pathfinder system. (Heckerman 1991, Probabilistic Similarity Networks, MIT Press, Cambridge MA). n Diagnostic system for lymph-node diseases. n 60 diseases and 100 symptoms and test-results. n 14, 000 probabilities n Expert consulted to make net. n n n 35 hours for net topology. n n 8 hours to determine variables. 40 hours for probability table values. Apparently, the experts found it quite easy to invent the causal links and probabilities. Pathfinder is now outperforming the world experts in diagnosis. Being extended to several dozen other medical domains. 16 三月 2018 Data Mining: Concepts and Techniques 134

Questions n n n What are the strengths of probabilistic networks compared with propositional logic? What are the weaknesses of probabilistic networks compared with propositional logic? What are the strengths of probabilistic networks compared with predicate logic? What are the weaknesses of probabilistic networks compared with predicate logic? (How) could predicate logic and probabilistic networks be combined? 16 三月 2018 Data Mining: Concepts and Techniques 135

What you should know n n n The meanings and importance of independence and conditional independence. The definition of a Bayes net. Computing probabilities of assignments of variables (i. e. members of the joint p. d. f. ) with a Bayes net. The slow (exponential) method for computing arbitrary, conditional probabilities. The stochastic simulation method and likelihood weighting. 16 三月 2018 Data Mining: Concepts and Techniques 136

Content n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) 16 三月 2018 Data Mining: Concepts and Techniques 137

Neural Networks n Assume each record X is a vector of length n. n There are two classes which are valued 1 and -1. E. g. class 1 means “buy computer”, and class -1 means “no buy”. n We can incrementally change weights to learn to produce these outputs using the perceptron learning rule. 16 三月 2018 Data Mining: Concepts and Techniques 138
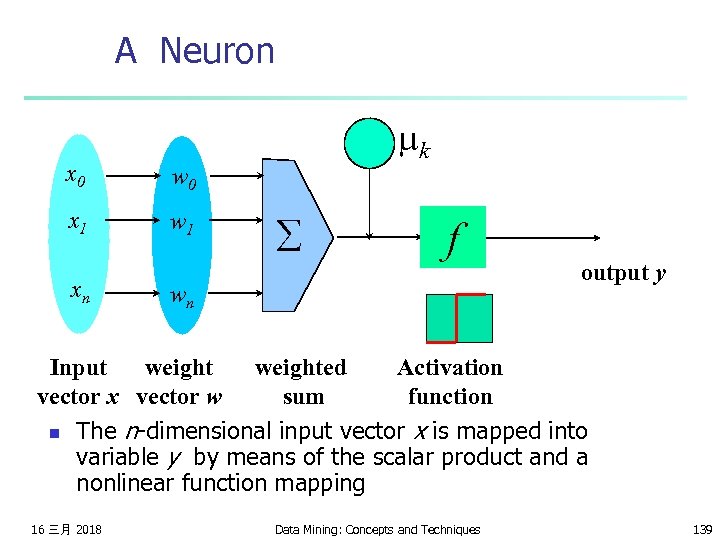
A Neuron x 0 w 0 x 1 w 1 - mk xn å f wn output y Input weighted Activation vector x vector w sum function n The n-dimensional input vector x is mapped into variable y by means of the scalar product and a nonlinear function mapping 16 三月 2018 Data Mining: Concepts and Techniques 139
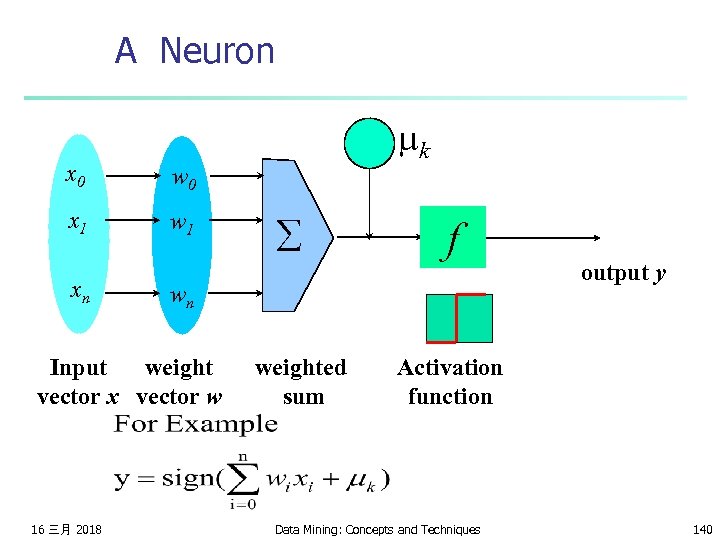
A Neuron x 0 w 0 x 1 w 1 - mk xn f wn Input weight vector x vector w 16 三月 2018 å weighted sum output y Activation function Data Mining: Concepts and Techniques 140
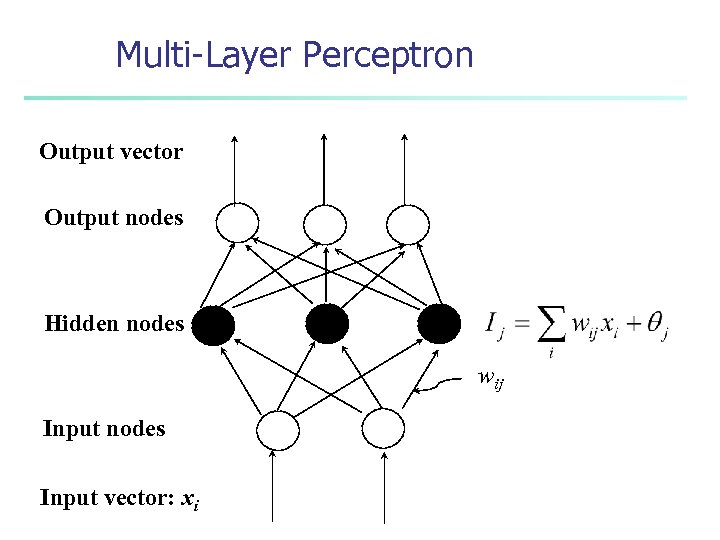
Multi-Layer Perceptron Output vector Output nodes Hidden nodes wij Input nodes Input vector: xi

Network Training n n The ultimate objective of training n obtain a set of weights that makes almost all the tuples in the training data classified correctly Steps n Initialize weights with random values n Feed the input tuples into the network one by one n For each unit n n Compute the net input to the unit as a linear combination of all the inputs to the unit Compute the output value using the activation function Compute the error Update the weights and the bias

Content n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) 16 三月 2018 Data Mining: Concepts and Techniques 144

Linear Support Vector Machines Margin n n Goal: find a plane that divides the two sets of points. Also, need to maximize margin. value( )= -1, e. g. does not buy computer value( )= 1, e. g. buy computer
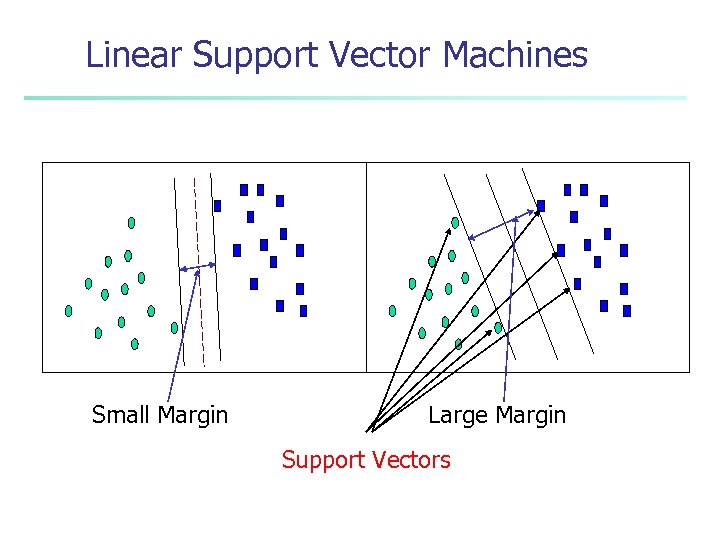
Linear Support Vector Machines Small Margin Large Margin Support Vectors

Linear Support Vector Machines n n + w·x 1 -1 b= b= + w·x The hyperplane is defined by vector w and value b. For any point x where value(x)=-1, w·x +b ≤ -1. For any point x where value(x)=1, w·x +b ≥ 1. Here let x = (xh , xv) w=(wh , wv), we have: w·x = wh xh + wv xv
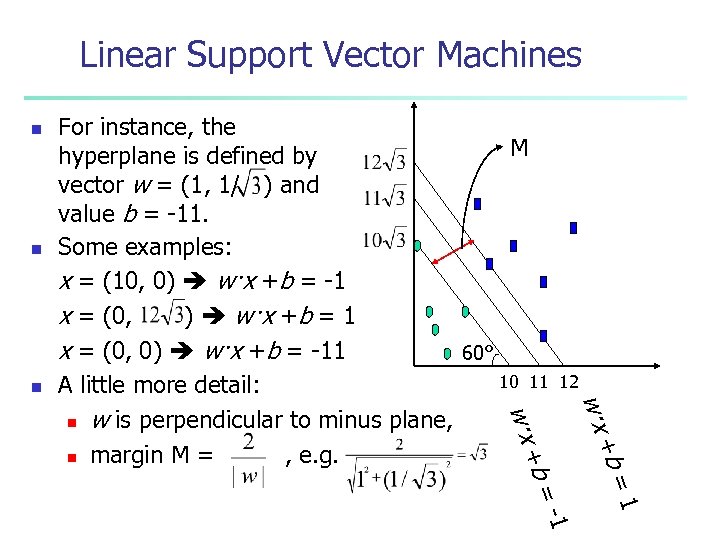
Linear Support Vector Machines n n n 12 + w·x 1 -1 b= b= + w·x For instance, the M hyperplane is defined by vector w = (1, 1/ ) and value b = -11. Some examples: x = (10, 0) w·x +b = -1 x = (0, ) w·x +b = 1 x = (0, 0) w·x +b = -11 60° 10 11 A little more detail: n w is perpendicular to minus plane, n margin M = , e. g.

Linear Support Vector Machines n n Each record xi in training data has a vector and a class, n There are two classes: 1 and -1, n E. g. class 1 = “buy computer”, class -1 = “not buy”. n E. g. a record (age, salary) = (45, 50 k), class = 1. Read the training data, find the hyperplane defined by w and b. Should maximize margin, minimize error. Can be done by Quadratic Programming Technique. Predict the class of a new data x by looking at the sign of w·x +b. Positive: class 1. Negative: class -1.
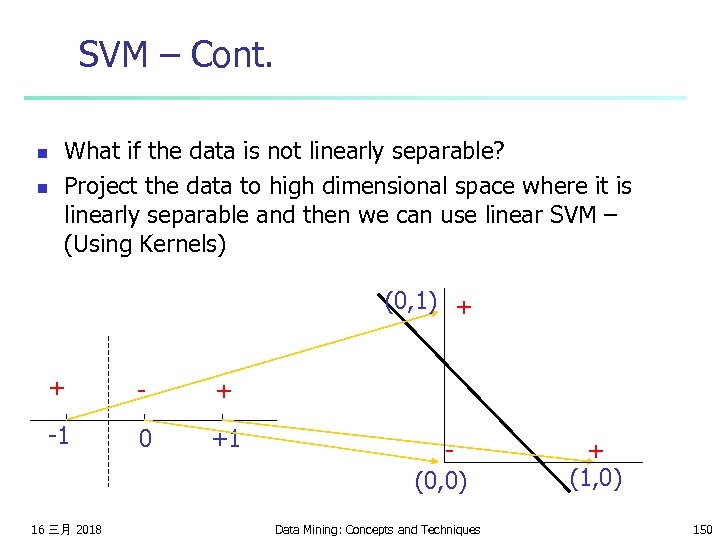
SVM – Cont. n n What if the data is not linearly separable? Project the data to high dimensional space where it is linearly separable and then we can use linear SVM – (Using Kernels) (0, 1) + + -1 0 +1 16 三月 2018 (0, 0) Data Mining: Concepts and Techniques + (1, 0) 150

Non-Linear SVM Classification using SVM (w, b) In non linear case we can see this as Kernel – Can be thought of as doing dot product in some high dimensional space 16 三月 2018 Data Mining: Concepts and Techniques 151
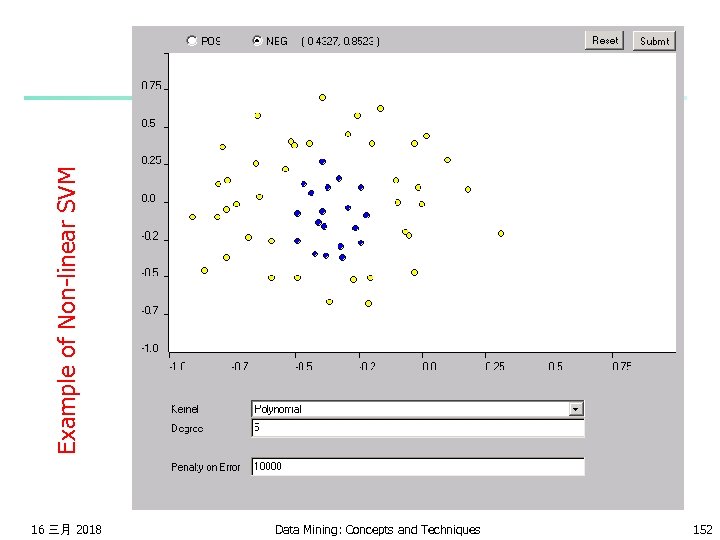
Example of Non-linear SVM 16 三月 2018 Data Mining: Concepts and Techniques 152
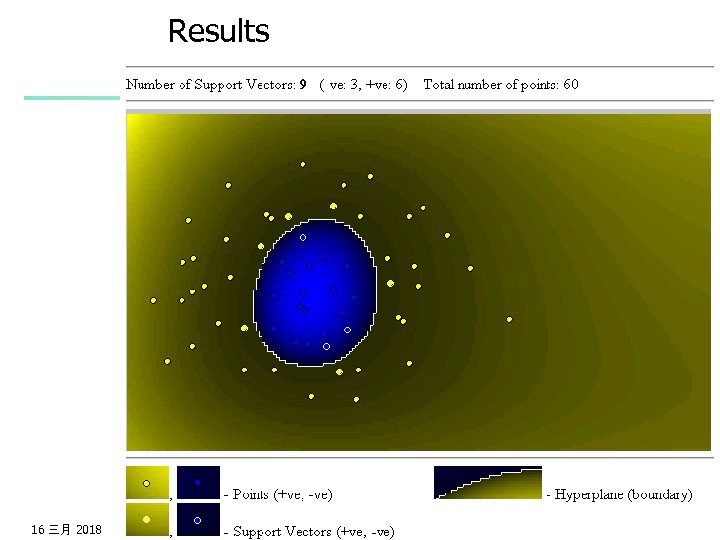
Results 16 三月 2018 Data Mining: Concepts and Techniques 153

SVM vs. Neural Network n SVM n Relatively new concept n Nice Generalization properties n Hard to learn – learned in batch mode using quadratic programming techniques n Using kernels can learn very complex functions 16 三月 2018 n Neural Network n Quite Old n Generalizes well but doesn’t have strong mathematical foundation n Can easily be learned in incremental fashion n To learn complex functions – use multilayer perceptron (not that trivial) Data Mining: Concepts and Techniques 154

SVM Related Links n http: //svm. dcs. rhbnc. ac. uk/ n http: //www. kernel-machines. org/ n n n C. J. C. Burges. A Tutorial on Support Vector Machines for Pattern Recognition. Knowledge Discovery and Data Mining, 2(2), 1998. SVMlight – Software (in C) http: //ais. gmd. de/~thorsten/svm_light BOOK: An Introduction to Support Vector Machines N. Cristianini and J. Shawe-Taylor Cambridge University Press 16 三月 2018 Data Mining: Concepts and Techniques 155

Content n n n n What is classification? Decision tree Naïve Bayesian Classifier Baysian Networks Neural Networks Support Vector Machines (SVM) Bagging and Boosting 16 三月 2018 Data Mining: Concepts and Techniques 156
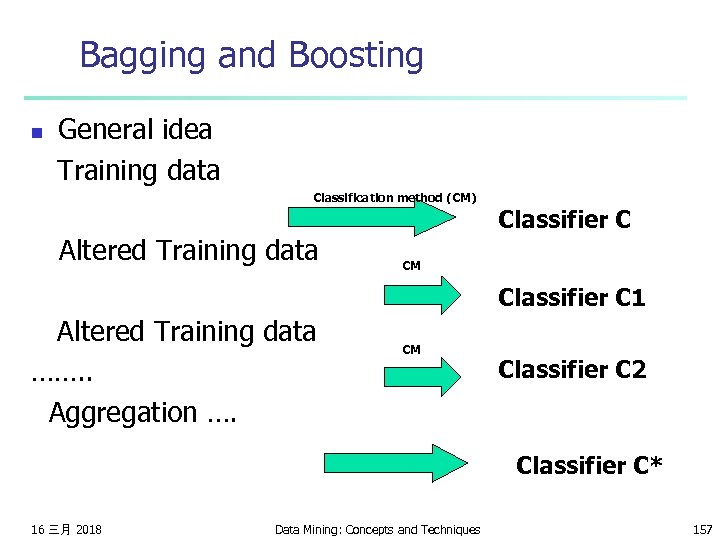
Bagging and Boosting General idea Training data n Classification method (CM) Altered Training data Classifier C CM Classifier C 1 Altered Training data ……. . Aggregation …. CM Classifier C 2 Classifier C* 16 三月 2018 Data Mining: Concepts and Techniques 157

Bagging n n n Given a set S of s samples Generate a bootstrap sample T from S. Cases in S may not appear in T or may appear more than once. Repeat this sampling procedure, getting a sequence of k independent training sets A corresponding sequence of classifiers C 1, C 2, …, Ck is constructed for each of these training sets, by using the same classification algorithm To classify an unknown sample X, let each classifier predict or vote The Bagged Classifier C* counts the votes and assigns X to the class with the “most” votes 16 三月 2018 Data Mining: Concepts and Techniques 158

Boosting Technique — Algorithm n Assign every example an equal weight 1/N n For t = 1, 2, …, T Do Obtain a hypothesis (classifier) h(t) under w(t) n Calculate the error of h(t) and re-weight the examples based on the error. Each classifier is dependent on the previous ones. Samples that are incorrectly predicted are weighted more heavily (t+1) to sum to 1 (weights assigned to n Normalize w different classifiers sum to 1) Output a weighted sum of all the hypothesis, with each hypothesis weighted according to its accuracy on the training set n n 16 三月 2018 Data Mining: Concepts and Techniques 159

Summary n Classification is an extensively studied problem (mainly in statistics, machine learning & neural networks) n Classification is probably one of the most widely used data mining techniques with a lot of extensions n Scalability is still an important issue for database applications: thus combining classification with database techniques should be a promising topic n Research directions: classification of non-relational data, e. g. , text, spatial, multimedia, etc. . 16 三月 2018 Data Mining: Concepts and Techniques 160
3e85f20112215490f91a651e353233dd.ppt