BF1_CFall2011_RR.ppt
- Количество слайдов: 63
 Class Risk and Return Historical returns in the USA. Sigma. CV. Security Characteristic Line (SCL). Beta. Security Market Line (SML). CAPM formula. Security Market Line (SML). Study materials: KR: Ch. 11, 12. RWJ: Ch. 9, 10 BM: Ch. 7, 8 WIUU BF 1, v. 4/2010, A. Zaporozhetz 1
Class Risk and Return Historical returns in the USA. Sigma. CV. Security Characteristic Line (SCL). Beta. Security Market Line (SML). CAPM formula. Security Market Line (SML). Study materials: KR: Ch. 11, 12. RWJ: Ch. 9, 10 BM: Ch. 7, 8 WIUU BF 1, v. 4/2010, A. Zaporozhetz 1
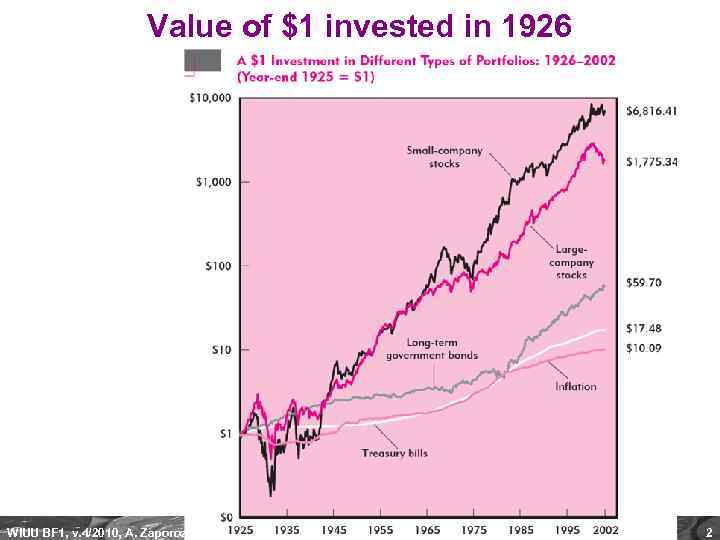 Value of $1 invested in 1926 WIUU BF 1, v. 4/2010, A. Zaporozhetz 2
Value of $1 invested in 1926 WIUU BF 1, v. 4/2010, A. Zaporozhetz 2
 Risk and Return Risk - The chance that an investment's actual return will be different than expected. This includes the possibility of losing some or all of the original investment. Total risk measured by the standard deviation of the historical returns. A fundamental idea in finance is the relationship between risk and return. The greater the amount of risk that an investor is willing to take on, the greater the potential return. The reason for this is that investors need to be compensated for taking on additional risk. E. g. , a U. S. Treasury bonds (bills) is considered to be the safest investment and, when compared to a corporate bond, provides a lower return. The reason is that a corporation is much more likely to go bankrupt than the U. S. government. WIUU BF 1, v. 4/2010, A. Zaporozhetz 3
Risk and Return Risk - The chance that an investment's actual return will be different than expected. This includes the possibility of losing some or all of the original investment. Total risk measured by the standard deviation of the historical returns. A fundamental idea in finance is the relationship between risk and return. The greater the amount of risk that an investor is willing to take on, the greater the potential return. The reason for this is that investors need to be compensated for taking on additional risk. E. g. , a U. S. Treasury bonds (bills) is considered to be the safest investment and, when compared to a corporate bond, provides a lower return. The reason is that a corporation is much more likely to go bankrupt than the U. S. government. WIUU BF 1, v. 4/2010, A. Zaporozhetz 3
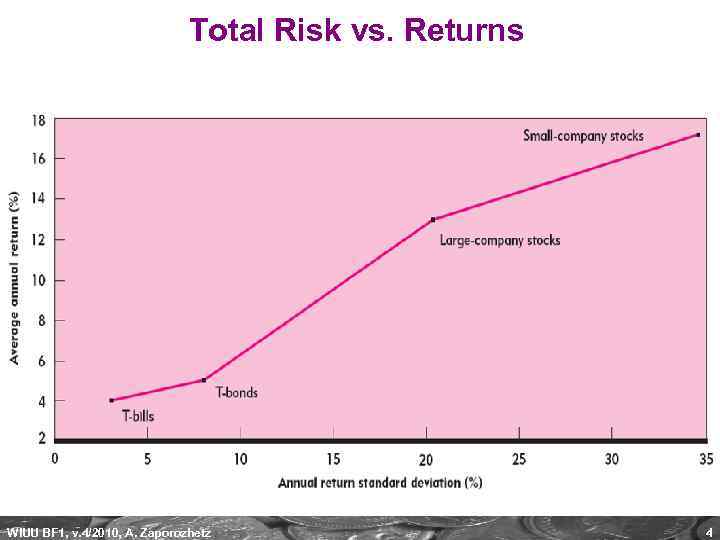 Total Risk vs. Returns WIUU BF 1, v. 4/2010, A. Zaporozhetz 4
Total Risk vs. Returns WIUU BF 1, v. 4/2010, A. Zaporozhetz 4
 Risk and Return, % = P 1 / P 0 - 1 P 1 – P 0 (+ ∑D) HPR, % = P 0 CV = sigma / mean return WIUU BF 1, v. 4/2010, A. Zaporozhetz 5
Risk and Return, % = P 1 / P 0 - 1 P 1 – P 0 (+ ∑D) HPR, % = P 0 CV = sigma / mean return WIUU BF 1, v. 4/2010, A. Zaporozhetz 5
 Measuring Returns Historical returns: X 1=10%, X 2= (-5%), X 3 = 20% Arithmetic Average: [0. 10 + (-0. 05) + 0. 20] / 3 = 8. 33% - usual way Geometric Average: [(1. 10)*(0. 95)*(1. 20)]1/3 - 1 = 7. 84% - more correct WIUU BF 1, v. 4/2010, A. Zaporozhetz 6
Measuring Returns Historical returns: X 1=10%, X 2= (-5%), X 3 = 20% Arithmetic Average: [0. 10 + (-0. 05) + 0. 20] / 3 = 8. 33% - usual way Geometric Average: [(1. 10)*(0. 95)*(1. 20)]1/3 - 1 = 7. 84% - more correct WIUU BF 1, v. 4/2010, A. Zaporozhetz 6
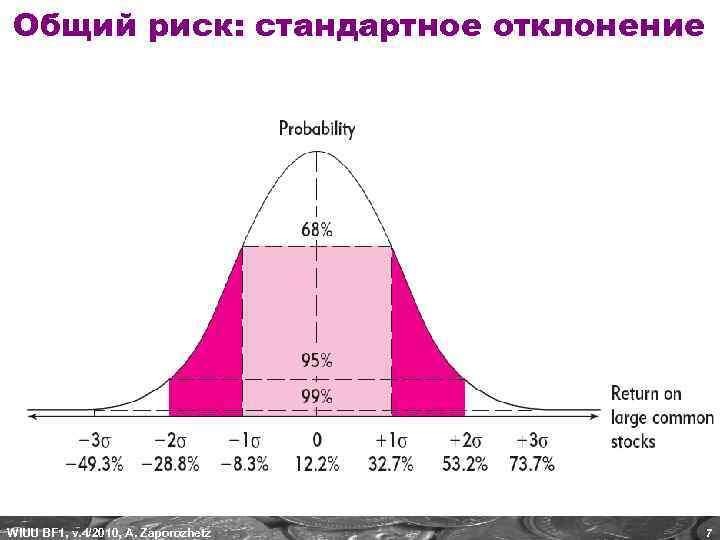 Общий риск: стандартное отклонение WIUU BF 1, v. 4/2010, A. Zaporozhetz 7
Общий риск: стандартное отклонение WIUU BF 1, v. 4/2010, A. Zaporozhetz 7
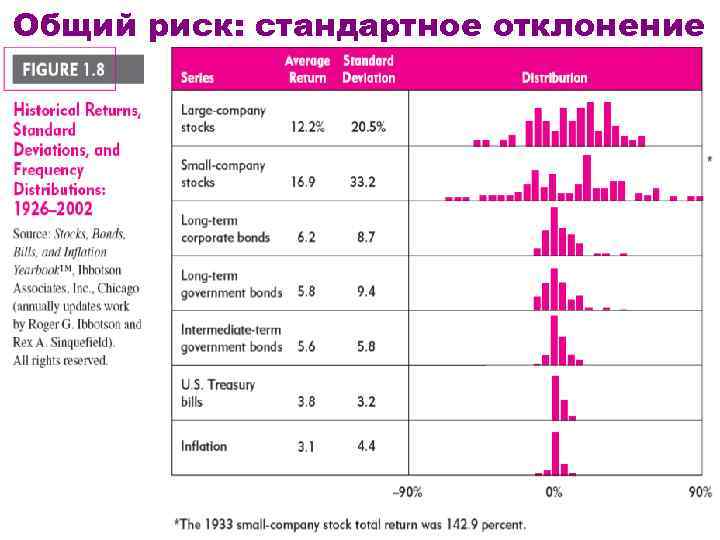 Общий риск: стандартное отклонение 2. Risk and return relationship WIUU BF 1, v. 4/2010, A. Zaporozhetz 8
Общий риск: стандартное отклонение 2. Risk and return relationship WIUU BF 1, v. 4/2010, A. Zaporozhetz 8
 Risk and Return measures Return (actual), mean return, % CAPM-return (model return), % Risk-free return, % Excess return, % Abnormal return, % Total risk (sigma), % Systematic risk (beta), t Unsystematic risk, % Coefficient of correlation, t Coefficient of determination, t Coefficient of variation (CV), t Sharpe’s measure (S), t Treynor’s measure (T), t Appraisal ratio (AR), t Z-beta, t Z-alpha, % Degree of volatility, t WIUU BF 1, v. 4/2010, A. Zaporozhetz 9
Risk and Return measures Return (actual), mean return, % CAPM-return (model return), % Risk-free return, % Excess return, % Abnormal return, % Total risk (sigma), % Systematic risk (beta), t Unsystematic risk, % Coefficient of correlation, t Coefficient of determination, t Coefficient of variation (CV), t Sharpe’s measure (S), t Treynor’s measure (T), t Appraisal ratio (AR), t Z-beta, t Z-alpha, % Degree of volatility, t WIUU BF 1, v. 4/2010, A. Zaporozhetz 9
 Measuring Risk: ERR Expected return: The return for an asset is the probability weighted average return in all scenarios. WIUU BF 1, v. 4/2010, A. Zaporozhetz 10
Measuring Risk: ERR Expected return: The return for an asset is the probability weighted average return in all scenarios. WIUU BF 1, v. 4/2010, A. Zaporozhetz 10
 Measuring Risk: ERR Variance: A measure of the dispersion of a set of data points around their mean value. Variance measures the variability (volatility) from an average. Volatility is a measure of risk, so this statistic can help determine the risk an investor might take on when purchasing a specific security. The variance of an asset’s expected return is the expected value of the squared deviations from the expected returns. WIUU BF 1, v. 4/2010, A. Zaporozhetz 11
Measuring Risk: ERR Variance: A measure of the dispersion of a set of data points around their mean value. Variance measures the variability (volatility) from an average. Volatility is a measure of risk, so this statistic can help determine the risk an investor might take on when purchasing a specific security. The variance of an asset’s expected return is the expected value of the squared deviations from the expected returns. WIUU BF 1, v. 4/2010, A. Zaporozhetz 11
 Measuring Risk: ERR Standard deviation: Square root of Variance. A measure of the dispersion of a set of data from its mean. The more spread apart the data, the higher the deviation. In finance, it is a measure of total risk of a financial asset. WIUU BF 1, v. 4/2010, A. Zaporozhetz 12
Measuring Risk: ERR Standard deviation: Square root of Variance. A measure of the dispersion of a set of data from its mean. The more spread apart the data, the higher the deviation. In finance, it is a measure of total risk of a financial asset. WIUU BF 1, v. 4/2010, A. Zaporozhetz 12
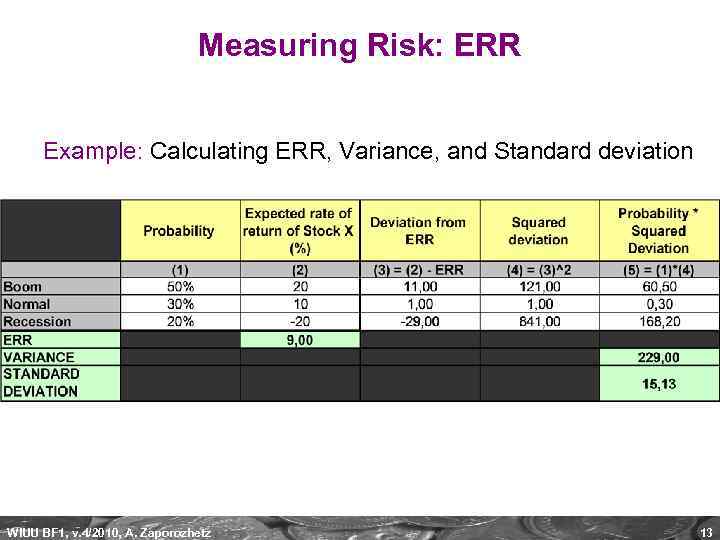 Measuring Risk: ERR Example: Calculating ERR, Variance, and Standard deviation WIUU BF 1, v. 4/2010, A. Zaporozhetz 13
Measuring Risk: ERR Example: Calculating ERR, Variance, and Standard deviation WIUU BF 1, v. 4/2010, A. Zaporozhetz 13
 Measuring Risk: Historical RR Variance: The variance of an asset’s historical returns is the sum of the squared deviations divided by (n-1). Standard deviation: Square root of variance. WIUU BF 1, v. 4/2010, A. Zaporozhetz 14
Measuring Risk: Historical RR Variance: The variance of an asset’s historical returns is the sum of the squared deviations divided by (n-1). Standard deviation: Square root of variance. WIUU BF 1, v. 4/2010, A. Zaporozhetz 14
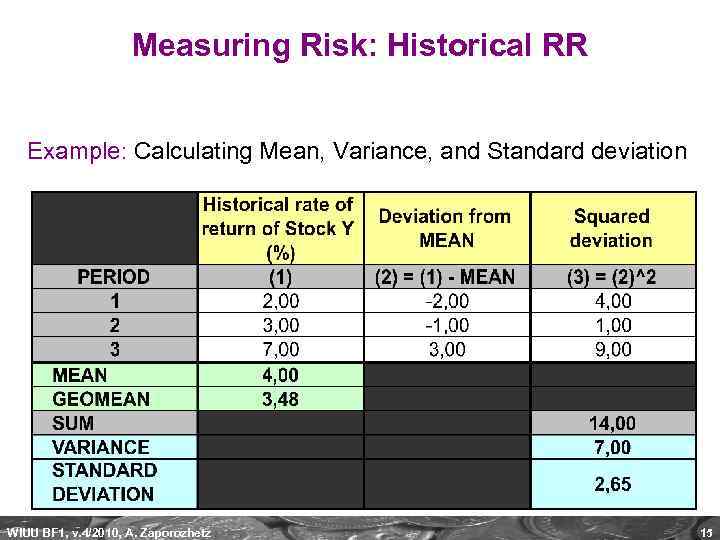 Measuring Risk: Historical RR Example: Calculating Mean, Variance, and Standard deviation WIUU BF 1, v. 4/2010, A. Zaporozhetz 15
Measuring Risk: Historical RR Example: Calculating Mean, Variance, and Standard deviation WIUU BF 1, v. 4/2010, A. Zaporozhetz 15
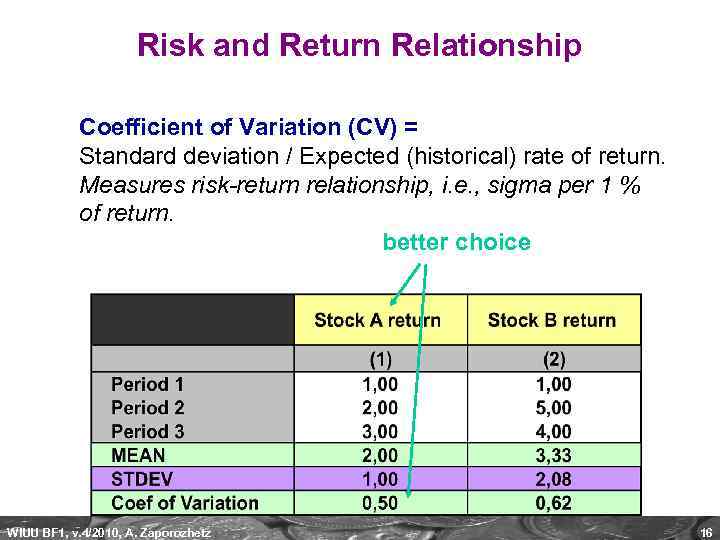 Risk and Return Relationship Coefficient of Variation (CV) = Standard deviation / Expected (historical) rate of return. Measures risk-return relationship, i. e. , sigma per 1 % of return. better choice WIUU BF 1, v. 4/2010, A. Zaporozhetz 16
Risk and Return Relationship Coefficient of Variation (CV) = Standard deviation / Expected (historical) rate of return. Measures risk-return relationship, i. e. , sigma per 1 % of return. better choice WIUU BF 1, v. 4/2010, A. Zaporozhetz 16
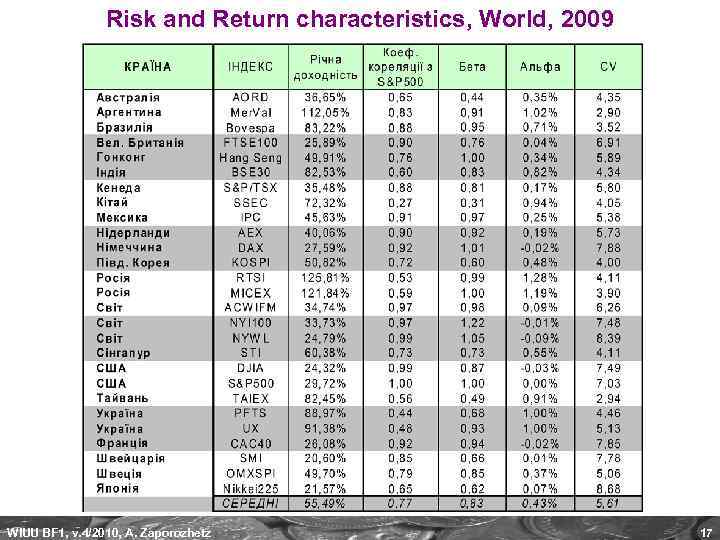 Risk and Return characteristics, World, 2009 WIUU BF 1, v. 4/2010, A. Zaporozhetz 17
Risk and Return characteristics, World, 2009 WIUU BF 1, v. 4/2010, A. Zaporozhetz 17
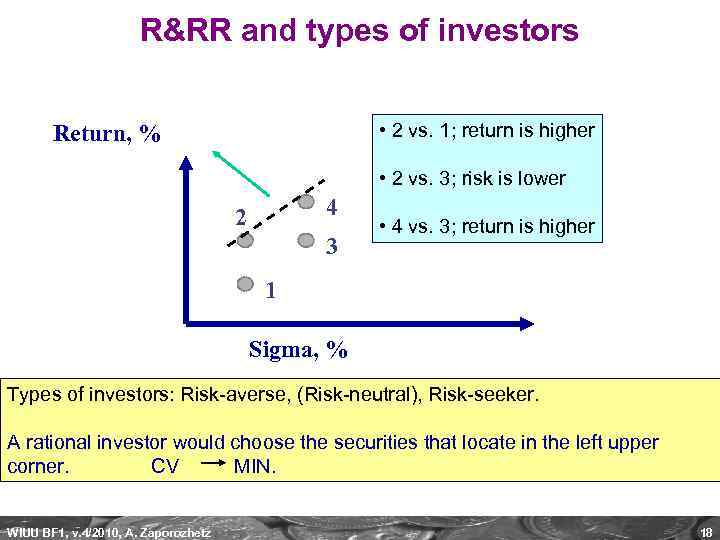 R&RR and types of investors • 2 vs. 1; return is higher Return, % • 2 vs. 3; risk is lower 4 2 3 • 4 vs. 3; return is higher 1 Sigma, % Types of investors: Risk-averse, (Risk-neutral), Risk-seeker. A rational investor would choose the securities that locate in the left upper corner. CV MIN. WIUU BF 1, v. 4/2010, A. Zaporozhetz 18
R&RR and types of investors • 2 vs. 1; return is higher Return, % • 2 vs. 3; risk is lower 4 2 3 • 4 vs. 3; return is higher 1 Sigma, % Types of investors: Risk-averse, (Risk-neutral), Risk-seeker. A rational investor would choose the securities that locate in the left upper corner. CV MIN. WIUU BF 1, v. 4/2010, A. Zaporozhetz 18
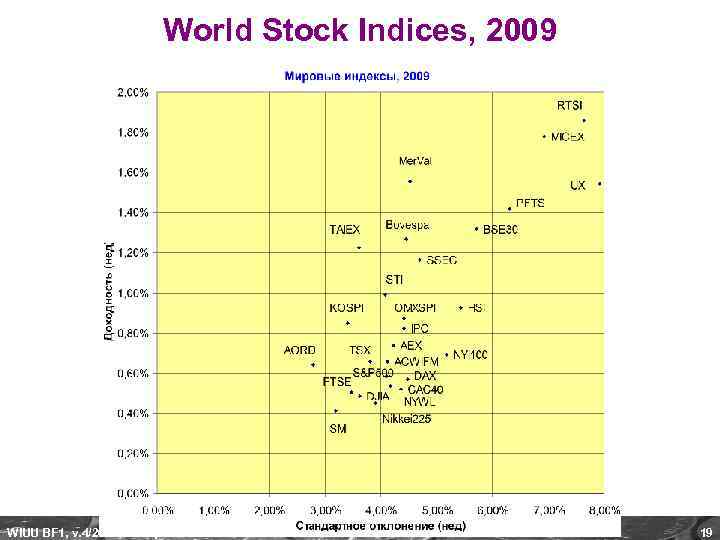 World Stock Indices, 2009 WIUU BF 1, v. 4/2010, A. Zaporozhetz 19
World Stock Indices, 2009 WIUU BF 1, v. 4/2010, A. Zaporozhetz 19
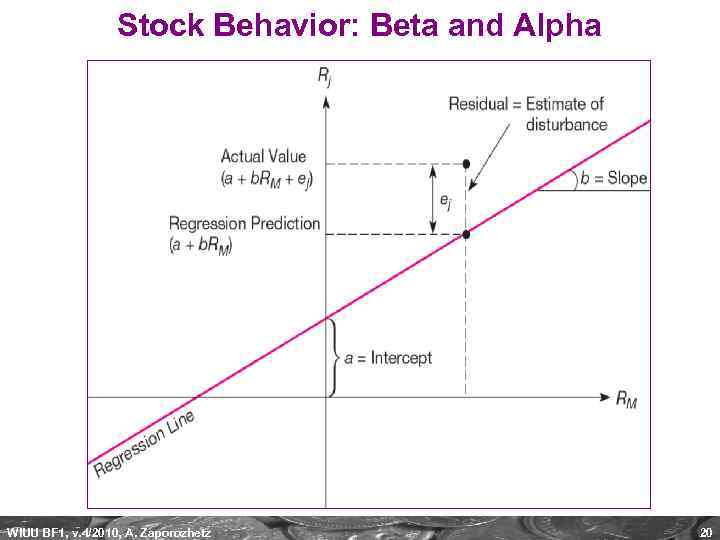 Stock Behavior: Beta and Alpha WIUU BF 1, v. 4/2010, A. Zaporozhetz 20
Stock Behavior: Beta and Alpha WIUU BF 1, v. 4/2010, A. Zaporozhetz 20
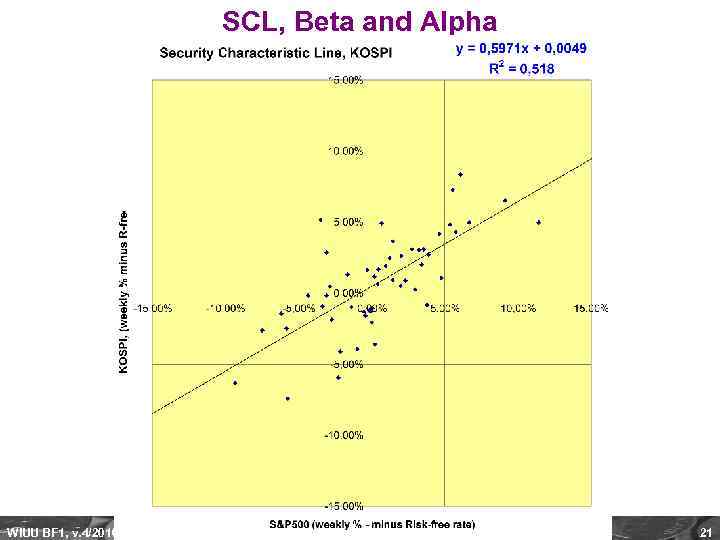 SCL, Beta and Alpha WIUU BF 1, v. 4/2010, A. Zaporozhetz 21
SCL, Beta and Alpha WIUU BF 1, v. 4/2010, A. Zaporozhetz 21
 Beta: A measure of systematic risk, of a security (or a portfolio) in comparison to the market (market index, proxy). Measure of elasticity. Equals the variable coefficient “b” in the linear regression equation: Y = a + b*X + ε Graphically, Beta = Y / X A beta of greater than 1 indicates that the security's price is more volatile than the market, more risky. “Aggressive” security. The Security characteristic line is more steep. A beta of less than 1 indicates that the security's price is less volatile than the market, less risky. “Defensive” security. WIUU BF 1, v. 4/2010, A. Zaporozhetz 22
Beta: A measure of systematic risk, of a security (or a portfolio) in comparison to the market (market index, proxy). Measure of elasticity. Equals the variable coefficient “b” in the linear regression equation: Y = a + b*X + ε Graphically, Beta = Y / X A beta of greater than 1 indicates that the security's price is more volatile than the market, more risky. “Aggressive” security. The Security characteristic line is more steep. A beta of less than 1 indicates that the security's price is less volatile than the market, less risky. “Defensive” security. WIUU BF 1, v. 4/2010, A. Zaporozhetz 22
 Total Risk: Components Systematic Risk - The risk inherent to the entire market, or market segment. Also known as “non-diversifiable risk" or "market risk. " E. g. , interest rates, recession and wars represent sources of systematic risk because they affect the entire market and cannot be avoided through diversification. Affects a broad range of securities. Even a portfolio of well-diversified assets cannot escape all risk. Measured with BETA. Unsystematic Risk – Company-specific risk that is inherent in each investment. Can be reduced through appropriate diversification (=strategy designed to reduce risk by spreading the portfolio across many investments. Also known as "specific risk", "diversifiable risk“, or "residual risk". E. g. , a sudden strike by the employees of a company is considered to be unsystematic risk. WIUU BF 1, v. 4/2010, A. Zaporozhetz 23
Total Risk: Components Systematic Risk - The risk inherent to the entire market, or market segment. Also known as “non-diversifiable risk" or "market risk. " E. g. , interest rates, recession and wars represent sources of systematic risk because they affect the entire market and cannot be avoided through diversification. Affects a broad range of securities. Even a portfolio of well-diversified assets cannot escape all risk. Measured with BETA. Unsystematic Risk – Company-specific risk that is inherent in each investment. Can be reduced through appropriate diversification (=strategy designed to reduce risk by spreading the portfolio across many investments. Also known as "specific risk", "diversifiable risk“, or "residual risk". E. g. , a sudden strike by the employees of a company is considered to be unsystematic risk. WIUU BF 1, v. 4/2010, A. Zaporozhetz 23
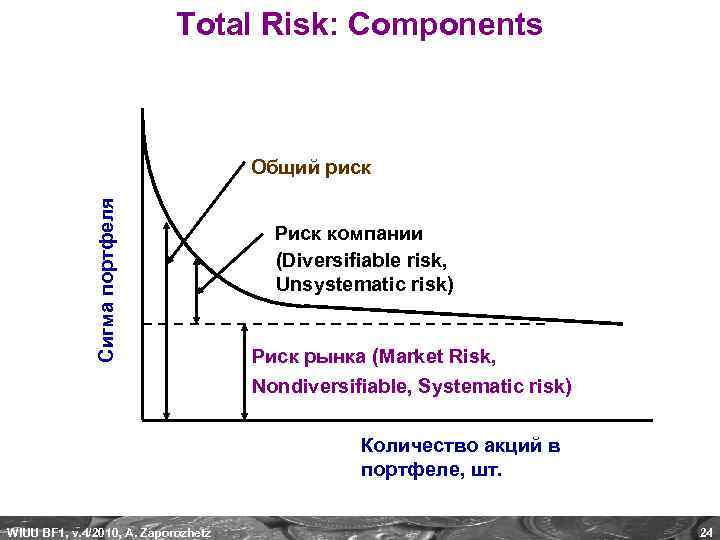 Total Risk: Components Сигма портфеля Общий риск Риск компании (Diversifiable risk, Unsystematic risk) Риск рынка (Market Risk, Nondiversifiable, Systematic risk) Количество акций в портфеле, шт. WIUU BF 1, v. 4/2010, A. Zaporozhetz 24
Total Risk: Components Сигма портфеля Общий риск Риск компании (Diversifiable risk, Unsystematic risk) Риск рынка (Market Risk, Nondiversifiable, Systematic risk) Количество акций в портфеле, шт. WIUU BF 1, v. 4/2010, A. Zaporozhetz 24
 Безрисковая доходность WIUU BF 1, v. 4/2010, A. Zaporozhetz 25
Безрисковая доходность WIUU BF 1, v. 4/2010, A. Zaporozhetz 25
 Безрисковая доходность WIUU BF 1, v. 4/2010, A. Zaporozhetz 26
Безрисковая доходность WIUU BF 1, v. 4/2010, A. Zaporozhetz 26
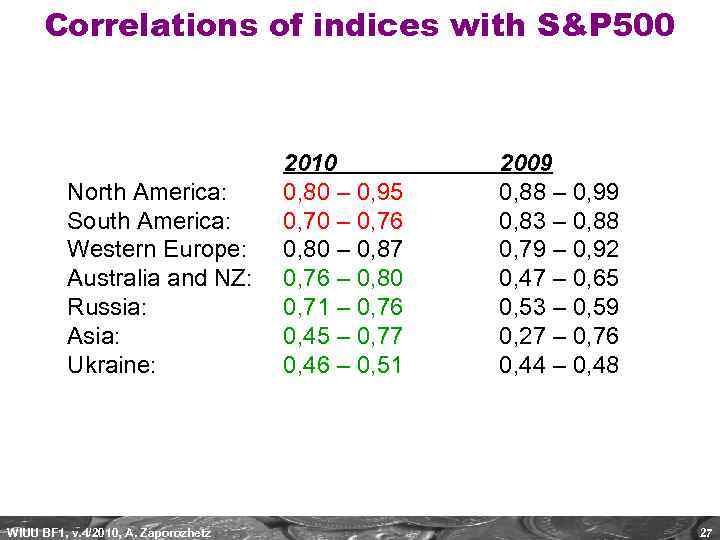 Correlations of indices with S&P 500 2010 North America: 0, 80 – 0, 95 South America: 0, 70 – 0, 76 Western Europe: 0, 80 – 0, 87 Australia and NZ: 0, 76 – 0, 80 Russia: 0, 71 – 0, 76 Asia: 0, 45 – 0, 77 Ukraine: 0, 46 – 0, 51 WIUU BF 1, v. 4/2010, A. Zaporozhetz 2009 0, 88 – 0, 99 0, 83 – 0, 88 0, 79 – 0, 92 0, 47 – 0, 65 0, 53 – 0, 59 0, 27 – 0, 76 0, 44 – 0, 48 27
Correlations of indices with S&P 500 2010 North America: 0, 80 – 0, 95 South America: 0, 70 – 0, 76 Western Europe: 0, 80 – 0, 87 Australia and NZ: 0, 76 – 0, 80 Russia: 0, 71 – 0, 76 Asia: 0, 45 – 0, 77 Ukraine: 0, 46 – 0, 51 WIUU BF 1, v. 4/2010, A. Zaporozhetz 2009 0, 88 – 0, 99 0, 83 – 0, 88 0, 79 – 0, 92 0, 47 – 0, 65 0, 53 – 0, 59 0, 27 – 0, 76 0, 44 – 0, 48 27
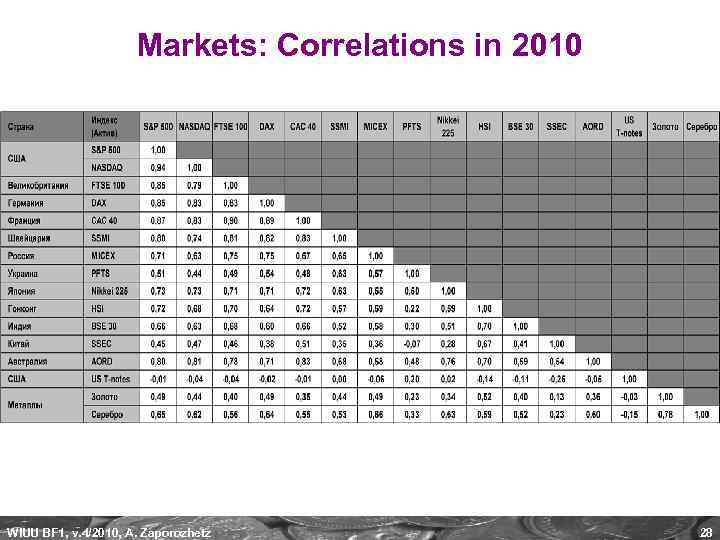 Markets: Correlations in 2010 WIUU BF 1, v. 4/2010, A. Zaporozhetz 28
Markets: Correlations in 2010 WIUU BF 1, v. 4/2010, A. Zaporozhetz 28
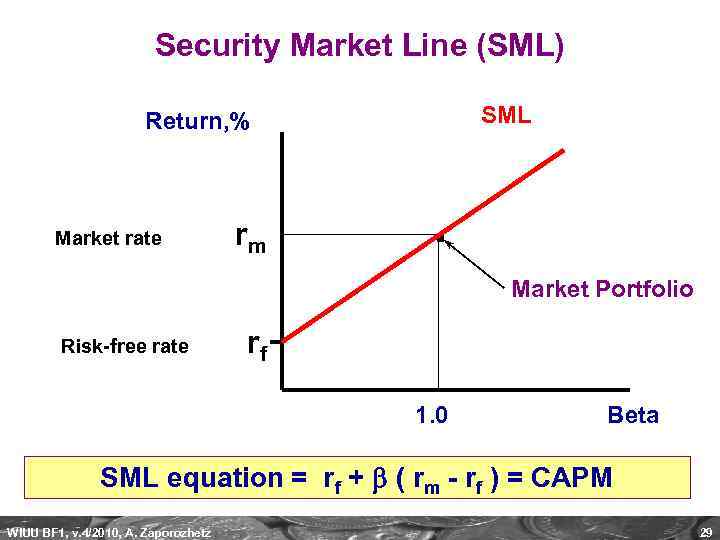 Security Market Line (SML) SML Return, % Market rate rm . Market Portfolio Risk-free rate rf 1. 0 Beta SML equation = rf + ( rm - rf ) = CAPM WIUU BF 1, v. 4/2010, A. Zaporozhetz 29
Security Market Line (SML) SML Return, % Market rate rm . Market Portfolio Risk-free rate rf 1. 0 Beta SML equation = rf + ( rm - rf ) = CAPM WIUU BF 1, v. 4/2010, A. Zaporozhetz 29
 Sample Calculations for SML rm = 13%, rf = 3% x = 1. 20, then: E(rx) = 3% + 1. 2*(13%-3%) = 15% y = 0. 80, then: E(ry) = 3% + 0. 8*(13%-3%) = 11% WIUU BF 1, v. 4/2010, A. Zaporozhetz 30
Sample Calculations for SML rm = 13%, rf = 3% x = 1. 20, then: E(rx) = 3% + 1. 2*(13%-3%) = 15% y = 0. 80, then: E(ry) = 3% + 0. 8*(13%-3%) = 11% WIUU BF 1, v. 4/2010, A. Zaporozhetz 30
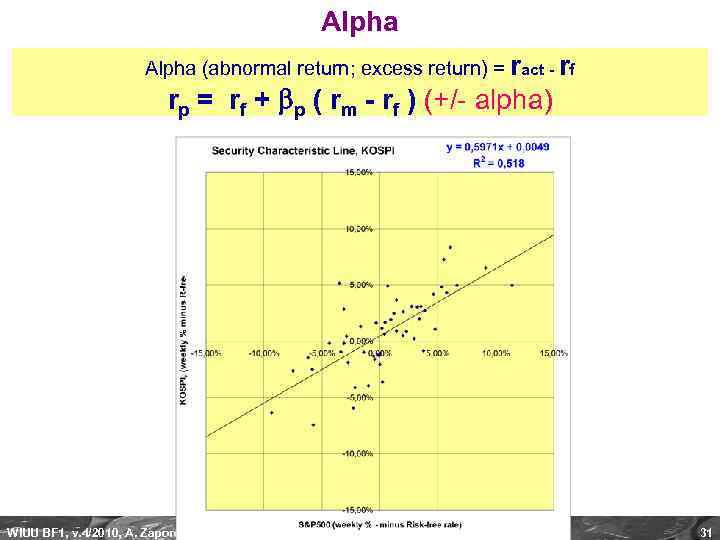 Alpha (abnormal return; excess return) = ract - rf rp = rf + p ( rm - rf ) (+/- alpha) WIUU BF 1, v. 4/2010, A. Zaporozhetz 31
Alpha (abnormal return; excess return) = ract - rf rp = rf + p ( rm - rf ) (+/- alpha) WIUU BF 1, v. 4/2010, A. Zaporozhetz 31
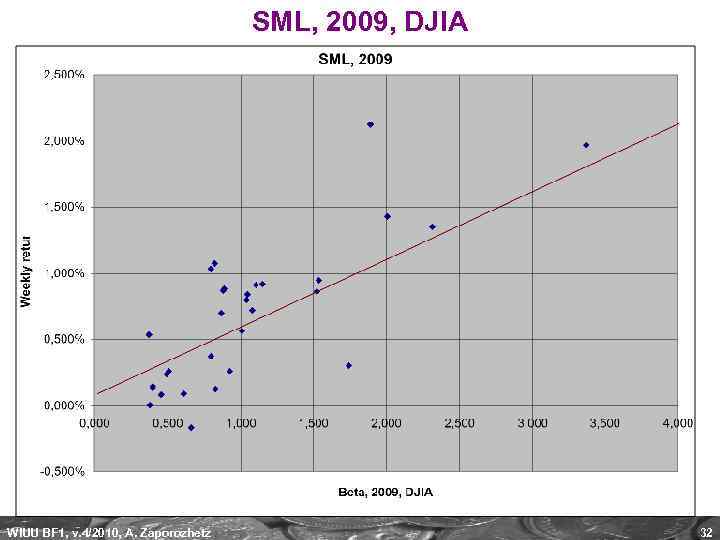 SML, 2009, DJIA WIUU BF 1, v. 4/2010, A. Zaporozhetz 32
SML, 2009, DJIA WIUU BF 1, v. 4/2010, A. Zaporozhetz 32
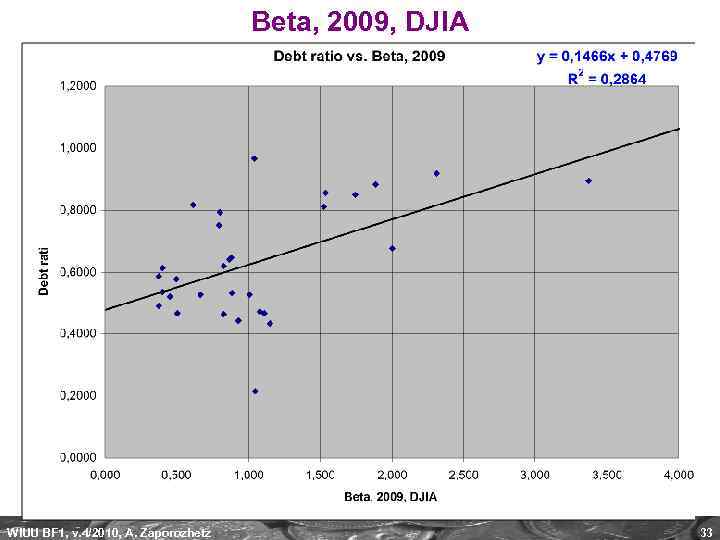 Beta, 2009, DJIA WIUU BF 1, v. 4/2010, A. Zaporozhetz 33
Beta, 2009, DJIA WIUU BF 1, v. 4/2010, A. Zaporozhetz 33
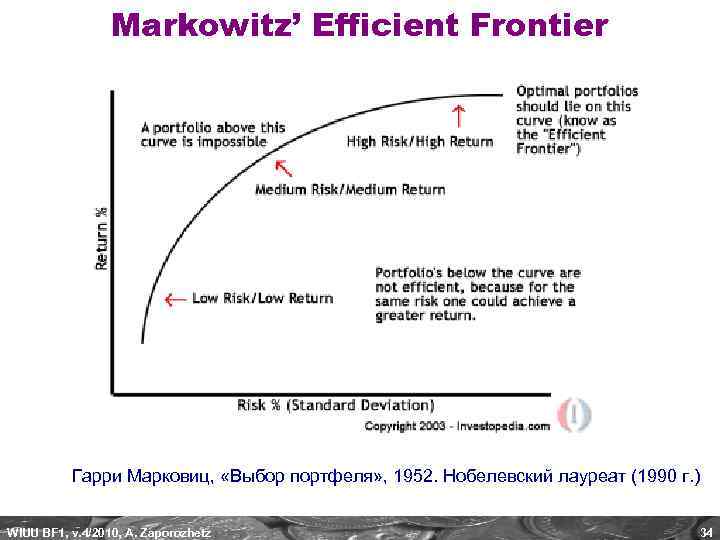 Markowitz’ Efficient Frontier Гарри Марковиц, «Выбор портфеля» , 1952. Нобелевский лауреат (1990 г. ) WIUU BF 1, v. 4/2010, A. Zaporozhetz 34
Markowitz’ Efficient Frontier Гарри Марковиц, «Выбор портфеля» , 1952. Нобелевский лауреат (1990 г. ) WIUU BF 1, v. 4/2010, A. Zaporozhetz 34
 Coefficient of Determination WIUU BF 1, v. 4/2010, A. Zaporozhetz 35
Coefficient of Determination WIUU BF 1, v. 4/2010, A. Zaporozhetz 35
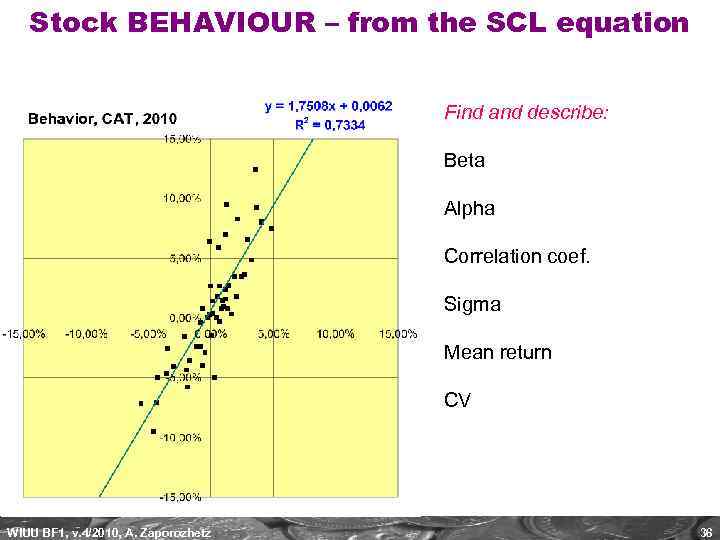 Stock BEHAVIOUR – from the SCL equation Find and describe: Beta Alpha Correlation coef. Sigma Mean return CV WIUU BF 1, v. 4/2010, A. Zaporozhetz 36
Stock BEHAVIOUR – from the SCL equation Find and describe: Beta Alpha Correlation coef. Sigma Mean return CV WIUU BF 1, v. 4/2010, A. Zaporozhetz 36
 Class Risk and Return Additional materials (Advanced level) WIUU BF 1, v. 4/2010, A. Zaporozhetz 37
Class Risk and Return Additional materials (Advanced level) WIUU BF 1, v. 4/2010, A. Zaporozhetz 37
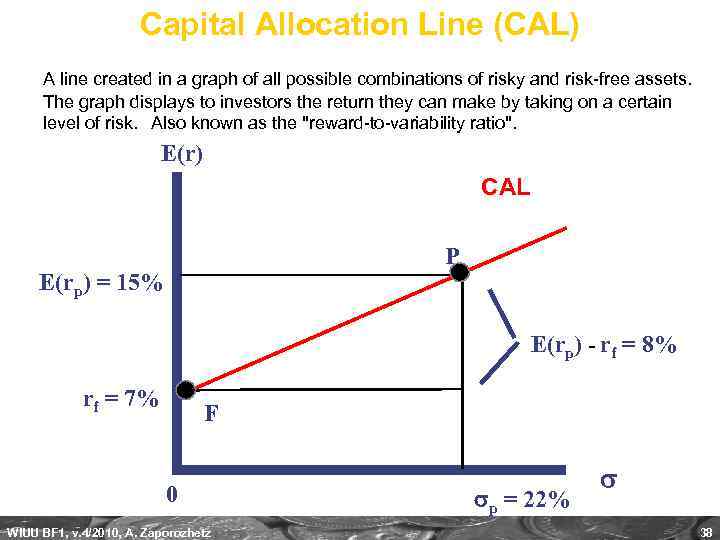 Capital Allocation Line (CAL) A line created in a graph of all possible combinations of risky and risk-free assets. The graph displays to investors the return they can make by taking on a certain level of risk. Also known as the "reward-to-variability ratio". E(r) CAL P E(rp) = 15% E(rp) - rf = 8% rf = 7% F 0 WIUU BF 1, v. 4/2010, A. Zaporozhetz p = 22% 38
Capital Allocation Line (CAL) A line created in a graph of all possible combinations of risky and risk-free assets. The graph displays to investors the return they can make by taking on a certain level of risk. Also known as the "reward-to-variability ratio". E(r) CAL P E(rp) = 15% E(rp) - rf = 8% rf = 7% F 0 WIUU BF 1, v. 4/2010, A. Zaporozhetz p = 22% 38
 Portfolio risk and return: Return The rate of return on a portfolio is a weighted average of the rates of return of each asset comprising the portfolio, with the portfolio proportions ($) as weights. rp = w 1 r 1 + w 2 r 2 w 1 = Proportion of funds in Security 1, % w 2 = Proportion of funds in Security 2, % r 1 = Expected return on Security 1, % r 2 = Expected return on Security 2, % WIUU BF 1, v. 4/2010, A. Zaporozhetz 39
Portfolio risk and return: Return The rate of return on a portfolio is a weighted average of the rates of return of each asset comprising the portfolio, with the portfolio proportions ($) as weights. rp = w 1 r 1 + w 2 r 2 w 1 = Proportion of funds in Security 1, % w 2 = Proportion of funds in Security 2, % r 1 = Expected return on Security 1, % r 2 = Expected return on Security 2, % WIUU BF 1, v. 4/2010, A. Zaporozhetz 39
 Portfolio risk and return: Covariance is a measure of the linear association between the 2 variables. A measure of the degree to which returns on two risky assets move in tandem. A positive covariance means that asset returns move together. A negative covariance means that returns move inversely. Covariance between Stock 1 and Stock 2 = OR: WIUU BF 1, v. 4/2010, A. Zaporozhetz 40
Portfolio risk and return: Covariance is a measure of the linear association between the 2 variables. A measure of the degree to which returns on two risky assets move in tandem. A positive covariance means that asset returns move together. A negative covariance means that returns move inversely. Covariance between Stock 1 and Stock 2 = OR: WIUU BF 1, v. 4/2010, A. Zaporozhetz 40
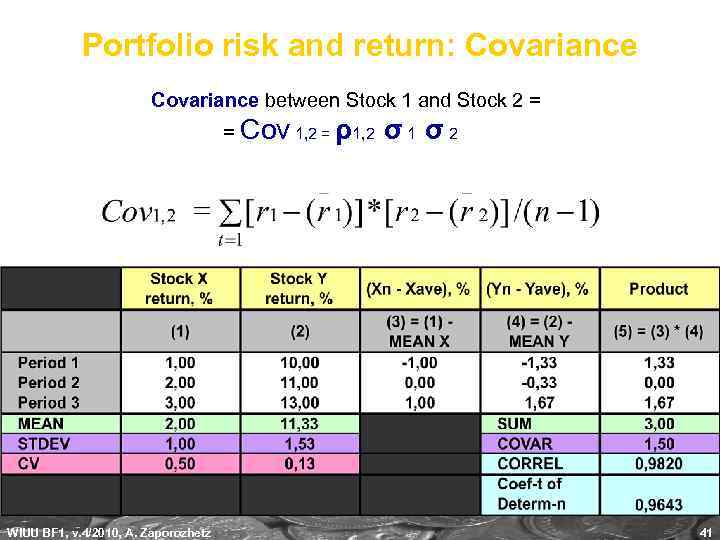 Portfolio risk and return: Covariance between Stock 1 and Stock 2 = = Cov 1, 2 = ρ1, 2 σ 1 σ 2 WIUU BF 1, v. 4/2010, A. Zaporozhetz 41
Portfolio risk and return: Covariance between Stock 1 and Stock 2 = = Cov 1, 2 = ρ1, 2 σ 1 σ 2 WIUU BF 1, v. 4/2010, A. Zaporozhetz 41
 Portfolio risk and return: Correlation is a measure of the linear association between the 2 variables. In the world of finance, a statistical measure of how two securities move in relation to each other. ρ 1, 2 = Cov 1, 2 / σ 1 σ 2 Correlation coefficient is ALWAYS [-1; 1]. Perfect positive correlation (a correlation coefficient of +1) implies that as one security moves, either up or down, the other security will move in lockstep, in the same direction. Alternatively, perfect negative correlation means that if one security moves in either direction the security that is perfectly negatively correlated will move by an equal amount in the opposite direction. If the correlation is 0, the movements of the securities are said to have no correlation; they are completely random. WIUU BF 1, v. 4/2010, A. Zaporozhetz 42
Portfolio risk and return: Correlation is a measure of the linear association between the 2 variables. In the world of finance, a statistical measure of how two securities move in relation to each other. ρ 1, 2 = Cov 1, 2 / σ 1 σ 2 Correlation coefficient is ALWAYS [-1; 1]. Perfect positive correlation (a correlation coefficient of +1) implies that as one security moves, either up or down, the other security will move in lockstep, in the same direction. Alternatively, perfect negative correlation means that if one security moves in either direction the security that is perfectly negatively correlated will move by an equal amount in the opposite direction. If the correlation is 0, the movements of the securities are said to have no correlation; they are completely random. WIUU BF 1, v. 4/2010, A. Zaporozhetz 42
 Portfolio risk and return: Sigma When two risky assets with variances 12 and 22, respectively, are combined into a portfolio with portfolio weights w 1 and w 2, respectively, the portfolio variance is given by: p 2 = w 12 12 + w 22 22 + 2 w 1 w 2 Cov(r 1 r 2) = = w 12 12 + w 22 22 + 2 w 1 w 2 ρ 1 2 Hence, the portfolio’s standard deviation - p - is the square root of the above formula. WIUU BF 1, v. 4/2010, A. Zaporozhetz 43
Portfolio risk and return: Sigma When two risky assets with variances 12 and 22, respectively, are combined into a portfolio with portfolio weights w 1 and w 2, respectively, the portfolio variance is given by: p 2 = w 12 12 + w 22 22 + 2 w 1 w 2 Cov(r 1 r 2) = = w 12 12 + w 22 22 + 2 w 1 w 2 ρ 1 2 Hence, the portfolio’s standard deviation - p - is the square root of the above formula. WIUU BF 1, v. 4/2010, A. Zaporozhetz 43
 Portfolio risk and return: Sigma Rule: When a risky asset is combined with a risk-free asset, the portfolio standard deviation equals the risky asset’s standard deviation multiplied by the portfolio proportion invested in the risky asset. WIUU BF 1, v. 4/2010, A. Zaporozhetz 44
Portfolio risk and return: Sigma Rule: When a risky asset is combined with a risk-free asset, the portfolio standard deviation equals the risky asset’s standard deviation multiplied by the portfolio proportion invested in the risky asset. WIUU BF 1, v. 4/2010, A. Zaporozhetz 44
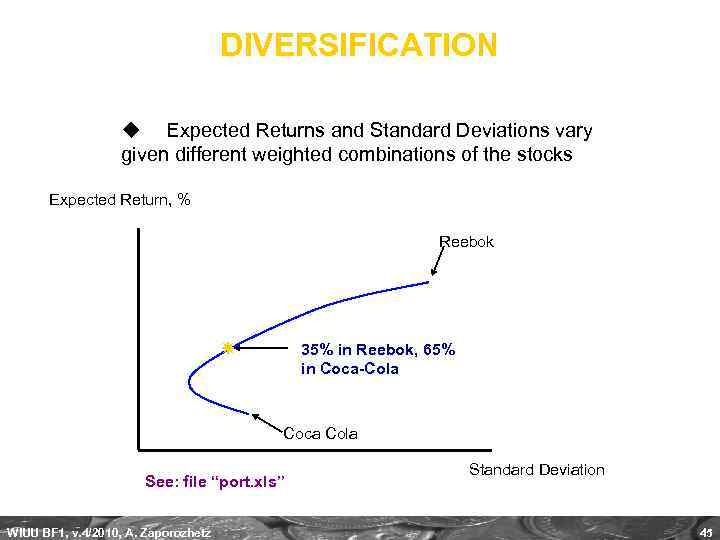 DIVERSIFICATION u Expected Returns and Standard Deviations vary given different weighted combinations of the stocks Expected Return, % Reebok 35% in Reebok, 65% in Coca-Cola Coca Cola See: file “port. xls” WIUU BF 1, v. 4/2010, A. Zaporozhetz Standard Deviation 45
DIVERSIFICATION u Expected Returns and Standard Deviations vary given different weighted combinations of the stocks Expected Return, % Reebok 35% in Reebok, 65% in Coca-Cola Coca Cola See: file “port. xls” WIUU BF 1, v. 4/2010, A. Zaporozhetz Standard Deviation 45
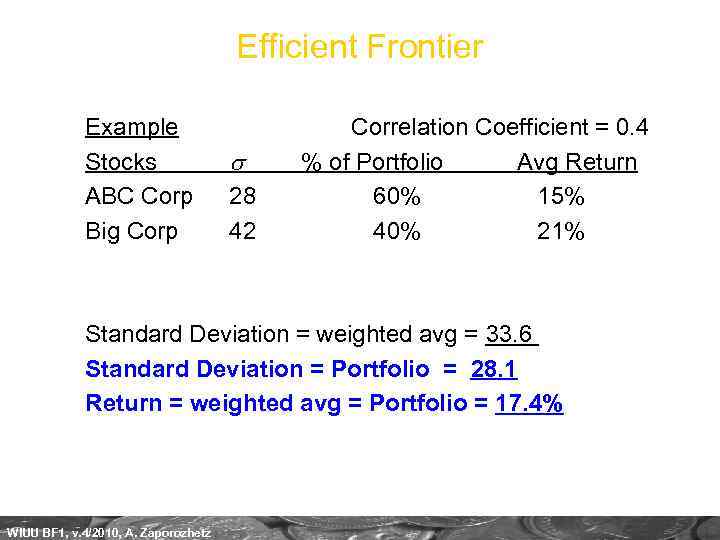 Efficient Frontier Example Correlation Coefficient = 0. 4 Stocks s % of Portfolio Avg Return ABC Corp 28 60% 15% Big Corp 42 40% 21% Standard Deviation = weighted avg = 33. 6 Standard Deviation = Portfolio = 28. 1 Return = weighted avg = Portfolio = 17. 4% WIUU BF 1, v. 4/2010, A. Zaporozhetz
Efficient Frontier Example Correlation Coefficient = 0. 4 Stocks s % of Portfolio Avg Return ABC Corp 28 60% 15% Big Corp 42 40% 21% Standard Deviation = weighted avg = 33. 6 Standard Deviation = Portfolio = 28. 1 Return = weighted avg = Portfolio = 17. 4% WIUU BF 1, v. 4/2010, A. Zaporozhetz
 Efficient Frontier Example Correlation Coefficient = 0. 4 Stocks s % of Portfolio Avg Return ABC Corp 28 60% 15% Big Corp 42 40% 21% Standard Deviation = weighted avg = 33. 6 Standard Deviation = Portfolio = 28. 1 Return = weighted avg = Portfolio = 17. 4% Let’s Add stock New Corp to the portfolio WIUU BF 1, v. 4/2010, A. Zaporozhetz
Efficient Frontier Example Correlation Coefficient = 0. 4 Stocks s % of Portfolio Avg Return ABC Corp 28 60% 15% Big Corp 42 40% 21% Standard Deviation = weighted avg = 33. 6 Standard Deviation = Portfolio = 28. 1 Return = weighted avg = Portfolio = 17. 4% Let’s Add stock New Corp to the portfolio WIUU BF 1, v. 4/2010, A. Zaporozhetz
 Efficient Frontier Example Correlation Coefficient = 0. 3 Stocks s % of Portfolio Avg Return Portfolio 28. 1 50% 17. 4% New Corp 30 50% 19% NEW Standard Deviation = weighted avg = 31. 80 NEW Standard Deviation = Portfolio = 23. 43 NEW Return = weighted avg = Portfolio = 18. 20% WIUU BF 1, v. 4/2010, A. Zaporozhetz
Efficient Frontier Example Correlation Coefficient = 0. 3 Stocks s % of Portfolio Avg Return Portfolio 28. 1 50% 17. 4% New Corp 30 50% 19% NEW Standard Deviation = weighted avg = 31. 80 NEW Standard Deviation = Portfolio = 23. 43 NEW Return = weighted avg = Portfolio = 18. 20% WIUU BF 1, v. 4/2010, A. Zaporozhetz
 Efficient Frontier Example Correlation Coefficient = 0. 3 Stocks s % of Portfolio Avg Return Portfolio 28. 1 50% 17. 4% New Corp 30 50% 19% NEW Standard Deviation = weighted avg = 31. 80 NEW Standard Deviation = Portfolio = 23. 43 NEW Return = weighted avg = Portfolio = 18. 20% NOTE: Higher return & Lower risk How did we do that? DIVERSIFICATION WIUU BF 1, v. 4/2010, A. Zaporozhetz
Efficient Frontier Example Correlation Coefficient = 0. 3 Stocks s % of Portfolio Avg Return Portfolio 28. 1 50% 17. 4% New Corp 30 50% 19% NEW Standard Deviation = weighted avg = 31. 80 NEW Standard Deviation = Portfolio = 23. 43 NEW Return = weighted avg = Portfolio = 18. 20% NOTE: Higher return & Lower risk How did we do that? DIVERSIFICATION WIUU BF 1, v. 4/2010, A. Zaporozhetz
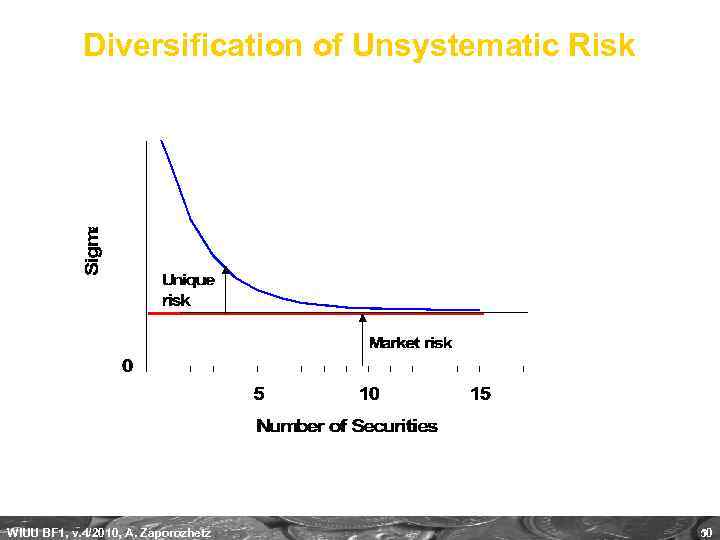 Diversification of Unsystematic Risk WIUU BF 1, v. 4/2010, A. Zaporozhetz 50
Diversification of Unsystematic Risk WIUU BF 1, v. 4/2010, A. Zaporozhetz 50
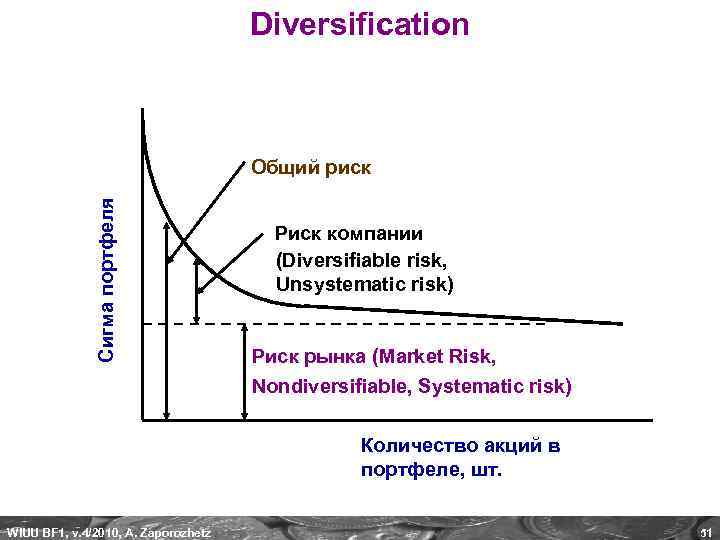 Diversification Сигма портфеля Общий риск Риск компании (Diversifiable risk, Unsystematic risk) Риск рынка (Market Risk, Nondiversifiable, Systematic risk) Количество акций в портфеле, шт. WIUU BF 1, v. 4/2010, A. Zaporozhetz 51
Diversification Сигма портфеля Общий риск Риск компании (Diversifiable risk, Unsystematic risk) Риск рынка (Market Risk, Nondiversifiable, Systematic risk) Количество акций в портфеле, шт. WIUU BF 1, v. 4/2010, A. Zaporozhetz 51
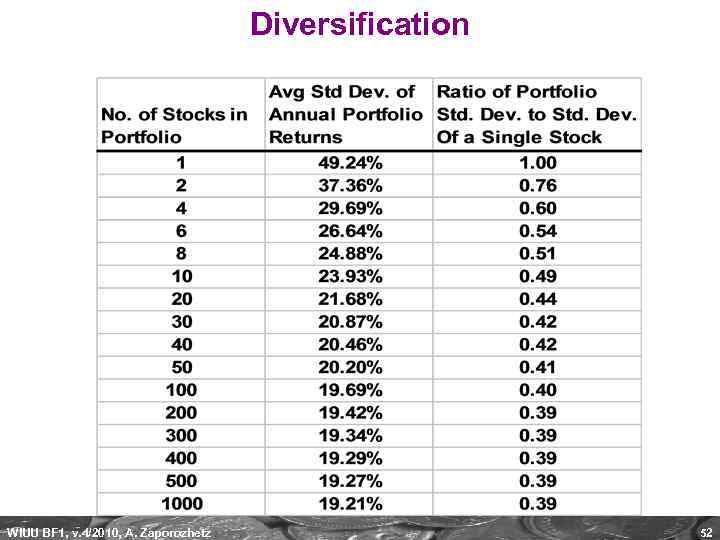 Diversification WIUU BF 1, v. 4/2010, A. Zaporozhetz 52
Diversification WIUU BF 1, v. 4/2010, A. Zaporozhetz 52
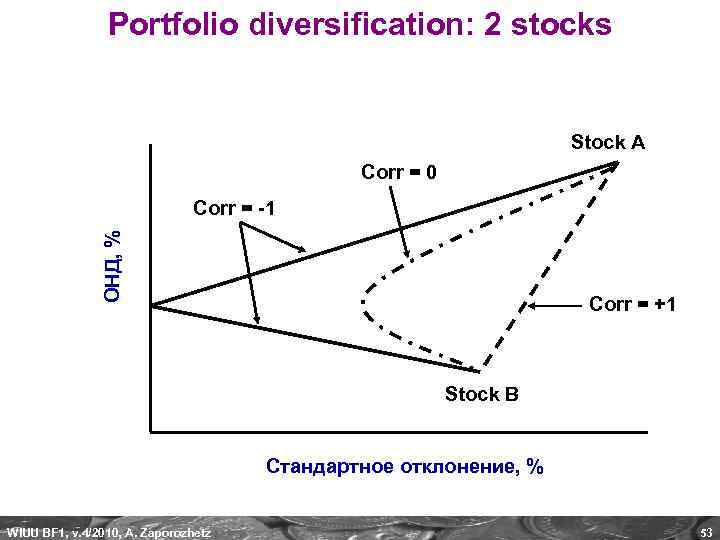 Portfolio diversification: 2 stocks Stock A Corr = 0 ОНД, % Corr = -1 Corr = +1 Stock B Стандартное отклонение, % WIUU BF 1, v. 4/2010, A. Zaporozhetz 53
Portfolio diversification: 2 stocks Stock A Corr = 0 ОНД, % Corr = -1 Corr = +1 Stock B Стандартное отклонение, % WIUU BF 1, v. 4/2010, A. Zaporozhetz 53
 Efficient Frontier • Each half egg shell represents the possible weighted combinations for two stocks. • The composite of all stock sets constitutes the efficient frontier Expected Return, % Standard Deviation WIUU BF 1, v. 4/2010, A. Zaporozhetz 54
Efficient Frontier • Each half egg shell represents the possible weighted combinations for two stocks. • The composite of all stock sets constitutes the efficient frontier Expected Return, % Standard Deviation WIUU BF 1, v. 4/2010, A. Zaporozhetz 54
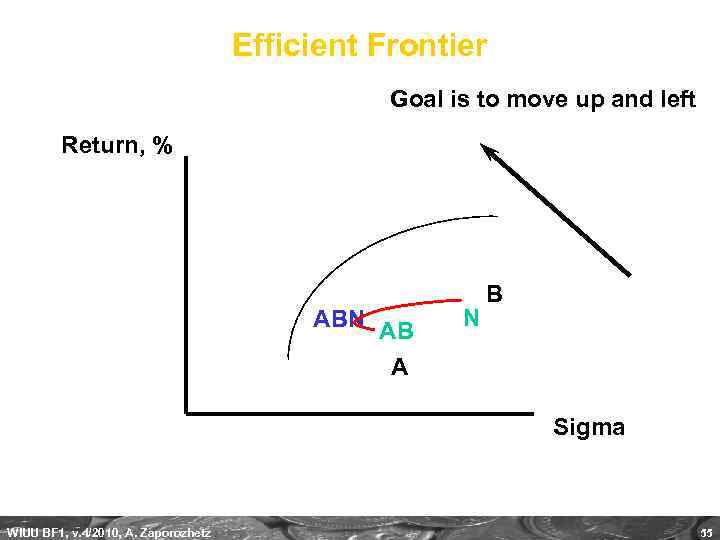 Efficient Frontier Goal is to move up and left Return, % ABN AB A N B Sigma WIUU BF 1, v. 4/2010, A. Zaporozhetz 55
Efficient Frontier Goal is to move up and left Return, % ABN AB A N B Sigma WIUU BF 1, v. 4/2010, A. Zaporozhetz 55
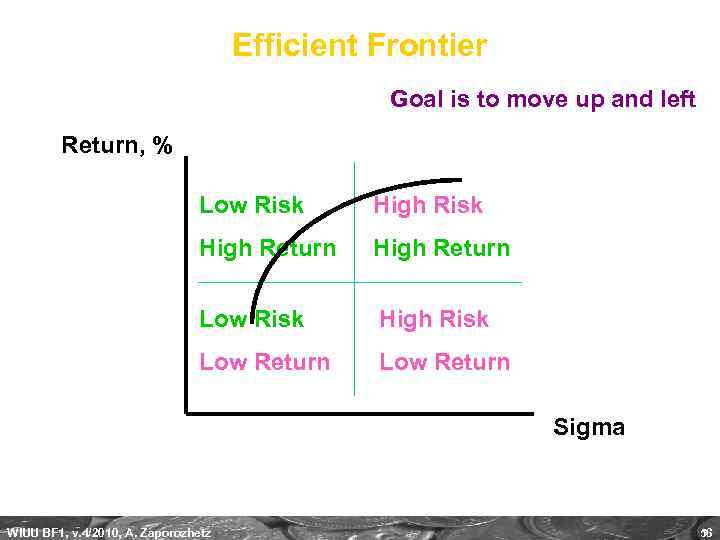 Efficient Frontier Goal is to move up and left Return, % Low Risk High Return Low Risk High Risk Low Return Sigma WIUU BF 1, v. 4/2010, A. Zaporozhetz 56
Efficient Frontier Goal is to move up and left Return, % Low Risk High Return Low Risk High Risk Low Return Sigma WIUU BF 1, v. 4/2010, A. Zaporozhetz 56
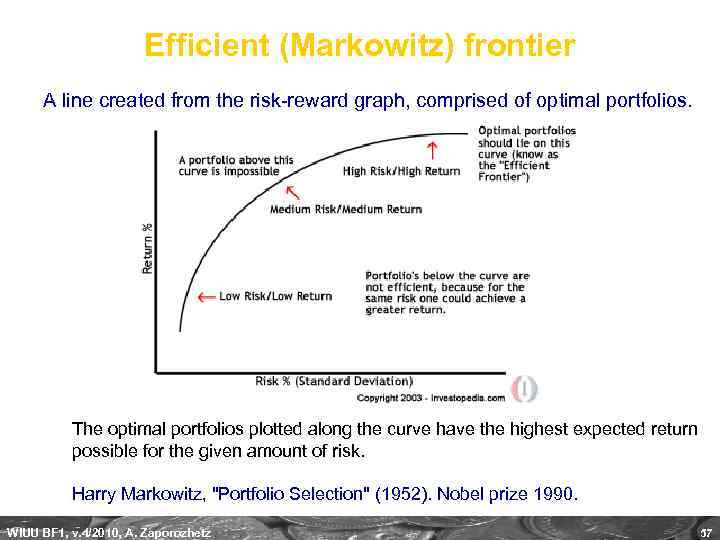 Efficient (Markowitz) frontier A line created from the risk-reward graph, comprised of optimal portfolios. The optimal portfolios plotted along the curve have the highest expected return possible for the given amount of risk. Harry Markowitz, "Portfolio Selection" (1952). Nobel prize 1990. WIUU BF 1, v. 4/2010, A. Zaporozhetz 57
Efficient (Markowitz) frontier A line created from the risk-reward graph, comprised of optimal portfolios. The optimal portfolios plotted along the curve have the highest expected return possible for the given amount of risk. Harry Markowitz, "Portfolio Selection" (1952). Nobel prize 1990. WIUU BF 1, v. 4/2010, A. Zaporozhetz 57
 Political Risks: Mechel Story “В четверг (25 июля) премьер-министр Владимир Путин встретился в Нижнем Новгороде с представителями крупнейших российских металлургических и угольных компаний и высказался о ситуации на российском рынке стали. Премьер-министр неожиданно сделал ряд жестких заявлений в отношении Мечела (ОАО «ЧМЗ» ). По сути, он обвинил компанию в нерыночном поведении и предположил, что прокуратуре следуетобратить внимание на торговую деятельность компании. Этих заявлений оказалось достаточно, чтобы обрушить котировки Мечела – с четверга они упали на 37, 6%, заставив инвесторов гадать о будущем компании – ведущего производителя коксующегося угля в России. ” «Тройка-Диалог» , 25 июля 2008 г. (www. troika. ru) WIUU BF 1, v. 4/2010, A. Zaporozhetz 58
Political Risks: Mechel Story “В четверг (25 июля) премьер-министр Владимир Путин встретился в Нижнем Новгороде с представителями крупнейших российских металлургических и угольных компаний и высказался о ситуации на российском рынке стали. Премьер-министр неожиданно сделал ряд жестких заявлений в отношении Мечела (ОАО «ЧМЗ» ). По сути, он обвинил компанию в нерыночном поведении и предположил, что прокуратуре следуетобратить внимание на торговую деятельность компании. Этих заявлений оказалось достаточно, чтобы обрушить котировки Мечела – с четверга они упали на 37, 6%, заставив инвесторов гадать о будущем компании – ведущего производителя коксующегося угля в России. ” «Тройка-Диалог» , 25 июля 2008 г. (www. troika. ru) WIUU BF 1, v. 4/2010, A. Zaporozhetz 58
 Political Risks WIUU BF 1, v. 4/2010, A. Zaporozhetz 59
Political Risks WIUU BF 1, v. 4/2010, A. Zaporozhetz 59
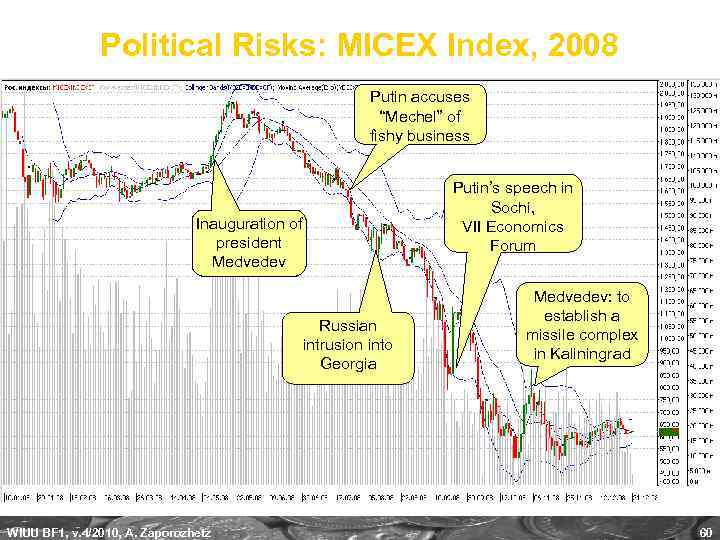 Political Risks: MICEX Index, 2008 Putin accuses “Mechel” of fishy business Inauguration of president Medvedev Russian intrusion into Georgia WIUU BF 1, v. 4/2010, A. Zaporozhetz Putin’s speech in Sochi, VII Economics Forum Medvedev: to establish a missile complex in Kaliningrad 60
Political Risks: MICEX Index, 2008 Putin accuses “Mechel” of fishy business Inauguration of president Medvedev Russian intrusion into Georgia WIUU BF 1, v. 4/2010, A. Zaporozhetz Putin’s speech in Sochi, VII Economics Forum Medvedev: to establish a missile complex in Kaliningrad 60
 Portfolio risk and return: Beta Systematic Risk - The risk inherent to the entire market, or market segment. Also known as "un-diversifiable risk" or "market risk. " E. g. , interest rates, recession and wars represent sources of systematic risk because they affect the entire market and cannot be avoided through diversification. Affects a broad range of securities. Even a portfolio of welldiversified assets cannot escape all risk. Measured with BETA. Still, one can diversify the systematic risk – in the sense that one can choose securities with different betas (defensive vs. aggressive stocks) and combine them. WIUU BF 1, v. 4/2010, A. Zaporozhetz 61
Portfolio risk and return: Beta Systematic Risk - The risk inherent to the entire market, or market segment. Also known as "un-diversifiable risk" or "market risk. " E. g. , interest rates, recession and wars represent sources of systematic risk because they affect the entire market and cannot be avoided through diversification. Affects a broad range of securities. Even a portfolio of welldiversified assets cannot escape all risk. Measured with BETA. Still, one can diversify the systematic risk – in the sense that one can choose securities with different betas (defensive vs. aggressive stocks) and combine them. WIUU BF 1, v. 4/2010, A. Zaporozhetz 61
 Portfolio risk and return: Beta The Beta of a portfolio is the weighted average of the rates of return of each asset comprising the portfolio, with the portfolio proportions ($) as weights. bp = w 1 b 1 + w 2 b 2 w 1 = Proportion of funds in Security 1, % w 2 = Proportion of funds in Security 2, % b 1 = Beta of Security 1 b 2 = Beta of Security 2 WIUU BF 1, v. 4/2010, A. Zaporozhetz 62
Portfolio risk and return: Beta The Beta of a portfolio is the weighted average of the rates of return of each asset comprising the portfolio, with the portfolio proportions ($) as weights. bp = w 1 b 1 + w 2 b 2 w 1 = Proportion of funds in Security 1, % w 2 = Proportion of funds in Security 2, % b 1 = Beta of Security 1 b 2 = Beta of Security 2 WIUU BF 1, v. 4/2010, A. Zaporozhetz 62
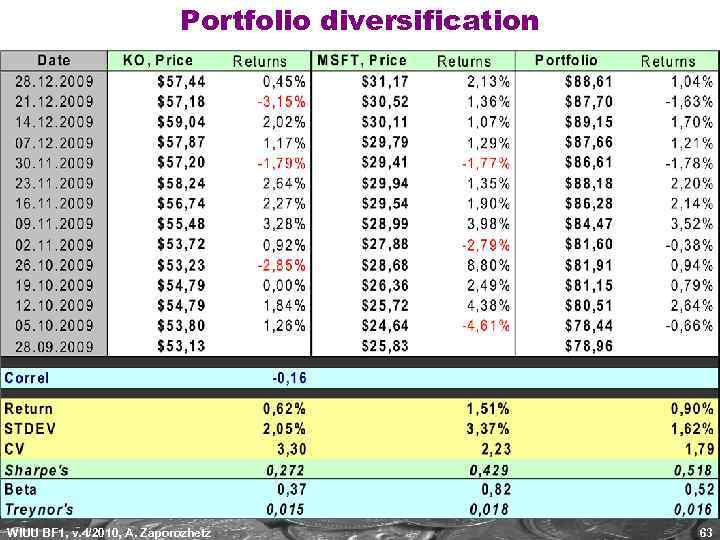 Portfolio diversification WIUU BF 1, v. 4/2010, A. Zaporozhetz 63
Portfolio diversification WIUU BF 1, v. 4/2010, A. Zaporozhetz 63


