Class 1 -2 R R CAPM Portfolio MGT Diversification

Class 1 -2 R&R. CAPM. Portfolio MGT Diversification. 2 -asset portfolio. Sharpe’s and Treynor’s measures. Portfolio MGT strategies and techniques. Study materials: RWJ: Ch. 9, 10 WIUU BF-2, Fall 2013, A. Zaporozhetz 1

CORE CONCEPTS Return, % = P 1 / P 0 - 1 P 1 – P 0 (+ ∑ Dividends) HPR, % = P 0 CV = sigma / mean return WIUU BF-2, Fall 2013, A. Zaporozhetz 2

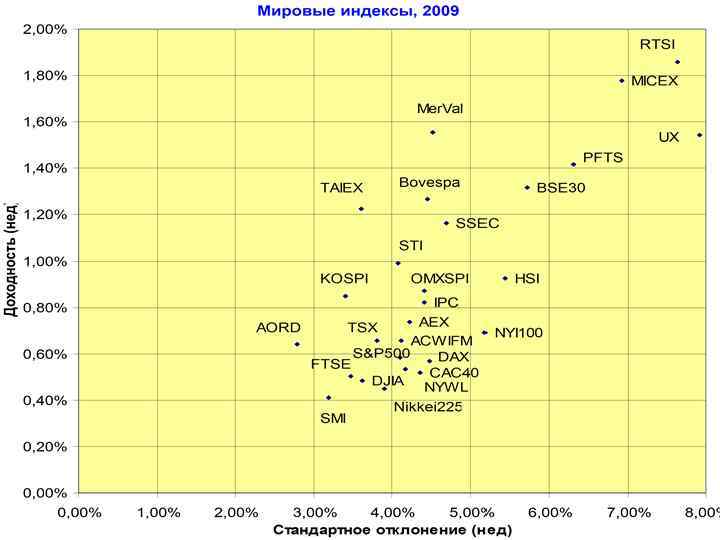Risk and return relationship, 2009 WIUU BF-2, Fall 2013, A. Zaporozhetz 3

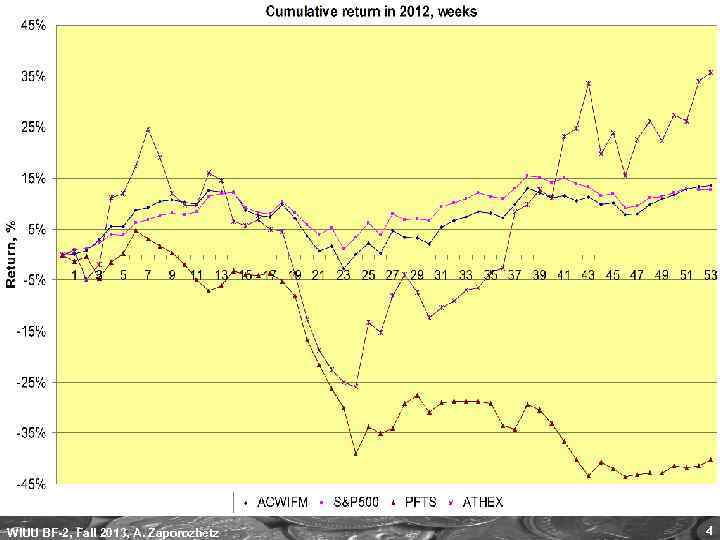WIUU BF-2, Fall 2013, A. Zaporozhetz 4

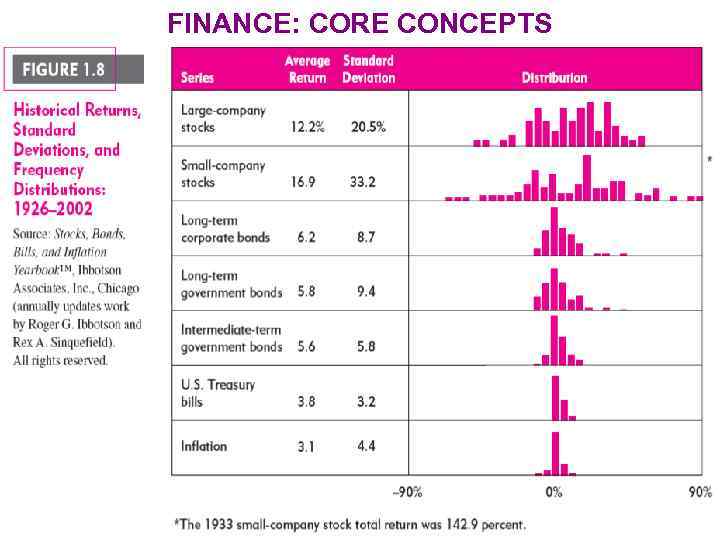FINANCE: CORE CONCEPTS 2. Risk and return relationship WIUU BF-2, Fall 2013, A. Zaporozhetz 5

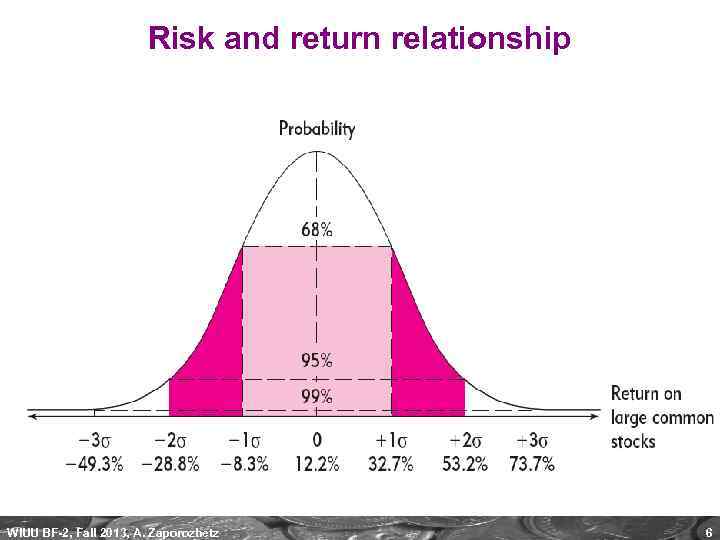Risk and return relationship WIUU BF-2, Fall 2013, A. Zaporozhetz 6

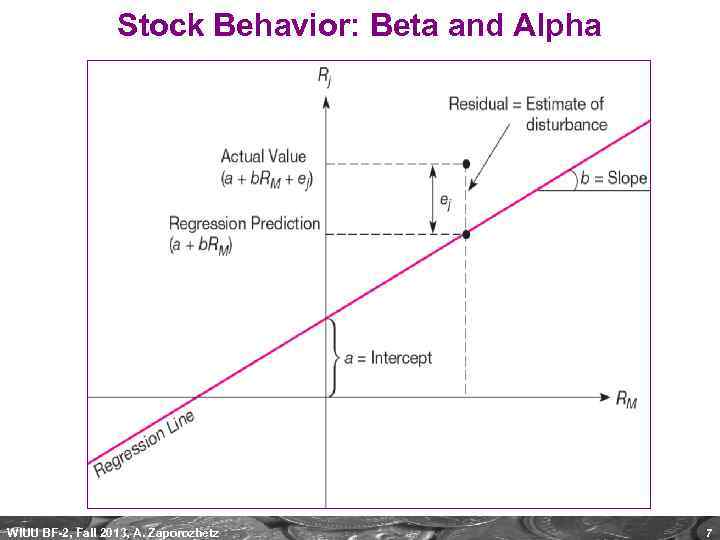Stock Behavior: Beta and Alpha WIUU BF-2, Fall 2013, A. Zaporozhetz 7

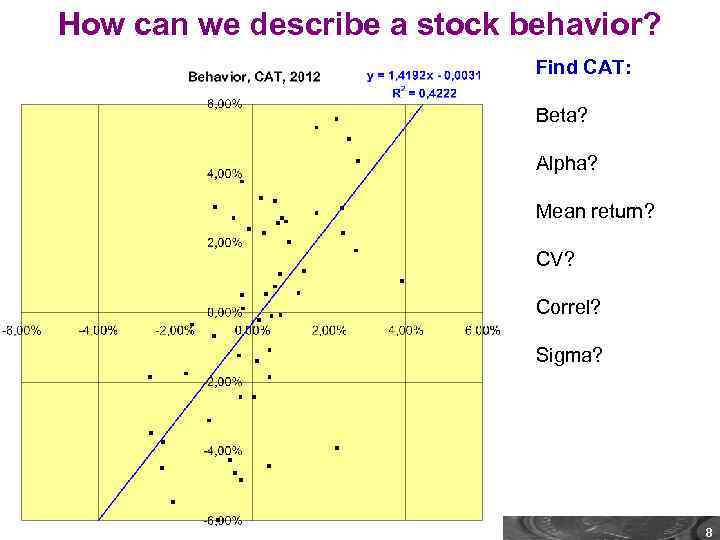How can we describe a stock behavior? Find CAT: Beta? Alpha? Mean return? CV? Correl? Sigma? WIUU BF-2, Fall 2013, A. Zaporozhetz 8

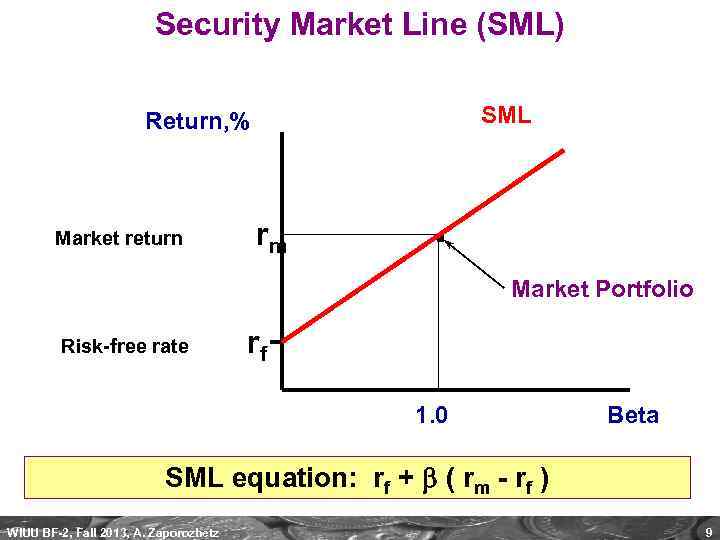Security Market Line (SML) SML Return, % Market return rm . Market Portfolio Risk-free rate rf 1. 0 Beta SML equation: rf + ( rm - rf ) WIUU BF-2, Fall 2013, A. Zaporozhetz 9

Portfolio is a combination of financial assets (stocks, bonds, etc). In theory of investments, we study a 2 -asset portfolio behavior. If you invested $50, 000 this way: $20, 000 into CAT stocks and $30, 000 into WMT stocks, then your portfolio in fully-invested (no spare cash), with their components’ weights of 40% and 60% respectively. All stock indices could be considered as fully-invested portfolios. WIUU BF-2, Fall 2013, A. Zaporozhetz 10

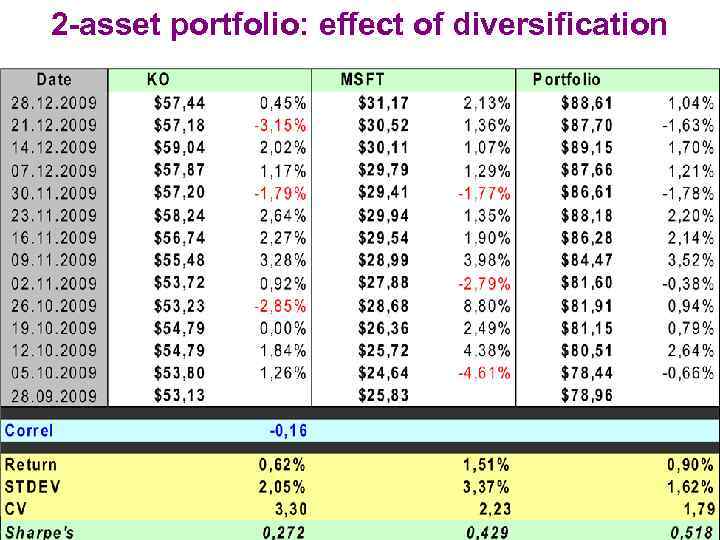2 -asset portfolio: effect of diversification WIUU BF-2, Fall 2013, A. Zaporozhetz 11

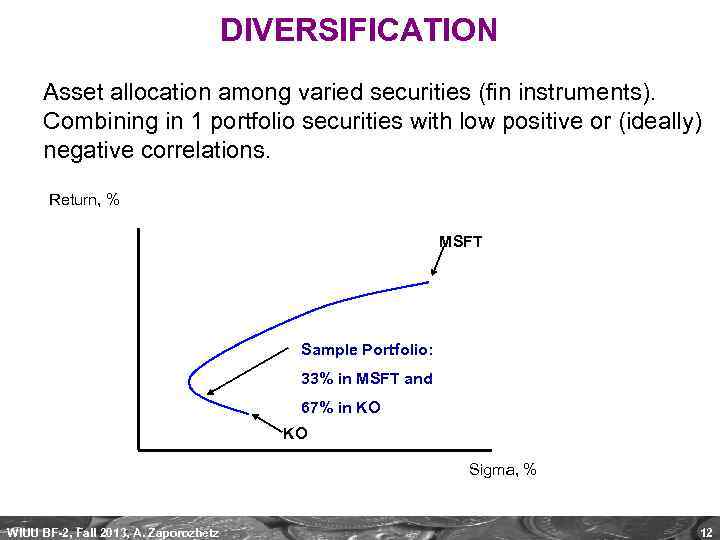DIVERSIFICATION Asset allocation among varied securities (fin instruments). Combining in 1 portfolio securities with low positive or (ideally) negative correlations. Return, % MSFT Sample Portfolio: 33% in MSFT and 67% in KO KO Sigma, % WIUU BF-2, Fall 2013, A. Zaporozhetz 12

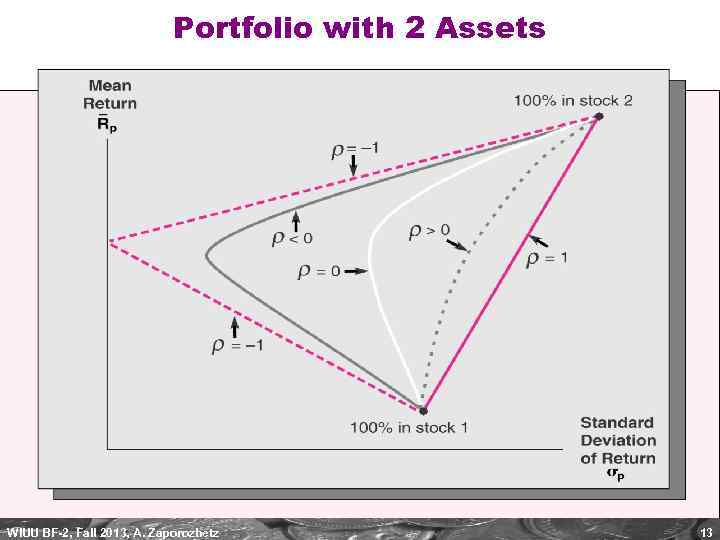Portfolio with 2 Assets WIUU BF-2, Fall 2013, A. Zaporozhetz 13

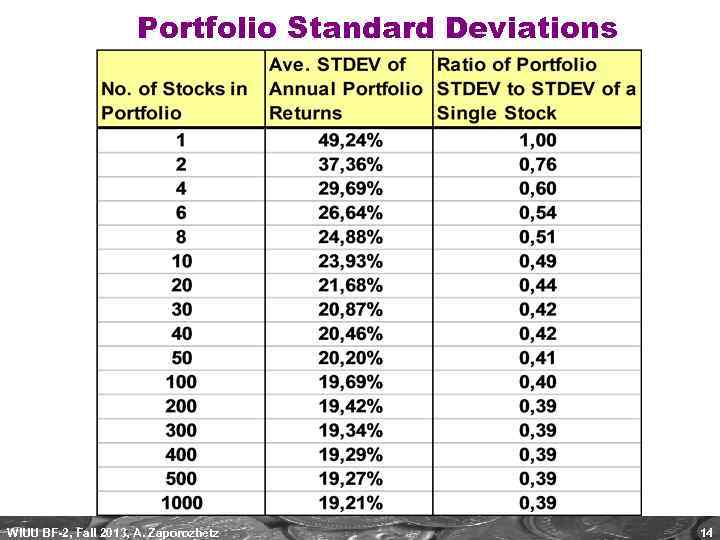Portfolio Standard Deviations WIUU BF-2, Fall 2013, A. Zaporozhetz 14

Portfolio Risk: STDEV Components of total risk Total risk Unsystematic risk (Diversifiable risk, Company-specific risk) Systematic Risk (Non-diversifiable, Market risk) Number of Stocks in Portfolio WIUU BF-2, Fall 2013, A. Zaporozhetz 15

Unsystematic risk Несистематический риск (диверсифицируемый риск, собственный риск; non-systematic risk, diversifiable risk, company-specific risk, unique risk, σe). Часть общего риска финансового актива. Связан с внутренними факторами как эмитента, так и поведения участников рынка (продавцов и покупателей). Его значение будет различаться в зависимости от того, против какого рынка (индекса) мы измеряем систематический риск инструмента. Этот риск устраняется частично или полностью при помощи диверсификации активов в инвестиционном портфеле. WIUU BF-2, Fall 2013, A. Zaporozhetz 16

Portfolio MGT Definition Actual return, CAPM-return Sigma CV Portfolio characteristic line (PCL) Beta Alpha Portfolio MGT measures (ratios): Sharpe’s Treynor’s Unsystematic risk (diversifiable risk) WIUU BF-2, Fall 2013, A. Zaporozhetz 17

Portfolio: return The rate of return on a portfolio is a weighted average of the rates of return of each asset comprising the portfolio, with the portfolio proportions ($) as weights. rp = w 1 r 1 + w 2 r 2 w 1 = Proportion of funds in Security 1, % w 2 = Proportion of funds in Security 2, % r 1 = Expected return on Security 1, % r 2 = Expected return on Security 2, % WIUU BF-2, Fall 2013, A. Zaporozhetz 18

Portfolio: Total risk (sigma) When two risky assets with variances 12 and 22, respectively, are combined into a portfolio with portfolio weights w 1 and w 2, respectively, the portfolio variance is given by: p 2 = w 12 12 + w 22 22 + 2 w 1 w 2 Cov(r 1 r 2) = = w 12 12 + w 22 22 + 2 w 1 w 2 ρ 1 2 Hence, the portfolio’s standard deviation is the square root of the above. WIUU BF-2, Fall 2013, A. Zaporozhetz 19

Portfolio: Sigma Rule: Sigma of a 2 -stock portfolio is the weighted average of the 2 sigmas, ONLY when those 2 stocks are perfectly positively correlated. Rule: When a risky asset is combined with a risk-free asset, the portfolio standard deviation equals the risky asset’s standard deviation multiplied by the portfolio proportion invested in the risky asset. WIUU BF-2, Fall 2013, A. Zaporozhetz 20

Portfolio systematic risk: Beta The Beta of a portfolio is the weighted average of the rates of return of each asset comprising the portfolio, with the portfolio proportions ($) as weights. ßp = w 1 ß 1 + w 2 ß 2 w 1 = Proportion of funds in Security 1, % w 2 = Proportion of funds in Security 2, % ß 1 = Beta of Security 1 ß 2 = Beta of Security 2 WIUU BF-2, Fall 2013, A. Zaporozhetz 21

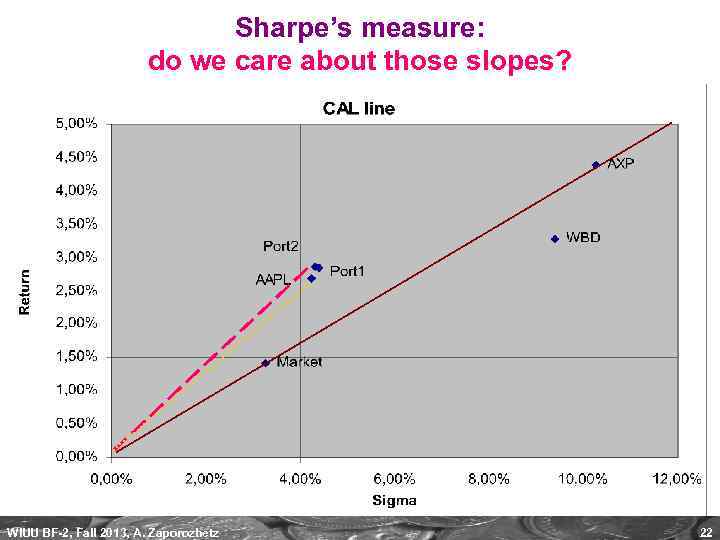Sharpe’s measure: do we care about those slopes? WIUU BF-2, Fall 2013, A. Zaporozhetz 22

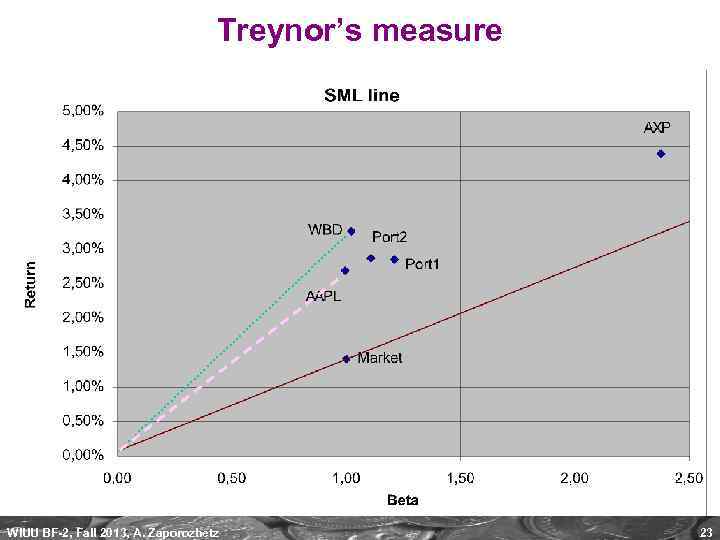Treynor’s measure WIUU BF-2, Fall 2013, A. Zaporozhetz 23

Minimum Variance & Sigma Portfolio For a two-stock portfolio, the minimum sigma portfolio, weight on Asset AXP is: Example: Correl = 0. 57, r(AXP) = 0. 20% and = 4. 71% r(INTC) = 0. 10% and = 3. 11% Therefore, for minimum variance invest in 9% of AXP and 91% of INTC. WIUU BF-2, Fall 2013, A. Zaporozhetz 24

Portfolio MGT: Techniques 1. Reduce your portfolio’s sigma though diversification. 2. Choose stocks with positive alphas. BUT mind the effect of 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. momentum. When the market is growing, choose aggressive stocks. “Buy&hold” vs. Active trading. Costs vs. benefits? Technical analysis vs. Fundamental analysis Long positions vs. Short positions If volatility / uncertainty / ambiguity is going higher, stay in your money. Monitor your portfolio performance regularly. Combine various measurements (ratios) to get a fuller picture. Past is a good indicator of the Future? NOT always. “Re-shake” your portfolio if needs be. Watch your profits/losses. Watch your cash flows. WIUU BF-2, Fall 2013, A. Zaporozhetz 25

World Indices WIUU BF-2, Fall 2013, A. Zaporozhetz 26

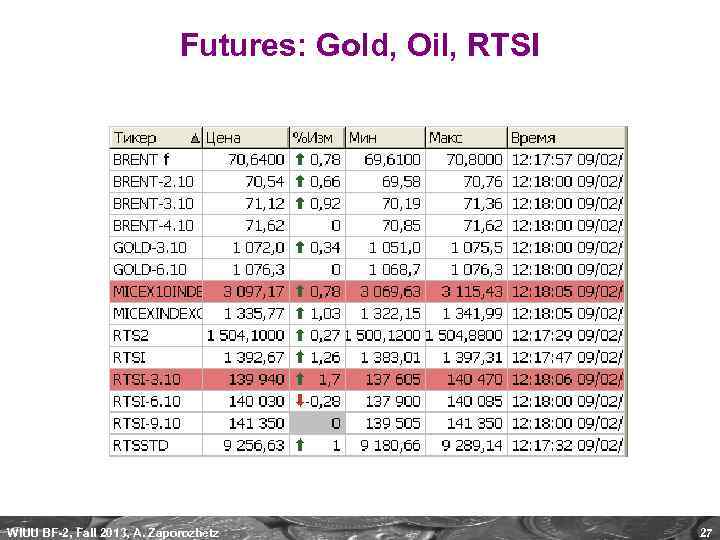Futures: Gold, Oil, RTSI WIUU BF-2, Fall 2013, A. Zaporozhetz 27

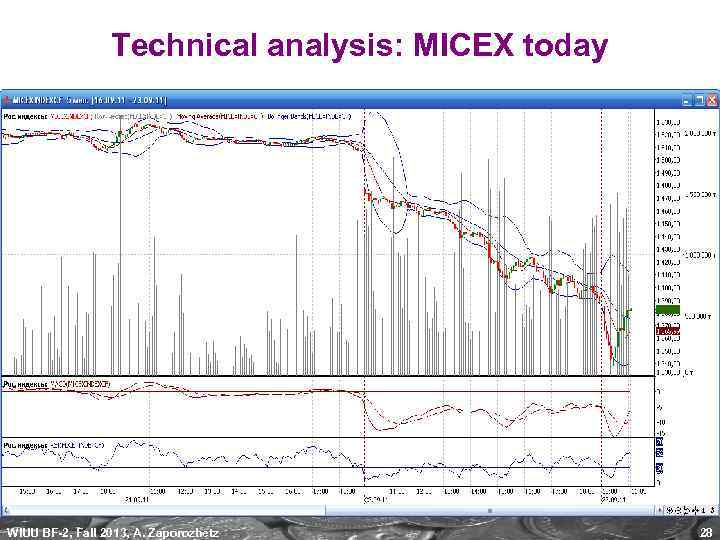Technical analysis: MICEX today WIUU BF-2, Fall 2013, A. Zaporozhetz 28

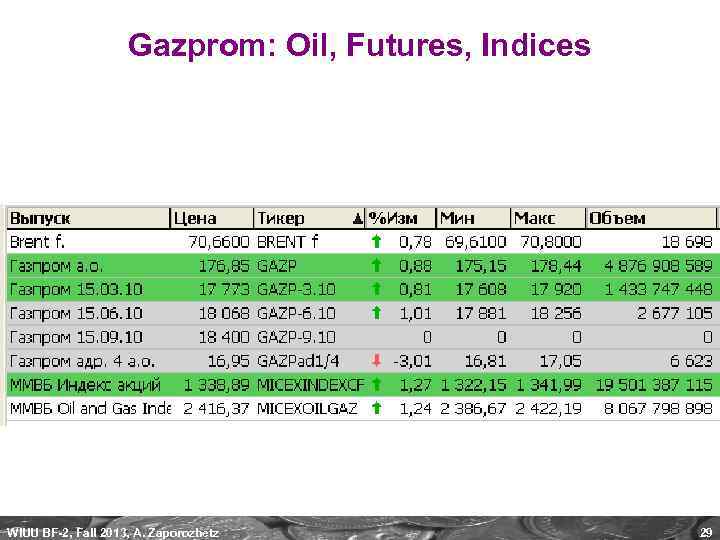Gazprom: Oil, Futures, Indices WIUU BF-2, Fall 2013, A. Zaporozhetz 29

Food for thought: Correlation of PZLT ( «Полюс золото» ) in 2010 with: Market (RTSI): 0, 43 Competitor (“Polimetall”): 0, 49 Gold (LME): 0, 52 WIUU BF-2, Fall 2013, A. Zaporozhetz 30

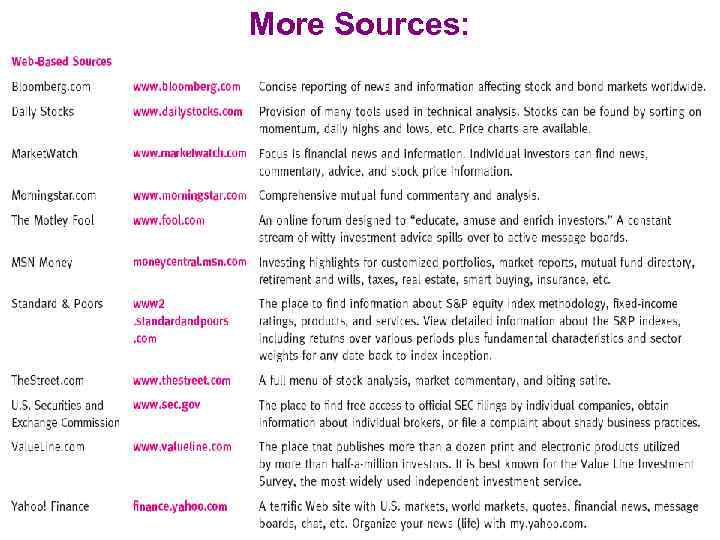More Sources: WIUU BF-2, Fall 2013, A. Zaporozhetz 31

Class 2 Portfolio MGT Additional materials WIUU BF-2, Fall 2013, A. Zaporozhetz 32

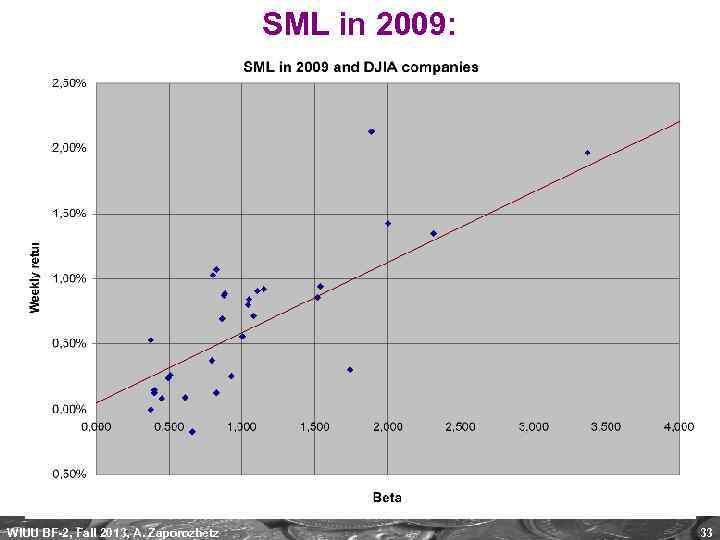SML in 2009: WIUU BF-2, Fall 2013, A. Zaporozhetz 33

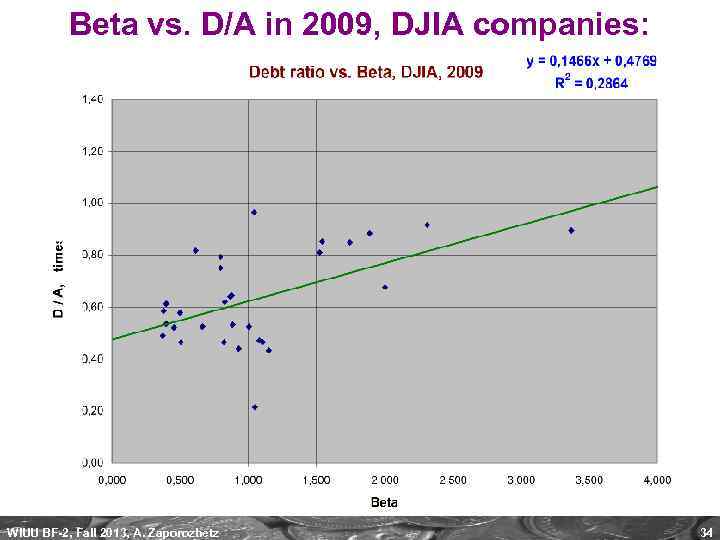Beta vs. D/A in 2009, DJIA companies: WIUU BF-2, Fall 2013, A. Zaporozhetz 34

“CV curse” © A. Zaporozhetz According to the CV rule, we need to chose the lowest CV securities. The risk-free US T-bills/notes have the lowest CV, too, as their sigma is MIN. 1. BUT do we like those returns? Therefore, the CV rule may be misleading. 2. The securities on the CML have NOT the same CVs. We need to design some other portfolio MGT ratios to adjust for the risk-free factor, to overcome the “CV curse”, e. g. , Sharpe’s, Treynor’s… WIUU BF-2, Fall 2013, A. Zaporozhetz 35

Correlation is a measure of the linear association between the 2 variables. In the world of finance, a statistical measure of how two securities move in relation to each other. ρ 1, 2 = Cov 1, 2 / σ 1 σ 2 Correlation coefficient is ALWAYS [-1; 1]. Perfect positive correlation (a correlation coefficient of +1) implies that as one security moves, either up or down, the other security will move in lockstep, in the same direction. Alternatively, perfect negative correlation means that if one security moves in either direction the security that is perfectly negatively correlated will move by an equal amount in the opposite direction. If the correlation is 0, the movements of the securities are said to have no correlation; they are completely random. WIUU BF-2, Fall 2013, A. Zaporozhetz 36