Cистема исчислений Подготовил ст. преподаватель Дихамбеков Ж.












03_sistema_ischisleniy.pptx
- Размер: 54.4 Мб
- Автор: Бекзат Рахманов
- Количество слайдов: 13
Описание презентации Cистема исчислений Подготовил ст. преподаватель Дихамбеков Ж. по слайдам
 Cистема исчислений Подготовил ст. преподаватель Дихамбеков Ж. К. Государственный медицинский университет города Семей 2013 год. Закройте окно «Мастера активации Microsoft office» . Нажмите функциональную клавишу F 5. Если Вы достаточно хорошо просмотрели слайд, то после появления текста « Переход на следующий слайд производится щелчком мыши» щелкните мышью, но можно и подождать чтобы поглубже вникнуть. Если хотите повторить просмотр слайда со звуком, то после появления текста « Переход на следующий слайд производится щелчком мыши» нужно щелкнуть правой кнопкой мыши и выбрать команду «Назад» . Переход на следующий слайд производится щелчком мыши
Cистема исчислений Подготовил ст. преподаватель Дихамбеков Ж. К. Государственный медицинский университет города Семей 2013 год. Закройте окно «Мастера активации Microsoft office» . Нажмите функциональную клавишу F 5. Если Вы достаточно хорошо просмотрели слайд, то после появления текста « Переход на следующий слайд производится щелчком мыши» щелкните мышью, но можно и подождать чтобы поглубже вникнуть. Если хотите повторить просмотр слайда со звуком, то после появления текста « Переход на следующий слайд производится щелчком мыши» нужно щелкнуть правой кнопкой мыши и выбрать команду «Назад» . Переход на следующий слайд производится щелчком мыши
 Вычитание чисел двоичной системы. Сложение чисел двоичной системы. Нахождение десятичного эквивалента числа двоичной системы Нахождение двоичного эквивалента числа десятичной системы. Первые 32 числа в различных системах исчислений. Виды систем исчислений Системы исчислений. Двоичная система исчислений. Умножение и деление чисел двоичной системы. Введение Заключение Перевод числа десятичной системы в число восьмеричной и шестнадцатеричной системы Переход на следующий слайд производится щелчком мыши
Вычитание чисел двоичной системы. Сложение чисел двоичной системы. Нахождение десятичного эквивалента числа двоичной системы Нахождение двоичного эквивалента числа десятичной системы. Первые 32 числа в различных системах исчислений. Виды систем исчислений Системы исчислений. Двоичная система исчислений. Умножение и деление чисел двоичной системы. Введение Заключение Перевод числа десятичной системы в число восьмеричной и шестнадцатеричной системы Переход на следующий слайд производится щелчком мыши
 Введение Как известно электронно-вычислительные устройства, куда входят и компьютеры, работают с информацией, представленной в двоичных кодах, т. е. последовательностью нулей и единиц. Такие числа называются числами двоичного исчисления. Системой исчисления называют совокупность правил и методов представления чисел в виде специальных символов, в том числе цифр. Системы исчисления разделяются на два вида: не позиционный и позиционный. В не позиционной системе значение символа не зависит от его расположения в составе числа. К такой системе относится римское исчисление. Например, обычное число 50 римским исчислением представляется в виде ХХХХХ, где Х обозначает привычном нам исчислении число 10, поэтому 5 десятков есть 50. В позиционных системах значение символа зависит от его позиции в составе числа. К такой системе относится привычное нам десятеричное исчисление. Например, в числе 555 последняя цифра имеет, значение 5, а средняя цифра 5 – 50 и первая цифра 5 – 500. В настоящее время пользуются следующими видами исчисления: двоичный, восьмеричный, десятеричный и шестнадцатеричный. Все эти исчисления являются позиционными. В каждой из этих систем основанием являются числа определяющие их названия: 2, 8, 10 и 16. Из этих систем исчисления двоичная система является основной в электронно-вычислительных устройствах. Восьмеричная и шестнадцатеричная системы являются дополнительными. Для нас привычна десятеричная система исчислении и вычислительные устройства числа, представленные в этой системе, переводить в двоичные, затем применяют к ним математическое действие. Результат переводит в число десятичной системы и выдает на экран. Такие же действия производятся и с текстовыми символами. Рассмотрим действия выполняемые в вычислительных системах с числами. Переход на следующий слайд производится щелчком мыши
Введение Как известно электронно-вычислительные устройства, куда входят и компьютеры, работают с информацией, представленной в двоичных кодах, т. е. последовательностью нулей и единиц. Такие числа называются числами двоичного исчисления. Системой исчисления называют совокупность правил и методов представления чисел в виде специальных символов, в том числе цифр. Системы исчисления разделяются на два вида: не позиционный и позиционный. В не позиционной системе значение символа не зависит от его расположения в составе числа. К такой системе относится римское исчисление. Например, обычное число 50 римским исчислением представляется в виде ХХХХХ, где Х обозначает привычном нам исчислении число 10, поэтому 5 десятков есть 50. В позиционных системах значение символа зависит от его позиции в составе числа. К такой системе относится привычное нам десятеричное исчисление. Например, в числе 555 последняя цифра имеет, значение 5, а средняя цифра 5 – 50 и первая цифра 5 – 500. В настоящее время пользуются следующими видами исчисления: двоичный, восьмеричный, десятеричный и шестнадцатеричный. Все эти исчисления являются позиционными. В каждой из этих систем основанием являются числа определяющие их названия: 2, 8, 10 и 16. Из этих систем исчисления двоичная система является основной в электронно-вычислительных устройствах. Восьмеричная и шестнадцатеричная системы являются дополнительными. Для нас привычна десятеричная система исчислении и вычислительные устройства числа, представленные в этой системе, переводить в двоичные, затем применяют к ним математическое действие. Результат переводит в число десятичной системы и выдает на экран. Такие же действия производятся и с текстовыми символами. Рассмотрим действия выполняемые в вычислительных системах с числами. Переход на следующий слайд производится щелчком мыши
 В десятичной системе исчислений (в системе исчислений применяемой нами ежедневно) для обозначения числа используются 10 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Например: число сорок три целых восемдесять две сотых в десятичной системе будет 43, 82 В двоичной системе исчислений для обозначения числа используются две арабские цифры: 0 и 1 Например: число сорок три целых восемдесять две сотых в двоичной системе будет ≈ 101011, 11011 В восьмеричной системе исчислений для обозначения числа используются 8 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7 Например: число сорок три целых восемдесять две сотых в восьмеричной системе будет ≈ 53, 64365 В шестнадцатеричной системе исчислений для обозначения числа используются 10 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и 6 латинских букв A, B, C, D, E, F Например: число сорок три целых восемдесять две сотых в шестнадцатеричной системе будет ≈ 2 B, D 05 B 7 Виды систем исчислений Систему исчисления числа принято указывать в виде индекса числа: 43, 82 10 ≈ 101011, 11011 2 ≈ 53, 64365 8 ≈ 2 B, D 05 B 7 16 Переход на следующий слайд производится щелчком мыши
В десятичной системе исчислений (в системе исчислений применяемой нами ежедневно) для обозначения числа используются 10 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Например: число сорок три целых восемдесять две сотых в десятичной системе будет 43, 82 В двоичной системе исчислений для обозначения числа используются две арабские цифры: 0 и 1 Например: число сорок три целых восемдесять две сотых в двоичной системе будет ≈ 101011, 11011 В восьмеричной системе исчислений для обозначения числа используются 8 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7 Например: число сорок три целых восемдесять две сотых в восьмеричной системе будет ≈ 53, 64365 В шестнадцатеричной системе исчислений для обозначения числа используются 10 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и 6 латинских букв A, B, C, D, E, F Например: число сорок три целых восемдесять две сотых в шестнадцатеричной системе будет ≈ 2 B, D 05 B 7 Виды систем исчислений Систему исчисления числа принято указывать в виде индекса числа: 43, 82 10 ≈ 101011, 11011 2 ≈ 53, 64365 8 ≈ 2 B, D 05 B 7 16 Переход на следующий слайд производится щелчком мыши
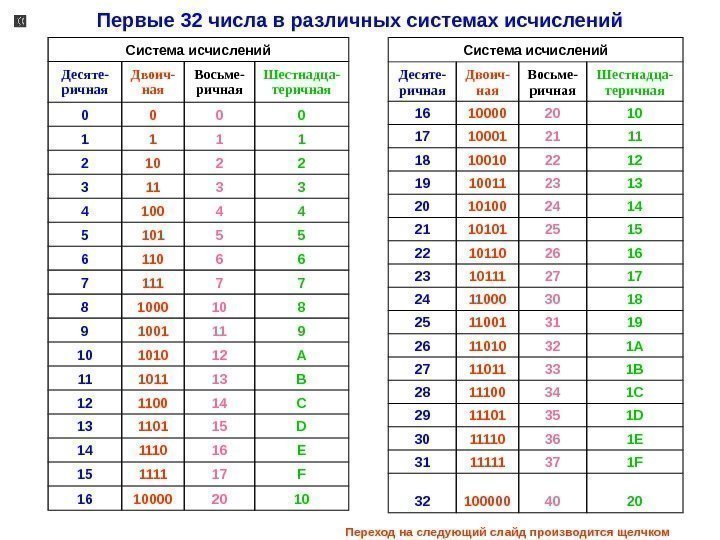
 Система исчислений Десяте- ричная Двоич- ная Восьме- ричная Шестнадца- теричная 0 0 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 Система исчислений Десяте- ричная Двоич- ная Восьме- ричная Шестнадца- теричная 16 10000 20 10 17 10001 21 11 18 10010 22 12 19 10011 23 13 20 10100 24 14 21 10101 25 15 22 10110 26 16 23 10111 27 17 24 11000 30 18 25 11001 31 19 26 11010 32 1 A 27 11011 33 1 B 28 11100 34 1 C 29 11101 35 1 D 30 11110 36 1 E 31 11111 37 1 F 32 100000 40 20 Первые 32 числа в различных системах исчислений Переход на следующий слайд производится щелчком мыши
Система исчислений Десяте- ричная Двоич- ная Восьме- ричная Шестнадца- теричная 0 0 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 Система исчислений Десяте- ричная Двоич- ная Восьме- ричная Шестнадца- теричная 16 10000 20 10 17 10001 21 11 18 10010 22 12 19 10011 23 13 20 10100 24 14 21 10101 25 15 22 10110 26 16 23 10111 27 17 24 11000 30 18 25 11001 31 19 26 11010 32 1 A 27 11011 33 1 B 28 11100 34 1 C 29 11101 35 1 D 30 11110 36 1 E 31 11111 37 1 F 32 100000 40 20 Первые 32 числа в различных системах исчислений Переход на следующий слайд производится щелчком мыши
 1) Результат деления числа 357 на 2 с точностью до целых будет 178 и остается остаток 1 (показан красным цветом) 2) Результат деления числа 178 на 2 с точностью до целых будет 89 и остатка не будет, поэтому пишется 0 (показан красным цветом) 3) Результат деления числа 89 на 2 с точностью до целых будет 44 и остается остаток 1 (показан красным цветом) 4) Результат деления числа 44 на 2 с точностью до целых будет 22 и остатка не будет, поэтому пишется 0 (показан красным цветом) 5) Результат деления числа 22 на 2 с точностью до целых будет 11 и остатка не будет, поэтому пишется 0 (показан красным цветом) 6) Результат деления числа 11 на 2 с точностью до целых будет 5 и остается остаток 1 (показан красным цветом) 7) Результат деления числа 5 на 2 с точностью до целых будет 2 и остается остаток 1 (показан красным цветом) 8) Результат деления числа 2 на 2 с точностью до целых будет 1 и остатка не будет, поэтому пишется 0 (показан красным цветом) 9) Результат деления числа 1 на 2 с точностью до целых будет 0 и остается остаток 1 (показан красным цветом) Перевод числа 357, 79 десятичной системы исчисления в число двоичной системы Последней операцией деления обязательно должно быть деление 1 на 2, т. е. частное должно равняться 0, а остаток 1. 357 10 = 101100101 2 можно осуществить путем деления целой части на 2 и умножением на 2 дробной части За двоичный экви-валент принимается последовательность остатков с послед-него к начальному, т. е. снизу вверх. Для нахождения двоичного эквивалента дробной части десятичного числа только дробная часть числа умножается на 2. 1) Произведение 0, 79 на 2 будет 1, 58. Целые части чисел 0, 79 и 1, 58 написать отдельно (выделено красным цветом) 2) Произведение на 2 дробной части 0, 58 полученного результата (1, 58) даст 1, 16. Написать отдельно целую часть этого числа (выделено красным цветом) 3) Произведение на 2 дробной части 0, 16 полученного результата (1, 16) даст 0, 32. Написать отдельно целую часть этого числа (выделено красным цветом). 4) Произведение на 2 дробной части 0, 32 полученного результата (0, 32) даст 0, 64. Написать отдельно целую часть этого числа (выделено красным цветом). 5) Произведение на 2 дробной части 0, 64 полученного результата (0, 64) даст 1, 28. Написать отдельно целую часть этого числа (выделено красным цветом). При этом обязательно должна быть известна точность задания двоичного эквивалента, т. е. число знаков после запятой. При умножении целые части чисел выделяются, так как они и образуют двоичный эквивалент. При нахождении двоичного эквивалента с 5 -тью знаками после запятой для десятичного числа 0, 79 выполняются действия: 0, 79 10 = 0, 11001 2 357, 79 10 = 101100101, 11001 2 Последовательность целых, взятых с начального к последнему, т. е. сверху вниз, образует двоичный эквивалент дробной части десятичного числа. Нахождение двоичного эквивалента числа десятичной системы Переход на следующий слайд производится щелчком мыши
1) Результат деления числа 357 на 2 с точностью до целых будет 178 и остается остаток 1 (показан красным цветом) 2) Результат деления числа 178 на 2 с точностью до целых будет 89 и остатка не будет, поэтому пишется 0 (показан красным цветом) 3) Результат деления числа 89 на 2 с точностью до целых будет 44 и остается остаток 1 (показан красным цветом) 4) Результат деления числа 44 на 2 с точностью до целых будет 22 и остатка не будет, поэтому пишется 0 (показан красным цветом) 5) Результат деления числа 22 на 2 с точностью до целых будет 11 и остатка не будет, поэтому пишется 0 (показан красным цветом) 6) Результат деления числа 11 на 2 с точностью до целых будет 5 и остается остаток 1 (показан красным цветом) 7) Результат деления числа 5 на 2 с точностью до целых будет 2 и остается остаток 1 (показан красным цветом) 8) Результат деления числа 2 на 2 с точностью до целых будет 1 и остатка не будет, поэтому пишется 0 (показан красным цветом) 9) Результат деления числа 1 на 2 с точностью до целых будет 0 и остается остаток 1 (показан красным цветом) Перевод числа 357, 79 десятичной системы исчисления в число двоичной системы Последней операцией деления обязательно должно быть деление 1 на 2, т. е. частное должно равняться 0, а остаток 1. 357 10 = 101100101 2 можно осуществить путем деления целой части на 2 и умножением на 2 дробной части За двоичный экви-валент принимается последовательность остатков с послед-него к начальному, т. е. снизу вверх. Для нахождения двоичного эквивалента дробной части десятичного числа только дробная часть числа умножается на 2. 1) Произведение 0, 79 на 2 будет 1, 58. Целые части чисел 0, 79 и 1, 58 написать отдельно (выделено красным цветом) 2) Произведение на 2 дробной части 0, 58 полученного результата (1, 58) даст 1, 16. Написать отдельно целую часть этого числа (выделено красным цветом) 3) Произведение на 2 дробной части 0, 16 полученного результата (1, 16) даст 0, 32. Написать отдельно целую часть этого числа (выделено красным цветом). 4) Произведение на 2 дробной части 0, 32 полученного результата (0, 32) даст 0, 64. Написать отдельно целую часть этого числа (выделено красным цветом). 5) Произведение на 2 дробной части 0, 64 полученного результата (0, 64) даст 1, 28. Написать отдельно целую часть этого числа (выделено красным цветом). При этом обязательно должна быть известна точность задания двоичного эквивалента, т. е. число знаков после запятой. При умножении целые части чисел выделяются, так как они и образуют двоичный эквивалент. При нахождении двоичного эквивалента с 5 -тью знаками после запятой для десятичного числа 0, 79 выполняются действия: 0, 79 10 = 0, 11001 2 357, 79 10 = 101100101, 11001 2 Последовательность целых, взятых с начального к последнему, т. е. сверху вниз, образует двоичный эквивалент дробной части десятичного числа. Нахождение двоичного эквивалента числа десятичной системы Переход на следующий слайд производится щелчком мыши
 101100101, 11001 2 Разряд. При определении десятичного эквивалента двоичного числа 101100101, 11001 каждой цифре (нулю и единице) этого числа дается разряд в виде целого числа. Цифре перед запятой дается разряд равный нулю и разряд влево увеличивается, а вправо уменьшается. Для целой части разряд положительное число, для дробной части — отрицательное число: Сумма произведений каждой цифры двоичного числа на два в степени равной разряду этой цифры дает десятичный эквивалент этого числа: 1*2 8 = 256 + 0 + 64 + 32 + 0 + 4 + 0 + 1 + 0, 5 + 0, 25 + 0 + 0, 03125 = = 357, 78125 n 8 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 2 n 256 128 64 32 16 8 4 2 1 0, 5 0, 25 0, 125 0, 0625 0, 03125 Значения числа 2 в степени n, используемых при данном вычислении. Число 101100101, 11001 2 было ранее установлено как двоичный эквивалент десятичного числа 357, 79 10. При обратном переводе определяется, что двоичный эквивалент является числом приближенным (равным или меньшим) числу в десятичной системе исчисления. Нахождение десятичного эквивалента числа двоичной системы 8 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 +0*2 7 +1*2 6 +1*2 5 +0*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 +1*2 -1 +1*2 -2 +0*2 -3 +0*2 -4 +1*2 -5 = ≈ 357, 79 Переход на следующий слайд производится щелчком мыши
101100101, 11001 2 Разряд. При определении десятичного эквивалента двоичного числа 101100101, 11001 каждой цифре (нулю и единице) этого числа дается разряд в виде целого числа. Цифре перед запятой дается разряд равный нулю и разряд влево увеличивается, а вправо уменьшается. Для целой части разряд положительное число, для дробной части — отрицательное число: Сумма произведений каждой цифры двоичного числа на два в степени равной разряду этой цифры дает десятичный эквивалент этого числа: 1*2 8 = 256 + 0 + 64 + 32 + 0 + 4 + 0 + 1 + 0, 5 + 0, 25 + 0 + 0, 03125 = = 357, 78125 n 8 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 2 n 256 128 64 32 16 8 4 2 1 0, 5 0, 25 0, 125 0, 0625 0, 03125 Значения числа 2 в степени n, используемых при данном вычислении. Число 101100101, 11001 2 было ранее установлено как двоичный эквивалент десятичного числа 357, 79 10. При обратном переводе определяется, что двоичный эквивалент является числом приближенным (равным или меньшим) числу в десятичной системе исчисления. Нахождение десятичного эквивалента числа двоичной системы 8 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 +0*2 7 +1*2 6 +1*2 5 +0*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 +1*2 -1 +1*2 -2 +0*2 -3 +0*2 -4 +1*2 -5 = ≈ 357, 79 Переход на следующий слайд производится щелчком мыши
 1 0 1 1 0 0 1 1 , 1 0 1 + 1 0 1 1 0 , 0 1 1 1 0 При сложении чисел в двоичной системе исчисления нужно помнить следующие правила : 1) 0 + 0 = 0 2) 0 + 1 = 1 3) 1 + 0 = 1 4) 1 + 1 = 10 Сложение двоичных чисел 10110011, 10101 и 10110, 01110 Эти числа надо написать так, чтобы знаки дроби “запятая” были расположены друг под другом. Сложение производится справа налево для цифр с одинаковыми разрядами. Цифре слева от запятой присваивается разряд нуль (0). Влево от запятой разряд возрастает (знак положителен), вправо от запятой разряд убывает (знак отрицателен). Результат сложения цифр 1 и 0 с разрядом -5 равен 1 (правило 3). Результат сложения цифр 0 и 1 с разрядом -4 равен 1 (правило 2). Результат сложения цифр 1 и 1 с разрядом -3 равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 и 1 с разрядом -2 (и 1 в памяти) равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 1 и 0 с разрядом -1 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 1 и 0 с разрядом 0 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). 5) 1 + 1 = 11 Результат сложения цифр 1 и 1 с разрядом 1 и 1 в памяти равен 11 (правило 5). 1 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 и 1 с разрядом 2 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 и 0 с разрядом 3 и 1 в памяти равен 1 (правило 2). 1 пишется как результат. Результат сложения цифр 1 и 1 с разрядом 4 равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 1 с разрядом 5 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 с разрядом 6 и 1 в памяти равен 1 (правило 2). 1 пишется как результат. Нет цифры которую нужно сложить с 1 разрядом 7, поэтому 1 записывается как результат. 7 6 5 4 3 2 1 0 Сложение чисел двоичной системы -1 -2 -3 -4 -5 Переход на следующий слайд производится щелчком мыши
1 0 1 1 0 0 1 1 , 1 0 1 + 1 0 1 1 0 , 0 1 1 1 0 При сложении чисел в двоичной системе исчисления нужно помнить следующие правила : 1) 0 + 0 = 0 2) 0 + 1 = 1 3) 1 + 0 = 1 4) 1 + 1 = 10 Сложение двоичных чисел 10110011, 10101 и 10110, 01110 Эти числа надо написать так, чтобы знаки дроби “запятая” были расположены друг под другом. Сложение производится справа налево для цифр с одинаковыми разрядами. Цифре слева от запятой присваивается разряд нуль (0). Влево от запятой разряд возрастает (знак положителен), вправо от запятой разряд убывает (знак отрицателен). Результат сложения цифр 1 и 0 с разрядом -5 равен 1 (правило 3). Результат сложения цифр 0 и 1 с разрядом -4 равен 1 (правило 2). Результат сложения цифр 1 и 1 с разрядом -3 равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 и 1 с разрядом -2 (и 1 в памяти) равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 1 и 0 с разрядом -1 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 1 и 0 с разрядом 0 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). 5) 1 + 1 = 11 Результат сложения цифр 1 и 1 с разрядом 1 и 1 в памяти равен 11 (правило 5). 1 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 и 1 с разрядом 2 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 и 0 с разрядом 3 и 1 в памяти равен 1 (правило 2). 1 пишется как результат. Результат сложения цифр 1 и 1 с разрядом 4 равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 1 с разрядом 5 и 1 в памяти равен 10 (правило 4). 0 пишется как результат, а 1 сохраняется в памяти для сложения с цифрами следующего разряда (показано красным цветом). Результат сложения цифр 0 с разрядом 6 и 1 в памяти равен 1 (правило 2). 1 пишется как результат. Нет цифры которую нужно сложить с 1 разрядом 7, поэтому 1 записывается как результат. 7 6 5 4 3 2 1 0 Сложение чисел двоичной системы -1 -2 -3 -4 -5 Переход на следующий слайд производится щелчком мыши
 При вычитании чисел в двоичной системе исчисления нужно помнить следующие правила: 2) 1 — 0 = 1 3) 1 — 1 = 0 4) 10 — 1 = 1 Вычитание двоичных чисел от 1010011, 10101 числа 11110, 11110 Эти числа надо написать так, чтобы знак дроби “запятая” были расположены друг под другом. Вычитание производится справа налево для цифр с одинаковыми разрядами. Цифре слева от запятой присваивается разряд нуль (0). Влево от него разряд возрастает (знак положителен), вправо от него разряд убывает (знак отрицателен). Результат вычитания 0 -я от 1 цифр с разрядами -5 равен 1 (правило 2). При вычитании 1 от 0 (чисел с разрядом -4) нужно в вычитаемом занять 1 от числа с разрядом -3, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом -4 будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) При вычитании 1 от 0 (чисел с разрядом -3) нужно в уменьшаемом занять 1 от числа с разрядом -1, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом -2 будет 10, здесь останется 1, так как от него занимается 1 для цифры разрядом -3, где будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) Результат вычитания 1 от 1 цифр с разрядами -2 равен 0 (правило 3). При вычитании 1 от 0 (чисел с разрядом -1) нужно в уменьшаемом занять 1 от числа с разрядом 0, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом -1 будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) Результат вычитания 0 от 0 цифр с разрядами 0 равен 0 (правило 1). Результат вычитания 1 от 1 цифр с разрядами 1 равен 0 (правило 3). При вычитании 1 от 0 (чисел с разрядом 2) нужно в уменьшаемом занять 1 от числа с разрядом 4, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом 3 будет 10, здесь останется 1, так как от него занимается 1 для цифры разрядом 2, где будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) Результат вычитания 1 от 1 цифр с разрядами 3 равен 0 (правило 3). При вычитании 1 от 0 (чисел с разрядом 4) нужно в уменьшаемом занять 1 от числа с разрядом 6, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом 5 будет 10, здесь останется 1, так как от него занимается 1 для цифры разрядом 4, где будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) В цифрах 5 -го разряда нет вычитаемого от 1 поэтому в результат вычитания записывается 1. Вычитание чисел двоичной системы 1) 0 — 0 = 0 Разряд 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 Переход на следующий слайд производится щелчком мыши
При вычитании чисел в двоичной системе исчисления нужно помнить следующие правила: 2) 1 — 0 = 1 3) 1 — 1 = 0 4) 10 — 1 = 1 Вычитание двоичных чисел от 1010011, 10101 числа 11110, 11110 Эти числа надо написать так, чтобы знак дроби “запятая” были расположены друг под другом. Вычитание производится справа налево для цифр с одинаковыми разрядами. Цифре слева от запятой присваивается разряд нуль (0). Влево от него разряд возрастает (знак положителен), вправо от него разряд убывает (знак отрицателен). Результат вычитания 0 -я от 1 цифр с разрядами -5 равен 1 (правило 2). При вычитании 1 от 0 (чисел с разрядом -4) нужно в вычитаемом занять 1 от числа с разрядом -3, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом -4 будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) При вычитании 1 от 0 (чисел с разрядом -3) нужно в уменьшаемом занять 1 от числа с разрядом -1, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом -2 будет 10, здесь останется 1, так как от него занимается 1 для цифры разрядом -3, где будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) Результат вычитания 1 от 1 цифр с разрядами -2 равен 0 (правило 3). При вычитании 1 от 0 (чисел с разрядом -1) нужно в уменьшаемом занять 1 от числа с разрядом 0, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом -1 будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) Результат вычитания 0 от 0 цифр с разрядами 0 равен 0 (правило 1). Результат вычитания 1 от 1 цифр с разрядами 1 равен 0 (правило 3). При вычитании 1 от 0 (чисел с разрядом 2) нужно в уменьшаемом занять 1 от числа с разрядом 4, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом 3 будет 10, здесь останется 1, так как от него занимается 1 для цифры разрядом 2, где будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) Результат вычитания 1 от 1 цифр с разрядами 3 равен 0 (правило 3). При вычитании 1 от 0 (чисел с разрядом 4) нужно в уменьшаемом занять 1 от числа с разрядом 6, где останется 0. Тогда в уменьшаемом вместо цифры 0 с разрядом 5 будет 10, здесь останется 1, так как от него занимается 1 для цифры разрядом 4, где будет 10 (показано красным цветом) и вычитание от него 1 даст результат 1 (правило 4) В цифрах 5 -го разряда нет вычитаемого от 1 поэтому в результат вычитания записывается 1. Вычитание чисел двоичной системы 1) 0 — 0 = 0 Разряд 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 Переход на следующий слайд производится щелчком мыши
 В двоичной системе исчисления при выполнений действии умножения нужно помнить следующие положения : 4) 1 * 1 = 1 1) 0 * 0 = 0 2) 0 * 1 = 0 3) 1 * 0 = 0 Умножение чисел двоичной системы исчисления производятся по привычным правилам десятичной системы исчисления. В двоичной системе исчисления при выполнений действии деления нужно помнить следующие положения : 8) 1 + 1 = 10 5) 0 + 0 = 0 6) 0 + 1 = 1 7) 1 + 0 = 1 4) 1 * 1 = 1 1) 0 * 0 = 0 3) 1 * 0 = 0 8) 10 — 1 = 1 5) 0 — 0 = 0 7) 1 — 1 = 0 2) 0 * 1 = 0 6) 1 — 0 = 1 1 1 0 0 1 1, 1 0 1 * 1 1 0, 1 0 1 Если разряд множителя увеличивается на единицу, то произведение смещается на одно место влево Количество цифр после запятой в результате произведения равно сумме количеств цифр после запятой у обоих множителей 1 1 0 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 1 Деление чисел двоичной системы исчисления производятся по привычным правилам десятичной системы исчисления. Запятая у делимого сдвигается вправо на столько мест на сколько сдвигается запятая у делителя, чтобы он стал целым числом Деление можно продолжать дальше мы посчитали достаточным точность до пяти знаков после запятой. Умножение 110011, 101 2 и 110, 101 2 Деление 110010, 101 2 на 101, 011 2 Умножение и деление чисел двоичной системы Множимое Множитель 1 00000 011010101 Красным цветом указывается число в памяти, которое нужно прибавить к следующему разряду слагаемых Переход на следующий слайд производится щелчком мыши
В двоичной системе исчисления при выполнений действии умножения нужно помнить следующие положения : 4) 1 * 1 = 1 1) 0 * 0 = 0 2) 0 * 1 = 0 3) 1 * 0 = 0 Умножение чисел двоичной системы исчисления производятся по привычным правилам десятичной системы исчисления. В двоичной системе исчисления при выполнений действии деления нужно помнить следующие положения : 8) 1 + 1 = 10 5) 0 + 0 = 0 6) 0 + 1 = 1 7) 1 + 0 = 1 4) 1 * 1 = 1 1) 0 * 0 = 0 3) 1 * 0 = 0 8) 10 — 1 = 1 5) 0 — 0 = 0 7) 1 — 1 = 0 2) 0 * 1 = 0 6) 1 — 0 = 1 1 1 0 0 1 1, 1 0 1 * 1 1 0, 1 0 1 Если разряд множителя увеличивается на единицу, то произведение смещается на одно место влево Количество цифр после запятой в результате произведения равно сумме количеств цифр после запятой у обоих множителей 1 1 0 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0 1 Деление чисел двоичной системы исчисления производятся по привычным правилам десятичной системы исчисления. Запятая у делимого сдвигается вправо на столько мест на сколько сдвигается запятая у делителя, чтобы он стал целым числом Деление можно продолжать дальше мы посчитали достаточным точность до пяти знаков после запятой. Умножение 110011, 101 2 и 110, 101 2 Деление 110010, 101 2 на 101, 011 2 Умножение и деление чисел двоичной системы Множимое Множитель 1 00000 011010101 Красным цветом указывается число в памяти, которое нужно прибавить к следующему разряду слагаемых Переход на следующий слайд производится щелчком мыши
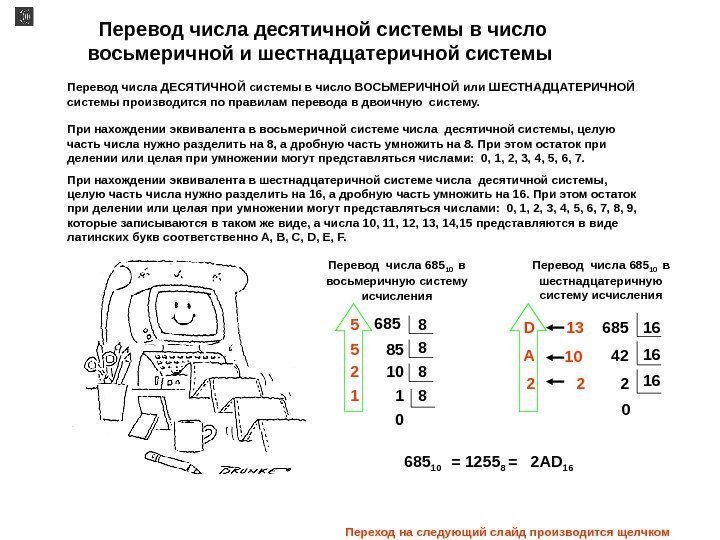
 Перевод числа десятичной системы в число восьмеричной и шестнадцатеричной системы Перевод числа ДЕСЯТИЧНОЙ системы в число ВОСЬМЕРИЧНОЙ или ШЕСТНАДЦАТЕРИЧНОЙ системы производится по правилам перевода в двоичную систему. При нахождении эквивалента в восьмеричной системе числа десятичной системы, целую часть числа нужно разделить на 8, а дробную часть умножить на 8. При этом остаток при делении или целая при умножении могут представляться числами: 0, 1, 2, 3, 4, 5, 6, 7. 85 8 8685 10 1 05 5 2 1 1668513 16 42 10 16 2 2 D A 2 0 685 10 = 1255 8 = 2 AD 16 При нахождении эквивалента в шестнадцатеричной системе числа десятичной системы, целую часть числа нужно разделить на 16, а дробную часть умножить на 16. При этом остаток при делении или целая при умножении могут представляться числами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, которые записываются в таком же виде, а числа 10, 11, 12, 13, 14, 15 представляются в виде латинских букв соответственно A, B, C, D, E, F. Перевод числа 685 10 в восьмеричную систему исчисления Перевод числа 685 10 в шестнадцатеричную систему исчисления Переход на следующий слайд производится щелчком мыши
Перевод числа десятичной системы в число восьмеричной и шестнадцатеричной системы Перевод числа ДЕСЯТИЧНОЙ системы в число ВОСЬМЕРИЧНОЙ или ШЕСТНАДЦАТЕРИЧНОЙ системы производится по правилам перевода в двоичную систему. При нахождении эквивалента в восьмеричной системе числа десятичной системы, целую часть числа нужно разделить на 8, а дробную часть умножить на 8. При этом остаток при делении или целая при умножении могут представляться числами: 0, 1, 2, 3, 4, 5, 6, 7. 85 8 8685 10 1 05 5 2 1 1668513 16 42 10 16 2 2 D A 2 0 685 10 = 1255 8 = 2 AD 16 При нахождении эквивалента в шестнадцатеричной системе числа десятичной системы, целую часть числа нужно разделить на 16, а дробную часть умножить на 16. При этом остаток при делении или целая при умножении могут представляться числами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, которые записываются в таком же виде, а числа 10, 11, 12, 13, 14, 15 представляются в виде латинских букв соответственно A, B, C, D, E, F. Перевод числа 685 10 в восьмеричную систему исчисления Перевод числа 685 10 в шестнадцатеричную систему исчисления Переход на следующий слайд производится щелчком мыши
 Заключение Нахождение эквивалента числа десятичной системы выполняется в три этапа: … Эквивалент в десятичной системе числа другой системы определяется как сумма произведении каждой цифры исходного числа на основание системы исчисления в степени равной разряду этой цифры Первый , целую часть исходного числа нужно делить на основания системы исчисления и продолжить это деление до получения результата деления равной нулю. Остатки деления, взятые с последнего к начальному, есть эквивалент целой части исходного числа. Второй, дробная часть исходного числа умножается на основание системы исчисления и это умножение следует продолжить для дробной части полученного результата до получения точности задания искомого числа. Целые, полученные при умножении и взятые от первого к последнему, есть эквивалент дробной части исходного числа. Причем ноль исходного числа есть целая часть эквивалента. Третий , нахождение искомого эквивалента как сумма этих двух эквивалентов. С числами любой системы исчисления можно проводить все арифметические действия. Шестнадцатеричные числа используются для компактного записи чисел и экономии памяти. Переход на следующий слайд производится щелчком мыши
Заключение Нахождение эквивалента числа десятичной системы выполняется в три этапа: … Эквивалент в десятичной системе числа другой системы определяется как сумма произведении каждой цифры исходного числа на основание системы исчисления в степени равной разряду этой цифры Первый , целую часть исходного числа нужно делить на основания системы исчисления и продолжить это деление до получения результата деления равной нулю. Остатки деления, взятые с последнего к начальному, есть эквивалент целой части исходного числа. Второй, дробная часть исходного числа умножается на основание системы исчисления и это умножение следует продолжить для дробной части полученного результата до получения точности задания искомого числа. Целые, полученные при умножении и взятые от первого к последнему, есть эквивалент дробной части исходного числа. Причем ноль исходного числа есть целая часть эквивалента. Третий , нахождение искомого эквивалента как сумма этих двух эквивалентов. С числами любой системы исчисления можно проводить все арифметические действия. Шестнадцатеричные числа используются для компактного записи чисел и экономии памяти. Переход на следующий слайд производится щелчком мыши
 Спасибо за внимание
Спасибо за внимание

