Цилиндр Опр Цилиндром называется тело полученное при

Цилиндр

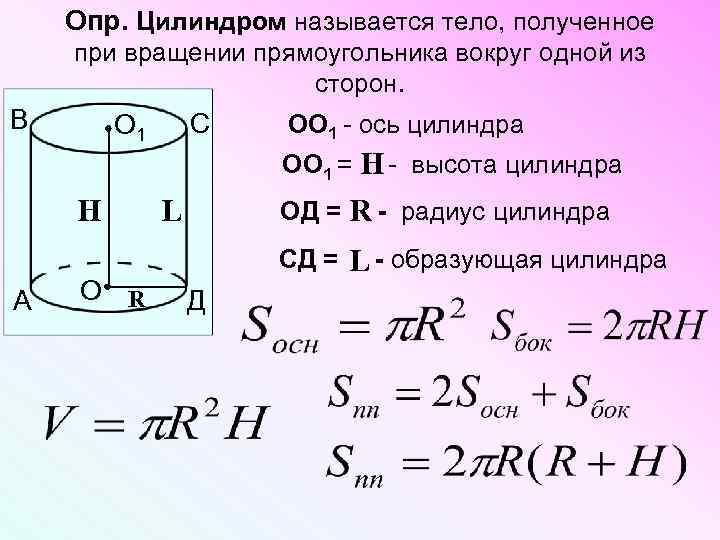Опр. Цилиндром называется тело, полученное при вращении прямоугольника вокруг одной из сторон. В С О 1 OO 1 - ось цилиндра OO 1 = - высота цилиндра Н Н А О R OД = - радиус цилиндра R L СД = - образующая цилиндра L Д

Задача 1. Найдите площадь боковой поверхности цилиндра, диаметр и высота которого равны 4. В С О 1 OД = 2; СД =4 4 А О 2 Дано: АВСД - цилиндр Найти: Sбок Д Решение R = ОД = 2, Н = СД = 4 Ответ: Sбок = 16 кв. ед.

Задача 2. Найдите площадь боковой поверхности В цилиндра, осевое сечение которого – квадрат с площадью, равной 12 см 2. О 1 С Дано: АВСД - цилиндр АВСД - квадрат S АВСД = 12 см 2 О А Д SАВСД = 12 Найти: Sбок Решение R = ОД = , Н = СД = АД = Ответ: Sбок = 12 кв. ед.

Задача 3. Найдите объём р/б цилиндра, площадь осевого сечения которого равна 16. В О 1 С Дано: АВСД – р/б цилиндр S АВСД = 16 см 2 Найти: Vцил О А Д Решение Vцил= 16 см 3

Задача 4. 1. Как изменится боковая поверхность цилиндра, если радиус увеличить в 2 раза ? 2. Как изменится боковая поверхность цилиндра, если высоту увеличить в 2 раза ? 3. Как изменится боковая поверхность цилиндра, если и радиус и высоту увеличить в 3 раза ? 4. Как изменится боковая поверхность цилиндра, если радиус увеличить в 6 раз, а высоту уменьшить в 4 раза ? 5. Как изменится полная поверхность цилиндра, если и радиус и высоту увеличить в 5 раз ? 6. Как изменится объём цилиндра, если радиус увеличить в 2 раза ?

Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. В Дано: АВСД – вписанный О С А цилиндр ОС = 1; СД = 1 Д Найти: Vп/у п/д Решение а=2 Ответ: Vп/у в=2 п/д =4 с=1 куб. ед.

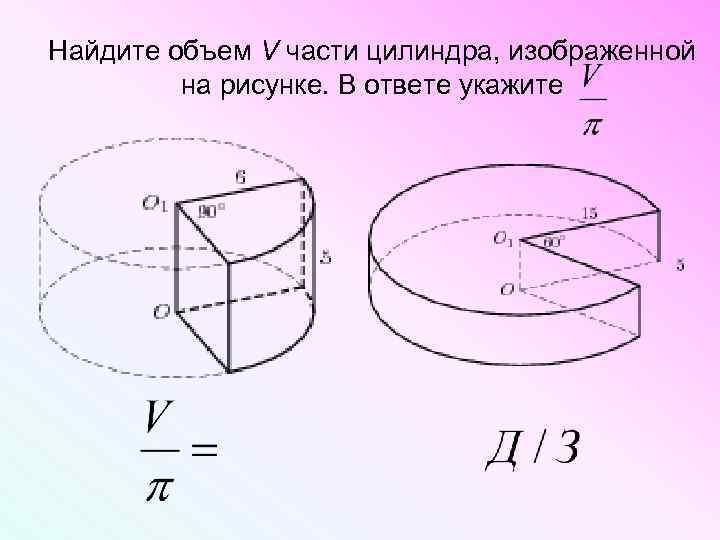Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

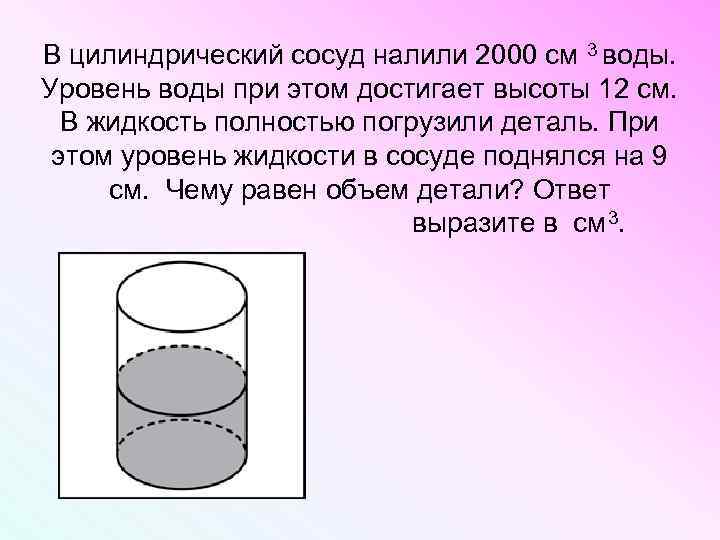В цилиндрический сосуд налили 2000 см 3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см 3.

Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на . В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1, 5 раза. Чему равен объем детали? Ответ выразите в литрах.

Определение. Тело, полученное при вращении п/у треугольника вокруг одного из своих катетов называется конусом ( прямой круговой конус ).

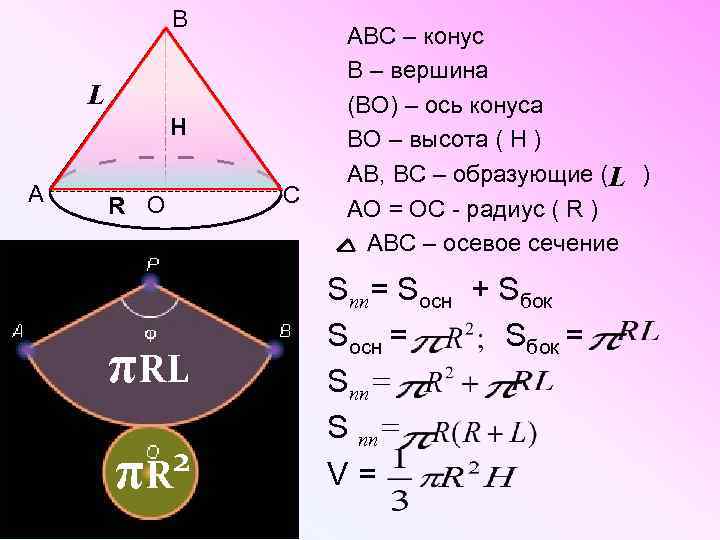В L H А R О πRL 2 πR С АВС – конус В – вершина (ВО) – ось конуса ВО – высота ( Н ) АВ, ВС – образующие ( ) L АО = ОС - радиус ( R ) АВС – осевое сечение Sпп= Sосн + Sбок Sосн = Sбок = Sпп= S пп= V =

са ну ко я Cечения ни че конуса е С Сечения конуса

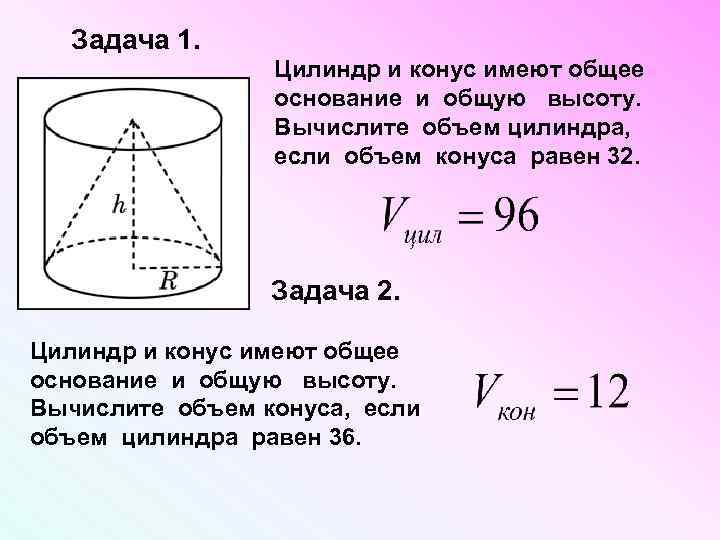Задача 1. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 32. Задача 2. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем конуса, если объем цилиндра равен 36.

Задача 3. 1. Как изменится боковая поверхность и объём конуса, если радиус увеличить в 2 раза 2. Как изменится боковая поверхность и объём конуса, если высоту увеличить в 2 раза ? 3. Как изменится боковая поверхность и объём конуса, если и радиус и высоту увеличить в 2 раза ? 4. Как изменится объём конуса, если радиус увеличить в 2 раза, а высоту уменьшить в 4 раза?

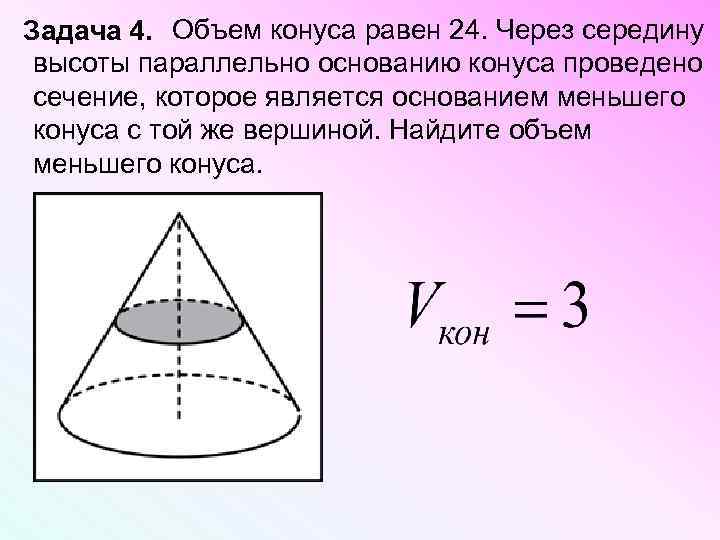Объем конуса равен 24. Через середину Задача 4. высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Задача 5. Объём цилиндра равен 27 см 3. Чему будет равен объём конуса той же высоты и того же основания после увеличения его высоты в 3 раза и уменьшения диаметра в 3 раза ?

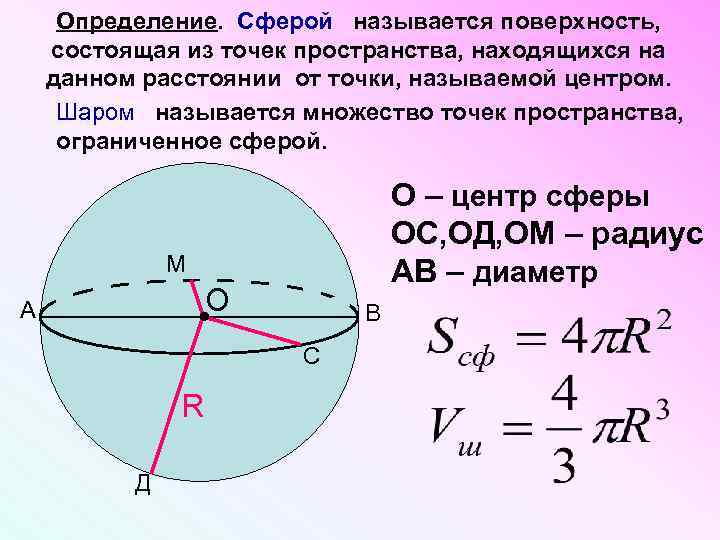Определение. Сферой называется поверхность, состоящая из точек пространства, находящихся на данном расстоянии от точки, называемой центром. Шаром называется множество точек пространства, ограниченное сферой. О – центр cферы ОС, ОД, ОМ – радиус АВ – диаметр М О А В С R Д

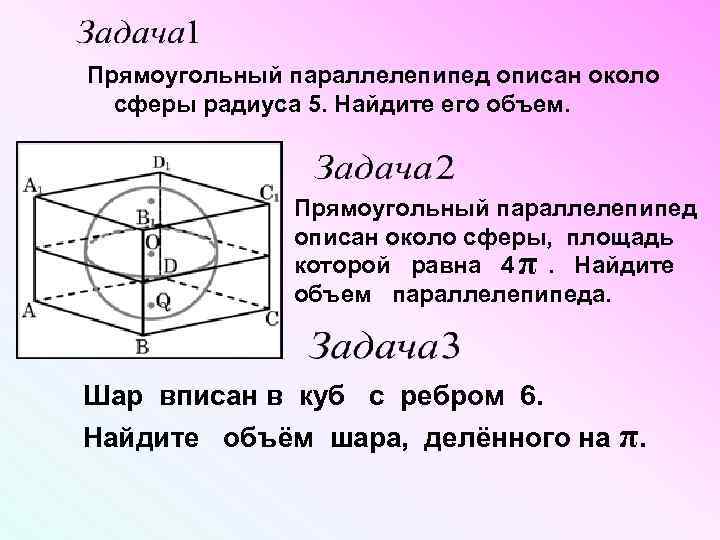Прямоугольный параллелепипед описан около сферы радиуса 5. Найдите его объем. Прямоугольный параллелепипед описан около сферы, площадь которой равна 4 . Найдите π объем параллелепипеда. Шар вписан в куб с ребром 6. Найдите объём шара, делённого на π.

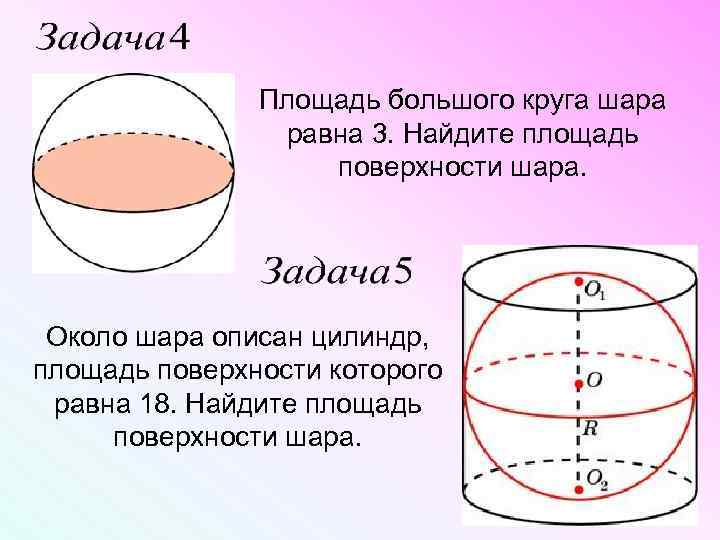Площадь большого круга шара равна 3. Найдите площадь поверхности шара. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

1. Как изменится площадь поверхности и объём шара, если радиус увеличить в 2 раза? В 3 раза? 2. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Цилиндр, описанный около шара.

Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

Около шара, объём которого равен 6, описан цилиндр. Найдите объём цилиндра.

Д/З

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объем параллелепипеда равен 20. Найдите поверхность и объём цилиндра. Площадь поверхности куба равна 24. Найдите поверхность и объём вписанного цилиндра. Объём куба равен 8. Найдите поверхность и объём цилиндра.

. Задача 4. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 4. Боковые рёбра равны . Найдите объём цилиндра, описанного около этой призмы. В А Т К С Задача 5. Объём цилиндра равен 18 см 3. Чему будет равен объём конуса с той же высотой и основанием, если Д высоту увеличить в 2 раза, а радиус уменьшить в 3 раза ? Задача 6. Объем шара равен 288 . Найдите площадь его поверхности, деленную на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на .

Задача № 4 по чертежу Найти радиус окружности, описанной вокруг квадрата АВСД. В С О А 4 Д

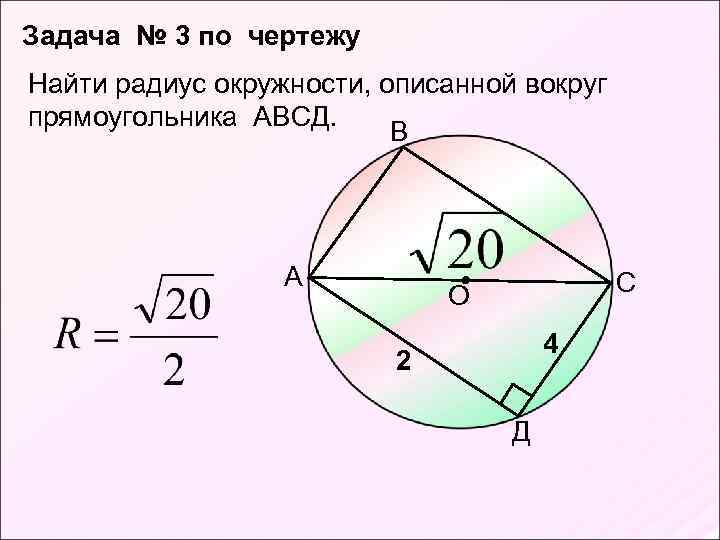Задача № 3 по чертежу Найти радиус окружности, описанной вокруг прямоугольника АВСД. В А С О 4 2 Д

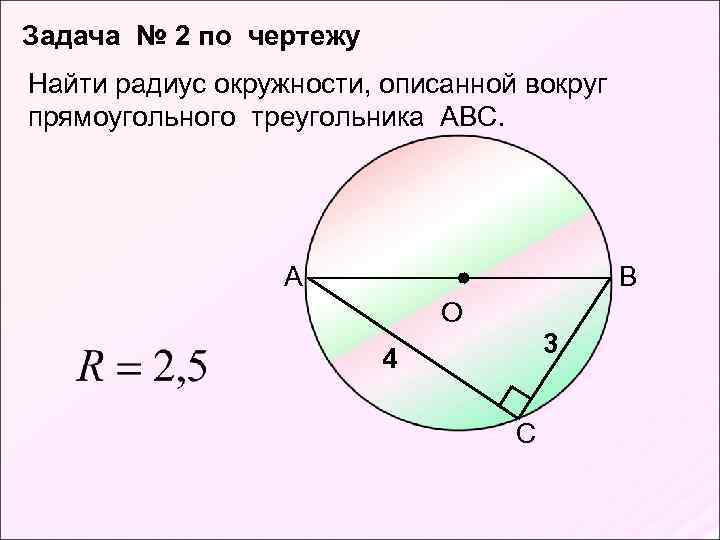Задача № 2 по чертежу Найти радиус окружности, описанной вокруг прямоугольного треугольника АВС. А В О 3 4 С

Задача 6. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые рёбра равны . Найдите объём В цилиндра, описанного около этой призмы. Дано: АВСД – описанный Т С цилиндр АКД – п/у; А АК = 8; КД = 6; СД = К Д Найти: Vцил Решение

Около куба с ребром описан шар. Найдите объем этого шара, деленный на .

Задача 3. Найдите площадь боковой поверхности А О В цилиндра, осевое сечение которого – квадрат с диагональю, равной 12 см. О 1 С Дано: АВСД - цилиндр АВСД - квадрат АС = 12 см АД = СД = АД = Д Найти: Sбок Решение R = ОД = Н = СД = Ответ: Sбок = 36 кв. ед.

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

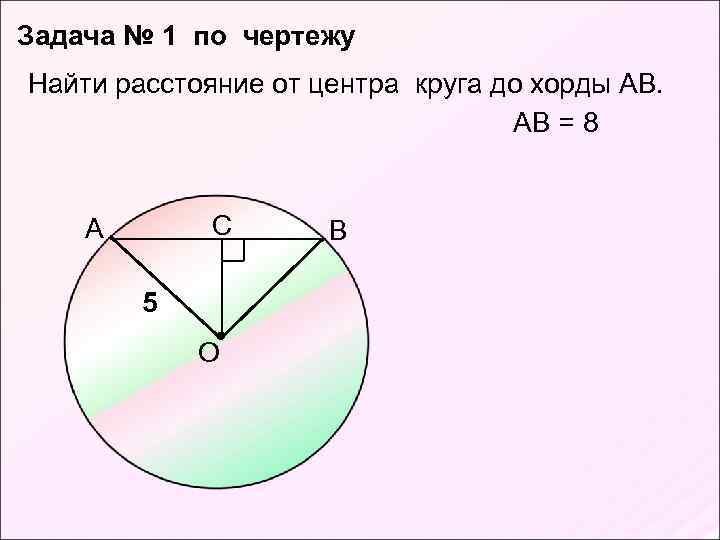Задача № 1 по чертежу Найти расстояние от центра круга до хорды АВ. АВ = 8 С А 5 О В