Циклические коды.pptx
- Количество слайдов: 12

ЦИКЛИЧЕСКИЕ КОДЫ -Циклические коды- это линейные коды, обладающие свойством цикличности. -Каждая циклическая перестановка кодового слова дает кодовое слово. 011 101 110 (сдвиг вправо) -Матричное представление циклических кодов очень громоздко. Существует полиномиальное представление циклических кодов. 000 0 011 х+1 101 х2+1

ЦИКЛИЧЕСКИЕ КОДЫ -Каждое кодовое слово может быть представлено в виде полинома. В каждое кодовое слово входит полином g(x), который является порождающим(эталонным). -Над полиномами определена операция умножения на полином по модулю xn+1, что равносильно сдвигу кодового слова влево. (X+1)*X = X 2+X (X 2+X)*X=X 2+1 011 110 101 -Понятие циклических кодов тесно связано с понятием полей Галуа

ПОЛЯ ГАЛУА -Поле Галуа- это поле, состоящие из конечного числа элементов. -Над элементами поля определены различные операции. Результат операции над элементами поля также является элементом поля. -Поле Галуа, где количество элементов поля есть простое число, является простым полем. 0 1 2 0 0 1 0 1 2 2 0 2 1 GF(3)

ПОЛЯ ГАЛУА

ПОЛЯ ГАЛУА -Полином a(x) делится на полином b(x), если существует такой полином q(x), что b(x)*q(x)=a(x). -Полиномы, которые делятся только на себя или на примитивный элемент поля называются неприводимыми. -НОД 2 -х полиномов есть нормированный полином наибольшей степени, на который делятся оба полинома. -НОК 2 -х полиномов есть нормированный полином наименьшей степени, который делится на оба полинома. -Кольцо полиномов над полем GF(q) по модулю P(x) является расширением поля GF(qm ) тогда и только тогда, когда P(x) является нормированным неприводимым полиномом степени m.

ПОЛЯ ГАЛУА -Пусть дано поле GF(4)=GF(22) в котором необходимо определить 0 1 Х Х+1 0 0 0 1 Х Х+1 Х 0 Х Х+1 1 Х+1 0 Х+1 1 Х операцию умножения. -Для этого необходимо определить неприводимый полином поля степени 2, т. е. данный полином не может быть разложен на элементы поля { 0, 1, X, X+1 }. -Этот полином имеет вид x 2+x+1, приравнивая полином к нулю получаем, что x 2=x+1. На основании этого строим поле.

ПОЛЯ ГАЛУА 1 X+1 X 1
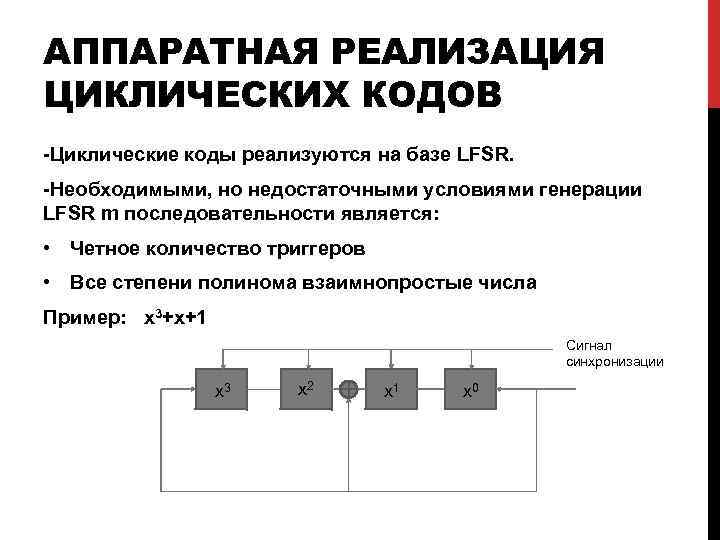
АППАРАТНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКИХ КОДОВ -Циклические коды реализуются на базе LFSR. -Необходимыми, но недостаточными условиями генерации LFSR m последовательности является: • Четное количество триггеров • Все степени полинома взаимнопростые числа Пример: x 3+x+1 Сигнал синхронизации x 3 x 2 x 1 x 0

ТЕОРЕМЫ И АЛГОРИТМЫ

АЛГОРИТМ ДЕКОДИРОВАНИЯ -Получатель получает сообщения + остаток, после этого он проводит такую же операцию над сообщением и сравнивает остатки. Если остатки одинаковые значит сообщение не содержит ошибок, иначе исправляем. -Обнаружение ошибок Пусть имеется порождающий полином g(x)m • L-1<m, обнаруживается любой пакет ошибок длины L • L-1=m, обнаруживается 1 -21 -m из всех L пакетов • L-1<m, обнаруживается 1 -2 m-1 из всех L пакетов

МАТРИЧНОЕ ПРЕДСТАВЛЕНИЯ g(x) g 0 … gn-k 0 … 0 g 0 x*g(x) g 1 … gn-k … 0 … … … … xk-1*g(x) 0 … 0 g 1 … gn-k

МАТРИЧНОЕ ПРЕДСТАВЛЕНИЯ -Проверочная матица имеет вид h(x) hk … h 0 0 … 0 hk x*h(x) H= = hk-1 … H 0 … … … … … xn-k-1*h(x) 0 … 0 hk hk-1 … h 0 -Умножая полученное сообщение на матрицу H(x) получаем синдром, характеризующий наличие ошибки
Циклические коды.pptx