Скачать презентацию Цифровые фильтры Часть 2 Нерекурсивные трансверсальные фильтры Скачать презентацию Цифровые фильтры Часть 2 Нерекурсивные трансверсальные фильтры

07 Цифровые фильтры-2.pptx

  • Количество слайдов: 43

Цифровые фильтры Часть 2 Цифровые фильтры Часть 2

Нерекурсивные (трансверсальные) фильтры • Трансверсальным ( Нерекурсивные (трансверсальные) фильтры • Трансверсальным ("поперечным") называется фильтр, осуществляющий взвешенное суммирование ряда отсчетов входного сигнала и не использующий выходные отсчеты: yi=a 0 xi+a 1 xi-1+. . . +amxi-m или

Нерекурсивные (трансверсальные) фильтры Системная функция нерекурсивного фильтра является конечной дробно-рациональной, с m-кратным полюсом при Нерекурсивные (трансверсальные) фильтры Системная функция нерекурсивного фильтра является конечной дробно-рациональной, с m-кратным полюсом при Z=0 и имеющей m нулей, определяемых коэффициентами {ak}.

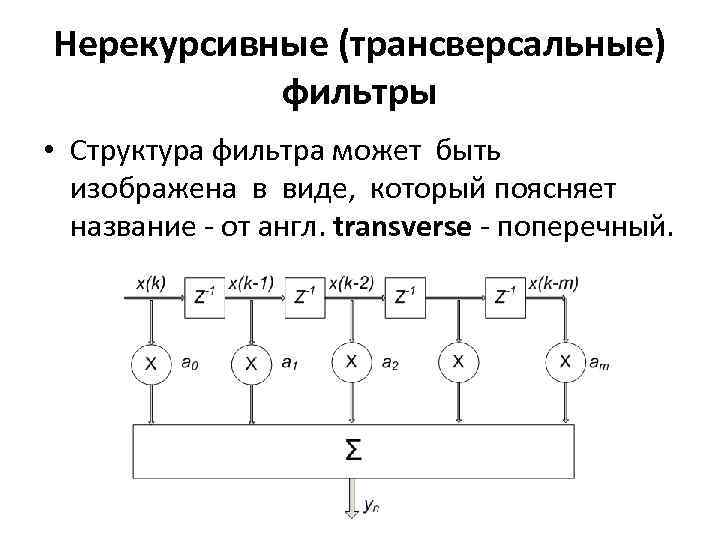Нерекурсивные (трансверсальные) фильтры • Структура фильтра может быть изображена в виде, который поясняет название Нерекурсивные (трансверсальные) фильтры • Структура фильтра может быть изображена в виде, который поясняет название - от англ. transverse - поперечный.

Нерекурсивные (трансверсальные) фильтры Если ввести замену ai =hi , то последнее выражение описывает алгоритм Нерекурсивные (трансверсальные) фильтры Если ввести замену ai =hi , то последнее выражение описывает алгоритм работы ЦФ в виде дискретной свертки входной последовательности с отсчетами импульсной характеристики. Таким образом, коэффициенты нерекурсивного фильтра являются отсчетами его импульсной характеристики {hm} = {a 0, a 1. . . ai. . . am}

Нерекурсивные (трансверсальные) фильтры Системная функция нерекурсивного фильтра является конечной дробно-рациональной, с m-кратным полюсом при Нерекурсивные (трансверсальные) фильтры Системная функция нерекурсивного фильтра является конечной дробно-рациональной, с m-кратным полюсом при Z=0 и имеющей m нулей, определяемых коэффициентами {ak}:

Нерекурсивные (трансверсальные) фильтры • Частотная характеристика трансверсального фильтра получается подстановкой Z=exp(j t) в H(z): Нерекурсивные (трансверсальные) фильтры • Частотная характеристика трансверсального фильтра получается подстановкой Z=exp(j t) в H(z): K(j ) = = a 0+a 1 exp(-j )+a 2 exp(-j 2 )+…+аmexp(-jm ) Подбором коэффициентов вид ЧХ можно видоизменять в широких пределах.

Пример ЦФ второго порядка, выполняющий усреднение трех отсчетов: yi=1/3(xi+xi-1+xi-2) Системная функция такого фильтра имеет Пример ЦФ второго порядка, выполняющий усреднение трех отсчетов: yi=1/3(xi+xi-1+xi-2) Системная функция такого фильтра имеет вид

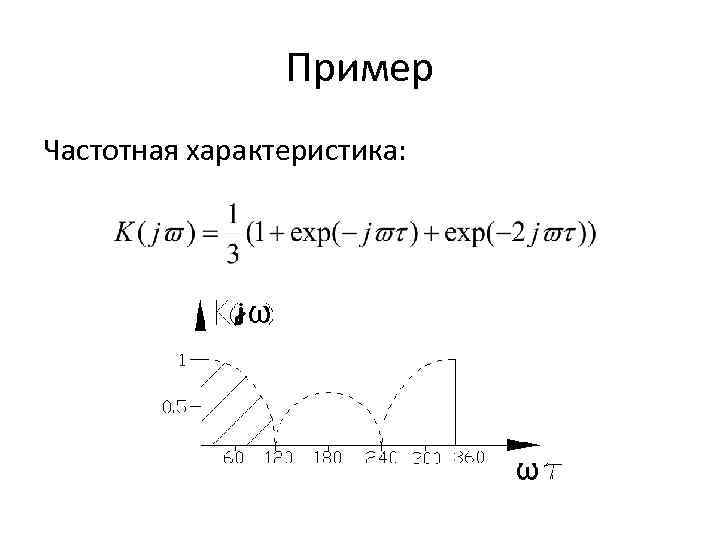Пример Частотная характеристика: Пример Частотная характеристика:

Достоинства КИХ-фильтров Достоинство нерекурсивных фильтров отсутствие в них условий для самовозбуждения. Поэтому данный тип Достоинства КИХ-фильтров Достоинство нерекурсивных фильтров отсутствие в них условий для самовозбуждения. Поэтому данный тип фильтра получил широкое распространение в технике.

Достоинства КИХ-фильтров Однако необходимо иметь ввиду, что если требуется фильтр с частотной характеристикой, близкой Достоинства КИХ-фильтров Однако необходимо иметь ввиду, что если требуется фильтр с частотной характеристикой, близкой к прямоугольной, то необходимое число звеньев (порядок фильтра) может достигать ста и более. В этом случае целесообразнее использовать рекурсивные фильтры.

Достоинства КИХ-фильтров Важным достоинством нерекурсивных фильтров является то, что в них легко может быть Достоинства КИХ-фильтров Важным достоинством нерекурсивных фильтров является то, что в них легко может быть обеспечена линейная ФЧХ, а значит, постоянная (не зависящая от частоты) фазовая и групповая задержка. Для этого необходимо, чтобы импульсная характеристика фильтра была симметричной: ak =am-k или антисимметричной: ak = -am-k

Фазо-частотная характеристика КИХ-фильтров • Фазовая задержка – это фаза первого выходного отсчета фильтра относительно Фазо-частотная характеристика КИХ-фильтров • Фазовая задержка – это фаза первого выходного отсчета фильтра относительно первого входного отсчета. • ФЧХ КИХ-фильтров линейна в полосе пропускания. • Для фильтров с симметричными коэффициентами фазовый сдвиг в полосе пропускания является линейной функцией частоты.

Групповая задержка • Групповая задержка – это производная ФЧХ по частоте, взятая с обратным Групповая задержка • Групповая задержка – это производная ФЧХ по частоте, взятая с обратным знаком. • Когда групповая задержка постоянна (то есть, ФЧХ линейна), все частотные компоненты входного сигнала задерживаются на его выходе одинаково. • Это значит, что сигнал не подвергается фазовым искажениям; а это критически важно для коммутационных сигналов.

Необходимость постоянства групповой задержки • Если для передачи данных используется многочастотная модуляция, то все Необходимость постоянства групповой задержки • Если для передачи данных используется многочастотная модуляция, то все частотные компоненты должны проходить через фильтр с одинаковой задержкой. • В противном случае возникнет рассинхронизация каналов данных.

АНАЛИЗ КИХ-ФИЛЬТРОВ АНАЛИЗ КИХ-ФИЛЬТРОВ

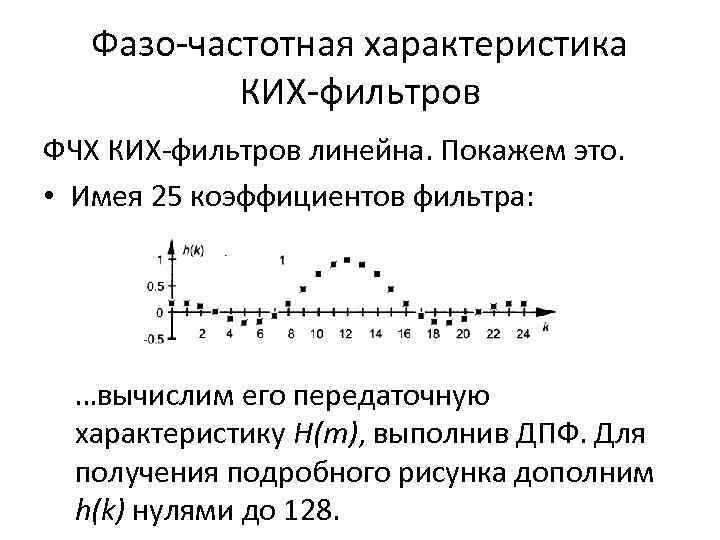Фазо-частотная характеристика КИХ-фильтров ФЧХ КИХ-фильтров линейна. Покажем это. • Имея 25 коэффициентов фильтра: …вычислим Фазо-частотная характеристика КИХ-фильтров ФЧХ КИХ-фильтров линейна. Покажем это. • Имея 25 коэффициентов фильтра: …вычислим его передаточную характеристику H(m), выполнив ДПФ. Для получения подробного рисунка дополним h(k) нулями до 128.

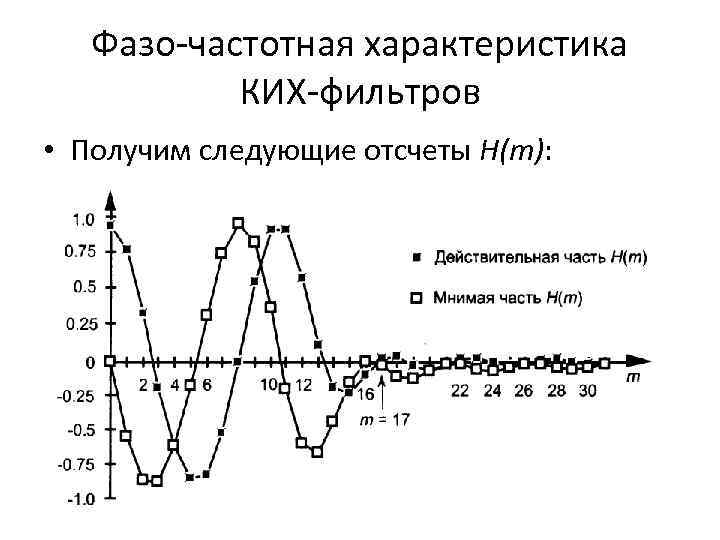Фазо-частотная характеристика КИХ-фильтров • Получим следующие отсчеты H(m): 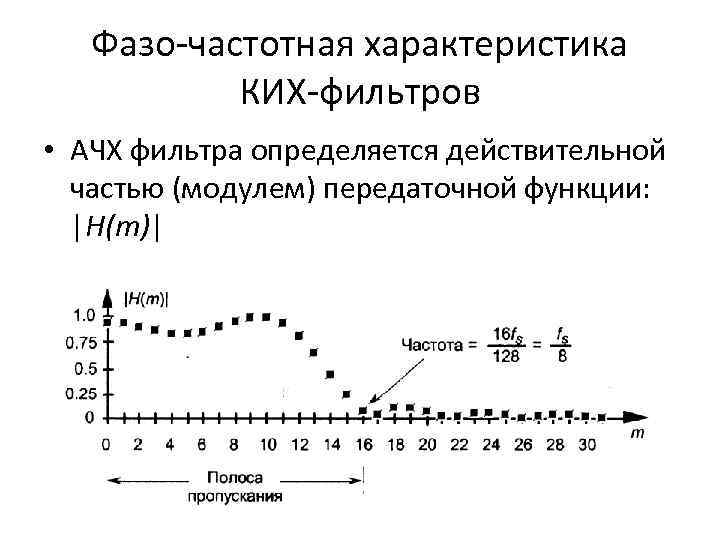Фазо-частотная характеристика КИХ-фильтров • Получим следующие отсчеты H(m):

Фазо-частотная характеристика КИХ-фильтров • АЧХ фильтра определяется действительной частью (модулем) передаточной функции: |H(m)| Фазо-частотная характеристика КИХ-фильтров • АЧХ фильтра определяется действительной частью (модулем) передаточной функции: |H(m)|

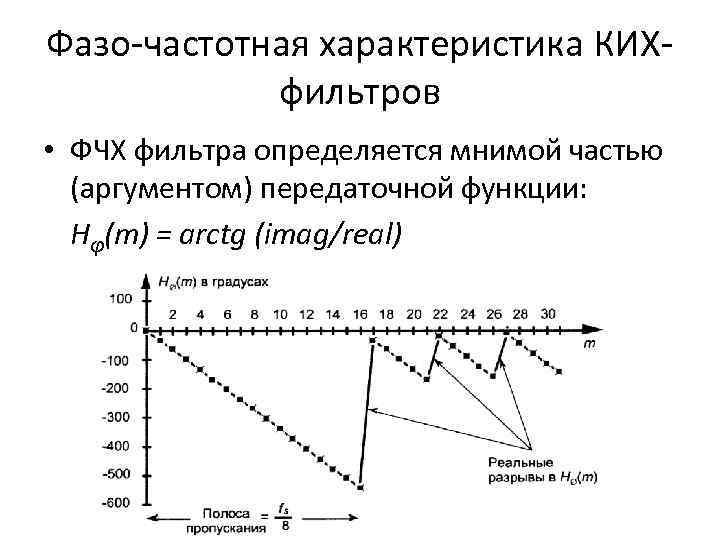Фазо-частотная характеристика КИХфильтров • ФЧХ фильтра определяется мнимой частью (аргументом) передаточной функции: Hφ(m) = Фазо-частотная характеристика КИХфильтров • ФЧХ фильтра определяется мнимой частью (аргументом) передаточной функции: Hφ(m) = arctg (imag/real)

Фазо-частотная характеристика КИХ-фильтров • ФЧХ линейна в полосе пропускания. • На отсчете 17 H(m) Фазо-частотная характеристика КИХ-фильтров • ФЧХ линейна в полосе пропускания. • На отсчете 17 H(m) претерпевает изменение знака действительной части, а мнимая часть остается отрицательной: это приводит к разрыву ФЧХ. • Каждое изменение знака действительной части приводит к появлению разрыва ФЧХ.

РЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ РЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ

РЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ В таких фильтрах выходной сигнал РЦФ в каждый момент времени формируется РЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ В таких фильтрах выходной сигнал РЦФ в каждый момент времени формируется не только из входных, но и ряда предшествующих отсчетов. Системная функция РЦФ имеет вид:

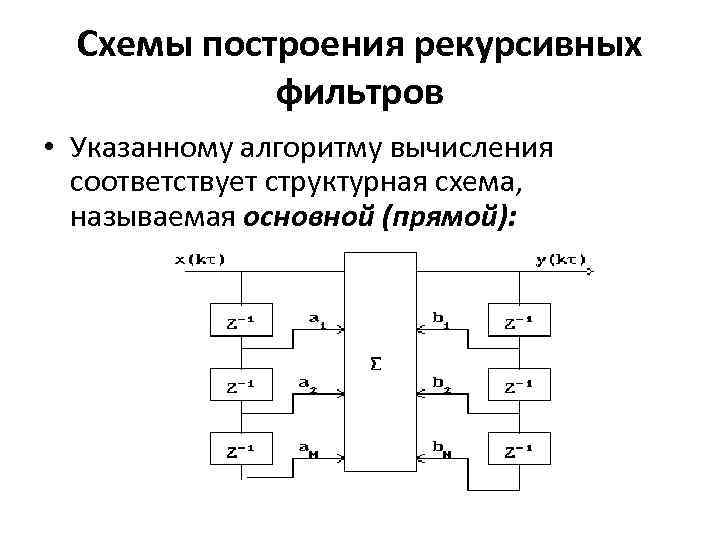Схемы построения рекурсивных фильтров • Указанному алгоритму вычисления соответствует структурная схема, называемая основной (прямой): Схемы построения рекурсивных фильтров • Указанному алгоритму вычисления соответствует структурная схема, называемая основной (прямой):

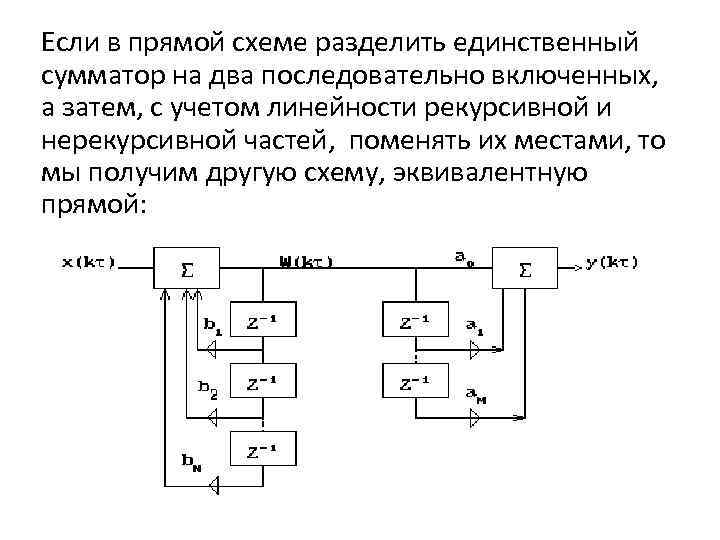Если в прямой схеме разделить единственный сумматор на два последовательно включенных, а затем, с Если в прямой схеме разделить единственный сумматор на два последовательно включенных, а затем, с учетом линейности рекурсивной и нерекурсивной частей, поменять их местами, то мы получим другую схему, эквивалентную прямой:

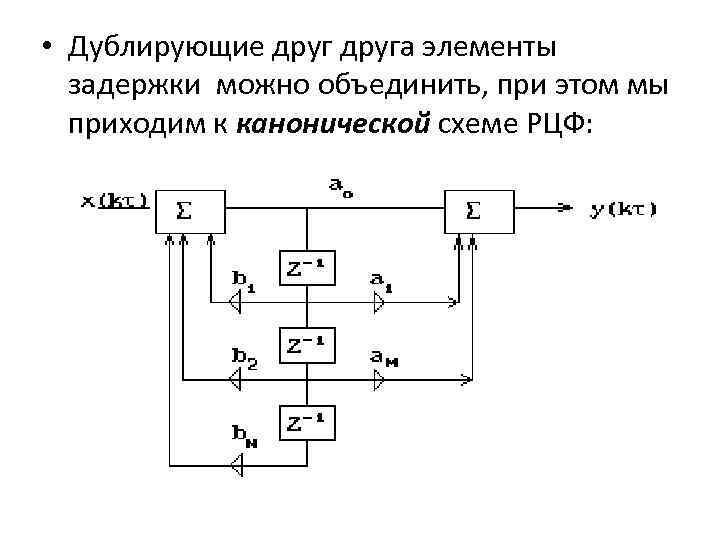• Дублирующие друга элементы задержки можно объединить, при этом мы приходим к канонической • Дублирующие друга элементы задержки можно объединить, при этом мы приходим к канонической схеме РЦФ:

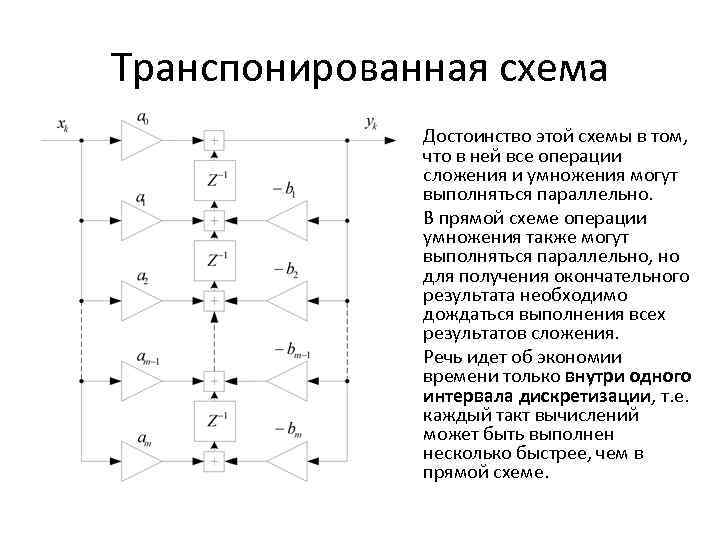Транспонированная схема Достоинство этой схемы в том, что в ней все операции сложения и Транспонированная схема Достоинство этой схемы в том, что в ней все операции сложения и умножения могут выполняться параллельно. В прямой схеме операции умножения также могут выполняться параллельно, но для получения окончательного результата необходимо дождаться выполнения всех результатов сложения. Речь идет об экономии времени только внутри одного интервала дискретизации, т. е. каждый такт вычислений может быть выполнен несколько быстрее, чем в прямой схеме.

Устойчивость ЦФ • Нерекурсивные фильтры не имеют цепей обратной связи и поэтому всегда устойчивы. Устойчивость ЦФ • Нерекурсивные фильтры не имеют цепей обратной связи и поэтому всегда устойчивы. • В рекурсивном фильтре, из-за наличия обратной связи, при некоторой заданной последовательности начальных состояний на выходе могут циклически образовываться отсчеты, играющие роль «свободных колебаний» .

Устойчивость ЦФ: определение • ЦФ называется устойчивым, если независимо от начальных условий свободный процесс Устойчивость ЦФ: определение • ЦФ называется устойчивым, если независимо от начальных условий свободный процесс в нем представляет невозрастающую последовательность, т. е. при n yn

Критерий устойчивости • Если передаточная (системная) функция ЦФ представляет собой несократимую дробь, то для Критерий устойчивости • Если передаточная (системная) функция ЦФ представляет собой несократимую дробь, то для устойчивости фильтра необходимо и достаточно, чтобы выполнялось условие Zi 1, i=1, 2, . . . , N, где Zi - полюсы (корни знаменателя) H(Z). То есть, полюсы должны лежать внутри единичной окружности.

Критерий устойчивости • Это условие базируется на теории устойчивости аналоговых цепей. Известно, что аналоговая Критерий устойчивости • Это условие базируется на теории устойчивости аналоговых цепей. Известно, что аналоговая схема устойчива, если полюсы ее передаточной функции расположены в левой половине плоскости P.

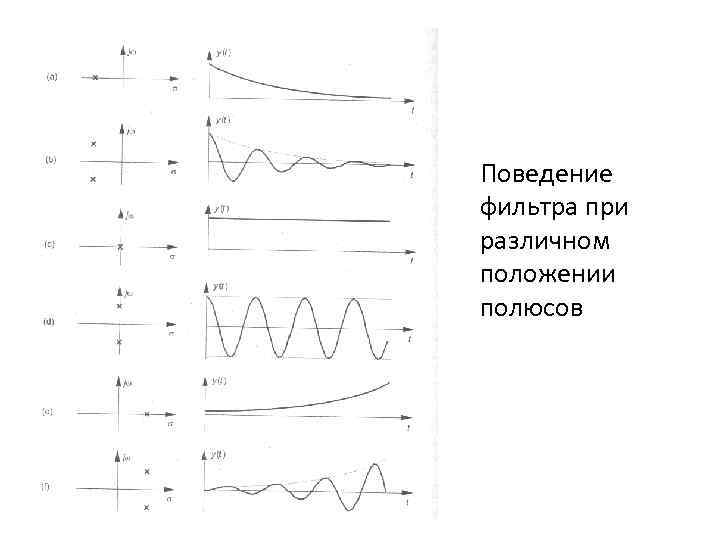Поведение фильтра при различном положении полюсов Поведение фильтра при различном положении полюсов

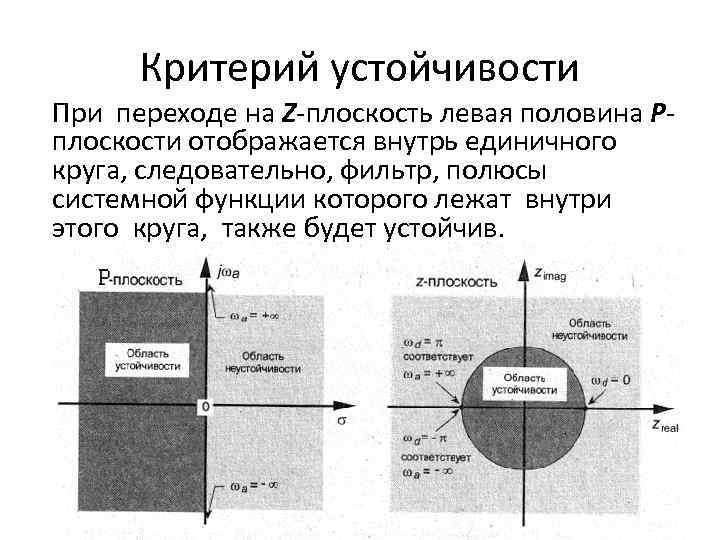Критерий устойчивости При переходе на Z-плоскость левая половина Pплоскости отображается внутрь единичного круга, следовательно, Критерий устойчивости При переходе на Z-плоскость левая половина Pплоскости отображается внутрь единичного круга, следовательно, фильтр, полюсы системной функции которого лежат внутри этого круга, также будет устойчив.

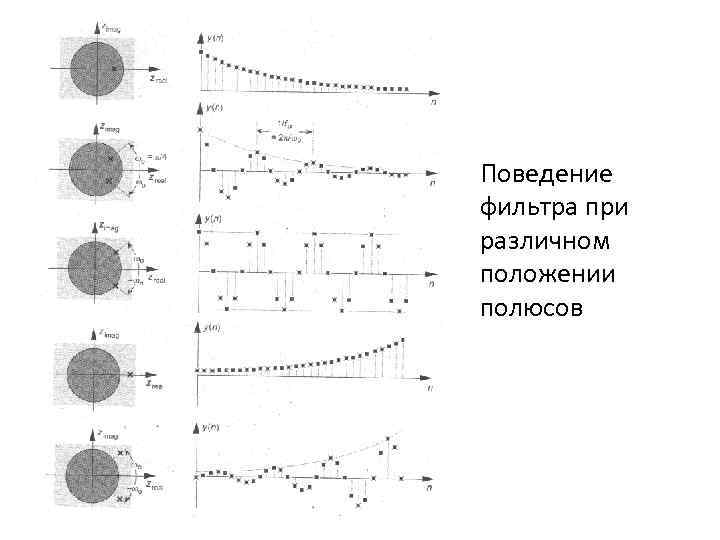Поведение фильтра при различном положении полюсов Поведение фильтра при различном положении полюсов

Применение неустойчивых фильтров Неустойчивый фильтр неработоспособен, когда входной сигнал действует неограниченно долго, поскольку при Применение неустойчивых фильтров Неустойчивый фильтр неработоспособен, когда входной сигнал действует неограниченно долго, поскольку при этом выходной сигнал рано или поздно перестает зависеть от входного. В тех случаях, когда входной сигнал существует в течение ограниченного времени, фильтр может быть устойчив и применяться на практике.

Применение неустойчивых фильтров Например, цифровой интегратор с передаточной функцией (полюс в точке Z=1) вполне Применение неустойчивых фильтров Например, цифровой интегратор с передаточной функцией (полюс в точке Z=1) вполне работоспособен, если входной сигнал существует на конечном интервале, а после происходит сброс фильтра. То есть, восстанавливаются нулевые начальные условия.

Примеры полюс Z 1=0. 3 ; Z 1 < 1: фильтр устойчив. полюс Z Примеры полюс Z 1=0. 3 ; Z 1 < 1: фильтр устойчив. полюс Z 1=2; Z 1 > 1 фильтр неустойчив. Устойчив.

Использование Z-преобразования для анализа БИХ-фильтра • Рассмотрим БИХ-фильтр второго порядка, частота среза коего равна Использование Z-преобразования для анализа БИХ-фильтра • Рассмотрим БИХ-фильтр второго порядка, частота среза коего равна f. Д/10: y(n) = = 0. 0605 x(n) + 0. 121 x(n-1) + 0. 0605 x(n-2) + +1. 194 y(n-1) – 0. 436 y(n-2)

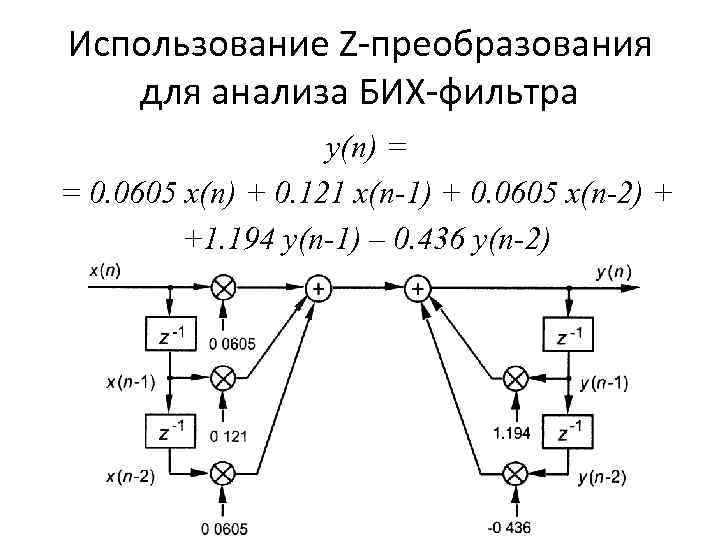Использование Z-преобразования для анализа БИХ-фильтра y(n) = = 0. 0605 x(n) + 0. 121 Использование Z-преобразования для анализа БИХ-фильтра y(n) = = 0. 0605 x(n) + 0. 121 x(n-1) + 0. 0605 x(n-2) + +1. 194 y(n-1) – 0. 436 y(n-2)

Использование Z-преобразования для анализа БИХ-фильтра • В Z-области уравнение фильтра имеет вид: Y(z) = Использование Z-преобразования для анализа БИХ-фильтра • В Z-области уравнение фильтра имеет вид: Y(z) = 0. 0605 X(z) + 0. 121 X(z) z-1 + 0. 0605 X(z) z-2 + + 1. 194 Y(z) z-1 – 0. 436 Y(z) z-2 • Запишем передаточную функцию фильтра:

Использование Z-преобразования для анализа БИХ-фильтра • Подставив z=ejω, получим частотную характеристику: • С учетом Использование Z-преобразования для анализа БИХ-фильтра • Подставив z=ejω, получим частотную характеристику: • С учетом тождеств Эйлера:

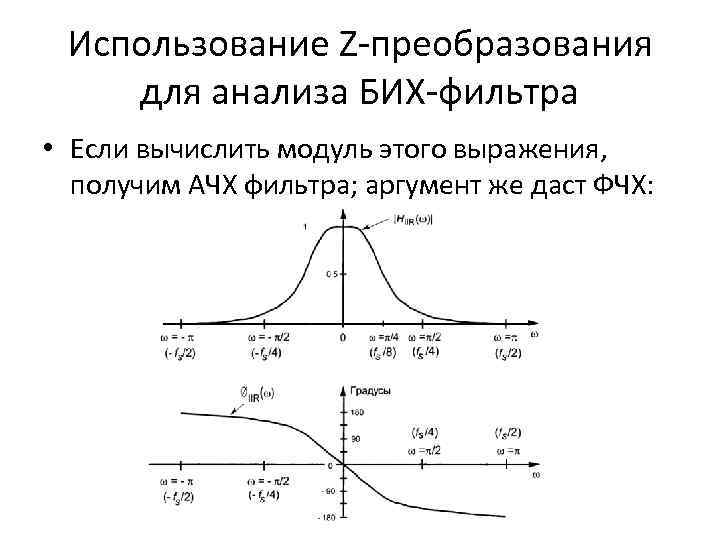Использование Z-преобразования для анализа БИХ-фильтра • Если вычислить модуль этого выражения, получим АЧХ фильтра; Использование Z-преобразования для анализа БИХ-фильтра • Если вычислить модуль этого выражения, получим АЧХ фильтра; аргумент же даст ФЧХ:

Использование Z-преобразования для анализа БИХ-фильтра • ФЧХ БИХ-фильтра нелинейна. Это неотъемлемое свойство БИХ-фильтров. • Использование Z-преобразования для анализа БИХ-фильтра • ФЧХ БИХ-фильтра нелинейна. Это неотъемлемое свойство БИХ-фильтров. • То есть, компоненты входного сигнала различных частот придут на выход с различной задержкой. • Это может вызвать искажение информации при передаче данных с кодированием многофазной модуляцией.