Цифровые фильтры Часть 1 Линейность и стационарность

Цифровые фильтры Часть 1

Линейность и стационарность Мы будем рассматривать линейные стационарные цепи. Линейными называются системы, для которых справедлив принцип суперпозиции: сумма эффектов от отдельных воздействий равна эффекту от суммы воздействий. С точки зрения спектральных свойств линейность означает отсутствие на выходе ЦФ гармоник, не присутствовавших во входном сигнале. Стационарность означает постоянство характеристик системы во времени: в стационарной системе произвольная задержка входного сигнала приводит только к такой же задержке выходного сигнала и не меняет его формы. Если это условие не выполняется, система называется нестационарной, параметрической, или системой с переменными параметрами.

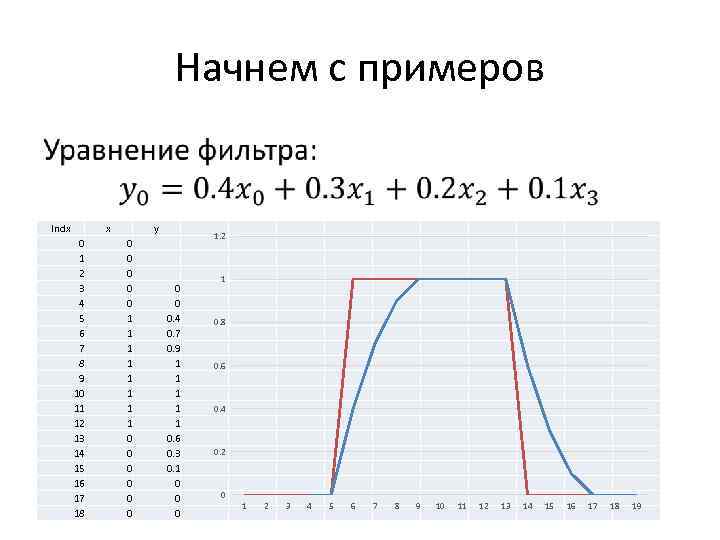Начнем с примеров • Indx x 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 y 0 0 0 1 1 1 1 0 0 0 1. 2 0 0 0. 4 0. 7 0. 9 1 1 1 0. 6 0. 3 0. 1 0 0 0 1 0. 8 0. 6 0. 4 0. 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

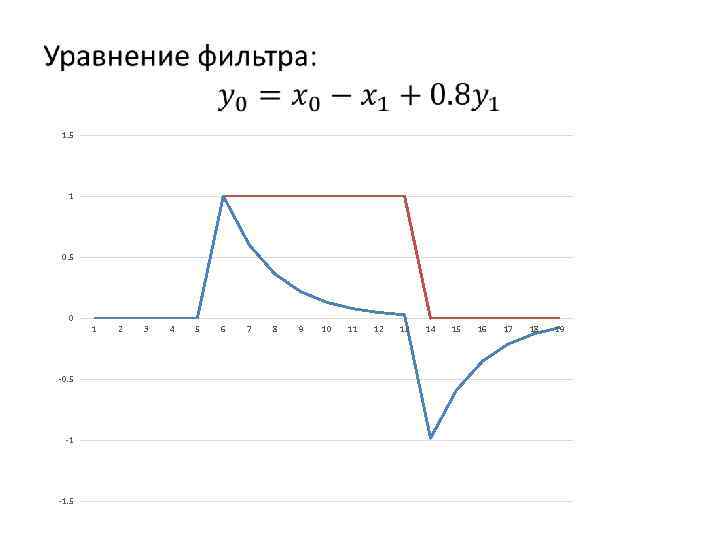• 1. 5 1 0. 5 0 -0. 5 -1 -1. 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Описание ЦФ с помощью разностных уравнений В теории аналоговых цепей связь между выходным и входным сигналами может быть описана с помощью дифференциального уравнения где x(t) - входной сигнал; y(t) - выходной сигнал; ai , bi - постоянные коэффициенты, на которые умножаются соответственно входные и выходные отсчеты.

Описание ЦФ с помощью разностных уравнений • В ЦФ вместо дифференциальных должны использоваться разностные уравнения, где вместо производных dy/dt фигурирует разность соседних значений сигнала, отнесенная к интервалу дискретизации:

• Результат таков:

Обратная связь Кроме входных отсчетов, фильтр может использовать и выходные отсчеты, рассчитанные в предыдущие моменты времени. В этом случае для дискретного фильтра первого порядка разностное уравнение имеет вид y(k )-by(k - )=ax(k ) или y(k )=ax(k )+by(k - )

Для того, чтобы частотная характеристика фильтра была нетривиальной, то есть различалась на разных частотах, выходной сигнал должен зависеть от нескольких отсчетов, полученных в разные моменты времени. То есть, фильтр должен обладать памятью.

Импульсная характеристика ЦФ В аналоговой технике импульсная характеристика – это реакция системы на сигнал в виде дельта-функции. Сигнал на выходе системы может быть представлен в виде свертки входного сигнала с импульсной характеристикой:

Импульсная характеристика ЦФ • В ЦОС импульсная характеристика цифрового фильтра определяется как его отклик на сигнал в виде единичного импульса. Единичный импульс является дискретным аналогом дельта-функции:

Импульсная характеристика ЦФ • Импульсная характеристика цифрового фильтра, представляющая собой последовательность отсчетов, для физически реализуемого ЦФ должна удовлетворять условию hk=h(k ) при k>0. • Стационарность применительно к ЦФ означает, что при смещении входного единичного импульса на любое число интервалов дискретизации на столько же интервалов без изменения формы смещается отклик h(k )

• Сигнал на выходе ЦФ определяется как дискретная свертка входного сигнала и импульсной характеристики фильтра:

Передаточная характеристика и системная функция • Для аналоговых цепей, описываемых в операторной форме с помощью преобразования Лапласа, вводится понятие передаточной функции, которая определяется как отношение преобразований Лапласа выходного и входного сигналов:

Передаточная характеристика и системная функция • Поскольку выходной сигнал фильтра y(k ) определяется свёрткой импульсной характеристики фильтра h(k ) и входной последовательности, то, применяя к нему теорему о Z-преобразовании свертки, получаем

Передаточная характеристика и системная функция • Аналогом передаточной функции для дискретных систем является системная функция H(z). По определению, системной функцией цифрового фильтра называется Z-преобразование его импульсной характеристики:

Системная функция ЦФ, заданного разностным уравнением Применим Z- преобразование к обеим частям уравнения: Системная функция физически реализуемого цифрового фильтра является дробно-рациональной.

Частотная характеристика Частотный коэффициент передачи Для аналогового фильтра частотная характеристика определяется как отношение спектра сигнала на выходе S 2(j ) к спектру сигнала на входе S 1(j ) :

Частотная характеристика Частотный коэффициент передачи Введем понятие гармонической последовательности x(k )=exp(+j k ); -

Частотная характеристика Частотный коэффициент передачи Сигнал на выходе ЦФ представляет последовательность той же частоты, что и входной сигнал, отсчеты которой получаются путем умножения входных отсчетов на комплексное число K(j ) - зависящее от , и {hn}.

Частотная характеристика Частотный коэффициент передачи Частотная характеристика ЦФ связана с его системной функцией соотношением K(j )=H(exp(j )) , то есть получается заменой Z-1 на exp(-j ). Таким образом, ЧХЦФ равна системной функции, вычисленной на окружности единичного радиуса.

Свойства ЧКП ЦФ • K(j ) - периодическая функция частоты с периодом d: K(j )=K[j( +n d)] • K(j ) есть преобразование Фурье от {hn}, представленной в форме h(t) = h 0 (t) + h 1 (t- )+. . . , т. е. K(j ) есть ДПФ от импульсной характеристики.

Обобщим: Физически реализуемый ЦФ, работающий в реальном масштабе времени, может использовать для формирования k-го отсчета выходного сигнала: • текущее и М предшествующих значений входного сигнала: xk; xk-1; . . . ; xk-M; • N предшествующих значений выходного сигнала yk-1; yk-2; . . . ; yk-N.

Обобщим: Эти отсчеты должны обрабатываться в соответствии с алгоритмом Числа M и N определяют порядок рекурсивной и нерекурсивной частей фильтра.

Рекурсивные и нерекурсивные ЦФ • В зависимости от того, используются или нет при формировании текущего выходного отсчета предшествующие выходные значения, цифровые фильтры делятся на два класса - рекурсивные и нерекурсивные.

Рекурсивные и нерекурсивные ЦФ Если все коэффициенты bj=0, то есть, предшествующие выходные отсчеты не используются, то фильтр носит название нерекурсивного. Импульсная характеристика такого фильтра и длительность переходного процесса полностью определяется конечным числом M коэффициентов ai , следовательно, h(i)=0 при i>=M. Поэтому нерекурсивные фильтры называют фильтрами с конечной импульсной характеристикой (КИХ).

Рекурсивные и нерекурсивные ЦФ Если хотя бы один из коэффициентов bj 0, т. е. в фильтре имеется обратная связь с выхода на вход, то фильтр называется рекурсивным. Из-за наличия обратной связи отклик фильтра на единичный импульс может длиться бесконечно долго, т. е. импульсная характеристика рекурсивных фильтров, в принципе, может иметь бесконечную протяженность, поэтому их часто именуют фильтрами с бесконечной импульсной характеристикой (БИХ).

Рекурсивные и нерекурсивные ЦФ На практике обычно используются фильтры БИХ с быстро спадающей импульсной характеристикой, т. к. протяженный отклик на единичное воздействие означает, что фильтр находится в неустойчивом состоянии или близок к нему. Числа M и N определяют порядок рекурсивной и нерекурсивной части фильтра.