Цифровая сортировка Digital Sort Пусть дана последовательность из

Цифровая сортировка Digital Sort Пусть дана последовательность из S чисел, в m – ичной системе счисления. Каждое число состоит из L цифр d 1 d 2…d. L, 0 ≤ di ≤ m – 1, i=1. . L. Q 0 , Q 1…Qm-1 – m очередей. Для понимания сути сортировки рассмотрим пример:

S : 31 Q 0 : 20 Q 1 : 31 Q 2 : 02 Q 3 : 03’ S : 20 Q 0 : 02 Q 1 : Q 2 : 20 Q 3 : 30 S : 02 03’ 20 02 03” 33 30 21 03” 33 30 31 21 02 03’ 03” 33 03’ 03” 21 31 33 03’ 03” 20 21 30 31 33

Вначале числа из списка S распределяются по m очередям, причём номер очереди определяется последней цифрой каждого числа. Затем полученные очереди соединяются в список, для которого все действия повторяются, но распределение по очередям производится в соответствии со следующей цифрой и т. д. Количество разбиений равно количеству цифр в числе. В данном примере использованы 4 очереди, т. к. каждая цифра принимает значение от 0 до 3, т. е. четверичная система счисления. В десятичной системе – 10 очередей. Пример: целые числа long int 4 б, 32 бита байт=цифре, т. е. 256 очередей в диапазоне от 0 до 255.

Схема алгоритма DO (j=L, L– 1, … , 1) <инициализация очередей Q> <расстановка элементов из списка S в очереди Q по j – ой цифре > <соединение очередей Q в список S > OD Определение j-ой цифры сортировки tdata – тип элементов данных tdata

Для решения задачи выделения байта лучше подходит кодировка UNION. long int byte [4] Необходимый в структуре элемент списка определяет массив байтов, который накладывается на компоненту data. srtuct t. LE { t. LE * next; UNION { t. Data; byte Digit [sizeof (t. Data)]; } } Тогда доступ к каждому k-тому байту: Digit[k] Рассмотрим особенности реализации сортировки для сложных полей(структур) srtuct t. Data { char name [5]; long phone; }

sizeof (t. Data) - 10 байтов. name phone Используем индексацию для удобства выбора байта. Введем индексный массив: KDI(key Digit Index) = sizeof (t. Data) KDI [j] - номер байта Пример: 1) ключ = name, KDI = (1, 2, 3, 4, 5) 2) ключ = phone, KDI = (10, 9, 8, 7) 3) ключ = phone + name, KDI = (10, 9, 8, 7 , 1, 2, 3, 4, 5) 4) ключ = 3 младших байта phone + 3 первых буквы name KDI = (9, 8, 7 , 1, 2, 3) k=KDI[j] d=Digit[k] ∿d = Digit[d. KDI[j]] }

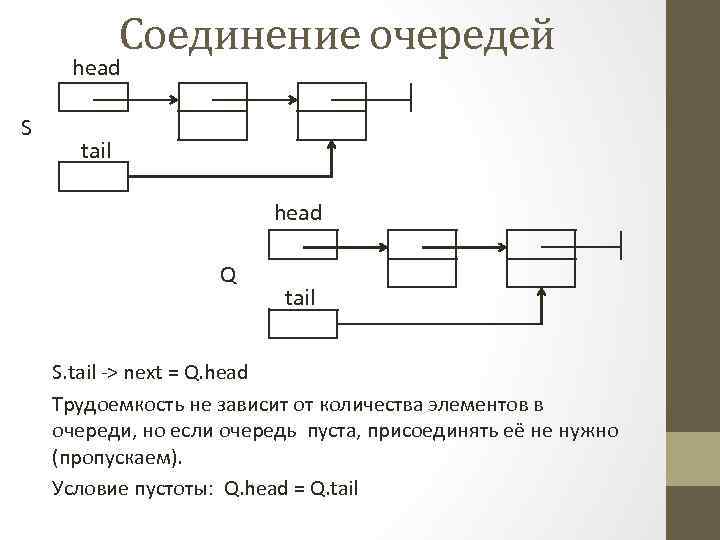Соединение очередей head S tail head Q tail S. tail -> next = Q. head Трудоемкость не зависит от количества элементов в очереди, но если очередь пуста, присоединять её не нужно (пропускаем). Условие пустоты: Q. head = Q. tail

Цифровая сортировка DO (j=L, L-1, … 1) DO (i=0, 1, … 255) Q i. Tail: = & Q i. Head OD p: =S DO (p ≠ NIL) d: =p → Digit[j] Q d. Tail → Next: =p Q d. Tail: =p p: =p → Next OD p: =& S DO (i=0, 1, … 255) IF (Q i. Tail ≠ & Q i. Head) p → Next: =Qi. Head p: =Q i. Tail FI OD p → Next: =NIL OD

T = O( L ( n + m ) = O ( n ) Чтобы изменить направление сортировки на обратный, нужно очереди соединить в обратном порядке. Недостатки: 1) Метод применим, если задача сортировки сводится к задаче упорядоченности чисел. 2) Если длина L велика, то метод может проигрывать методу Хоара (Quick Sort). ( При L = 8 Digital Sort хуже Quick Sort)