Чурюмов Александр Юрьевич Организация эксперимента Лекция 3

Чурюмов Александр Юрьевич Организация эксперимента Лекция 3

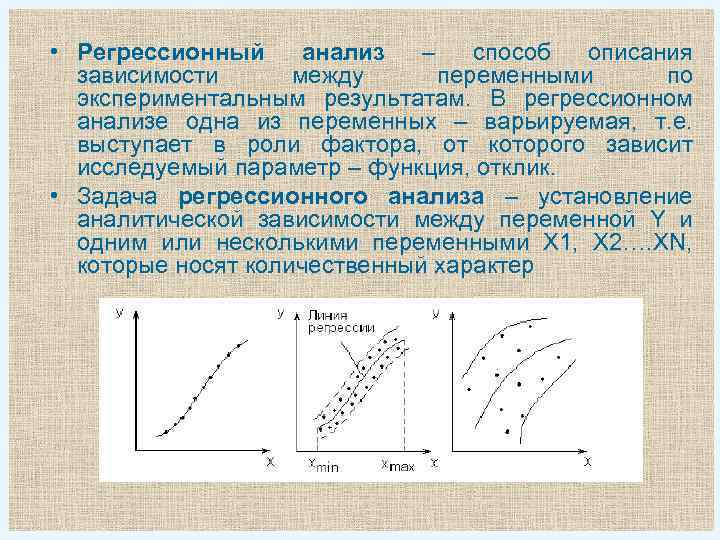• Регрессионный анализ – способ описания зависимости между переменными по экспериментальным результатам. В регрессионном анализе одна из переменных – варьируемая, т. е. выступает в роли фактора, от которого зависит исследуемый параметр – функция, отклик. • Задача регрессионного анализа – установление аналитической зависимости между переменной Y и одним или несколькими переменными X 1, X 2…. XN, которые носят количественный характер

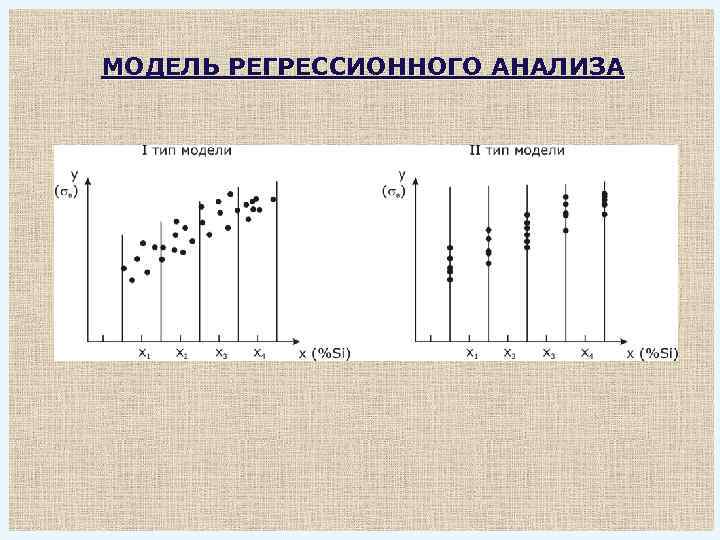МОДЕЛЬ РЕГРЕССИОННОГО АНАЛИЗА

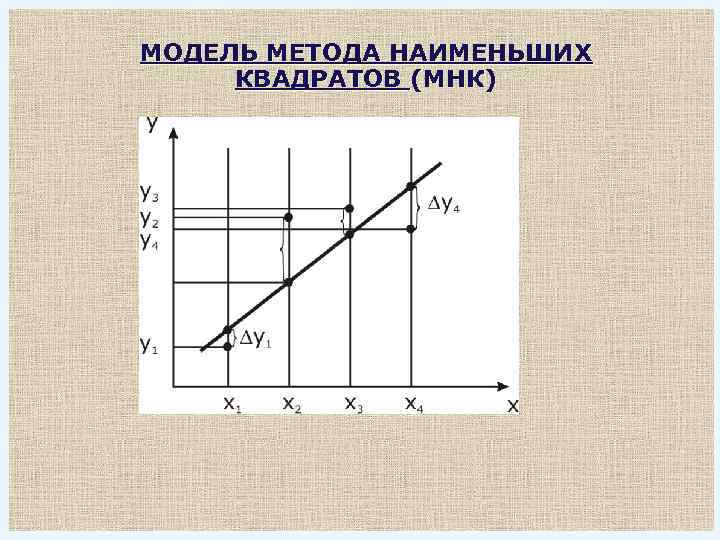МОДЕЛЬ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ (МНК)

Определение коэффициентов уравнения регрессии n - число экспериментальных точек Необходимое условие минимума

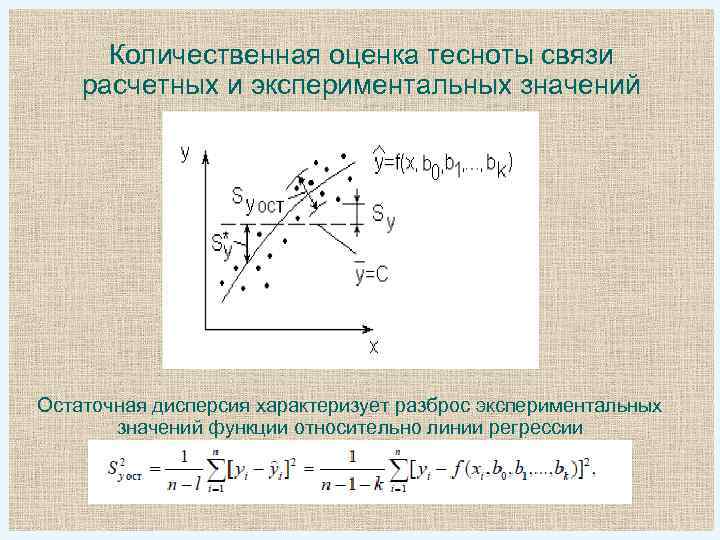Количественная оценка тесноты связи расчетных и экспериментальных значений Остаточная дисперсия характеризует разброс экспериментальных значений функции относительно линии регрессии

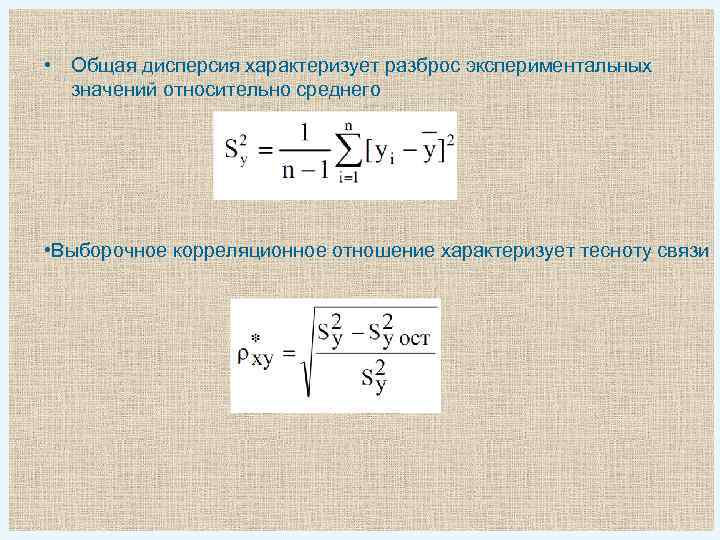• Общая дисперсия характеризует разброс экспериментальных значений относительно среднего • Выборочное корреляционное отношение характеризует тесноту связи

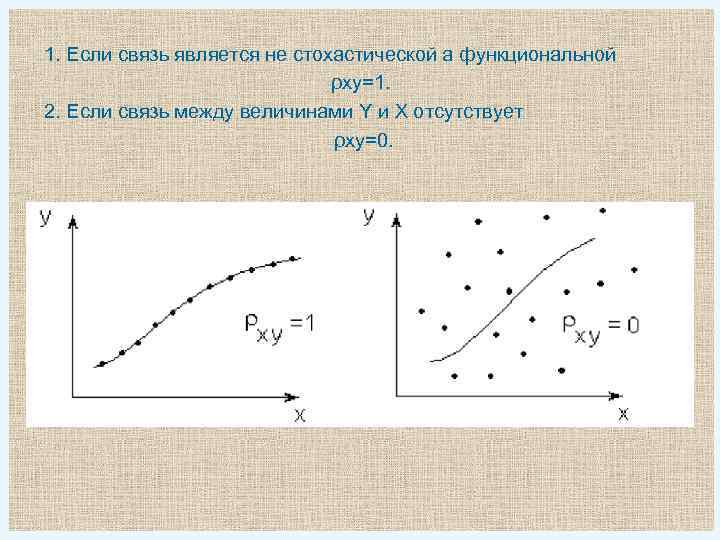1. Если связь является не стохастической а функциональной ρxy=1. 2. Если связь между величинами Y и X отсутствует ρxy=0.

Линейная регрессия

Проверка адекватности модели 1. Определяется среднее из параллельных опытов при x=xi (m* число опытов при x=xi) 2. Рассчитываются значения параметра y по уравнению регрессии при x = xi. 3. Рассчитывается дисперсия адекватности 4. Определяется выборочная дисперсия

5. Определяется дисперсия воспроизводимости 6. Определяется расчетной значение критерия Фишера 7. Определяется расчетное значение критерия Фишера F (α, m 1, m 2), где m 1=n-l, m 2= n(m*-1). 8. Если F

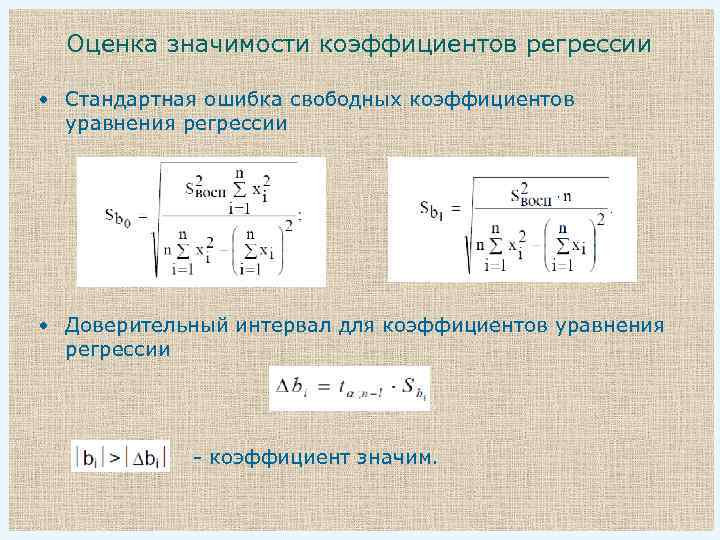Оценка значимости коэффициентов регрессии • Стандартная ошибка свободных коэффициентов уравнения регрессии • Доверительный интервал для коэффициентов уравнения регрессии - коэффициент значим.

МАТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА • Цели планирования многофакторных экспериментов: • построение многофакторной регрессионной • модели; • нахождение значений факторов, при которых • отклик оптимален;

РЕАЛЬНЫЕ И КОДИРОВАННЫЕ ЗНАЧЕНИЯ ФАКТОРОВ - реальные значения факторов; - кодированные значения факторов; - максимальное (верхнее) значение; - минимальное (нижнее) значение; - среднее (основное) значение; - интервал варьирования;

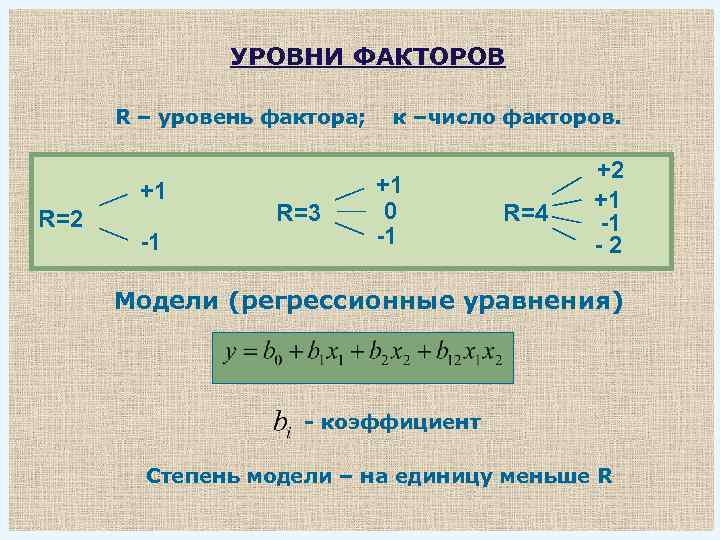УРОВНИ ФАКТОРОВ R – уровень фактора; +1 R=2 -1 R=3 к –число факторов. +1 0 -1 R=4 +2 +1 -1 -2 Модели (регрессионные уравнения) - коэффициент Степень модели – на единицу меньше R

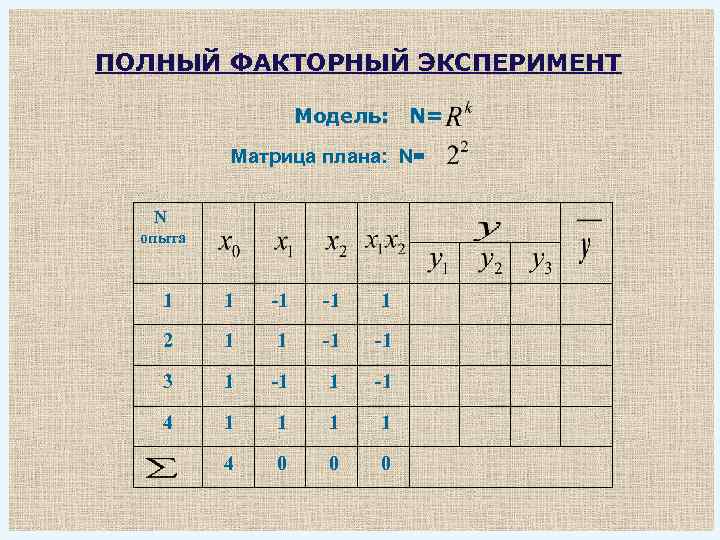ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ Модель: N= Матрица плана: N= N опыта 1 1 -1 -1 1 2 1 1 -1 -1 3 1 -1 4 1 1 4 0 0 0

СВОЙСТВА ПЛАНА ПФЭ 1. Симметричность 2. Ортогональность 3. Нормированность Регрессионная модель плана главные эффекты взаимодействия

ПЛАН В НАТУРАЛЬНЫХ ЗНАЧЕНИЯХ ФАКТОРОВ -содержание углерода в чугуне - содержание кремния в чугуне ПФЭ - глубина отбела (Н) N опыта 1 3, 5 1, 2 2 3, 9 1, 2 3 3, 5 2, 2 4 3, 9 2, 2

РАСЧЕТ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ( Это – расчетные значения) - экспериментальные значения (по плану) (принцип МНК)

ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ N= ; ; N опыта 1 - - + 2 + - - 3 - + - 4 + + + N= - число введенных факторов , N= Модель:

КОЭФФИЦИЕНТЫ УРАВНЕНИЯ - генерирующее соотношение - определяющий контраст - смешивание коэффициентов (совместная оценка)

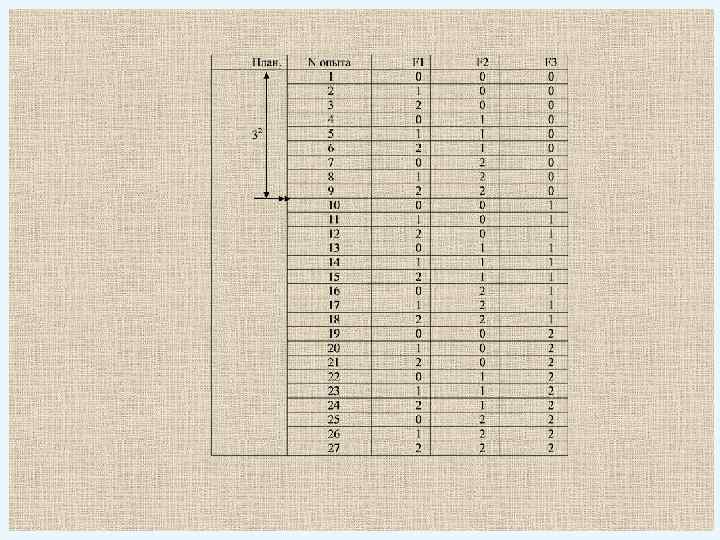
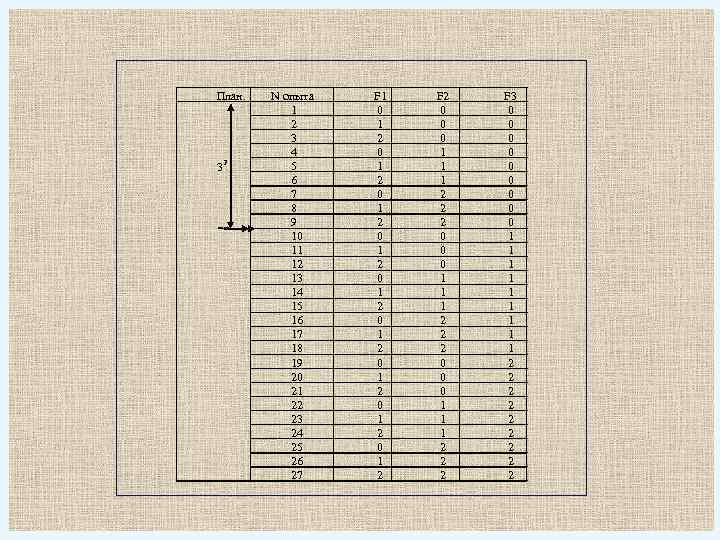План. 32 N опыта 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 F 1 0 1 2 0 1 2 0 1 2 F 2 0 0 0 1 1 1 2 2 2 F 3 0 0 0 0 0 1 1 1 1 1 2 2 2 2 2

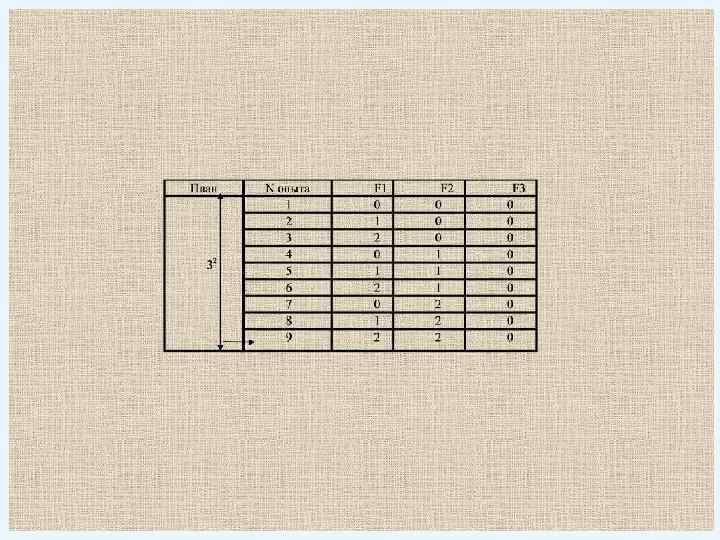
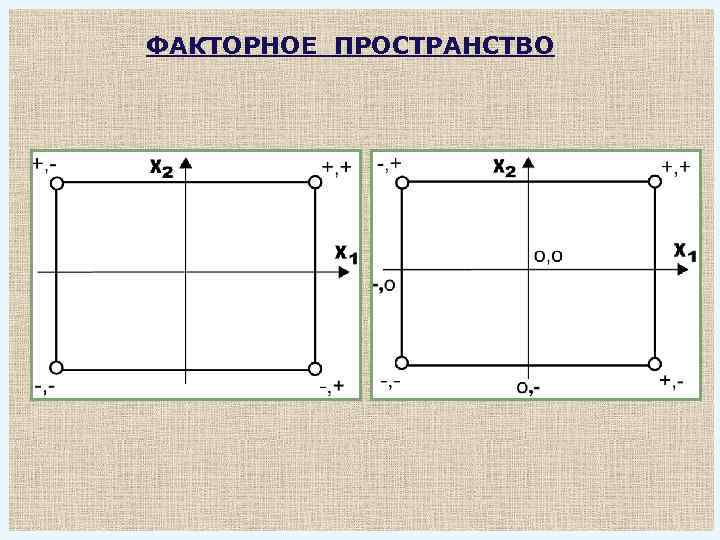ФАКТОРНОЕ ПРОСТРАНСТВО

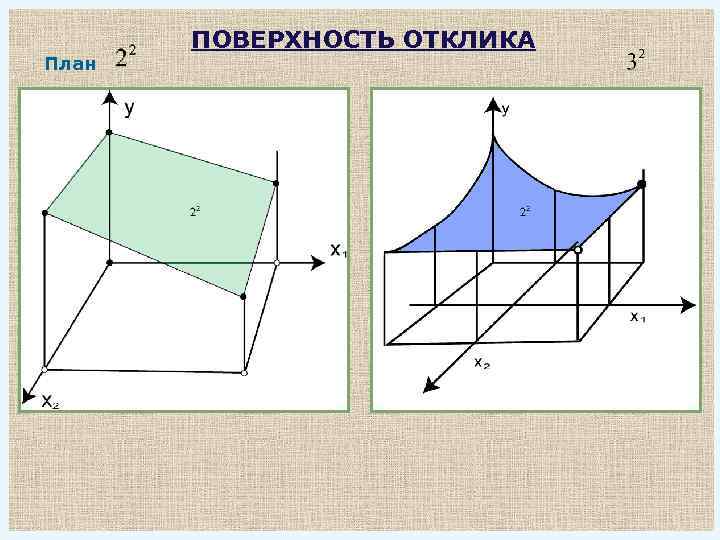План ПОВЕРХНОСТЬ ОТКЛИКА