Чурюмов Александр Юрьевич Организация эксперимента Лекция 2

Чурюмов Александр Юрьевич Организация эксперимента Лекция 2

Виды корреляционной связи • односторонняя связь между случайными переменными. Физически связь может существовать только в одном направлении. • двусторонняя связь (взаимосвязь) между случайными переменными. связи не являются однонаправленными; они могут быть взаимными.

МОДЕЛЬ КОРРЕЛЯЦИОННОГО АНАЛИЗА • ВОЗМОЖНЫЕ КОРРЕЛЯЦИОННЫЕ СВЯЗИ

Основная задача корреляционного анализа – установление тесноты связи между случайными переменными (величинами). Виды корреляционного анализа: – определение парных коэффициентов корреляции (линейная корреляция); – определение коэффициентов частной корреляции (детерминированной); – определение коэффициентов множественной корреляции. Предпосылки корреляционного анализа следующие: – переменные величины должны быть случайными, – случайные величины должны иметь совместное нормальное распределение.

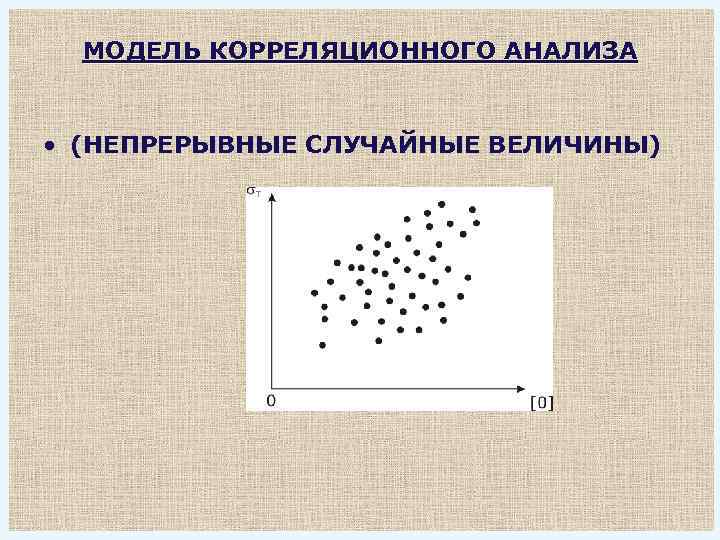МОДЕЛЬ КОРРЕЛЯЦИОННОГО АНАЛИЗА • (НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ)

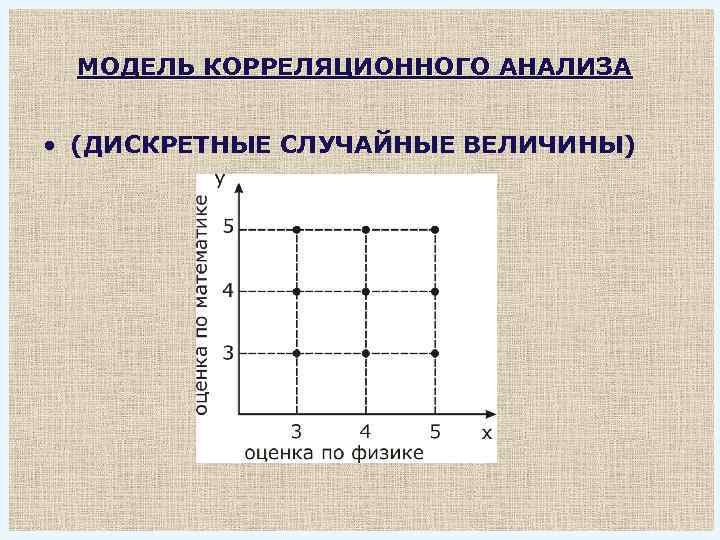МОДЕЛЬ КОРРЕЛЯЦИОННОГО АНАЛИЗА • (ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ)

Коэффициент корреляции 1. Коэффициент корреляции принимает значения на интервале (– 1, + 1). 2. Если коэффициент корреляции положителен, то связь между переменными положительна, и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной другая уменьшается. 3. Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения.

Проверка гипотезы о наличии корреляционной связи Расчетное значение критерия Стьюдента Число степеней свободы k = n – 2 Если расчетное значение | t | t , k, то нулевую гипотезу об отсутствии корреляционной связи следует отвергнуть; переменные считают зависимыми.

Частная корреляция Коэффициент частной корреляции для переменных X 1 и X 2 при фиксированном значении X 3. . Хm выражается через парные коэффициенты линейной корреляции и имеет вид:

Множественная корреляция • Коэффициент множественной корреляции где qm – определитель корреляционной матрицы Qm; qjj – алгебраическое дополнение к элементу rjj. Значимость коэффициента множественной корреляции R проверяют с помощью F -критерия Фишера. Выдвигается нулевая гипотеза: H 0 : R 2 = 0. Статистику F вычисляют по формуле: где l – порядок коэффициента множественной корреляции (l=m-1). Число степеней свободы: k 1 = n – l – 2, k 2 = l. По таблице находится F -критерий для выбранного значения уровня значимости , k 1, k 2. Если F > F , k 1, k 2, то нулевая гипотеза отвергается, коэффициент R считается значимым. Если же F < F , k 1, k 2, то оснований отвергать нулевую гипотезу нет.

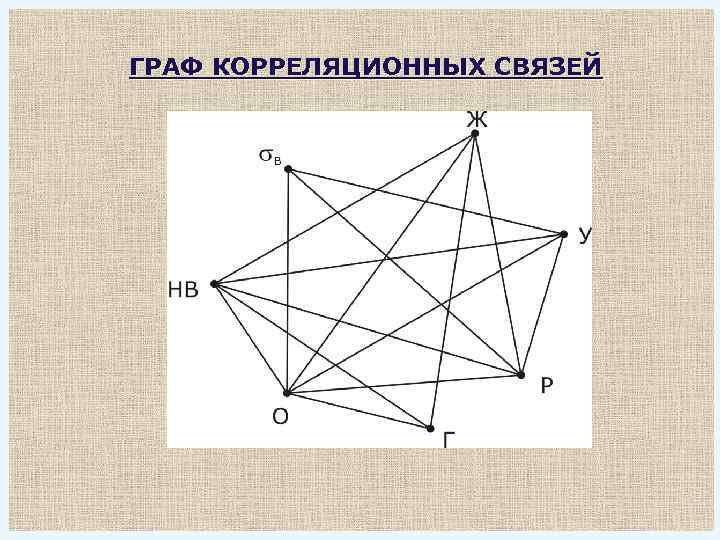ГРАФ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ