Числовые характеристики случайных дискретных величин Лекция 3

Числовые характеристики случайных дискретных величин Лекция № 3

Случайные величины, классификация • Теоретические и экспериментальные исследования показывают, что случайные величины являются существенным элементом любой модели, предназначенной для описания условий и результатов многих экспериментов. • Случайные события - это качественная характеристика случайного результата опыта, но случайный результат можно характеризовать и количественно. Случайная величина – числовая функция от случайного события

Фундаментальные условия определения СС • непредсказуемость исхода, • и устойчивая относительная частота СС. Случайные величины обозначают заглавными буквами всевозможные значения СС

Законы распределения случайной величины • Определение Закон распределения вероятностей случайной величины – соотношение, устанавливающее связь между вероятностями, с которыми случайная величина принимает различные значения и самими возможными значениями случайной величины. • Закон распределения может быть представлен в • • • виде: таблицы, аналитической зависимости графика.

Пример • Вероятности того, что студент сдаст экзамен в сессию по дисциплинам А и Б равны 0. 7 и 0. 9. Составить закон распределения числа экзаменов, которые сдаст студент. • Решение • Случайная величина – число сданных экзаменов 0, 1, 2.

• Определение Ряд распределения - закон распределения вероятностей дискретной случайной величины, заданный в виде таблицы, в первой строке даны значения СВ, а во второй – соответствующие им вероятности. • Пример. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0, 6 и 0, 7. Составить ряд распределения случайной величины Х – числа попаданий после двух выстрелов. Решение Очевидно, что Х может принимать три значения: 0, 1 и 2. Следовательно, ряд распределения имеет вид:

Ряд распределения ДСВ Ряд распределения представляет собой таблицу, в которой указаны все возможные значения случайной величины и их вероятности: хi х1 х2 … хn pi p 1 p 2 … pn ØЗамечание Дискретная случайная величина полностью определяется своим рядом распределения

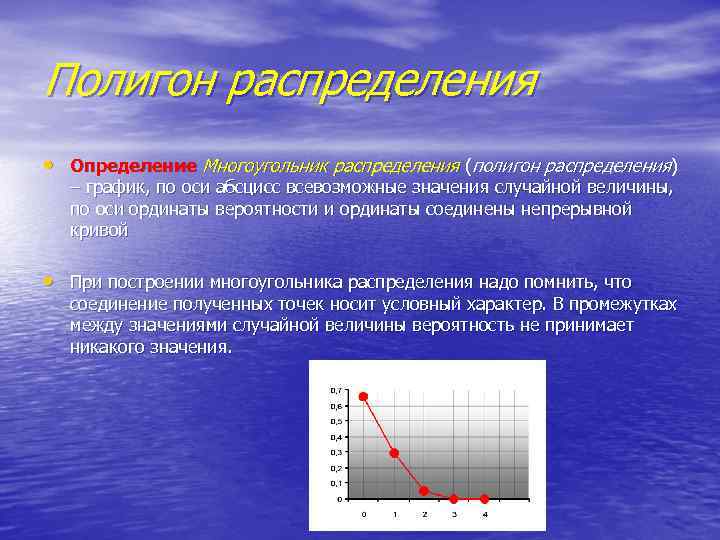Полигон распределения • Определение Многоугольник распределения (полигон распределения) – график, по оси абсцисс всевозможные значения случайной величины, по оси ординаты вероятности и ординаты соединены непрерывной кривой • При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения.

• Определение Многомодальное распределение (двухмодальное) – распределение, имеющее два или несколько максимумов у многоугольника распределения для дискретной случайной величины или на кривой распределения для непрерывной случайной величины. • Определение Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным • Определение Если распределение имеет единственный максимум, то оно унимодальное

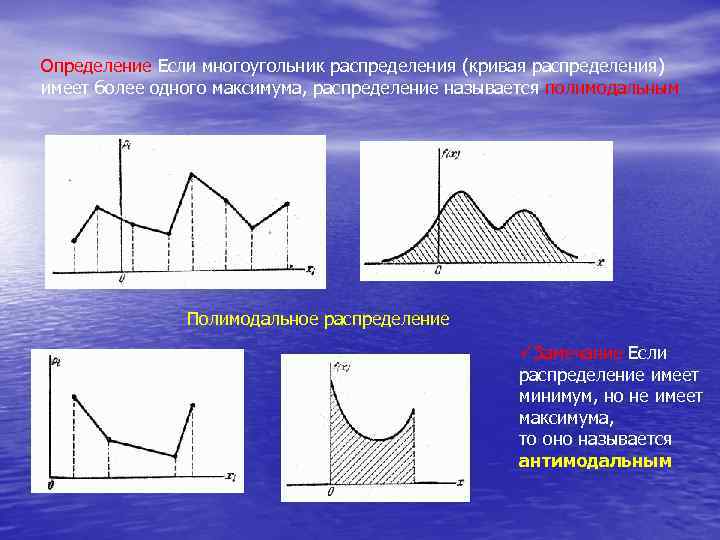Определение Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называется полимодальным Полимодальное распределение üЗамечание Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным

• Теорема (характерное свойство • многоугольника распределения) Сумма ординат многоугольника распределения или сумма всех возможных значений случайной величины всегда равна 1

Классификация случайных величин • два основных класса: • дискретные случайные величины и непрерывные случайные величины • Определение Дискретная случайная величина – • случайная величина, возможные значения которой отделимы друг от друга, принимающая конечное или счетное множество значений Определение Непрерывная случайная величина – случайная величина, возможные значения которой неотделимы друг от друга и непрерывно заполняют некоторый интервал.

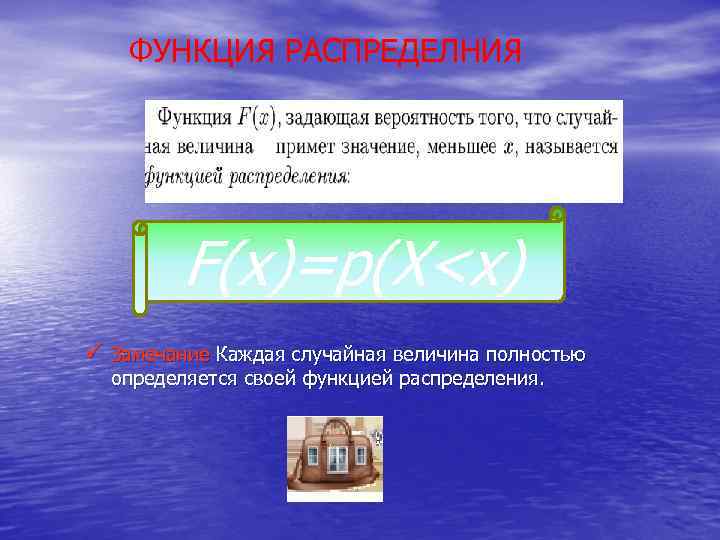ФУНКЦИЯ РАСПРЕДЕЛНИЯ F(x)=p(X

Интегральный закон распределения • Определение Дистрибуанта – функция, выражающая вероятность того, что случайная переменная примет значение меньшее некоторого числа , или функция распределения т. е. üФункция распределения связана с законом распределения и является одной из форм его выражения (интегральный закон распределения).

Функция распределения имеет вид: Суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Высоты ступени равны в каждой точке вероятности соответствующего значения случайной величины. Функция распределения дискретной случайной величины имеет –ступенчата скачки в точках возможных значений случайной величины.

Пример • Пусть X - случайное число очков, выпавших при одном бросании игральной кости • Функция распределения и график функции распределения имеют вид:

Геометрическая интерпретация ФР Рассмотрим случайную величину Х как случайную точку на оси х, которая в результате опыта может принять то или иное положение. Тогда функция распределения есть вероятность того, что эта случайная точка Х окажется левее точки х.

Свойства функции распределения • 1. Функция распределения – неубывающая функция, с ростом X, • она может только возрастать или оставаться постоянной на отдельных участках. Если то

Свойства функции распределения • 1. Функция распределения – неубывающая функция, с ростом X, она может только возрастать или оставаться постоянной на отдельных участках. 2. Функция распределения – неотрицательная функция

3 На минус бесконечности функция распределения равна нулю: 4 На плюс бесконечности функция распределения равна единице:

• 2. Функция распределения – неотрицательная функция • 3. Поведение на концах

Вероятность попадания дискретной случайной величины в заданный интервал • Случайная величина попадет в заданный интервал (a, b) вычисляется по формуле выбирается так, чтобы

. • 4 Вероятность попадания дискретной случайной величины в заданной интервал (a, b) может быть вычислена как разность дистрибутант

Характеристики положения • характеристики положения – числовые характеристики, дающие представление о положении случайной величины на числовой оси. т. е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины. К ним относятся: • Математическое ожидание • Мода • Медиана

Числовые характеристики дискретных случайных величин • Определение Математическое ожидание • дискретной случайной величины - сумма произведений ее возможных значений на соответствующие им вероятности:

• Замечание 1. Математическое ожидание - взвешенное среднее, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов. • Замечание 2. Математическое ожидание не меньше наименьшего возможного значения случайной величины и не больше наибольшего. • Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина • Замечание 4. Математическое ожидание дискретной случайной величины X может не совпадать ни с одним из ее возможных значений.

• Пример 1. Найти математическое ожидание случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных Решение Из условия задачи следует, что Х может принимать значения 1, 2, 3.

üЗамечание Мат. ожидание – число, около которого колеблются значения с. в. и их средние значения по сериям опытов • Определение Отклонение – центрированная с. в. üЗамечание Отклонения противоположных знаков в среднем взаимно погашаются. Поэтому в качестве меры рассеивания берут мат. ожидание квадрата отклонения с. в.

Свойства математического ожидания • 1. Математическое ожидание постоянной равно самой постоянной: М (С) = С Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С·1 = С

• 2. Постоянный множитель можно выносит за знак математического ожидания М (С Х) = С М (Х) Доказательство Если случайная величина Х задана рядом распределения

• 3. Мат. ожидание с. в. определяет положение центра распределения вероятностей • Показатели центра распределения Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, степенные средние, взвешенные средние, центр сгиба, медиана, мода.

4. Мат. ожидание линейно M(ax + bh ) = a M(x )+ b M(h ) 5. Мат. ожидание центрированной с. в. равно нулю Доказательство

• 6. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий M (X Y)=M (X) M (Y) • 7. Математическое ожидание суммы двух случайных величин ( зависимых или независимых ) равно сумме математических ожиданий слагаемых: M (X + Y) = M (X ) + M (Y )

Мода дискретной случайной величины • Мода д. сл. в. — любое её значение, имеющее вероятность, равную максимальной вероятности. Мода д. сл. в. - наиболее вероятное значение. Распределения с одной, двумя или большим числом мод называются соответственно унимодальными (одновершинными), бимодальными или мультимодальными

üЗамечание В общем случае мода и математическое ожидание случайной величины не совпадают. ü В частном случае, когда распределение является симметричным и модальным (т. е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения.

Медиана - такое значение случайной величины, что выполняется условие ü Замечание все три характеристики (математическое ожидание, мода и медиана) не совпадают. Если распределение симметрично и модальное (имеет одну моду), то все они характеризуются одним положением и совпадают.

• Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам üЗамечание В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой

üЗамечание Медиана согласуется с • • интуитивным пониманием «среднего» . К тому же, даже очень «дикие» выбросы изменяют медиану незначительно. Пример если к сотне бедняков (доходы равномерно распределены от 0 до 1 $) добавить одного миллиардера (1 млрд $), среднее сместится от 0, 5 $ до 10 млн $, в то время как медиана — от 0, 5 $ до 0, 505

ü Замечание Медиана определяется для широкого класса распределений (например, для всех непрерывных) ü Замечание в случае неопределённости, естественным образом доопределяется, в то время как математическое ожидание может быть не определено üЗамечание Медиана обычно не определяется для дискретной случайной величины

• Мода — «самое вероятное» значение случайной величины Медиана — «серединное» значение случайной величины Математическое ожидание — «ожидаемое» значение случайной величины

Пример • В одной комнате оказалось 19 бедняков и 1 миллиардер. • • • Каждый кладет на стол деньги — бедняки из кармана, а миллиардер из чемодана. По пять долларов кладет каждый бедняк, а миллиардер — $1 млрд. В сумме получается $1 000 095. Если мы разделим деньги равными долями на 20 человек, то получим $50 004, 75. Это будет среднее арифметическое значение суммы наличных, которая была у всех 20 человек в этой комнате. • Медиана в этом случае будет равна $5 (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). В общем случае медиана это то, сколько принёс с собой средний человек. Наоборот, среднее арифметическое — неподходящая характеристика, так как оно значительно превышает сумму наличных, имеющуюся у среднего человека

Неуникальность значения медиана • Если имеется чётное количество случаев и два • • средних значения различаются, то медианой, по определению, может служить любое число между ними Пример в выборке {1, 2, 3, 4} медианой, по определению, может служить любое число из интервала (2, 3)). • На практике в этом случае чаще всего используют среднее . арифметическое двух средних значений

üЗамечание мода позволяет работать с данными нечисловой природы. • Недостаток: не учитывает поведение распределения в других точках.

• Пример 1. Если ряд распределения дискретной случайной величины Х имеет вид: то мода M 0=2

v. Пример Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида Найдем М(Х) = 49·0, 1 + 50·0, 8 + 51·0, 1 = 50, М(Y) = 0·0, 5 + 100·0, 5 = 50. М(X)=M(Y), но если для Х М(Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением, то значения Y существенно отстоят от М(Y). Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него.

Характеристики рассеивания • Значения наблюдаемых в практике с. в. всегда колеблются около среднего значения. • Это явление называется рассеиванием • величины около ее среднего значения. Основные характеристики рассеивания дисперсия и среднее квадратичное отклонение.

• Определение Дисперсия (рассеяние) случайной величины - математическое ожидание квадрата ее отклонения от ее математического ожидания Дисперсия, как и математическое ожидание являются величиной не случайной

• Пример. • Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных)

• Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друга. • Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения. • Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии

• Дисперсия – сумма квадратов возможных отклонений с. в. от ее среднего значения, взятых с «весовыми» коэффициентами, равными вероятностям соответствующих отклонений • Дисперсия – математическое ожидание квадратов отклонений с. в. от ее среднего значения.

Свойства дисперсии • 1. Дисперсия постоянной величины С равна нулю: D(C)=0 Доказательство

• 2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат Доказательство

• 3. Дисперсия суммы двух независимых • • • случайных величин равна сумме их дисперсий: D(X + Y) = D(X) + D(Y) 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X – Y) = D(X) + D(Y).

• Определение Среднее квадратическое отклонение σ случайной величины Х называется квадратный корень из дисперсии Замечание Чем меньше рассеиваются значения с. в. , тем точнее можно их предсказать.

• Определение Начальным моментом kпорядка сл. величины Х называется математическое ожидание k степени этой величины

• Определение Центральным моментом k - порядка сл. величины Х называется математическое ожидание степени отклонение сл. величины Х от ее мат. ожидания

• Замечание 1 • k=1 - первый начальный момент – • мат. ожидание k=2 - второй центральный момент – дисперсия • Третий центральный момент – служит для характеристики ассиметрии распределения

• Определение Эксцесс число Четвертый центральный момент – служит для характеристики крутости распределения

Свойства эксцесса • 1. Коэффициент эксцесса E>0 положителен, если пик распределения около математического ожидания острый. • 2. Коэффициент эксцесса E<0 отрицателен, • если пик распределения около математического ожидания гладкий. 3. Коэффициент эксцесса принимает значения

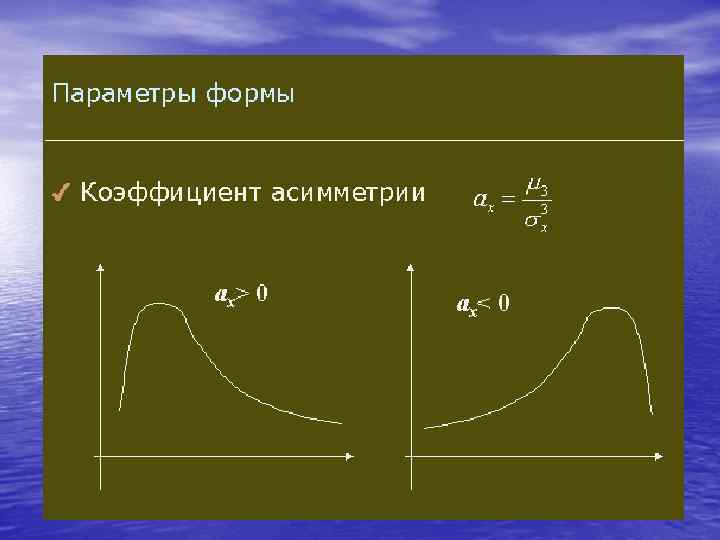
• Определение Коэффициент ассиметрии сл. величины – мера ассиметрии Если А=0, то распределение симметрично относительно мат. ожидания

• В тех случаях, когда при достаточно большом n необходимо вычислить вероятность появления события A не менее m раз и не более k раз, применяют интегральную теорему Муавра-Лапласа

Локальная формула Муавра-Лапласа • Теорема Если число испытаний n достаточно велико, а вероятности p и q не очень близки к нулю ( n > 100 , npq > 20 ), то вероятность можно приближенно найти по формуле Таблица значений функции ϕ (x) приводится в приложениях

• При использовании таблиц необходимо применять приведенные ниже свойства

Интегральная формула Муавра-Лапласа • Теорема В условиях локальной формулы Муавра-Лапласа вероятность , что число успехов m заключено между двумя значениями , можно приближенно найти по интегральной формуле Муавра-Лапласа Таблица значений функции Ф (x) приводится в приложениях

• При использовании таблиц необходимо применять приведенные ниже свойства

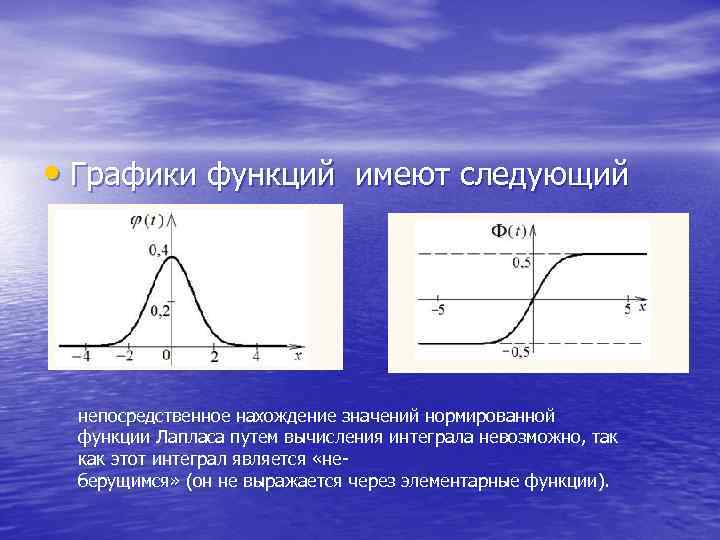• Графики функций имеют следующий вид непосредственное нахождение значений нормированной функции Лапласа путем вычисления интеграла невозможно, так как этот интеграл является «неберущимся» (он не выражается через элементарные функции).

Пример

Пример