Числовые характеристики непрерывных случайных величин Лекция 5

Числовые характеристики непрерывных случайных величин Лекция № 5

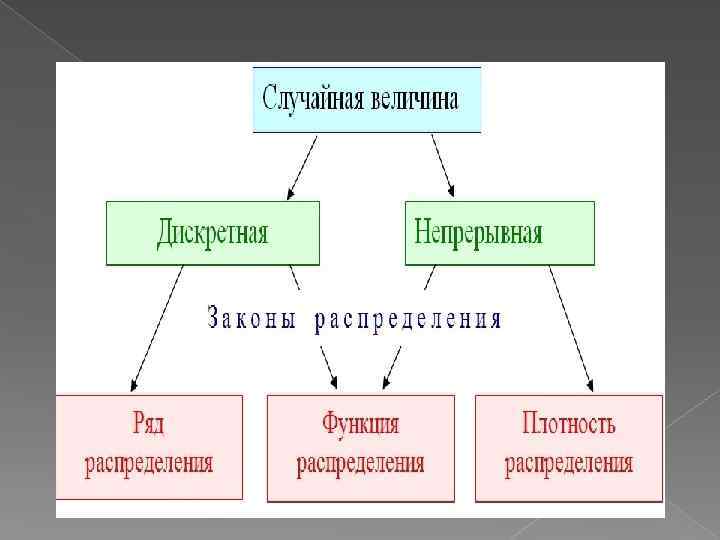
Определение Непрерывная случайная величина (НСВ) - случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.

Определение Функция f(x), равная производной от функции распределения, называется плотностью вероятности случайной величины Х или плотностью распределения. = Плотность вероятности является характеристикой только непрерывных случайных величин

1 Плотность вероятности является неотрицательной функцией (т. к. функция распределения является неубывающей функцией): Плотность вероятности величины. имеет размерность случайной

2 Плотность вероятности является непрерывной функцией. 3 Интеграл в бесконечных пределах от плотности вероятности равен 1: условие нормировки

Функция распределения непрерывной величины Связь интегральной функции распределения и плотности : Числовые характеристики рассчитываются на основе ряда распределения и функции плотности вероятности ØФункция распределения всюду непрерывна. ØПо виду функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси

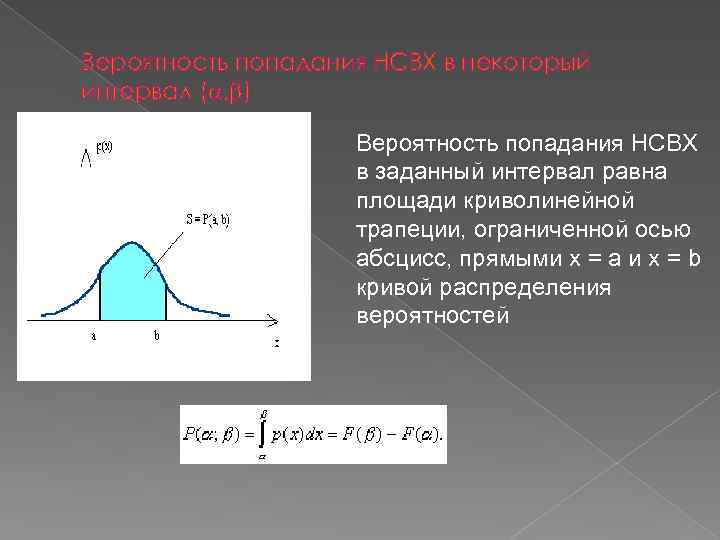Вероятность попадания НСВХ в некоторый интервал ( , ) Вероятность попадания НСВХ в заданный интервал равна площади криволинейной трапеции, ограниченной осью абсцисс, прямыми х = а и х = b кривой распределения вероятностей

Пример НСВХ задана плотностью распределения Найти вероятность попадания в интервал (- ; /4). Решение: Найдем коэффициент а из условия

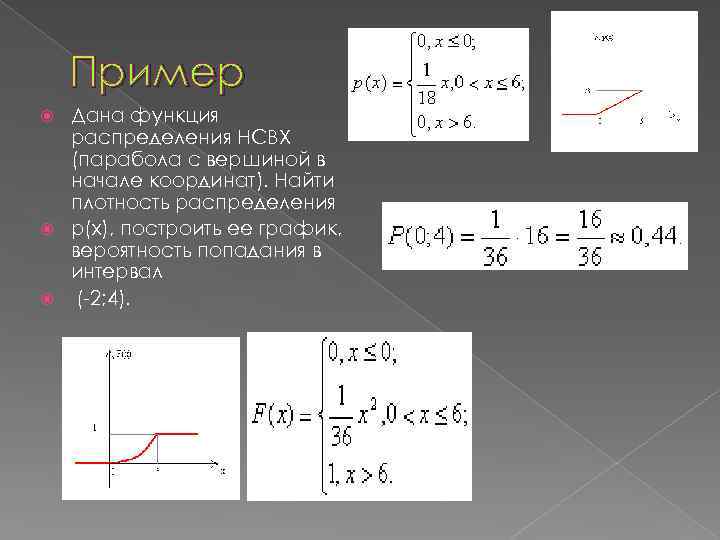Пример Дана функция распределения НСВХ (парабола с вершиной в начале координат). Найти плотность распределения р(х), построить ее график, вероятность попадания в интервал (-2; 4).

Решение: Все значения НСВХ распределены на интервале (0; 6). И графиком функции F(x) является парабола. Найдем k, подставив в уравнение параболы координаты точки (6; 1): 1=36 k, откуда k= 1/36 Тогда интегральная функция имеет вид

Случайная величина Х подчиняется закону распределения Найти величину a и функцию распределения. РЕШЕНИЕ Для нахождения параметра a используем свойство плотности распределения

Функция распределения находится путем интегрирования плотности вероятности: При 0

Числовые характеристики НСВ Определение Математическое ожидание непрерывной случайной величины Х называется определенный интеграл Размерность мат. ожидания совпадает с размерностью случайной величины

Показатели рассеивания определяют степень отклонения от средних величин üДисперсия üСтандартное отклонение üРазмах распределения üКоэффициент асимметрии üЭксцесс

Определение. Дисперсия непрерывной случайной величины - математическое ожидание квадрата ее отклонения

Замечание Дисперсия - характеризует рассеивание случайной величины около ее математического ожидания Замечание Дисперсия обладает свойством аддитивности Замечание Размерность определяется квадратом размерности исходной величины

Смысл математического ожидания и дисперсии остается таким же, как и в случае дискретных случайных величин. Меняется вид формул для их нахождения путем замены:

Замечание Математическое ожидание случайной величины даёт «ее среднее значение» или точку «вокруг которой разбросаны» значения рассматриваемой случайной величины. Замечание дисперсия характеризует «степень разброса» значений случайной величины около её среднего.

Дискретные СВ Непрерывные СВ

Функция распределения непрерывной случайной величины задана выражением: Найти Øвеличину a, Øплотность вероятности, Øвероятность попадания на участок (0. 25 -0. 5), Øматематическое ожидание и дисперсию

1. Так как функция распределения F(x) непрерывна, то при х=1 ax 2=1, следовательно, a=1. 2. Плотность вероятности находится, как производная от функции распределения:

3. Вероятность попадания на заданный участок вычислим двумя способами: с помощью функции распределения и с помощью плотности вероятности. 1 способ. 2 способ

4. Находим математическое ожидание: 5. Находим дисперсию

Показатели центральной тенденции определяют значения около которых группируются случайные величины Мода Медиана

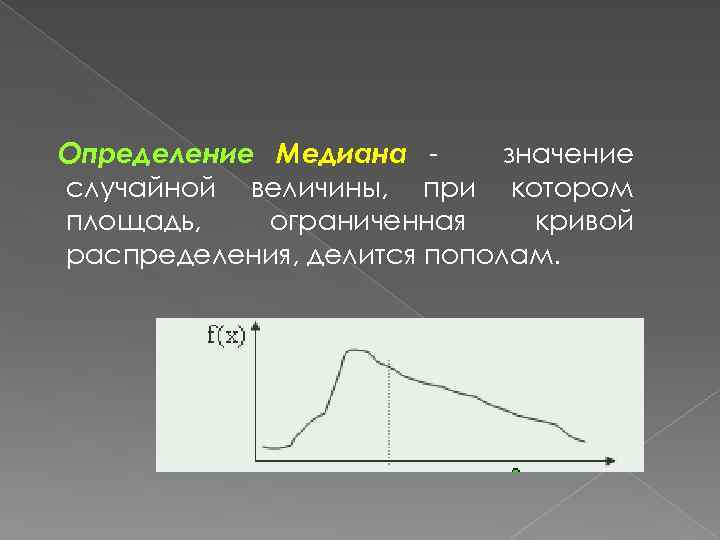Определение Медиана значение случайной величины, при котором площадь, ограниченная кривой распределения, делится пополам.

Определение. Мода М 0 непрерывной случайной величины - значение случайной величины, при которой плотность распределения имеет максимум. Если два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным. Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным

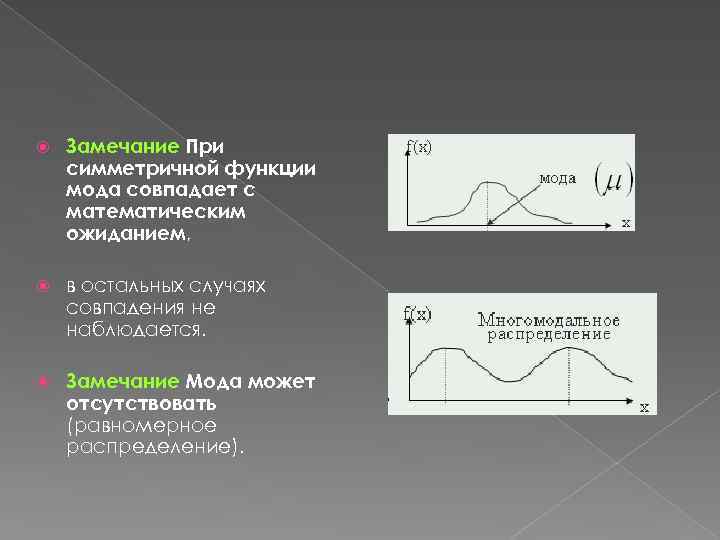Замечание При симметричной функции мода совпадает с математическим ожиданием, в остальных случаях совпадения не наблюдается. Замечание Мода может отсутствовать (равномерное распределение).

Определение. Начальным моментом порядка k случайной величины Х математическое ожидание соответствующих степеней случайной величины, где K - номер момента случайной величины

Определение. Центральным моментом порядка k случайной величины Х называется математическое ожидание величины отклонения степени k

Замечание Центральный момент первого порядка всегда равен нулю, Центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Определение Коэффициент ассиметрии сл. величины Если А=0, то распределение симметрично относительно мат. ожидания

Коэффициент асимметрии - служит для характеристики степени асимметричности ряда или плотности распределения вероятности случайной величины X относительно ее математического ожидания.

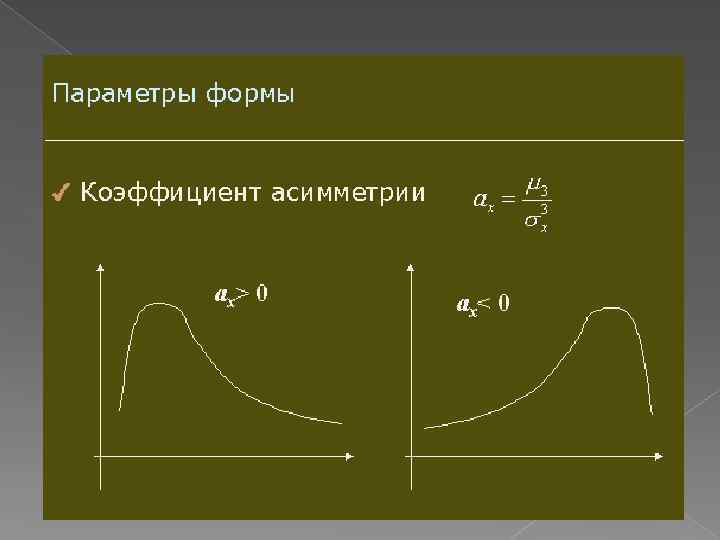
q Замечание Если распределение симметрично, то центральные моменты нечетного порядка, в том числе и коэффициент асимметрии равны нулю q Замечание Коэффициент асимметрии - безразмерная величина зависит от крайних значений случайной величины

Эксцесс – характеристика островершинности ряда или функции плотности распределения. Эксцесс определяется через четвертый центральный момент, безразмерная величина

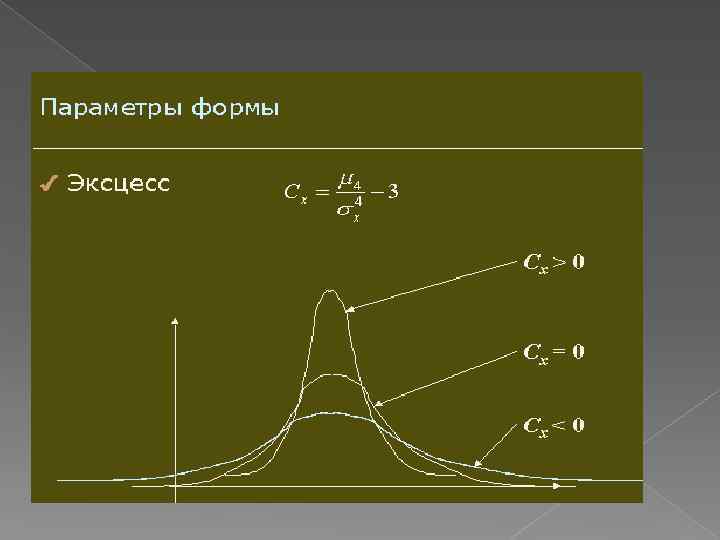
Свойства эксцесса Эксцесс равен нулю для нормального распределения Эксцесс положителен для кривых более остроконечных, по сравнению с нормальной плотностью распределения Эксцесс отрицателен для кривых более плосковершинных по сравнению с нормальной функцией плотности распределения

Основные законы непрерывных случайных величин В теории и практике надежности чаще всего используются следующие законы распределения: равномерный закон распределения нормальный (Гаусса), логарифмически нормальный, Вейбулла, экспоненциальный (показательный)

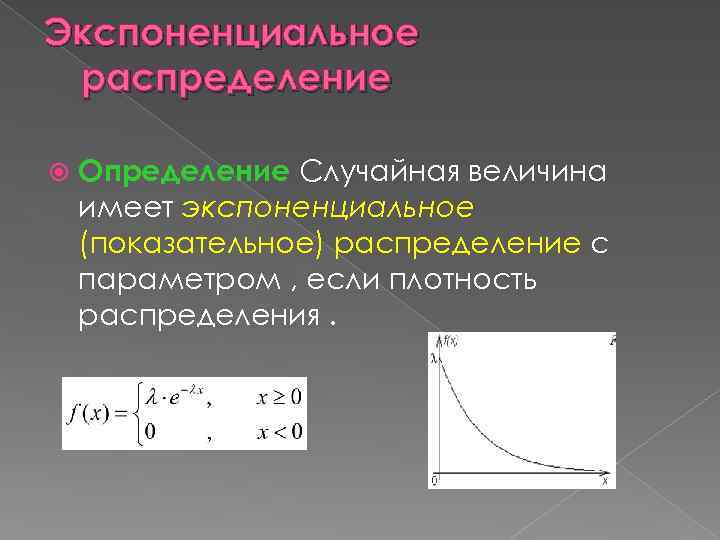Экспоненциальное распределение Определение Случайная величина имеет экспоненциальное (показательное) распределение с параметром , если плотность распределения.

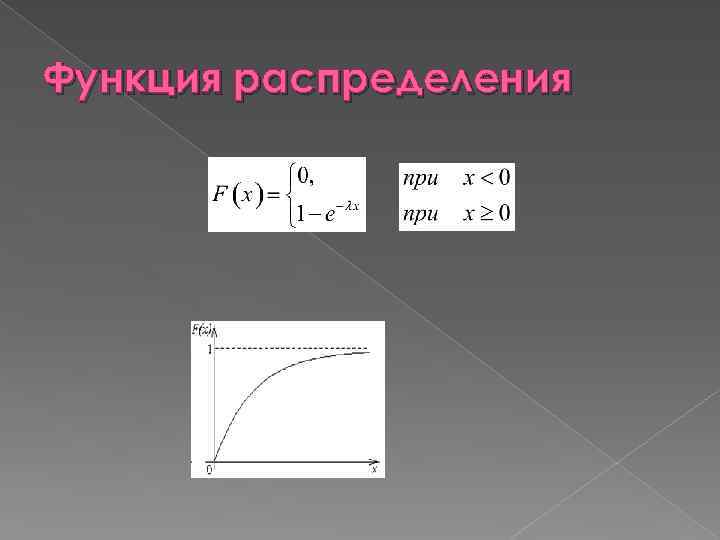Функция распределения

Числовые характеристики экспоненциального распределения • Экспоненциального распределения имеет одинаковое математическое ожидание и среднее квадратичное отклонение.

Замечание Коэффициент ассиметрии равен 2. Замечание Коэффициент эксцесса равен 6. Замечание Медиана равна Вероятность попадания случайной величины в заданный интервал.