Число Комплексное число как расширение понятия числа Действия

Число. Комплексное число, как расширение понятия числа. Действия над комплексными числами.

Число. • Натуральные числа – числа которые употребляются при счете. • Числа целые и дробные, как положительные, так и отрицательные, вместе с числом 0 называются рациональными числами. • Каждое рациональное число может быть представлено в виде отношения p/q, где p и q целые числа.

• Например: 5/7 • Целое число p/1, 6=6/1 • Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей. • Числа, которые представляются бесконечными, но непериодическими десятичными дробями, называются иррациональными числами.

• Совокупность всех рациональных и иррациональных чисел называется множеством действительных (или вещественных) чисел. • Действительные числа упорядочены по величине: для любых x, y имеет место одно из соотношений xy.

• Действительные числа можно изобразить точками числовой оси. • Числовая ось – это бесконечная прямая на которой изображены: 1. Некоторая т. 0 – начало отчета; 2. Указано стрелкой положительное направление; 3. Указан масштаб измерения длин. N 1 -2 0 N 2 1, 5 x

Свойство совокупности действительных чисел • Между двумя произвольными действительными числами найдутся как рациональные, так и иррациональные числа.

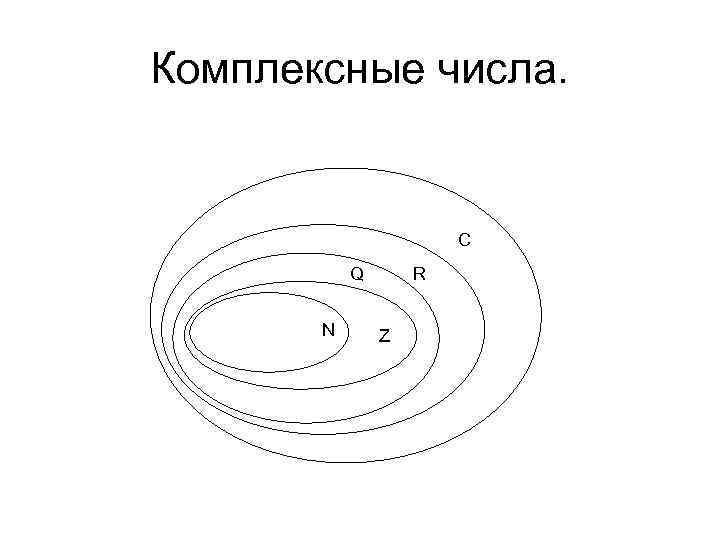Комплексные числа. C Q N R Z

• Комплексным числом z называется выражение вида z=x+iy (алгебраическая форма комплексного числа), где x и y любые действительные числа, а i – мнимая единица, удовлетворяющая условию i 2=-1. • Числа x и y называют соответственно действительной и мнимой частями комплексного числа z и обозначают x = Re z, y = Im z. Пр. z=3+2 i

Комплексные числа z 1= x 1+ iy 1 и z 2=x 2+ iy 2 считаются равными тогда и только тогда(ттогда), когда x 1 =x 2, y 1 = y 2.

• Комплексное число z=x-iy называется сопряженным комплексному числу z=x+iy. • Пр. 3+2 i, 3 -2 i

Действия над комплексными числами. • Пусть даны два комплексных числа z 1= x 1+ iy 1 и z 2=x 2+ iy 2. • Опр. Суммой z 1+ z 2 чисел z 1 и z 2 называется комплексное число z 1+ z 2 = (x 1+ x 2)+ i(y 1 + y 2) Пр.

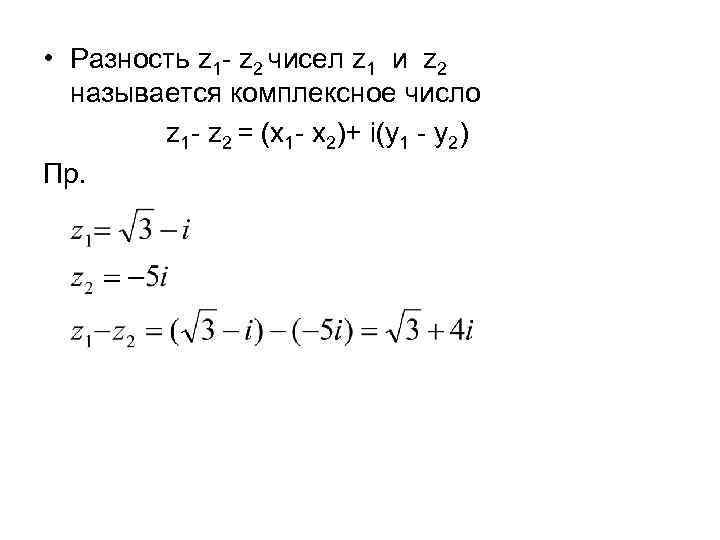• Разность z 1 - z 2 чисел z 1 и z 2 называется комплексное число z 1 - z 2 = (x 1 - x 2)+ i(y 1 - y 2) Пр.

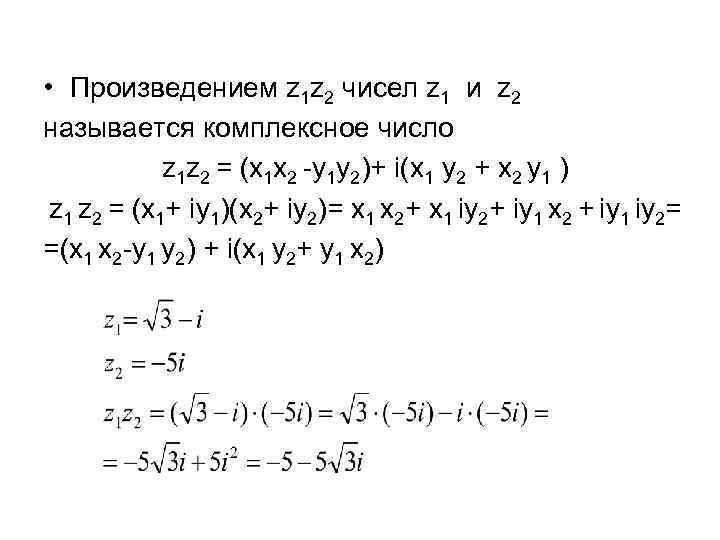• Произведением z 1 z 2 чисел z 1 и z 2 называется комплексное число z 1 z 2 = (x 1 x 2 -y 1 y 2)+ i(x 1 y 2 + x 2 y 1 ) z 1 z 2 = (x 1+ iy 1)(x 2+ iy 2)= x 1 x 2+ x 1 iy 2+ iy 1 x 2 + iy 1 iy 2= =(x 1 x 2 -y 1 y 2) + i(x 1 y 2+ y 1 x 2)

• • • i 2=-1 i 3=-i i 4=1 i 5=i 4 i=i Пр. z 4=(-5 i)4=625 i 4=625

• Частным z 1/z 2 от деления комплексного числа z 1 на комплексное число z 2 называется комплексное число

• Пр.

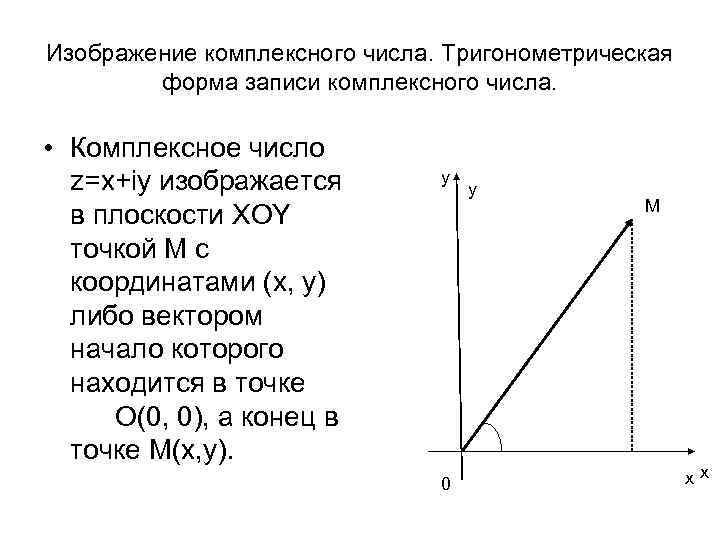Изображение комплексного числа. Тригонометрическая форма записи комплексного числа. • Комплексное число z=x+iy изображается в плоскости XOY точкой М с координатами (x, y) либо вектором начало которого находится в точке О(0, 0), а конец в точке М(x, y). y 0 y М xx

• Длина вектора ОМ называется модулем комплексного числа. • Угол φ, образованный вектором ОМ с осью ОX, называется аргументом комплексного числа z и обозначается φ = Arg z; он определяется не однозначно, а с точностью до слагаемого, кратного 2π: Arg z= arg z +2 kπ (k=0, ± 1, ± 2, . . . ), где arg z есть главное значение Arg z, определяемое условием –π< arg z ≤π, причем

• Опр. Два комплексных числа z 1 и z 2 равны ттогда, когда их модули равны, а их аргументы либо равны, либо отличаются на величину, кратную 2π: |z 1| = | z 2| Arg z 1= Arg z 2 +2 kπ (k=0, ± 1, ± 2, . . . ),

• Любое комплексное число z=x+iy (z≠ 0) можно записать в тригонометрической форме z=ρ(cosφ +i sinφ), где ρ =|z|, φ =Arg z Пр. Записать в тригонометрической форме комплексные числа. y 1, 7 i x

Действия над комплексными числами в тригонометрической форме. z 1=ρ1(cosφ1 +i sinφ1), z 2=ρ2(cosφ2 +i sinφ2) z 1 z 2= ρ1 ρ2[cos ( φ1 +φ2 ) +i sin(φ1 + φ2 )], z 1/ z 2= ρ1 / ρ2[cos ( φ1 -φ2 ) +i sin(φ1 - φ2 )], Возведение комплексного числа z=ρ(cosφ +i sinφ) в натуральную степень n : zn=ρn(cos nφ +i sin nφ)

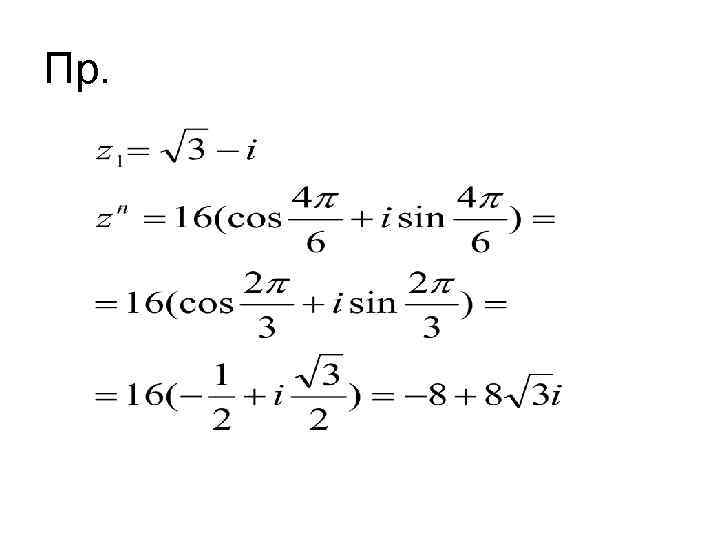Пр.

• Корень n–ой степени из комплексного числа z имеет n различных значений, которые находятся по формуле Муавра.

Пр.

Показательная форма записи комплексного числа. Z=ρe iφ

Переменные • Опр. Переменной величиной называется величина, которая принимает различные числовые значения. • Величина, численные значения которой не меняются, называется постоянной величиной.

• Абсолютной величиной действительного числа x называется неотрицательное действительное число, удовлетворяющее условиям:

Свойства абсолютной величины.

• Опр. Величины, которые сохраняют свое значение в любом явлении, называются абсол