ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Лекция

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Лекция 10 • • • Введение. К решению систем линейных уравнений (СЛУ) сводятся многие практические задачи в химической технологии, например: уравнения материального баланса; уравнения теплового баланса. Кроме того, к решению СЛУ приводят многие другие задачи: численное решение краевых задач для дифференциальных уравнений; моделирование некоторых специальных инженерных задач и др.

1. Основные понятия Система n линейных алгебраических уравнений может быть записана в виде (1. 1) Совокупность коэффициентов этой системы можно записать в виде следующей таблицы (матрицы) (1. 2)

Данная таблица, состоящая из n строк и n столбцов и содержащая n 2 элементов, называется квадратной матрицей порядка n. Используя понятие матрицы А, СЛУ (1. 1) можно записать в матричном виде AX=B, (1. 3) где X и B – вектор-столбцы соответственно неизвестных и правых частей уравнений, то есть X= B= .

Определителем (детерминантом) матрицы А n-го порядка называется число D (иногда обозначают det A), равное (1. 4) . где индексы , , . . . , пробегают все возможные n! перестановок номеров 1, 2, . . . , n; k – число инверсий в данной перестановке. Необходимым и достаточным условием существования единственного решения СЛУ является условие D 0. В случае D=0 матрица называется вырожденной, при этом СЛУ (1. 1) либо не имеет решения, либо имеет их бесчисленное множество. ПРИМЕЧАНИЕ. Матрица A− 1 называется обратной по отношению к квадратной матрице A, если их произведение равно единичной матрице: AA− 1 = A− 1 A= E. Всякая невырожденная матрица A (т. е. с отличным от нуля определителем) имеет обратную. При этом Det A− 1=1/D.

2. Классификация и характеристика методов решения систем линейных уравнений Методы решения СЛУ делятся на две группы: • прямые методы; • итерационные методы. 1) Прямые методы решения СЛУ Прямые методы используют конечные соотношения (формулы) для вычисления неизвестных. Они дают решения после выполнения заранее известного числа итераций. Эти методы сравнительно просты и наиболее универсальны, т. е. пригодны для решения широкого класса линейных систем.

Недостатки прямых методов: • требуют хранения в ОЗУ сразу всей матрицы А (при больших n расходуется много места в памяти); • не учитывают структуру матрицы А; • накапливают погрешности в процессе решения, т. к. вычисления на любом этапе используют результаты предыдущих операций (это особенно опасно для систем большой размерности, так как возрастает общее число операций, а так же для плохо обусловленных систем, очень чувствительных к погрешностям, в силу того, что в них детерминант близок к нулю D≈0).

Поэтому прямые методы используют обычно для сравнительно не больших (n<200) СЛУ с плотной матрицей и не близким к нулю детерминантом. Прямые методы решения иногда называют точными, т. к. решение выражается в виде точных формул через коэффициенты СЛУ. Однако не нужно забывать, что точное решение может быть получено лишь при точных значениях коэффициентов системы, а так же при выполнении вычислений с бесконечным числом разрядов. На практике же, при использовании ЭВМ, вычисления проводятся с ограниченным числом знаков, определяемых разрядностью машины, поэтому неизбежны погрешности в окончательных результатах.

2) Итерационные методы решения СЛУ • Итерационными методами являются методы последовательных приближений. В них, как всегда, нужно задать некоторое приближенное решение – начальное приближение. После этого с помощью некоторого алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения решения с требуемой точностью. • Алгоритмы итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений в них заранее определить трудно. Тем не менее, итерационные методы в ряде случаев предпочтительнее.

Достоинства итерационных методов: • требуют хранения в памяти ЭВМ не всей матрицы системы, а лишь нескольких векторов с n компонентами; • погрешности окончательных результатов не накапливаются, т. к. точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполнен-ных вычислений. • В силу указанных достоинств, итерационные методы особенно полезны в случае большого числа уравнений, а так же плохо обусловленных систем. При этом следует отметить, что сходимость итераций может быть очень медленной. В связи с этим, ищутся эффективные пути ее ускорения. • Итерационные методы полезно использовать для уточнения решений полученных с помощью прямых методов. Такие смешанные алгоритмы обычно довольно эффективны, особенно для плохо обусловленных систем.

3. Методы решения систем линейных уравнений 3. 1. Метод с использованием обратной матрицы В этом случае система записывается в матричном виде AX=B. Тогда, умножая обе части этого векторного уравнения слева на обратную матрицу A− 1, получим X= A− 1 B. Для вычисления обратной матрицы A− 1 могут быть использованы разные методы, например: метод алгебраических дополнений (через алгебраические дополнения и определитель матрицы A); метод Гаусса-Жордано; метод квадратных корней (для симметричной матрицы A) и др. методы. Метод непригоден для решения СЛУ при больших значениях n, если не использовать экономичных схем для вычисления матрицы A− 1 , из-за большого объема вычислений.

3. 2. Метод исключения Гаусса и его модификации Наиболее распространенным среди прямых методов является метод исключения Гаусса и его модификации. Метод основан на приведении матрицы системы к треугольному виду, что достигается путем последовательного исключения неизвестных из уравнений системы. Процесс решения СЛУ состоит из прямого хода метода Гаусса и обратного хода метода Гаусса. 1) Алгоритм прямого хода метода Гаусса: − с помощью первого уравнения исключается переменная x 1 из всех последующих уравнений системы; − затем с помощью второго уравнения исключается x 2 из третьего и всех последующих уравнений; − этот процесс продолжается до тех пор, пока в левой части последнего (nго) уравнения не останется лишь один член с неизвестным xn, т. е. матрица системы будет приведена к треугольному виду. К такому виду можно привести лишь невырожденную матрицу (иначе метод неприменим). 2) Алгоритм обратного хода метода Гаусса: − решая последнее уравнение, находим единственное неизвестное xn; − используя xn, найденное из предыдущего уравнения, находим xn− 1 и т. д. ; − последним находится x 1 из первого уравнения.

3. Пример решения СЛУ Рассмотрим применение метода Гаусса для системы третьего порядка: (3. 1) Прямой ход. Для исключения x 1 из второго уравнения прибавим к нему первое, умноженное на – a 21/a 11. Аналогично, умножив первое на – a 31/a 11 и прибавив к третьему, так же исключим x 1 из третьего уравнения. Получим равносильную СЛУ вида (3. 2) где (i, j=2, 3); (i=2, 3).

Теперь из третьего уравнения системы (3. 2) нужно исключить x 2. Для этого умножим второе уравнение на −a 32'/a 22' и прибавим результат к третьему. Имеем: (3. 3) где Матрица системы (3. 3) имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса. Необходимо заметить, что в процессе исключения неизвестных приходится выполнять операции деления на диагональные коэффициенты и т. д. Поэтому они должны быть отличны от « 0» . Иначе необходимо соответствующим образом переставить уравнения системы. Обратный ход начинается с решения третьего уравнения: x 3=b 3''/a 33''. Используя полученное значение x 3, можно найти х2 из второго уравнения, а затем х1 из первого. Аналогично строится вычислительный алгоритм для линейной системы с произвольным числом n уравнений.

4) Метод Гаусса с выбором главного элемента Одной из модификаций метода Гаусса является схема с выбором главного элемента. Она состоит в том, что требование неравенства нулю диагональных элементов аkk, на которые происходит деление в процессе исключения, заменяется более жестким: из всех оставшихся в k-м столбце элементов нужно выбрать наибольший по модулю элемент, и переставить уравнения так, чтобы этот элемент оказался на месте аkk. Диагональные элементы называются ведущими элементами: ведущий элемент аkk − это коэффициент при k-м неизвестном в k-м уравнении на k-м шаге исключения. Благодаря выбору наибольшего по модулю ведущего элемента, уменьшаются множители, используемые для преобразования уравнений. Метод Гаусса с выбором главного элемента обеспечивает приемлемую точность решения для сравнительно не большого числа (n≤ 100) уравнений. Для плохо обусловленных систем решения полученные по этому методу не надежны. Его целесообразно использовать для решения СЛУ с плотно заполненной матрицей. Все элементы матрицы и правые части СУ находятся в ОЗУ.

3. 3. Итерационные методы 1) Метод уточнения решения Решения, полученные с помощью прямых методов, обычно содержат погрешности, вызванные округлением при выполнении операций на ЭВМ с ограниченным числом разрядов. Рассмотрим один из методов уточнения решения, найденного прямым методом. Пусть с помощью некоторого прямого метода вычислены приближенные значения Подставляя их в левые части исходной системы (1. 1), получим некоторые значения правой части СЛУ отличные от bi (i=1, 2, . . . , n): (3. 4) Обозначим: − погрешности значений неизвестных; − невязки;

Тогда, вычитая каждое уравнение системы (3. 4) из соответствующего уравнения исходной системы (3. 1), с учетом введенных обозначений, получим: (3. 5) Решая эту систему, найдём значения погрешностей которые используем в качестве поправок к решению. Таким образом, следующие приближения неизвестных имеют вид (3. 6) Таким же способом можно найти новые поправки к решению и следующие приближения переменных и т. д. Процесс продолжается до тех пор, пока все очередные значения погрешностей (поправок) не станут достаточно малыми: |εi |≤ E.

Такой процесс уточнения решения представляет фактически итерационный метод решения СЛУ. При этом для нахождения очередного приближения (на каждой итерации) решаются СЛУ вида (3. 5) с одной и той же матрицей, являющейся матрицей исходной системы уравнений, при разных правых частях. В результате каждой итерации получаются новые значения неизвестных. При малом (с заданной погрешностью E) изменении этих значений на 2 -х последовательных итерациях процесс прекращается и происходит вывод значений неизвестных, полученных на последней итерации. Для предотвращения непроизводительных затрат компьютерного времени в случае отсутствия сходимости в алгоритм вводят счётчик числа итераций, при достижении некоторого числа которых счёт прекращается.

2) Метод Гаусса – Зейделя Один из самых простых и распространенных итерационных методов, легко программируемых. Рассмотрим метод на примере СЛУ 3 -го порядка: (3. 7) Положим, что диагональные элементы aii (i=1, 2, 3) отличны от нуля (иначе можно переставить уравнения). Выразим неизвестные x 1, x 2, x 3 соответственно из первого, второго и третьего уравнений системы (3. 7): (3. 8) Зададим некоторые начальные (нулевые) приближения значений неизвестных:

Подставляя начальные приближения в правую часть 1 -го уравнения системы (3. 8) получим новое приближение для x 1: Используя это значение для х1 и приближение для х3, находим из 2 -го уравнения системы (3. 8) первое приближение для х2: И, наконец, используя вычисленные значения находим с помощью 3 -го уравнения системы (3. 8) первое приближение для х3: На этом заканчивается первая итерация решения СЛУ (3. 8).

Используя найденные значения можно по такому же алгоритму провести вторую итерацию, в результате которой будут найдены вторые приближения к решению Приближение с номером k можно представить в виде: Итерационный процесс продолжается до тех пор, пока значения не станут близкими с заданной погрешностью к значениям

Критерий окончания итерационного процесса: где E – заданная допустимая погрешность. Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов, т. е. При этом хотя бы для одного уравнения неравенство должно выполняться строго.

Численное решение дифференциальных уравнений Метод Эйлера может быть применен к решению систем ДУ. Например, дана система 2 -х уравнений 1 -го порядка: c начальными условиями Тогда где

С помощью м. Эйлера можно решить и ДУ высших порядков. В этом случае они должны быть приведены к системе ДУ 1 -го порядка. Например: Обозначим: Получим:

Метод Эйлера Решить ДУ y`=f(x, y) численным методом - это значит для заданной последовательности аргументов x 0, x 1, . . . , xn и числа Y 0 не определяя функцию Y=Y(x), найти такие значения y 1, y 2, . . . , yn, что yi=Y(xi) Y(x 0)=y 0. Таким образом численные методы позволяют вместо нахождения функции Y=Y(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1, называется шагом интегрирования. Метод является сравнительно грубым и применяется в основном для ориентированных расчетов. Однако идеи, положенные в основу м. Эйлера являются исходными для рядов других методов.

Постановка задачи. Задано ДУ 1 -го порядка (1) Требуется найти решение уравнения (1) на отрезке [a, b]. Разобьём отрезок [a, b] на n равных частей, получим последовательность

Выберем к-й участок [xk , xk+1] и проинтегрируем уравнение (1): (2) Если в интеграле подынтегральную функцию принять постоянной на участке [xk, xk+1] и равной начальному значению в точке (xk, yk), то получим

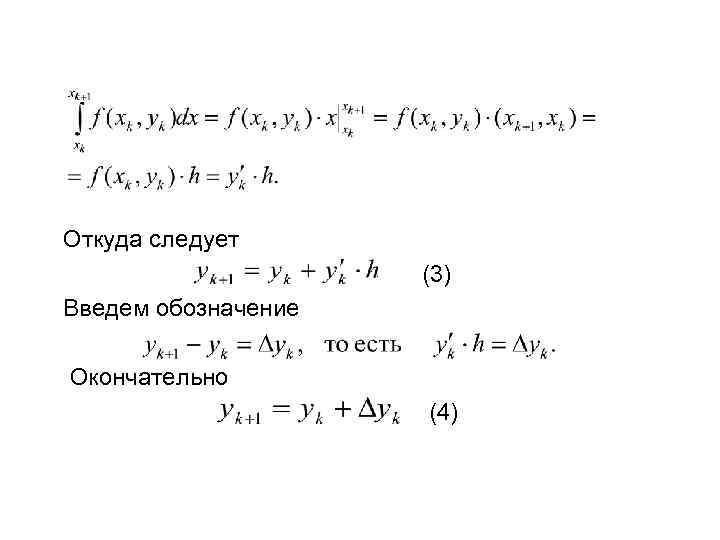Откуда следует (3) Введем обозначение Окончательно (4)

Продолжая этот процесс, и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной её значению в начале участка, получим таблицу решений ДУ (1) на заданном отрезке [a, b]. Равенство (3) означает, что на отрезке [xk, yk] интегральная кривая Y=Y(x) приближённо заменяется прямолинейным отрезком, выходящим из точки Mk(xk, yk) c угловым коэффициентом f(xk, yk). В качестве приближения искомой интегральной кривой получаем ломаную линию с вершинами в точках M 0(x 0, y 0), M 1(x 1, y 1), . . . , Mn(xn, yn). При этом первое звено касается истинной кривой в точке M 0. Чтобы оценить погрешность метода Эйлера на практике применяют т. н. двойной просчет. Для этого сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведётся с шагом h/2.