Численные методы 1 Реальные процессы Модель физическая

Численные методы 1

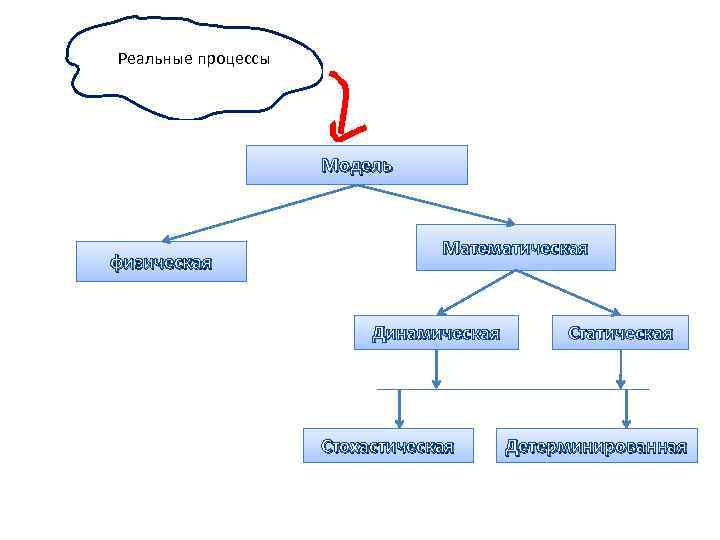Реальные процессы Модель физическая Математическая Динамическая Стохастическая Статическая Детерминированная

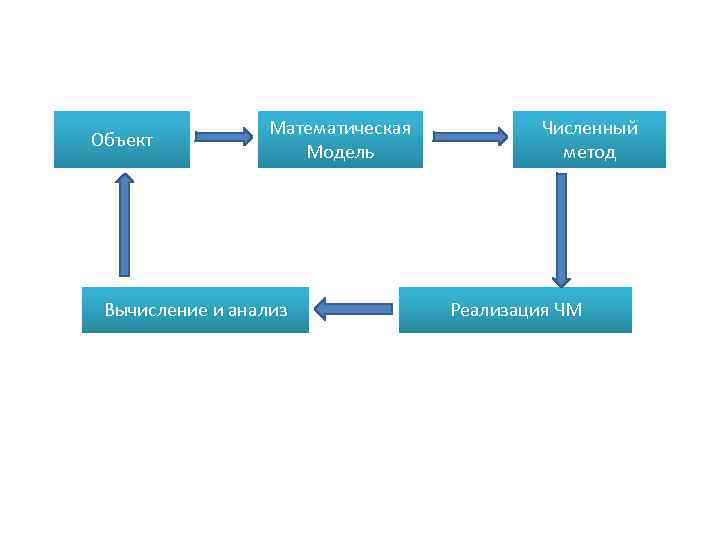Объект Математическая Модель Вычисление и анализ Численный метод Реализация ЧМ

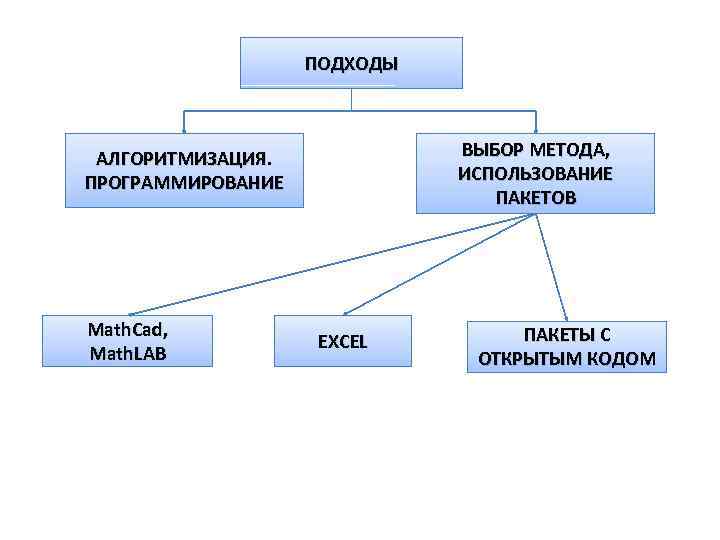ПОДХОДЫ ВЫБОР МЕТОДА, ИСПОЛЬЗОВАНИЕ ПАКЕТОВ АЛГОРИТМИЗАЦИЯ. ПРОГРАММИРОВАНИЕ Math. Cad, Math. LAB EXCEL ПАКЕТЫ С ОТКРЫТЫМ КОДОМ

ЭТАПЫ РЕАЛИЗАЦИИ ЧИСЛЕННЫХ МЕТОДОВ 1. ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ 2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ 3. ВЫБОР МЕТОДА РЕШЕНИЯ 3. 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ 3. 2. ЧИСЛЕННЫЕ МЕТОДЫ 4. РАЗРАБОТКА АЛГОРИТМА 4. 1. ПРОГРАММИРОВАНИЕ 4. 2. ИСПОЛЬЗОВАНИЕ ПАКЕТОВ 5. РЕАЛИЗАЦИЯ, АНАЛИЗ РЕЗУЛЬТАТОВ 5

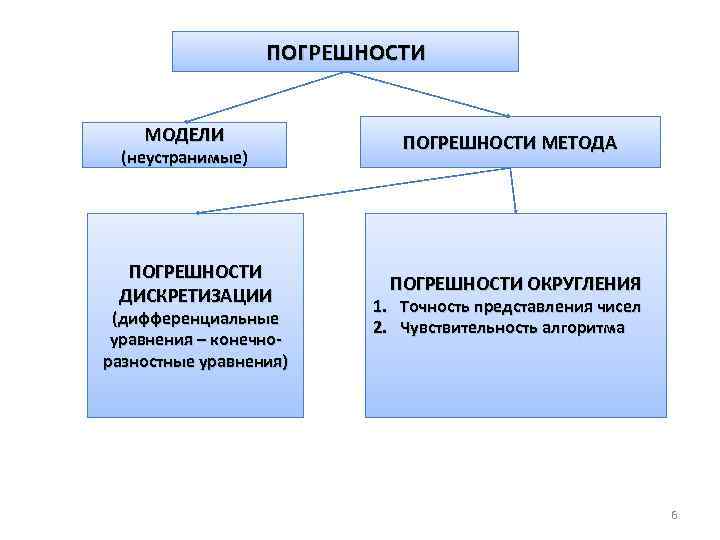ПОГРЕШНОСТИ МОДЕЛИ (неустранимые) ПОГРЕШНОСТИ ДИСКРЕТИЗАЦИИ (дифференциальные уравнения – конечноразностные уравнения) ПОГРЕШНОСТИ МЕТОДА ПОГРЕШНОСТИ ОКРУГЛЕНИЯ 1. Точность представления чисел 2. Чувствительность алгоритма 6

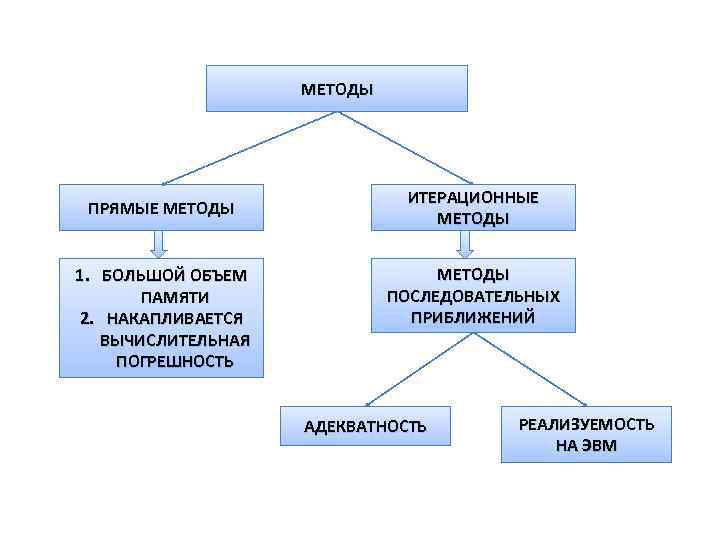МЕТОДЫ ПРЯМЫЕ МЕТОДЫ 1. БОЛЬШОЙ ОБЪЕМ ПАМЯТИ 2. НАКАПЛИВАЕТСЯ ВЫЧИСЛИТЕЛЬНАЯ ПОГРЕШНОСТЬ ИТЕРАЦИОННЫЕ МЕТОДЫ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ АДЕКВАТНОСТЬ РЕАЛИЗУЕМОСТЬ НА ЭВМ

СХОДИМОСТЬ МЕТОДА МЕТОД СХОДИТСЯ, ЕСЛИ ПРИ НЕОГРАНИЧЕННОМ УВЕЛИЧЕНИИ ЧИСЛА УРАВНЕНИЙ РЕШЕНИЕ ДИСКРЕТНОЙ ЗАДАЧИ СТРЕМИТСЯ К РЕШЕНИЮ ИСХОДНОЙ ПОГРЕШНОСТЬ МЕТОДА КОРРЕКТНОСТЬ МЕТОДА – решение существует, единственно и непрерывно зависит от входных данных УСТОЙЧИВОСТЬ - непрерывная зависимость решения от входных данных, равномерная относительно входных данных 8

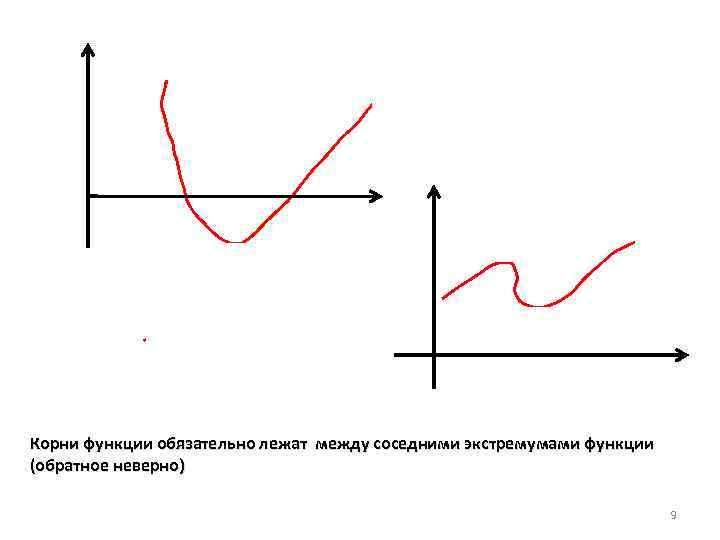Корни функции обязательно лежат между соседними экстремумами функции (обратное неверно) 9

Постановка задачи F(x)=0 Решение осуществляется в два этапа: 1. Отделяются корни, т. е. находят такие отрезки , в которых находится строго один корень 2. Уточняют корень, т. е. находят его значение с заданной точностью. 10

При использовании численных методов, как правило, алгоритм нахождения корня состоит из двух этапов: • Отыскание приближенного значения корня или отрезка на оси абсцисс, его содержащего. • Уточнение приближенного значения корня до некоторой точности. На первом этапе применяется шаговый метод отделения корней, на втором - один из методов уточнения: § метод половинного деления, § метод Ньютона § метод простой итерации. 11

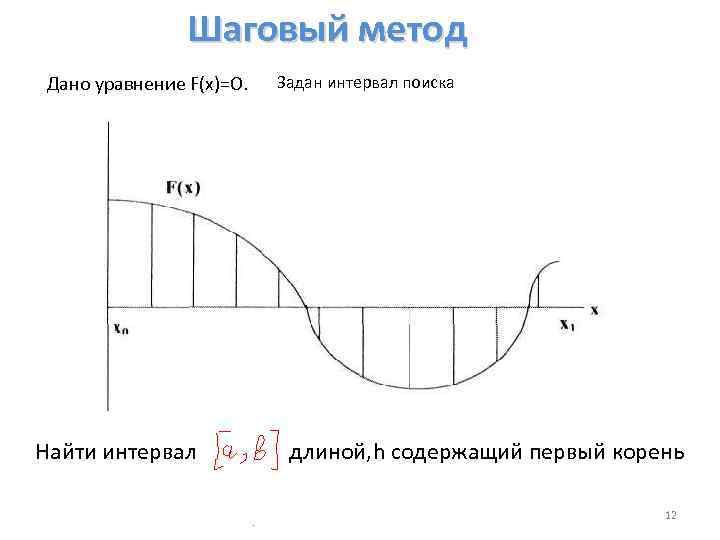Шаговый метод Дано уравнение F(x)=O. Найти интервал Задан интервал поиска длиной, h содержащий первый корень 12

Алгоритм метода: 1. Установить интервал |а, Ь| на начало интервала поиска (а=х ). 2. Определить координату точки b (b=a+h), а также значе ния функции в точках а и b: F(a) и F(b). 3. Проверить условие F(a)*F(b)<0. Если условие не выпол нено передвинуть интервал [а, Ь] на один шаг (а=Ь) и перейти к пункту 2. • Если условие выполнено закончить алгоритм. Решением являются координаты точек а и Ь. Отрезок |а, Ь] содержит корень уравнения, поскольку функция F(x) на его концах имеет разные знаки. 0 13

Дано: Интервал поиска [0, 2] h=0, 3 Найти интервал корня. а b F(a) F(b) 0 0, 3 3 1, 89 нет 0, 3 0, 6 1, 89 0, 96 нет 0, 6 0, 96 0, 21 нет 0, 9 1, 2 0, 21 0, 36 Да

Метод половинного деления Метод основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до тех пор, пока не будет достигнута заданная точность к. 15

Пусть задан отрезок [а, Ь], содержащий один корень уравнения. Этот отрезок может быть предварительно найден с помощью шагового метода. Алгоритм метода : 1. Определить новое приближение корня х в середине отрезка [a, b]: x=(a+b)/2. 2. Найти значения функции в точках а и х: F(a) и F(x). 3. Проверить условие F(a)*F(x)<0. Если условие выполнено, то корень расположен на отрезке [а, х]. В этом случае необходи мо точку b переместить в точку х (Ь=х). Если условие не выпол нено, то корень расположен на отрезке [х, Ь]. В этом случае необ ходимо точку а переместить в точку х (а=х). 4. Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм продолжить до тех пор, пока не будет выполнено усло вие |F(x)I

Дано уравнение Известно, что единственный корень уравнения расположен на отрезке [0, 9; 1, 2]. Требуется уточнить значение корня методом половинного деления с точностью е = 0, 01. a x b F(a) F(x) F(a)*F(x)<0 0, 9 1, 05 1, 2 0, 21 -0, 0975 да 0, 975 1, 05 0, 21 0, 050625 нет 0, 975 1, 0125 1, 05 0, 050625 -0, 02484 да 17

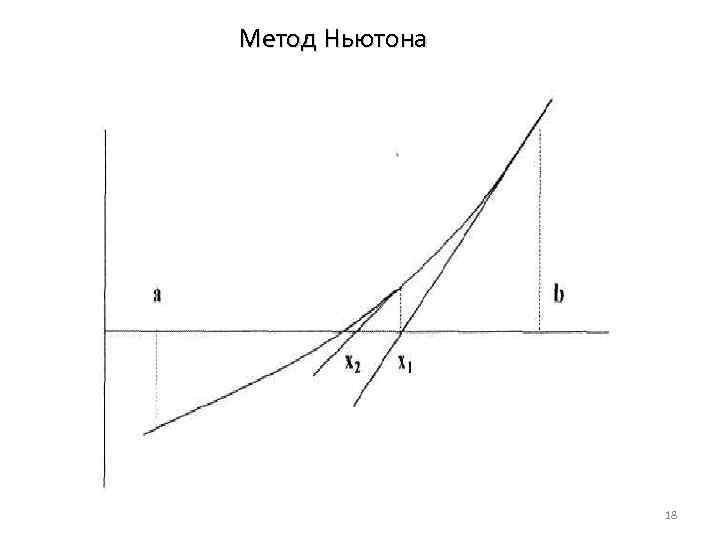Метод Ньютона 18

Задан отрезок [а, Ь], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а, Ь], где значение функции и ее второй производной имеют одинаковые знаки (т. е. выполняется условие F(X 0)*F"(X 0)>0). В точке F(х0) строится касательная к кривой у= F(х) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид: 19

27. 12. 10 ГРУППА 10 СБК 28. 12. 10 ГРУППА 10 КТ 29. 12. 10 ГРУППА 10 ИТД 30. 12. 10 ГРУППА 10 СТ 20

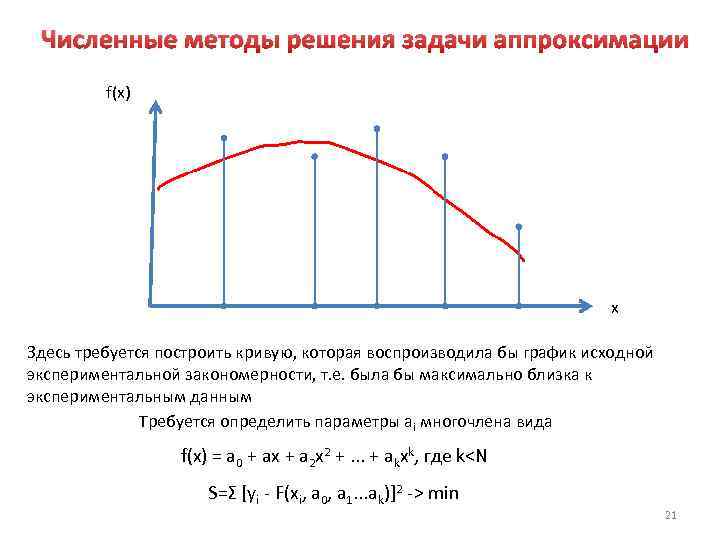Численные методы решения задачи аппроксимации f(x) x Здесь требуется построить кривую, которая воспроизводила бы график исходной экспериментальной закономерности, т. е. была бы максимально близка к экспериментальным данным Требуется определить параметры ai многочлена вида f(x) = a 0 + ax + a 2 x 2 +. . . + akxk, где k min 21

Интерполяция является частным случаем аппроксимации. Это - задача о нахождении такой аналитической функции L(x), которая принимает в точках (узлах) хi заданные значения уi. Иными словами, аппроксимирующая функция в случае интерполяции обязательно проходит через заданные точки. Нахождение значения ф-ции в тех точках, где она не задана 22

Интерполяционная функция L(x) приближенно заменяет исходную f(x), заданную таблично, и проходит через все заданные точки – узлы интерполяции. В связи с интерполяцией рассматриваются три основные проблемы: 1. Выбор интерполяционной функции L(x). 2. Оценка погрешности интерполяции R(x)/ 3. Размещение узлов интерполяции для обеспечения наивысшей возможной точности восстановления функции Чаще всего в качестве интерполяционной функции используется полином nстепени (полиноминальная функция) Это объясняется тем, что полином n-степени, содержащий n+1 параметр и проходящий через все заданные точки - единственный 23

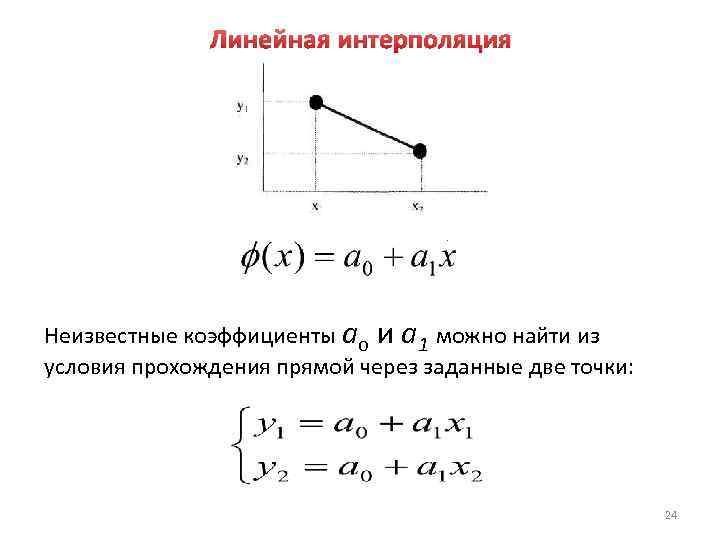Линейная интерполяция Неизвестные коэффициенты ао и а 1 можно найти из условия прохождения прямой через заданные две точки: 24

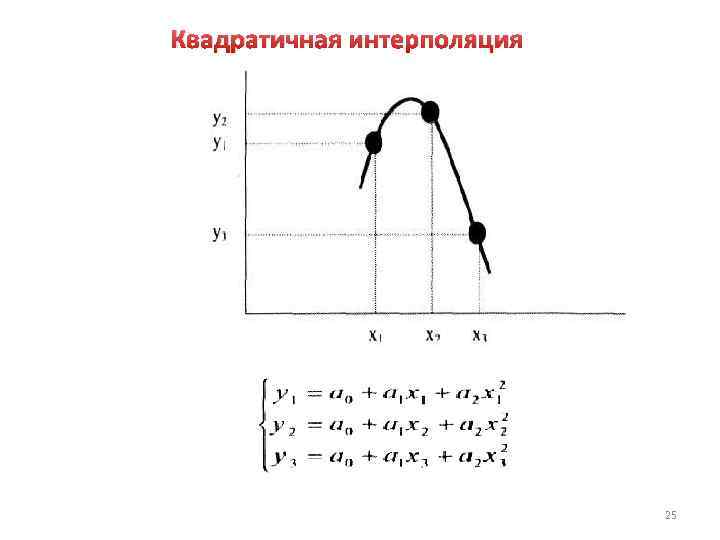Квадратичная интерполяция 25

26

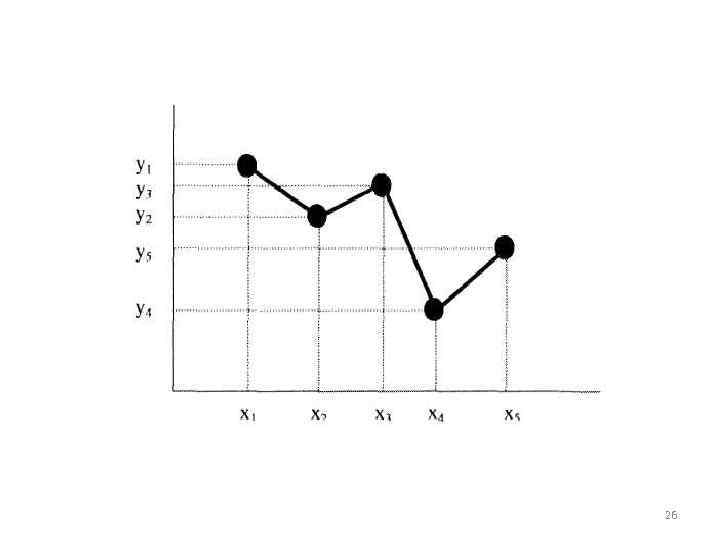
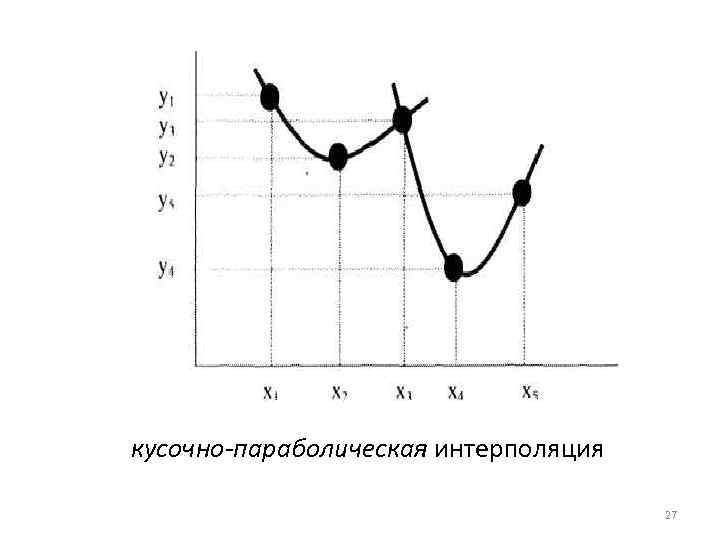кусочно-параболическая интерполяция 27

Общий случай интерполяции. Полином n-й степени. Метод неопределенных коэффициентов m-точек n=m-1 пример 28

Для нахождения неизвестных коэффициентов необходимо построить систему линейных уравнений m-ro порядка из условия прохождения полинома через все т точек: 29

В матричном виде система может быть записана следующим образом: где С - квадратная матрица m x m, составленная из известных координат точек, А - вектор неизвестных коэффициентов, Y— вектор-столбец свободных членов: Можно решить методом Гаусса 30

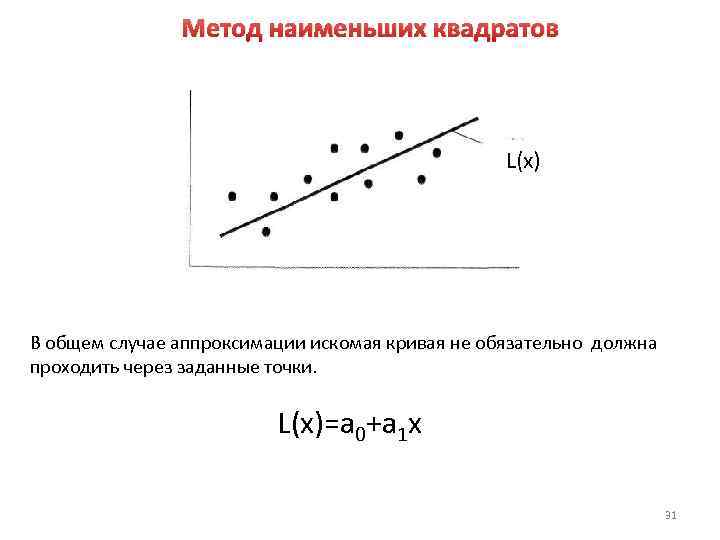Метод наименьших квадратов L(x) В общем случае аппроксимации искомая кривая не обязательно должна проходить через заданные точки. L(x)=a 0+a 1 x 31

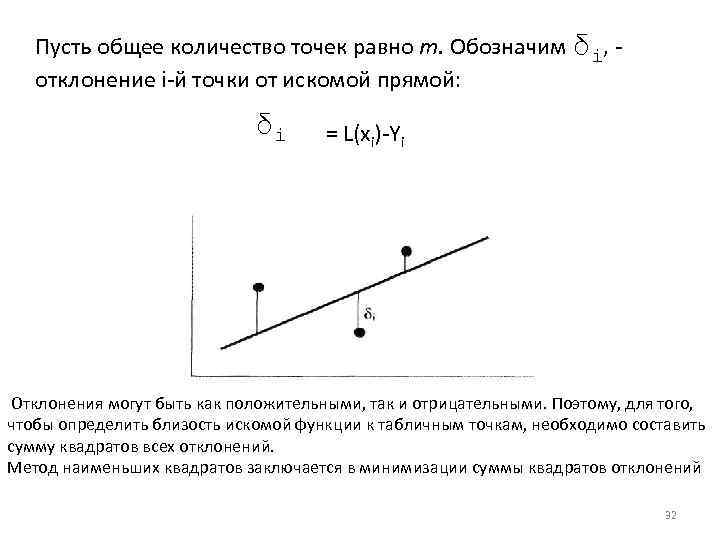Пусть общее количество точек равно т. Обозначим δi, отклонение i-й точки от искомой прямой: δi = L(xi)-Yi Отклонения могут быть как положительными, так и отрицательными. Поэтому, для того, чтобы определить близость искомой функции к табличным точкам, необходимо составить сумму квадратов всех отклонений. Метод наименьших квадратов заключается в минимизации суммы квадратов отклонений 32

В нашем случае эта функция равна: Для нахождения минимума функции S необходимо приравнять нулю ее частные производные. В результате получим систему уравнений: 33

Опуская промежуточные преобразования, получим систему уравнений для нахождения неизвестных коэффициентов a 0 и a 1 Здесь т - количество точек; Суммирование предполагается по всем точкам (i=1, 2, 3…. . . m) 34

Метод наименьших квадратов несложно распространить на общий случай, когда мы будем искать функцию L(x) в виде полинома степени n L(x)=a 0+a 1 x+a 2 x 2+a 3 x 3+……. . anxn B случае аппроксимации всегда справедливо следующее соотношение, связывающее количество исходных точек т и степень искомого полинома: n≤m-1 В случае равенства мы приходим к интерполяции (все отклонения равны нулю). 35

Неизвестные коэффициенты a 0, a 1, a 2, a 3, an находим из условия минимизации суммы квадратов отклонений искомой функции от исходных точек. По аналогии с полиномом первой степени в нашем случае имеем систему уравнений: где Z- квадратная матрица размерностью (n+1)х(n+1), составленная из известных координат точек, столбец свободных членов: А - вектор неизвестных коэффициентов, Y вектор- min 36