Численное решение систем линейных уравнений l Прямой метод

Численное решение систем линейных уравнений l. Прямой метод l. Итерационный метод l. Решение через разложение Холецкого

Численное решение систем линейных уравнений l l Прямые методы – дают алгоритм, по которому можно найти точное решение СЛАУ. Итерационный метод – основан на использовании повторяющегося процесса и позволяет получить решение в результате последовательных приближений.

Прямой метод (метод Гаусса) Алгоритм последовательных исключений Гаусса. Он состоит в преобразовании матрицы А линейной системы к треугольному виду. Т. е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми

Реализация прямого метода

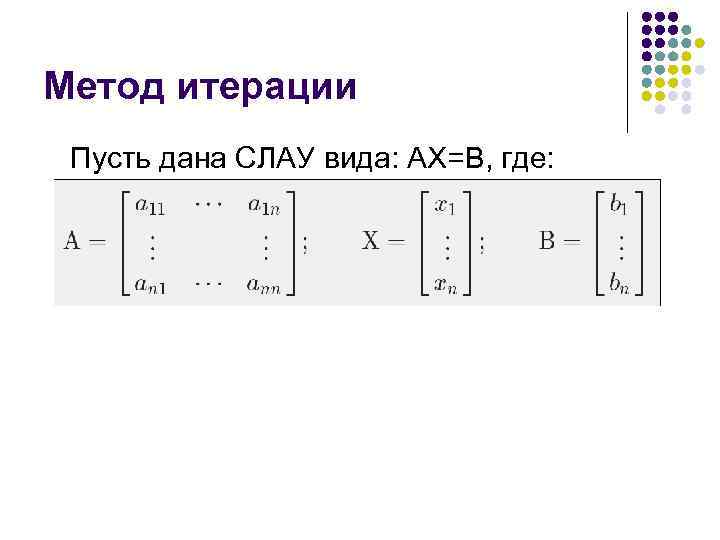Метод итерации Пусть дана СЛАУ вида: AX=B, где:

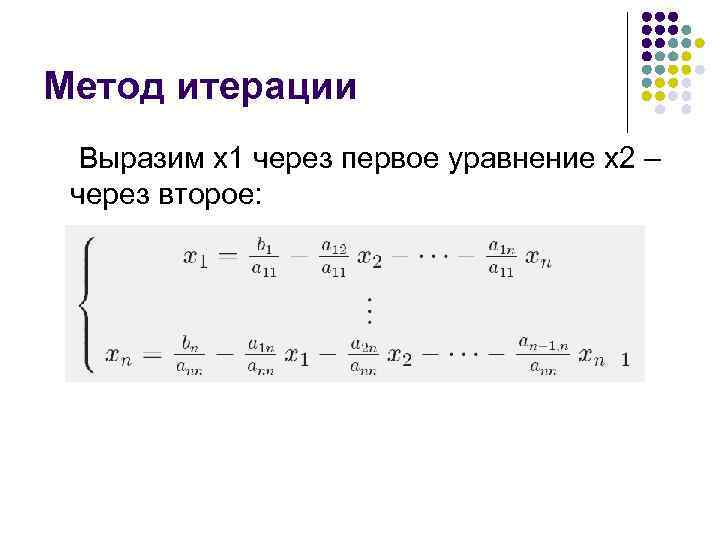Метод итерации Выразим x 1 через первое уравнение x 2 – через второе:

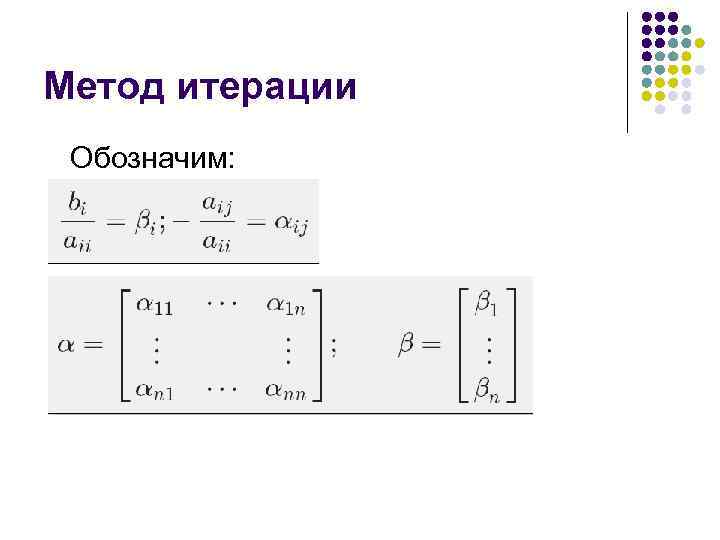Метод итерации Обозначим:

Метод итераций В матричном виде получим: X=β+αx За нулевое приближение примем столбец свободных членов. Нулевое и первое приближение:

Метод итераций В итоге получаем решение:

Реализация метода итераций в Math. Cad

Разложение Холецкого

Разложение Холецкого

Разложение Холецкого Такой способ решения иногда называется – методом квадратных корней. По сравнению с более общими методами, он устойчивее численно и требует примерно вдвое меньше арифметических операций

Реализация Решения СЛАУ с применением разложения Холецкого

Реализация Решения СЛАУ с применением разложения Холецкого Где: trg(L, b) - функция решения верхнетреугольных матриц Ltrg(L, y) – функция решения нижнетреугольных матриц Обе функции пользовательские, применяются для наглядности примера и могут быть заменены lsolve(A, b)