Численное интегрирование Постановка задачи 1 y 0

Численное интегрирование

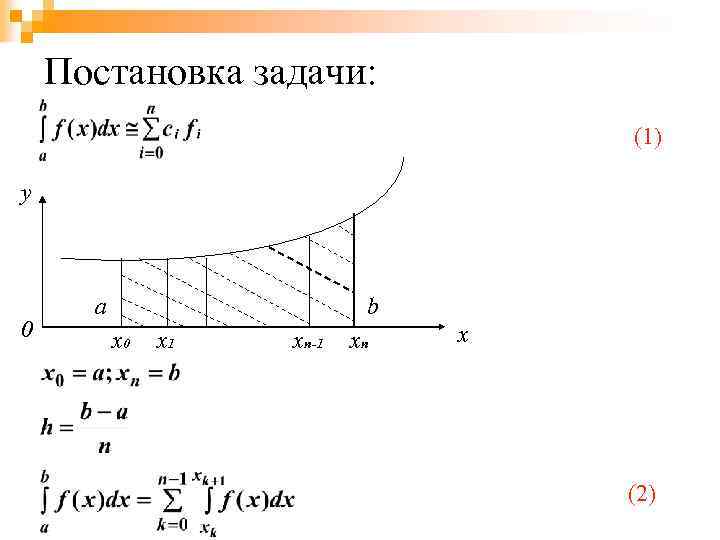Постановка задачи: (1) y 0 a b x 0 x 1 xn-1 xn x (2)

Погрешность численного интегрирования - погрешность вычисления интеграла - погрешность в малом - погрешность вычисления интеграла - погрешность в целом

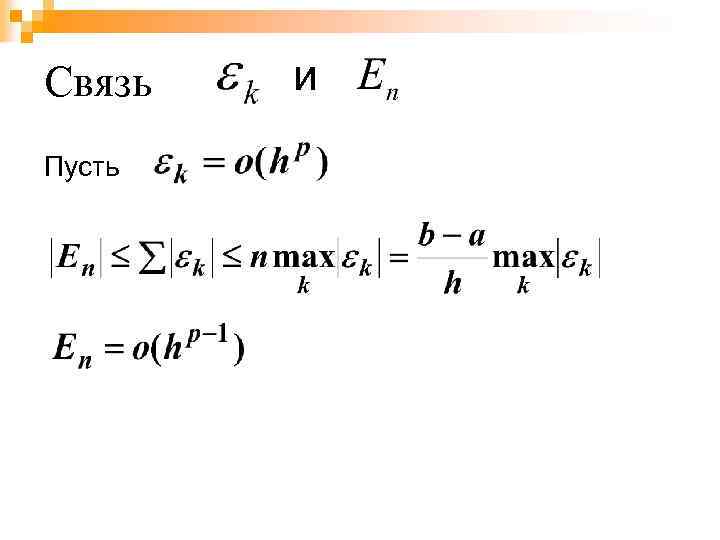Связь Пусть и

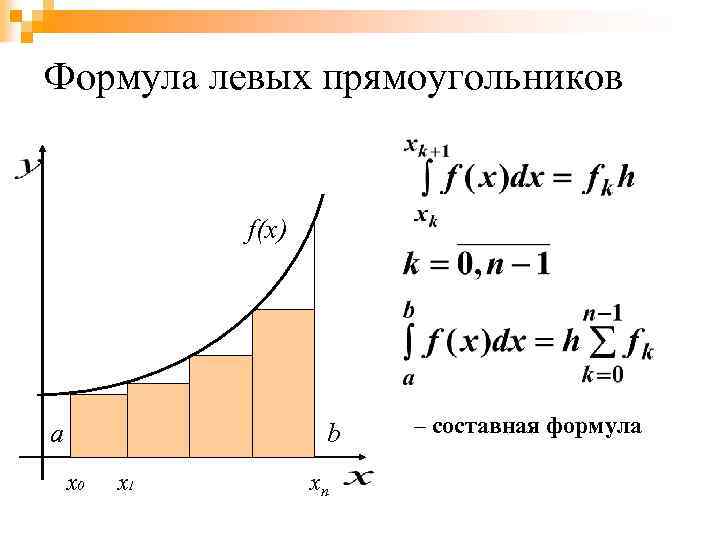Формула левых прямоугольников f(x) a x 0 x 1 b xn – составная формула

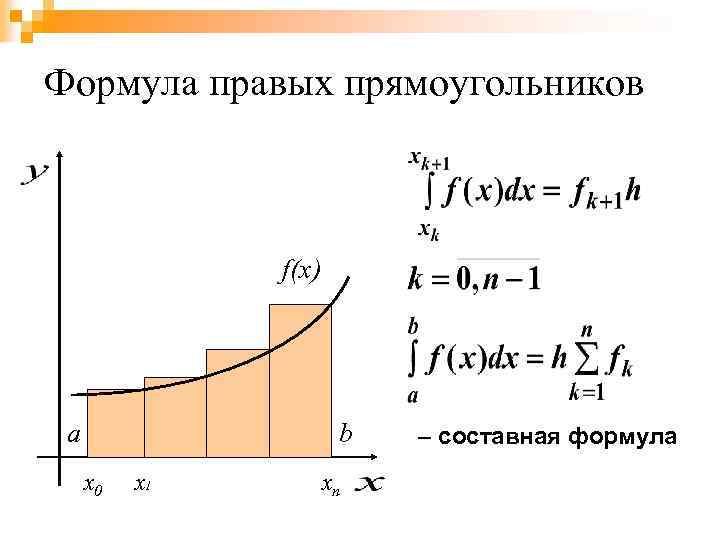Формула правых прямоугольников f(x) a b x 0 x 1 xn – составная формула

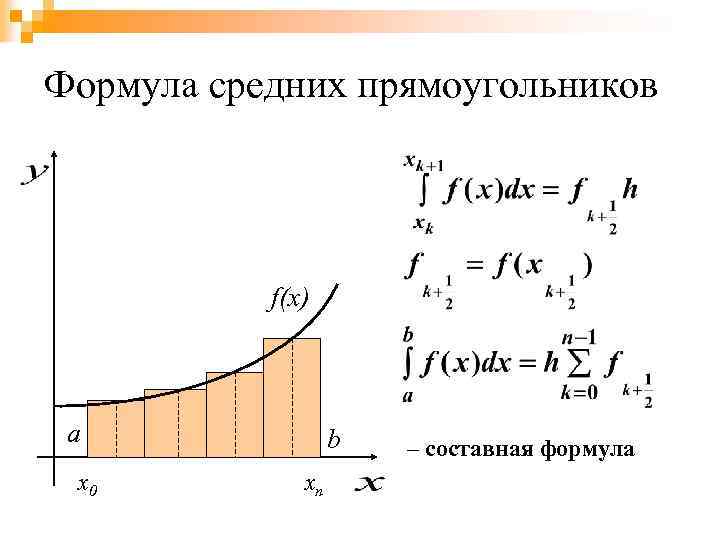Формула средних прямоугольников f(x) a x 0 b xn – составная формула

Погрешность формул средних прямоугольников

Формула трапеции

Погрешность формулы трапеций

Составная формула трапеции

Формула Симпсона

Составная формула Симпсона

Квадратурные формулы Ньютона. Котеса

Квадратурные формулы Ньютона. Котеса (продолжение)

Устойчивость формул численного интегрирования Пусть функция f(x) задана с некоторой погрешностью точное решение

Алгоритм вычисления интеграла с заданной точностью Пусть выбрана квадратурная формула р-ого порядка Ip(h) – приближенное значение интеграла вычисленное по квадратурной формуле р-ого порядка с шагом h 1. выбираем h ( h = 2. вычисляем 3. 4. вычисляем 5. )

Принцип Рунге практического оценивания погрешностей