Числа Фибоначчи
ФИБОНАЧЧИ (Леонардо из Пизы) Fibonacci (Leonardo of Pisa), ок. 1175– 1250 Итальянский математик. Родился в Пизе, стал первым великим математиком Европы позднего Средневековья. В математику его привела практическая потребность установить деловые контакты. Он издавал свои книги по арифметике, алгебре и другим математическим дисциплинам. От мусульманских математиков он узнал о системе цифр, придуманной в Индии и уже принятой в арабском мире, и уверился в ее превосходстве (эти цифры были предшественниками современных арабских цифр).
Фибоначчи в XIII в. вывел особый ряд чисел. Каждое последующее число равно сумме двух предыдущих. Отсчет начинается с 1. 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, ……. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 ……. .
Особенности чисел: 1) Если предыдущее число ряда, разделить на следующее(начиная с 5): 5/8=0, 625 8/13=0, 615 13/21=0, 65 21/34=0, 617 34/55=0, 618 55/89=0, 617 89/144=0, 618 144/233=0, 618 233/377=0, 618
2) Если предыдущее число ряда, разделить на число через 1 (начиная с 5): 5/13=0, 384 8/21=0, 380 13/34=0, 382 21/55=0, 381 34/89=0, 382 55/144=0, 381 89/233=0, 381 144/377=0, 381 0, 382
3) Если взять 2 соседних числа и разделить следующее на предыдущее(начиная с 5): 5/3=1, 666 8/5=1, 6 13/8=1, 625 21/13=1, 615 34/21=1, 619 55/34=1, 617 89/55=1, 618 144/89=1, 617 233/144=1, 618 377/233=1, 618
4) Если любое число из последовательности разделить на позапрошлое число (начиная с 5): 5/2=2, 5 8/3=2, 666 13/5=2, 6 21/8=2, 625 34/13=2, 615 55/21=2, 619 89/34=2, 617 144/55=2, 618 233/89=2, 617 377/144=2, 618
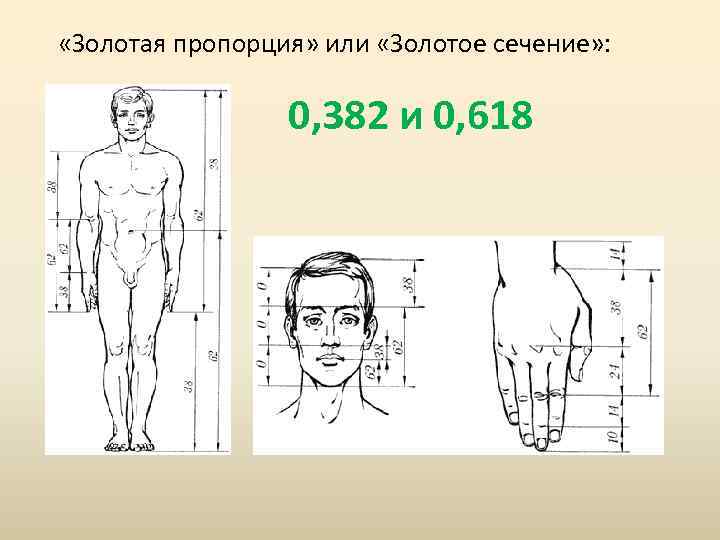
«Золотая пропорция» или «Золотое сечение» : 0, 382 и 0, 618
Николай Николаевич Воробьёв (18 сентября 1925, Ленинград — 1995) Советский математик, специалист в области алгебры, математической логики и теории вероятностей, основатель советской школы в области теории игр.
Теорема Н. Н. Воробьева о поиске максимального значение функции кратчайшим путем.
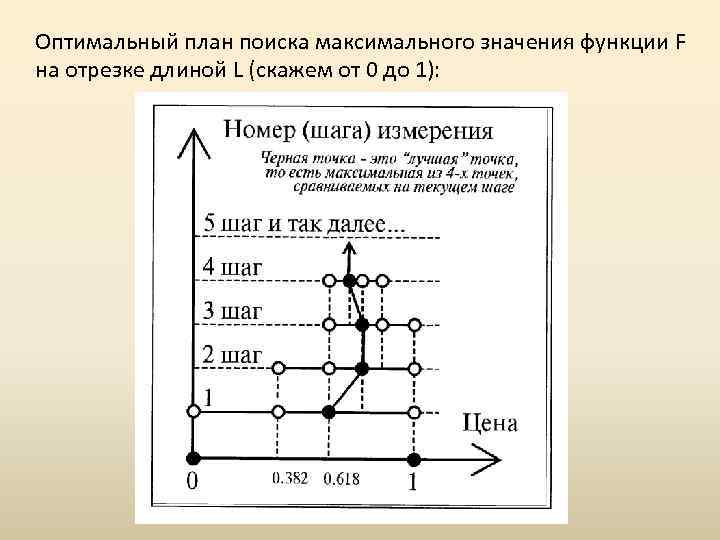
Оптимальный план поиска максимального значения функции F на отрезке длиной L (скажем от 0 до 1):
1. Функция F должна быть гладкой и монотонной, т. е. без перегибов. 2. Известна Fmax, т. е. Xmax, а значит нам известен диапазон цены. 3. Должна быть определена абсолютная погрешность, которую мы считаем приемлемой при нахождении оптимальной цены. По ней можно определить и количество шагов(испытаний).
4. Определено количество шагов, т. е. точность, с которой мы хотим найти оптимальный аргумент X. 5. Делим тестирующий отрезок « 0 -1» на три части двумя внутренними точками, отстоящими от его левого края « 0» на расстояния 0, 382 и 0, 618. 6. Сравниваем значения F в точках 0, 382 и 0, 618 – на одной из них F будет больше. Точку с большим значением F назовем «лучшей» . Найдена «лучшая» точка.
7. Далее строим следующий шаг: к рассмотрению принимаем два целых соседних отрезка(справа и слева от «лучшей» точки). 8. Суммарный отрезок делим еще одной точкой в пропорции 0, 382; новую точку деления отложим от того края суммарного отрезка, который находится дальше от «лучшей» точки. 10. Из двух новых точек ищем лучшую, выбираем два отрезка вокруг нее, делим еще одной и вновь переходим к следующему шагу…. . 9. Внутри суммарного отрезка у нас снова две точки, которые делят общий отрезок тоже в пропорциях 0, 382 и 0, 618.
ИТОГ: за определенное количество испытаний будет найдена оптимальная цена с приемлемой погрешностью.
Спасибо за просмотр!
Скачать презентацию Числа Фибоначчи ФИБОНАЧЧИ Леонардо из Пизы Fibonacci
Числа Фибоначчи.ppt