Chi-square test or 2 test c What

Chi-square test or 2 test c

What if we are interested in seeing if my “crazy” crazy dice are considered “fair”? What can I do?

Chi-square test • Used to test the counts of categorical data • Three types – Goodness of fit (univariate) – Independence (bivariate) – Homogeneity (univariate with two samples)

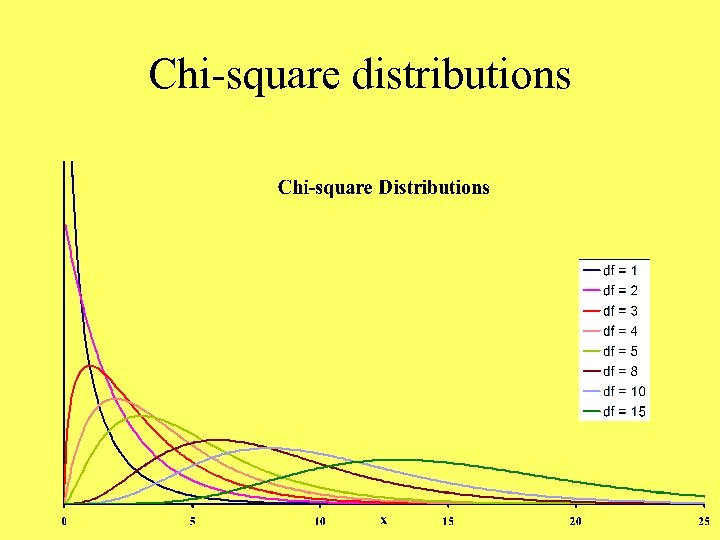Chi-square distributions

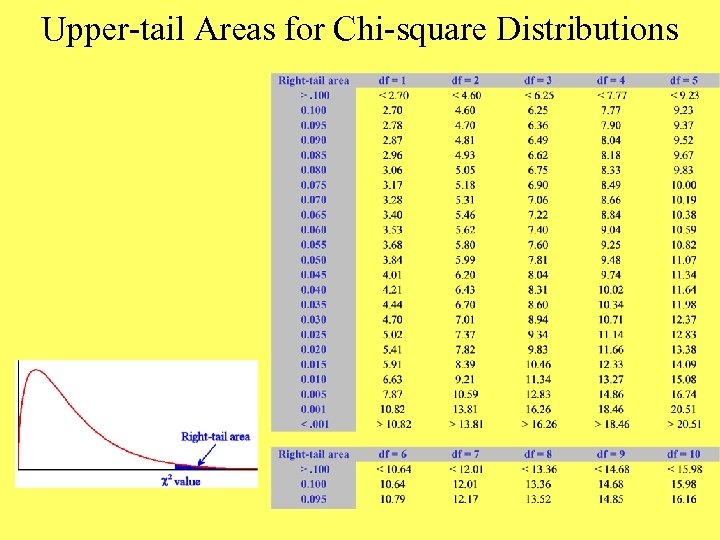Upper-tail Areas for Chi-square Distributions

2 c • • distribution Different df have different curves Skewed right Cannot take on negative values As df increases, curve shifts toward right & becomes more like a normal curve • Each curve has a mode at df-2 and a mean at df

c 2 assumptions • SRS – reasonably random sample • Have counts of categorical data & we expect each category to happen atthese Combine together: least once All expected • Sample size – to insure that the are at counts sample size is large enough weleast 5. should expect at least five in each category. ***Be sure to list expected counts!!

2 c formula

2 c Goodness of fit test Based data • Uses univariateon df – (one sample, one variable) of categories - 1 df = number • Want to see how well the observed counts “fit” what we expect the counts to be • Use c 2 cdf function on the calculator to find p-values

Let’s test our dice!

Hypotheses – written in words H 0: proportions are equal Ha: at least one proportion is not the same Be sure to write in context!

Does your zodiac sign determine how successful you will be? Fortune magazine collected the zodiac signs of 256 heads of the largest 400 companies. Is there sufficient evidence to claim that successful people are more likely to be born under some signs than others? Aries 23 Libra 18 Leo 20 Taurus 20 Scorpio 21 Virgo 19 Gemini 18 Sagittarius 19 Aquarius 24 Cancer 23 Capricorn Pisces 29 22 I would expect CEOs to be equally born under all signs. So 256/12 = 21. 333333 Since there are 12 signs – How many would you 1 = 11 in each sign if there were df = 12 – expect no difference between them? How many degrees of freedom?

Assumptions: • Have a random sample of CEO’s • All expected counts are greater than 5. (I expect 21. 33 CEO’s to be born in each sign. ) H 0: The proportions of CEO’s born under each sign are the same. Ha: At least one of the proportion of CEO’s born under each sign is different.

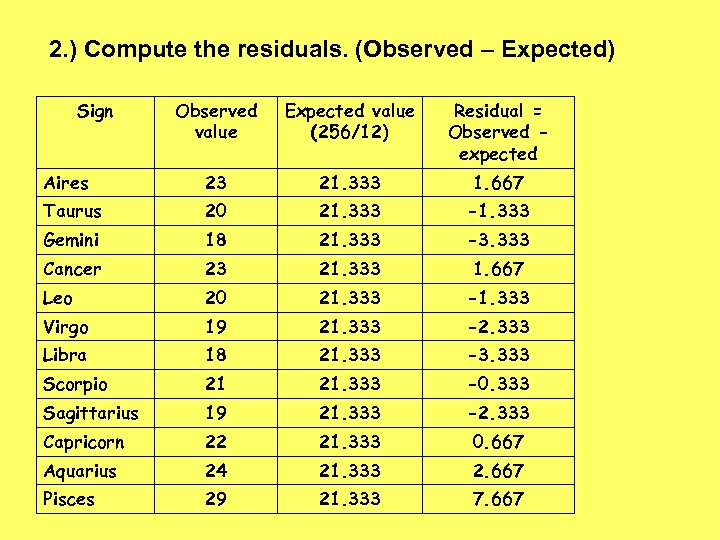2. ) Compute the residuals. (Observed – Expected) Sign Observed value Expected value (256/12) Residual = Observed expected Aires 23 21. 333 1. 667 Taurus 20 21. 333 -1. 333 Gemini 18 21. 333 -3. 333 Cancer 23 21. 333 1. 667 Leo 20 21. 333 -1. 333 Virgo 19 21. 333 -2. 333 Libra 18 21. 333 -3. 333 Scorpio 21 21. 333 -0. 333 Sagittarius 19 21. 333 -2. 333 Capricorn 22 21. 333 0. 667 Aquarius 24 21. 333 2. 667 Pisces 29 21. 333 7. 667

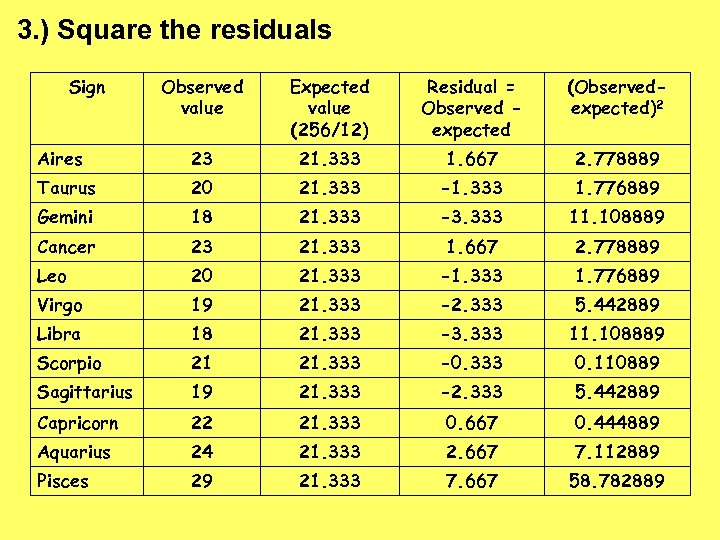3. ) Square the residuals Sign Observed value Expected value (256/12) Residual = Observed expected (Observedexpected)2 Aires 23 21. 333 1. 667 2. 778889 Taurus 20 21. 333 -1. 333 1. 776889 Gemini 18 21. 333 -3. 333 11. 108889 Cancer 23 21. 333 1. 667 2. 778889 Leo 20 21. 333 -1. 333 1. 776889 Virgo 19 21. 333 -2. 333 5. 442889 Libra 18 21. 333 -3. 333 11. 108889 Scorpio 21 21. 333 -0. 333 0. 110889 Sagittarius 19 21. 333 -2. 333 5. 442889 Capricorn 22 21. 333 0. 667 0. 444889 Aquarius 24 21. 333 2. 667 7. 112889 Pisces 29 21. 333 7. 667 58. 782889

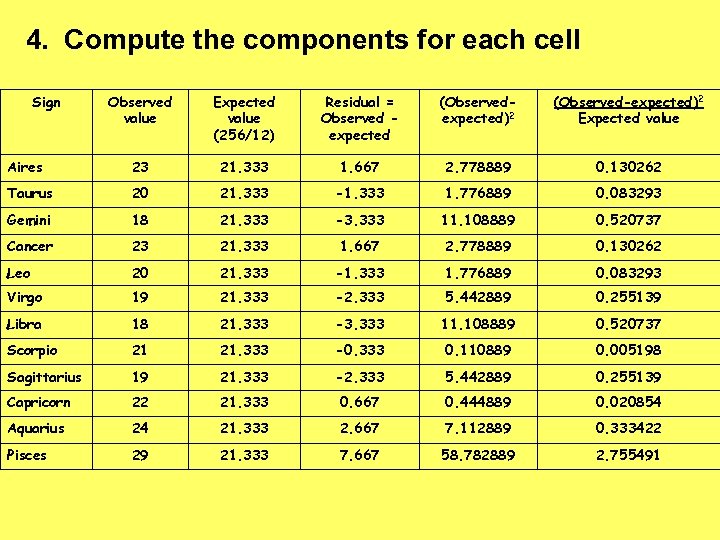4. Compute the components for each cell Sign Observed value Expected value (256/12) Residual = Observed expected (Observedexpected)2 (Observed-expected)2 Expected value Aires 23 21. 333 1. 667 2. 778889 0. 130262 Taurus 20 21. 333 -1. 333 1. 776889 0. 083293 Gemini 18 21. 333 -3. 333 11. 108889 0. 520737 Cancer 23 21. 333 1. 667 2. 778889 0. 130262 Leo 20 21. 333 -1. 333 1. 776889 0. 083293 Virgo 19 21. 333 -2. 333 5. 442889 0. 255139 Libra 18 21. 333 -3. 333 11. 108889 0. 520737 Scorpio 21 21. 333 -0. 333 0. 110889 0. 005198 Sagittarius 19 21. 333 -2. 333 5. 442889 0. 255139 Capricorn 22 21. 333 0. 667 0. 444889 0. 020854 Aquarius 24 21. 333 2. 667 7. 112889 0. 333422 Pisces 29 21. 333 7. 667 58. 782889 2. 755491

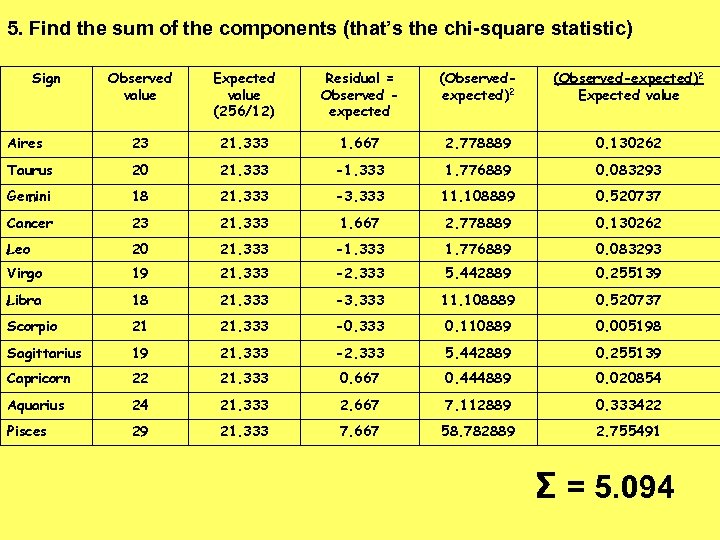5. Find the sum of the components (that’s the chi-square statistic) Sign Observed value Expected value (256/12) Residual = Observed expected (Observedexpected)2 (Observed-expected)2 Expected value Aires 23 21. 333 1. 667 2. 778889 0. 130262 Taurus 20 21. 333 -1. 333 1. 776889 0. 083293 Gemini 18 21. 333 -3. 333 11. 108889 0. 520737 Cancer 23 21. 333 1. 667 2. 778889 0. 130262 Leo 20 21. 333 -1. 333 1. 776889 0. 083293 Virgo 19 21. 333 -2. 333 5. 442889 0. 255139 Libra 18 21. 333 -3. 333 11. 108889 0. 520737 Scorpio 21 21. 333 -0. 333 0. 110889 0. 005198 Sagittarius 19 21. 333 -2. 333 5. 442889 0. 255139 Capricorn 22 21. 333 0. 667 0. 444889 0. 020854 Aquarius 24 21. 333 2. 667 7. 112889 0. 333422 Pisces 29 21. 333 7. 667 58. 782889 2. 755491 Σ = 5. 094

P-value = c 2 cdf(5. 094, 10^99, 11) =. 9265 a =. 05 Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that the CEOs are born under some signs more than under others.

Offspring of certain there are 4 categories, Since fruit flies may have yellow or ebony bodies and normal wings or df = 4 1 = 3 short wings. Genetic theory –predicts that Expected appear these traits willcounts: in the ratio 9: 3: 3: 1 Y & N = 56. 25 (yellow & normal, yellow & short, ebony & Y & S = 18. 75 normal, ebony & short) A researcher checks E & N = 18. 75 100 such E & S and finds the distribution 100 flies = 6. 25 expect 9/16 of the of We traits to be 59, 20, 11, and 10, respectively. flies to have yellow and normal wings. df? What are the expected counts? (Y & N) Are the results consistent with theoretical distribution predicted by the genetic model? (see next page)

Assumptions: • Have a random sample of fruit flies • All expected counts are greater than 5. Expected counts: Y & N = 56. 25, Y & S = 18. 75, E & N = 18. 75, E & S = 6. 25 H 0: The proportions of fruit flies are the same as theoretical model. Ha: At least one of the proportions of fruit flies is not the same as theoretical model. P-value = c 2 cdf(5. 671, 10^99, 3) =. 129 a =. 05 Since p-value > a, I fail to reject H 0. There is not sufficient evidence to suggest that the distribution of fruit flies is not the same as theoretical model.

A company says its premium mixture of nuts contains 10% Brazil nuts, 20% cashews, 20% almonds, 10% hazelnuts and 40% peanuts. You buy a large can and separate the nuts. Upon weighing them, you find there are 112 g Brazil nuts, 183 g of cashews, 207 g of almonds, 71 g or hazelnuts, and 446 g of peanuts. You Because we do NOT wonder whether your mix ishave counts of the significantly different from what the company advertises? type of nuts. Why NOT We could count the number is the chi-square goodness-of-fit test of each type of nut and appropriate here? then perform a c 2 test. What might you do instead of weighing the nuts in order to use chi-square?

Example: Does the color of a car influence the chance that it will be stolen? Of 830 cars reported stolen, 140 were white, 100 were blue, 270 were red, 230 were black, and 90 were other colors. It is known that 15% of all cars are white, 15% are blue, 35% are red, 30% are black, and 5% are other colors. Category Color Observed Expected 1 White 140 . 15*830 = 124. 5 2 Blue 100 . 15*830 = 124. 5 3 Red 270 . 35*830 = 290. 5 4 Black 230 . 30*830 = 249 5 Other 90 . 05*830 = 41. 5

Category Color Observed Expected 1 White 140 124. 5 2 Blue 100 124. 5 3 Red 270 290. 5 4 Black 230 249 5 Other 90 41. 5 Let π1, π2, . . . Π 5 denote true proportions of stolen cars that fall into the 5 color categories Ho: π1 =. 15, π2 =. 15, π3 =. 35, π4 =. 30, π5 =. 05 Ha: Ho is not true. α =. 01 Test statistic: Assumptions: The sample was a random sample of stolen cars. All expected counts are greater than 5, so the sample size is large enough to use the chi-square test.

Calculations: = 1. 93 + 4. 82 + 1. 45 + 56. 68 = 66. 33 P-value: All expected counts exceed 5, so the P-value can be based on a chi-square distribution with 4 df. The computed value is larger than 18. 46, so P-value <. 001. Because P-value < α, Ho is rejected. There is convincing evidence that at least one of the color proportions for stolen cars differs from the corresponding proportion for all cars.