Четные и нечетные функции Периодичность функций Демонстрационный материал

Скачать презентацию Четные и нечетные функции Периодичность функций Демонстрационный материал

Чётные и нечётные функции. Периодичность функций. Демонстрационный материал.ppt

Количество слайдов: 9

Четные и нечетные функции. Периодичность функций Демонстрационный материал 10 класс

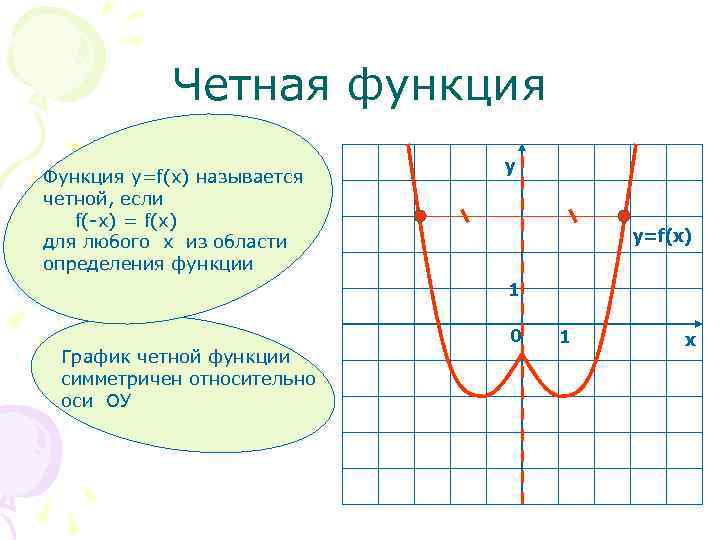Четная функция Функция у=f(x) называется четной, если f(-x) = f(x) для любого х из области определения функции у y=f(x) 1 График четной функции симметричен относительно оси ОУ 0 1 х

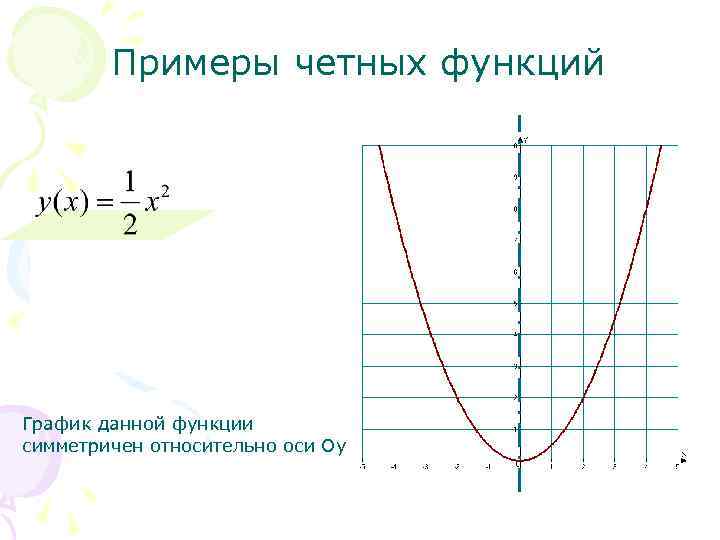Примеры четных функций График данной функции симметричен относительно оси Оу

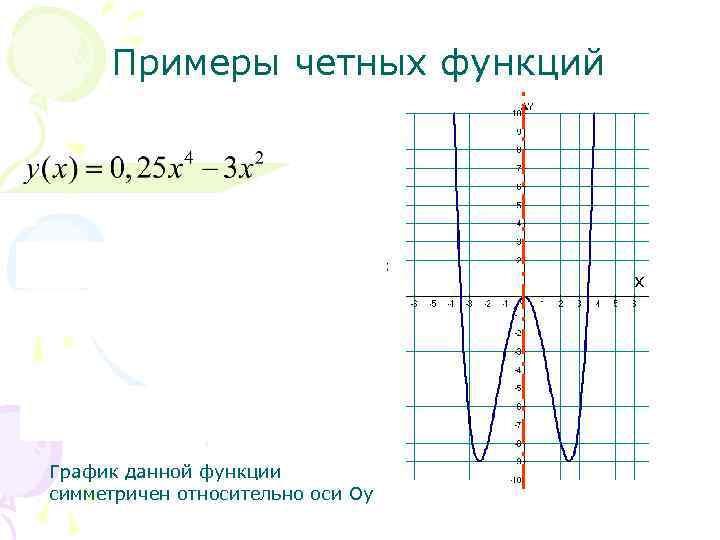Примеры четных функций х График данной функции симметричен относительно оси Оу

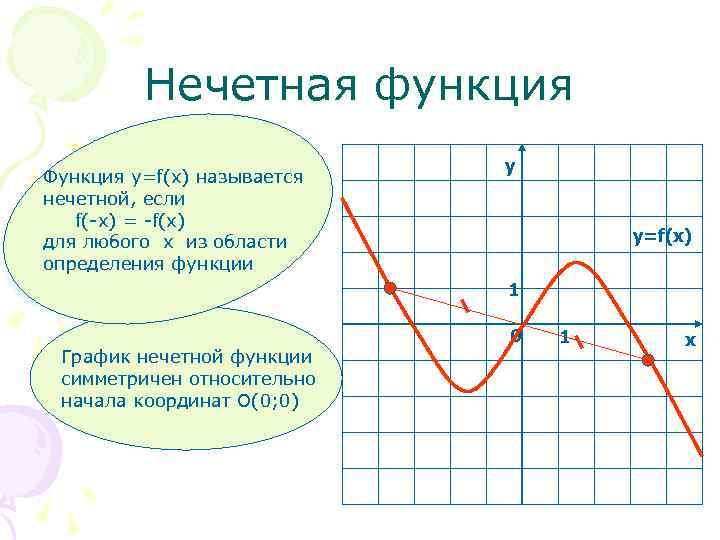Нечетная функция Функция у=f(x) называется нечетной, если f(-x) = -f(x) для любого х из области определения функции у y=f(x) 1 График нечетной функции симметричен относительно начала координат О(0; 0) 0 1 х

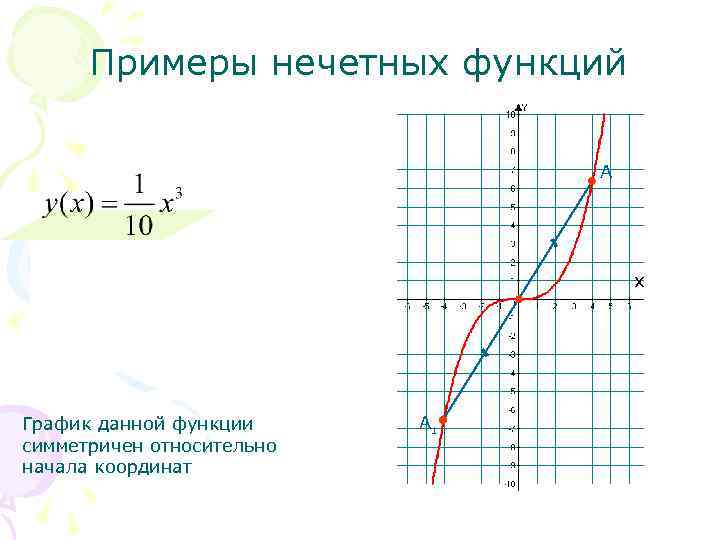Примеры нечетных функций А х График данной функции симметричен относительно начала координат А 1

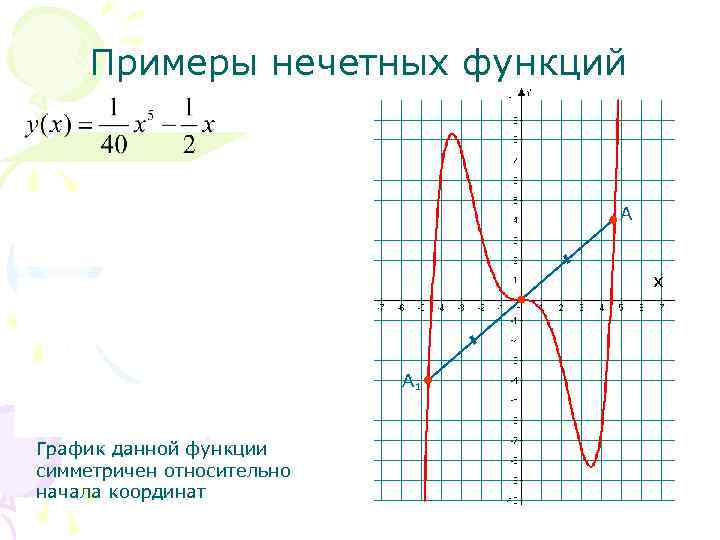Примеры нечетных функций А х А 1 График данной функции симметричен относительно начала координат

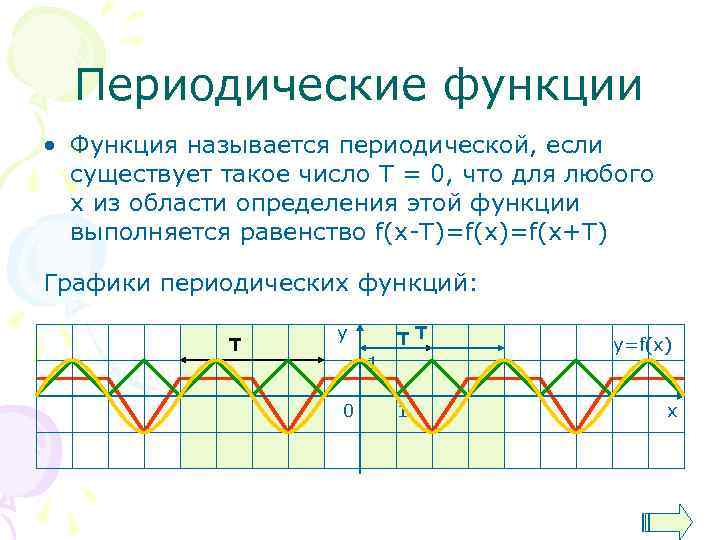Периодические функции • Функция называется периодической, если существует такое число Т = 0, что для любого х из области определения этой функции выполняется равенство f(x-T)=f(x+T) Графики периодических функций: Т у TT 1 0 1 y=f(x) х