Чернюк З. В. ЗОШ№ 22, м. Рівне.
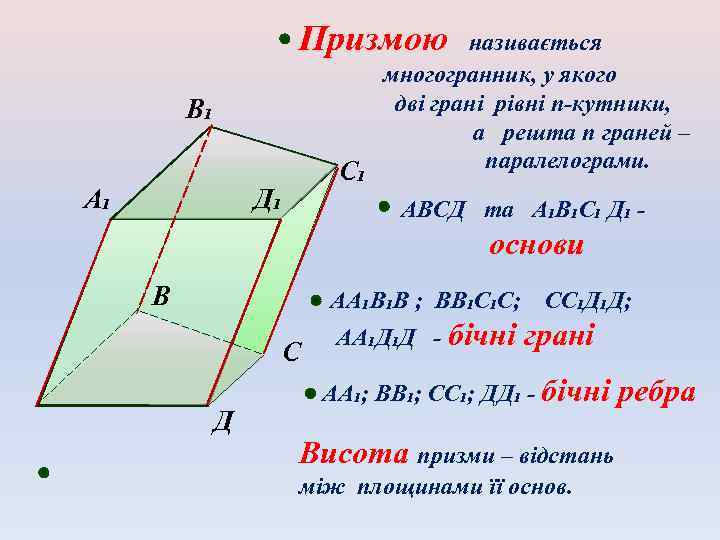Призмою називається многогранник, у якого дві грані рівні п-кутники, а решта п граней – паралелограми. С₁ В₁ А₁ Д₁ АВСД та А₁В₁С₁ Д₁ - основи В АА₁В₁В ; ВВ₁С₁С; С Д АА₁Д₁Д - бічні СС₁Д₁Д; грані АА₁; ВВ₁; СС₁; ДД₁ - бічні Висота призми – відстань між площинами її основ. ребра
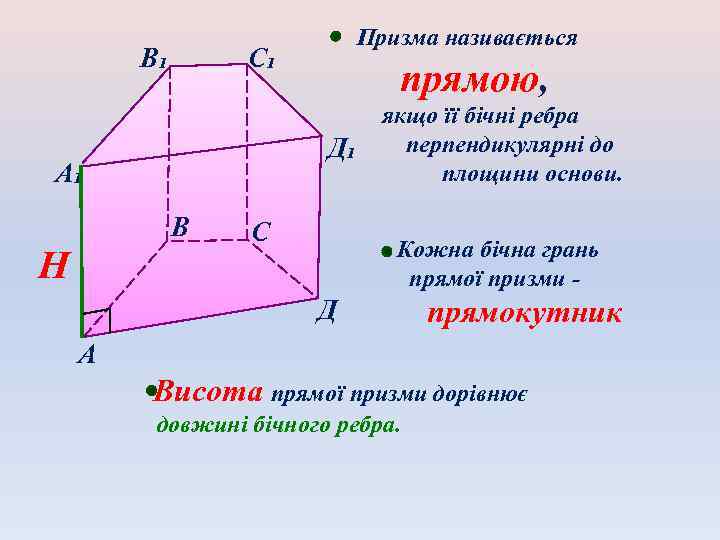В₁ С₁ прямою, Д₁ А₁ В Н Призма називається С якщо її бічні ребра перпендикулярні до площини основи. Кожна бічна грань прямої призми - Д прямокутник А Висота прямої призми дорівнює довжині бічного ребра.
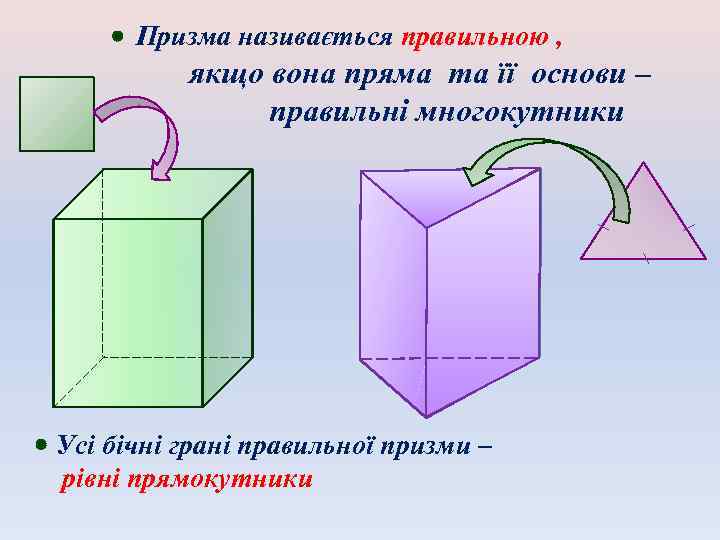Призма називається правильною , якщо вона пряма та її основи – правильні многокутники Усі бічні грані правильної призми – рівні прямокутники
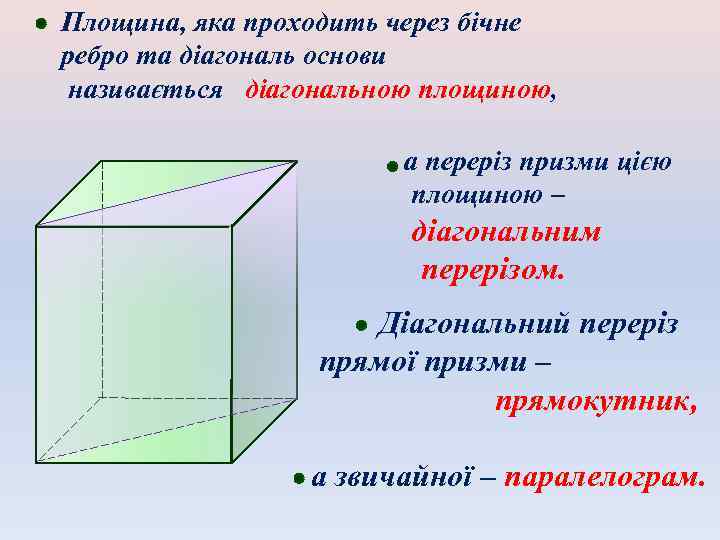Площина, яка проходить через бічне ребро та діагональ основи називається діагональною площиною, а переріз призми цією площиною – діагональним перерізом. Діагональний переріз прямої призми – прямокутник, а звичайної – паралелограм.
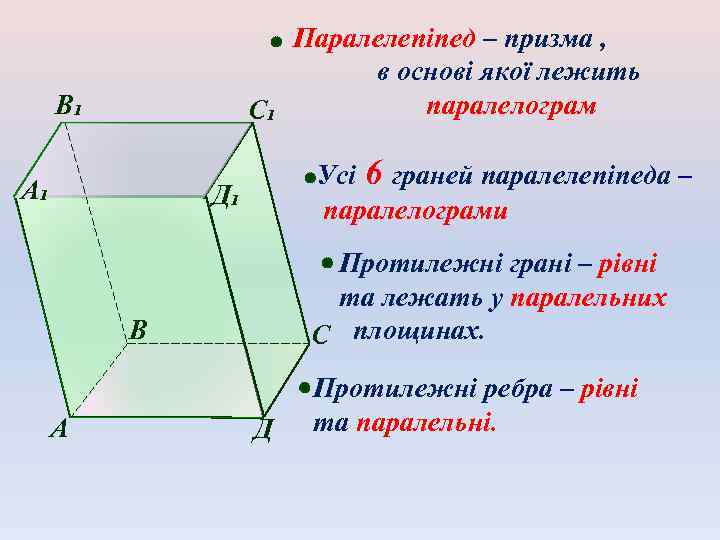Паралелепіпед – призма , в основі якої лежить паралелограм С₁ В₁ А₁ Усі 6 граней паралелепіпеда – паралелограми Д₁ Протилежні грані – рівні та лежать у паралельних С площинах. В А Д Протилежні ребра – рівні та паралельні.
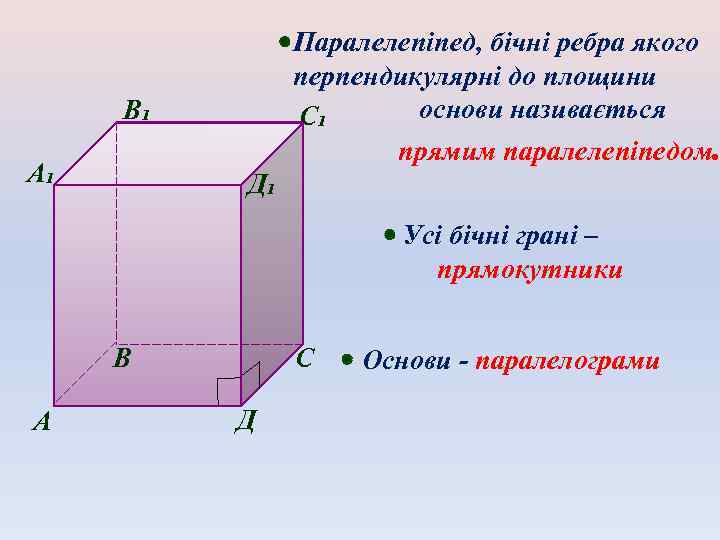Паралелепіпед, бічні ребра якого перпендикулярні до площини основи називається С₁ прямим паралелепіпедом. В₁ А₁ Д₁ Усі бічні грані – прямокутники В А С Д Основи - паралелограми
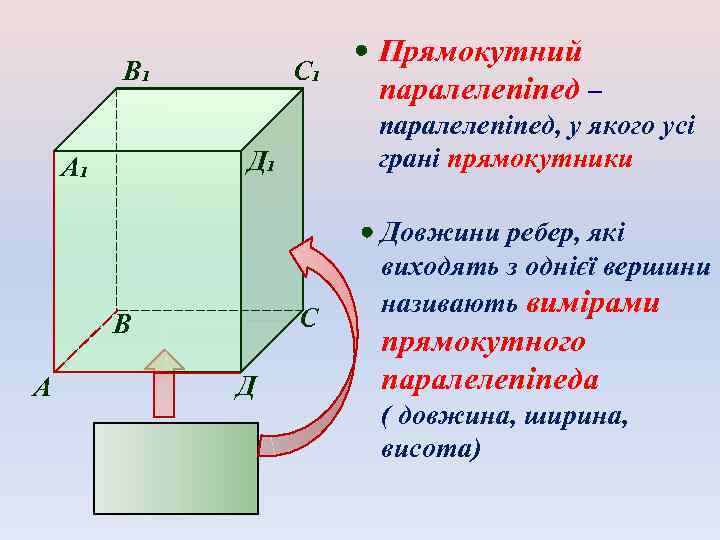В₁ С₁ С В А паралелепіпед, у якого усі грані прямокутники Д₁ А₁ Д Прямокутний паралелепіпед – Довжини ребер, які виходять з однієї вершини називають вимірами прямокутного паралелепіпеда ( довжина, ширина, висота)
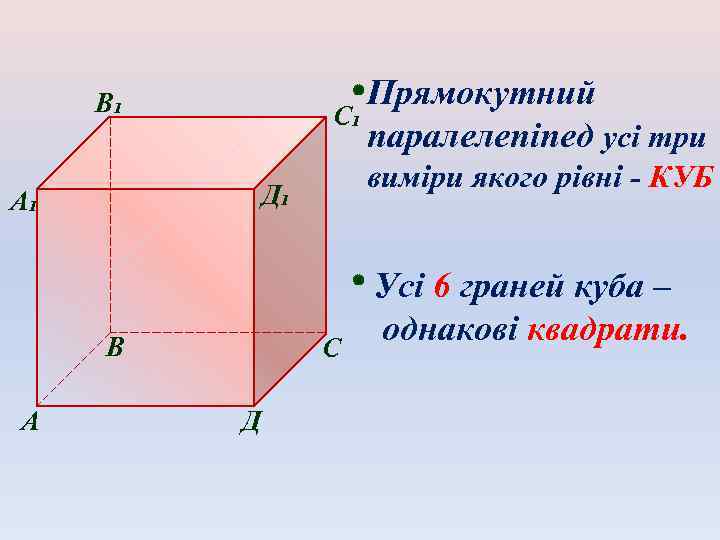Прямокутний С₁ паралелепіпед усі три В₁ Д₁ А₁ В А виміри якого рівні - КУБ С Д Усі 6 граней куба – однакові квадрати.
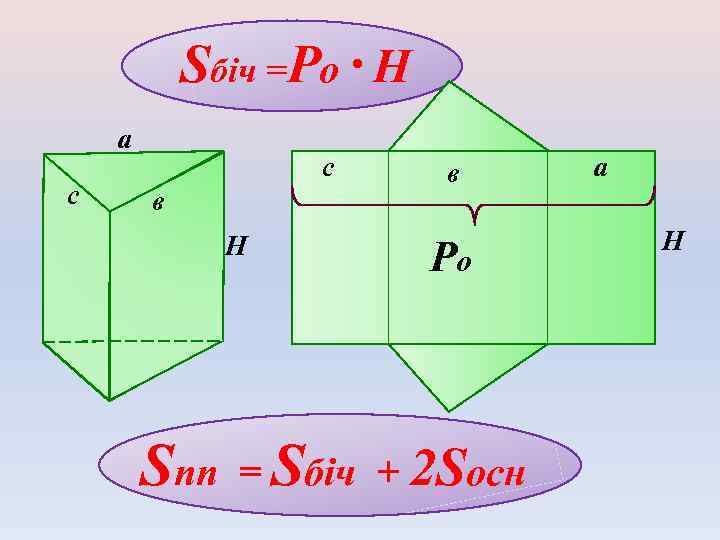Sбіч =Pо · H а с с в H в Pо Sпп = Sбіч + 2 Sосн а H
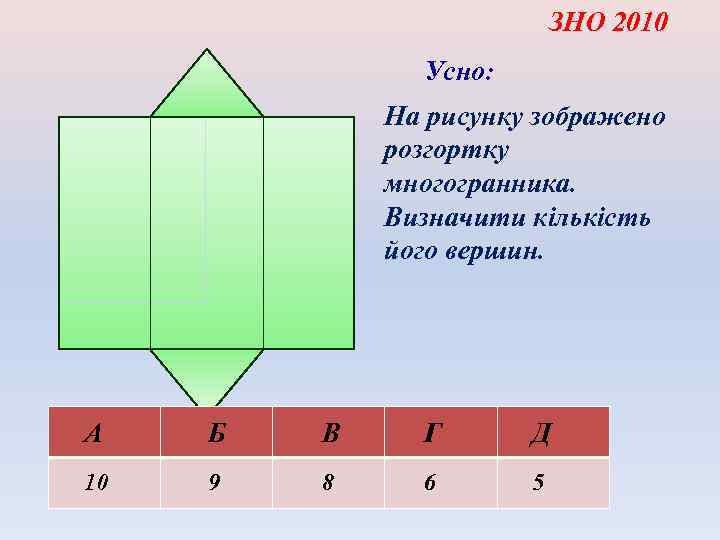ЗНО 2010 Усно: На рисунку зображено розгортку многогранника. Визначити кількість його вершин. А Б В Г Д 10 9 8 6 5
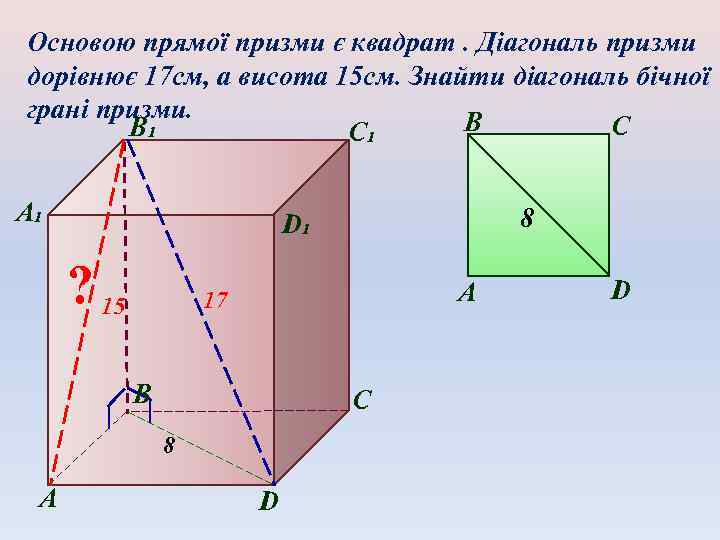Основою прямої призми є квадрат. Діагональ призми дорівнює 17 см, а висота 15 см. Знайти діагональ бічної грані призми. B C В₁ С₁ А₁ ? 15 А 17 В С 8 А 8 D₁ D D
Знайти ребро куба , якщо площа його діагонального перерізу 16√ 2 см². В₁ А₁ ? А С₁ А₁ Д₁ 16 S= м² 2 с √ В D 16 √ 2 см² х С C₁ А х√ 2 С
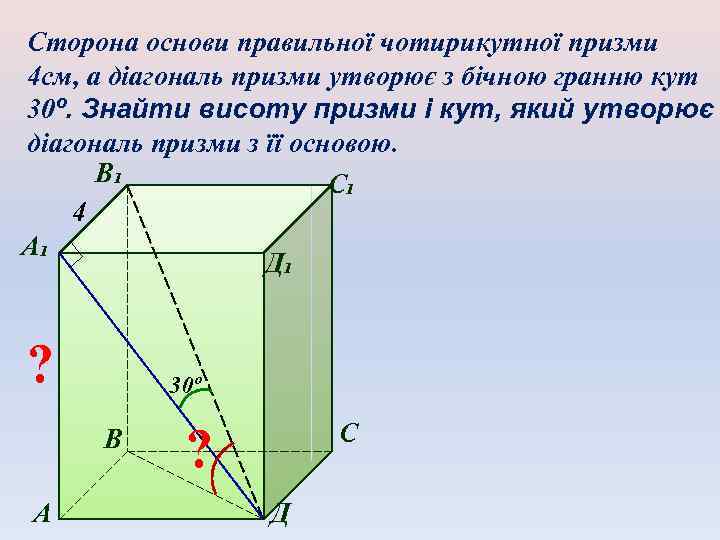Сторона основи правильної чотирикутної призми 4 см, а діагональ призми утворює з бічною гранню кут 30º. Знайти висоту призми і кут, який утворює діагональ призми з її основою. В₁ С₁ 4 А₁ Д₁ ? 30º В А С ? Д
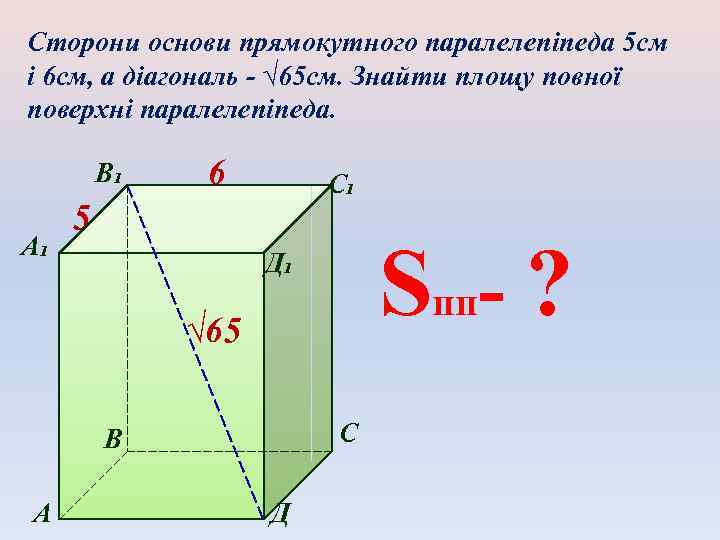Сторони основи прямокутного паралелепіпеда 5 см і 6 см, а діагональ - √ 65 см. Знайти площу повної поверхні паралелепіпеда. В₁ А₁ 6 С₁ 5 Sпп- ? Д₁ √ 65 С В А Д
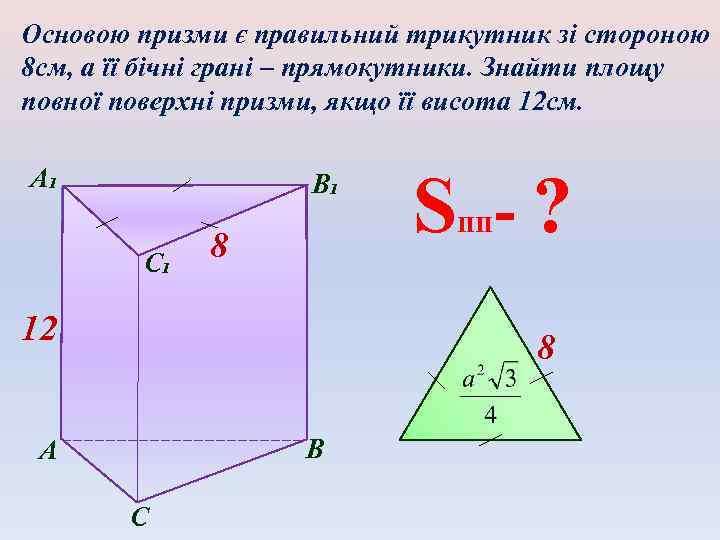Основою призми є правильний трикутник зі стороною 8 см, а її бічні грані – прямокутники. Знайти площу повної поверхні призми, якщо її висота 12 см. А₁ В₁ С₁ S -? пп 8 12 8 В А С
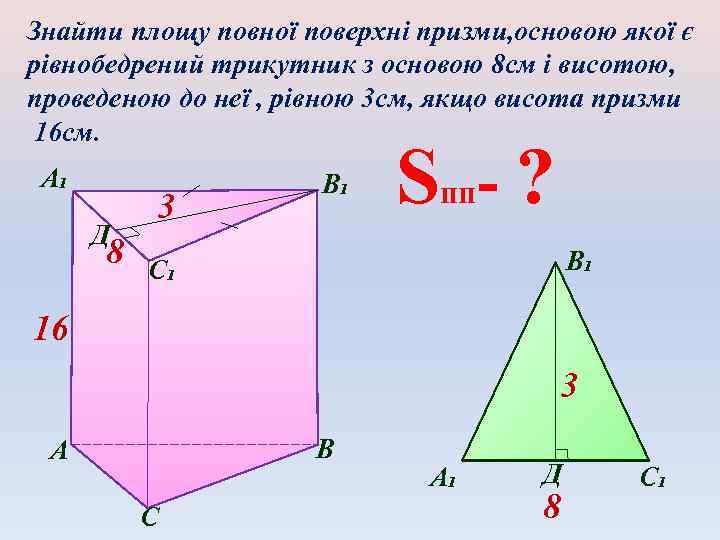Знайти площу повної поверхні призми, основою якої є рівнобедрений трикутник з основою 8 см і висотою, проведеною до неї , рівною 3 см, якщо висота призми 16 см. А₁ Д 8 3 В₁ S -? пп В₁ С₁ 16 3 В А С А₁ Д 8 С₁
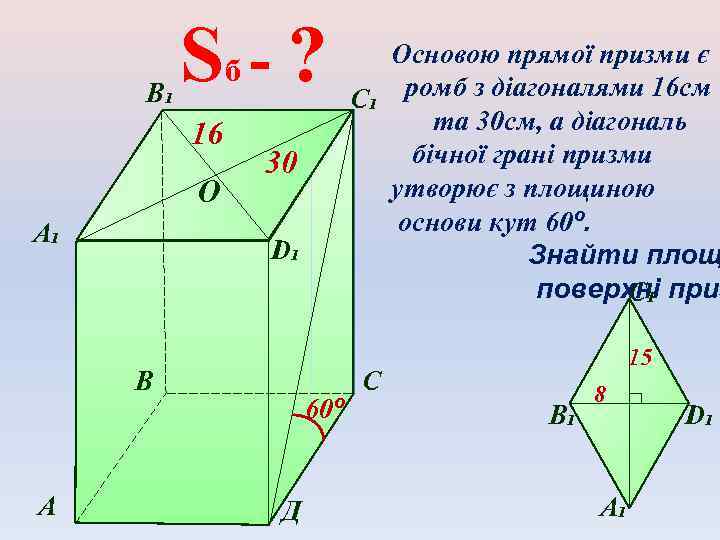В₁ S -? б 16 О А₁ 30 D₁ В А 60º Д Основою прямої призми є С₁ ромб з діагоналями 16 см та 30 см, а діагональ бічної грані призми утворює з площиною основи кут 60º. Знайти площ поверхні приз С₁ 15 С В₁ 8 А₁ D₁
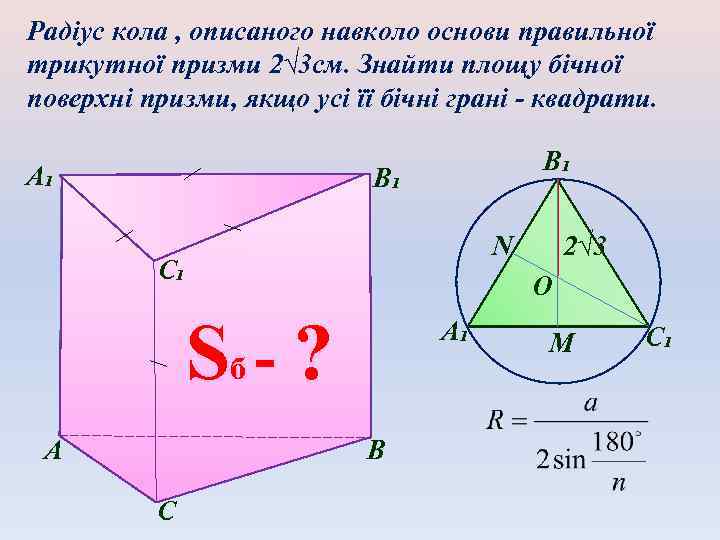Радіус кола , описаного навколо основи правильної трикутної призми 2√ 3 см. Знайти площу бічної поверхні призми, якщо усі її бічні грані - квадрати. А₁ В₁ В₁ N С₁ O S -? А₁ б А В С 2√ 3 M С₁
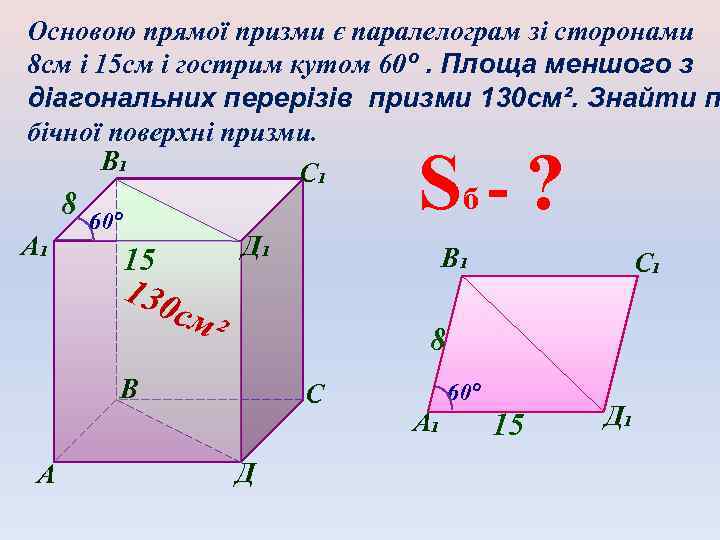Основою прямої призми є паралелограм зі сторонами 8 см і 15 см і гострим кутом 60º. Площа меншого з діагональних перерізів призми 130 см². Знайти п бічної поверхні призми. В₁ С₁ 8 А₁ S -? б 60º Д₁ 15 В₁ 130 см² 8 В А С₁ С Д 60º А₁ 15 Д₁
Сторони основ прямої трикутної призми 10 см, 17 см, 21 см, а площа повної поверхні призми 312 см². Знайти довжину її бічного ребра. 17 А₁ 10 С₁ ? Sпп В₁ 21 С 17 21 = 312 см² В А 10
Основою прямої призми є рівнобічна трапеція , менша основа якої 8 см, а гострий кут – 60º. Діагоналі трапеції є бісектрисами її гострих кутів. Знайт Sбп, якщо діагональ призми утворює з площиною основи кут 30º. В₁ С₁ 8 б S -? А₁ 60º Д₁ В С 30º А Д