Чернышев Георгий Линейные списки Список Динамическая структура

Чернышев Георгий Линейные списки

Список Динамическая структура данных Позволяет неограниченный рост размера Требует специальных механизмов обращения Состоит из Указателя на первый элемент Каждый элемент указывает на следующий и хранит данные Последний элемент указывает на NIL

Динамические структуры данных Указатель Адрес в куче Позволяет использовать более 64 KByte сегмента: ▪ VAR Buffer : ARRAY [1. . $FFF 0] OF CHAR; Позволяет работать с динамическими типами данных Значение любого указателя – АДРЕС

Операции с указателями Объявление с помощью символа “^” Так: TYPE P 1 Ptr = ^INTEGER Или так: VAR P 1 : ^INTEGER Присваивание Другому указателю NIL Объекту по адресу (@), переменной например Запись по адресу простого типа: P 1^ : = 7; - после выделения Операции с памятью Выделение памяти NEW(P) Освобождение DISPOSE(P)

Примеры VAR P 1, P 2 : ^INTEGER; P 3: INTEGER BEGIN NEW(P 1); NEW(P 2); P 1^ : = 7; P 2^ : = 10; P 1^ : = P 2^*P 1^; P 3 : = 2; P 2 : = @P 3; END;

Сложности Необходимо следить за выделяемой памятью Не выделять повторно память выделенную с помощью NEW, без вызова DISPOSE Инициализировать указатели при объявлении В конце программы возвращать память ставшую ненужной DISPOSE только освобождает память, сам указатель надо вручную приравнивать к NIL Всегда иметь ссылку на выделенную память.

Объявление списка TYPE PELEM = ^ELEM; ELEM = record val: INTEGER; p. Next: PELEM; end;

Добавление элемента VAR p. Begin: ^ELEM; // исходный список cur: ^ELEM; // временный элемент BEGIN FOR i: = 1 TO 10 BEGIN NEW(cur); cur^. p. Next : = p. Begin; cur^. val : = i; p. Begin : = cur; END;

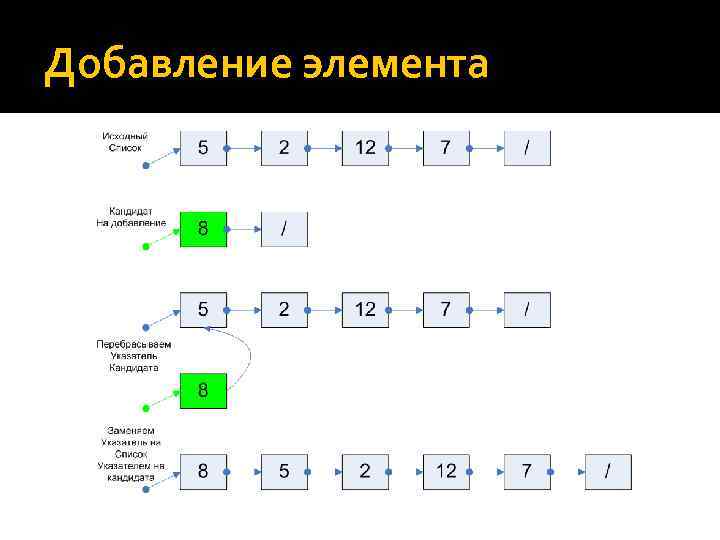Добавление элемента

Поиск элемента в списке VAR p. Begin: ^ELEM; // Список где ищем cur: ^ELEM; BEGIN cur : = p. Begin; while (cur <> NIL) DO BEGIN IF (cur^. val = 5) BEGIN WRITELN(“EXIST!”); BREAK; END; cur : = cur^. p. Next; END; IF (cur = NIL) WRITELN(“NOT EXIST!”); END;

Удаление элемента VAR p. Begin: ^ELEM; // основной список cur: ^ELEM; temp: ^ELEM; BEGIN cur : = find. Prev(p. Begin, 12); // функция возвращает указатель на предыдущий элемент с значением 12, в списке p. Begin if (cur = NIL) RETURN; temp : = cur^. next; cur^. next : = cur^. next; DISPOSE(temp); END; // Когда не будет работать? // Две причины

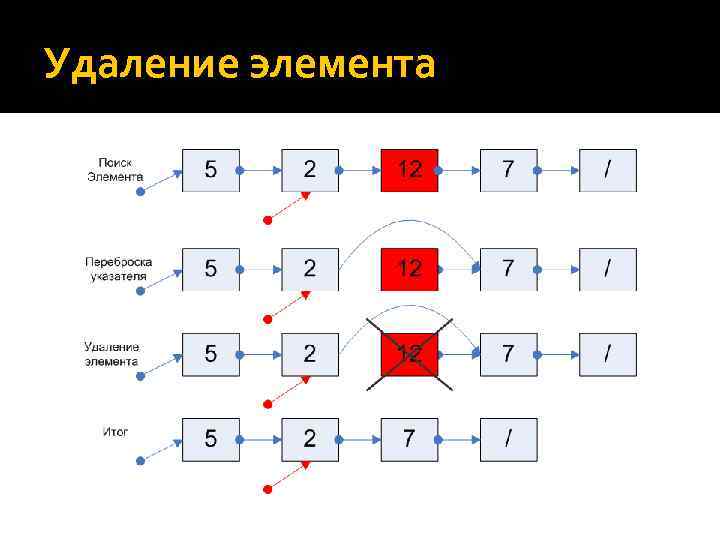Удаление элемента

В кратце (+) Добавление за O(1) Динамическая структура данных: не фиксирован размер, дешева вставка на любую позицию, удаление (-): Отсутствие произвольного доступа (плохо подходит для хранения упорядоченной информации) Дорогой поиск Динамическая структура данных: необходимо следить за выделенной памятью

Эффективность Добавление Удаление Поиск Линейный список O(1) Поиск+O(1) O(n) Сортированный Массив O(logn) + сдвиг O(1) + сдвиг O(logn) Бинарное дерево O(logn) Поиск+O(1) O(logn)

Задачи Для зачета за эту тему надо набрать 3 балла Задачи без * считаются за 1 балл Задачи со * и ** считаются соответственно за 2 и 3 балла Некоторые задачи имеют дополнения в условиях, при которых их ценность повышается. Для зачета этого типа задач необходимо предъявить оба варианта (и простой вариант тоже)

Задача – “Телефонная книга” Поддерживать упорядоченный список фамилий с телефонами Реализовать вставку, удаление, поиск, печать всего списка по порядку Все эти операции должны не нарушать свойство упорядоченности

Задача – “Реорганизация” Дан список списков групп, где каждый список группы содержит фамилию и балл за экзамен по предмету информатика Необходимо: создать 3 потока – сильный, слабый и очень слабый А) при этом потоки должны быть равны Б) могут быть не равны, но состав групп должен быть однороден

Задача – “Балансировщик” Даны P 1, P 2, … Pm – список игроков, каждый игрок имеет определенную силу, целое число N команд Составить (по возможности) равные команды, выведя их списки

Задача – “Map. Reduce” Дан список списков вещественных чисел Реализовать сортировку слиянием Нельзя пользоваться массивами Вернуть единый список Этот алгоритм применяется для распределенной сортировки больших массивов чисел

Задача – “Поворот” Дан список списков целочисленных элементов Необходимо его перевернуть При этом, повернуть каждый из списков Не использовать конвертацию в массивы

Задача – “Закупка” Даны Список магазинов S 1, S 2, S 3 … каждый из которых указывает на список товаров Список товаров магазина Si: Wi 1, Wi 2, Wi 3, … с ценами Ci 1, Ci 2, … Список товаров которые необходимо приобрести При этом, не все товары могут присутствовать с магазине, порядок магазинов, товаров произволен Найти минимальную стоимость покупки Вывести описывающий набор триплетов (Si, Wj, Сj) Сделать это оптимально за дополнительные баллы (* или даже **)

Задача – “Последовательность” Дан список с целочисленными элементами Найти возрастающую последовательность наибольшей длины

Задача – “Ошибка оператора” Дан линейный список (построить самому из массива) состоящий из элементов целочисленного типа В процессе построения, оператор, по ошибке, ввел некоторые элементы несколько раз Удалить все дубликаты, вернуть список Работая только со списками (конвертировать обратно в массив нельзя)

Задача – “Поиск” Дано два списка целых чисел: Данные D Запрос q Необходимо найти в данных все вхождения запроса: Числа из запроса идут непрерывно в D Числа из запроса могут прерываться Например при D = {1, 3, 6, 4, 6, 7} и q = {1, 3, 6} в первом случае будет найдено одно вхождение во втором - два

Задача – “Шпионы” Дано Список жителей P 1, P 2, …, Pn Список организаций O 1, O 2, …, Om. Каждый такой список содержит жителя, каждый из которых может состоять в нескольких организациях Известно что в город пробралось k шпионов Найти их, упорядочить по вероятности, если известно, что шпионы пытаются оставаться максимально незаметными и никуда не вступать

Задача – “Обмен” Даны два списка, и две пары чисел Вернуть два списка, у которых части ограниченные этими числами переставлены местами. Если таких чисел в каком-либо списке нет, то вернуть исходные

Задача – “Свертка списка” Вычислить левую свертку списка и вернуть список из одного элемента Свертка это f(…f(f(e 1, e 2, …, en 1), en 1+1, en 2+2, … e 2*n 11)…)

Задача – “Умное разделение” Дан список элементов l и два целых числа Mиn Вернуть M списков, где k-тый список вида ln*k, ln*k+1, …ln*(k+m)-1, ln*2 k+1

Задача – “Умножение матриц” Реализовать умножение матриц на списках Транспонирование, вычисление детерминанта по гауссу и вычисление следа даст *

Задача* – “Инквизиция” Дан список горожан p = {c 1, … , cm} и список еретиков l = {h 1, …, hn}. Каждый из них обладает какой-либо собственностью в городе, она задана с помощью списка (владение – список указателей на них). Собственность может находиться в коллективном владении. По закону, собственность нельзя реквизировать, если владеющие ей еретики в меньшинстве Найти всю собственность подлежащую конфискации

Задача* – “Транзакции” Транзакция R(Xi), W(Xi) – чтение и запись в переменную Xi C(i), A(i) – успешное и неуспешное завершение, конец транзакции Распутать список (в теории транзакций этот список называется расписание ) представляющий N транзакций (N - неизвестно), вернув список списков, каждый из которых содержит только операции из своей транзакции. Сделать это за 1 проход Нельзя конвертировать в массив Нельзя создавать элементы

Задача* – “Функциональная библиотека” Реализовать библиотеку со следующими функциями Обращение списка Фильтрация списка по условию на элемент Конкатенация списков Поиск в списке Для простоты можно считать что все элементы списка – целые числа

Задача* – “Функциональная библиотека-2” Объект список списков целых чисел Реализовать операции Поиск подсписка Удаление, Вставка Слияние, разбиение Клонирование

Задача* – “Функциональная библиотека-3” Объект – список целых чисел, реализовать Multisplit – вернуть список списков состоящих из исходных элементов разделенных указанным числом Замена по шаблону: q – исходное выражение вида li, li+1, li+2…, li+n -> lj, lj+1, … lj+m; lj in A. . Z Необходимо применить последовательно к линейному списку. Примеры: ▪ Список 1, 5, 7, 3, 14, 6, 2 ▪ Q: ABC ->CA, RESULT: 7, 5, 6, 14 ▪ Q: AB -> BA, RESULT: 5, 1, 3, 7, 6, 14, 2

Задача* – “Контейнер” Реализовать контейнер “Множество” на списках Проверка наличия элемента Пересечение Объединение Разность множеств Удовлетворяло основному свойству множества (не мультимножества)

Задача* – “Поисковая машина” Даны: Набор S = {d 1, d 2, …, dn} текстовых документов, состоящих из набора слов Набор слов, являющийся запросом q (считаем что между ними AND) Требуется вывести наиболее релевантные документы к данному запросу с использованием инвертированных списков Функция релевантности – общее количество слов из запроса встречающихся в документе. Дополнительные очки за придумывание и реализацию лучшей функции, с обоснованием. Инвертированные списки – структура данных в которой каждому слову из S сопоставлен набор документов где оно встречается (и возможно другая информация, такое как место в документе итд)

Задача* – “Классы” Существует набор объектов O 1, O 2, … Дан список классов, каждый класс задан списком объектов в него входящих Однако, выяснилось что если объект принадлежит двум классам, то эти два класса есть один Найти и вывести получившиеся таким образом классы (замыкание)

Задача* – “Саботаж” Дан список городов P 1, P 2, …, Pn Дан список железнодорожных маршрутов R 1, R 2, …, Rm. Каждый маршрут задан последовательностью населенных пунктов Ri 1, Ri 2, …, Ri(i_j) (маршруты произвольной длины) Необходимо: Выбрать минимальное количество городов для проведения саботажа, так чтобы разрушить все маршруты (маршрут считается разрушенным если нельзя проехать из Ri 1 в Rii для всех i). Если есть несколько вариантов – вывести любой Дополнительные баллы за ту же задачу, но при облегчении саботажа (известно население городов), проводить легче там, где больше народа

Задача* – “Распутывание” Даны N пар (вершина 1, вершина 2) Параметры – наборы стартовых и конечных вершин S и F “Развязать” данный граф, представив пользователю все возможные списки путей Усложнение(доп. баллы): в вершинах записаны операции (+, *, -, /) и число, применяемых к предыдущему результату. Есть так же аккумулятор (стартует с 0 из любого S). Найти путь дающий максимальное значение, циклов нет

Задача** – “Выборочный Саботаж” Тоже самое что в простом саботаже, но Мэры некоторых городов наши люди, их нельзя обижать Задача – сделать тоже самое, но оставить нетронутыми Nij “верных” городов для каждого региона i или сказать что это невозможно

Задача** – “Региональный Саботаж” Как и в Саботаже заданы города и дороги Известна принадлежность города к региону В регионе есть столицы (несколько штук) Разрушить связность между регионами Связь разрушена если из любой столицы одного региона нельзя попасть во все Данные и все остальное на списках

Задача** – “Шпионы-2” То же самое что в шпионах, но Есть список шпионских организаций, которыми можно пренебречь Известно что у шпиона мало друзей (меньше 3 х), чем меньше тем более вероятнее что он шпион Найти их, упорядочить по убыванию вероятности Аггрегирующая функция?

Задача** – “Вагоны” Дан закольцованный список, каждый элемент которого содержит Указатель на следующий элемент Указатель на предыдущий элемент “Лампочку” – булеву переменную, инициализированную произвольно, можно менять Ходя по списку определить его длину Нельзя выходить за пределы модели – конвертировать в массивы итд. Можно использовать константный объем памяти

Задача** – “Копирование” Дан список из элементов, каждый из которых Хранит некоторое целочисленное значение Имеет указатель на следующий элемент Имеет дополнительный указатель, указывающий на произвольный элемент списка Необходимо откопировать за O(n)