Черкаський державний технологічний університет Тема Метод найменших квадратів

Черкаський державний технологічний університет Тема: «Метод найменших квадратів наближення функцій» Дисципліна “Інформаційні технології аналізу систем” Лекція 12 -13 Викладач: Герасименко І. В. © проф. Триус Ю. В.

Питання: 1. 2. 3. 4. 5. 6. Постановка задачі наближення функцій. Геометричний смисл задачі наближення функцій за методом найменших квадратів (МНК). Лінійне і квадратичне наближення за МНК. Приклади наближення функцій за МНК. Функції нелінійної регресії. Засоби наближення функцій в системах комп’ютерної математики.

1. Постановка задачі наближеня функцій. Дуже часто, особливо при аналізі емпіричних даних виникає необхідність знайти в явному вигляді функціональну залежність між величинами x та y , що одержані в результаті вимірювань або спостережень. При аналітичному дослідженні взаємозв’язку між двома величинами x та y здійснюють ряд спостережень і в результаті одержується таблиця значень:

1. Постановка задачі наближення функцій.

1. Постановка задачі наближення функцій.

1. Постановка задачі наближення функцій.

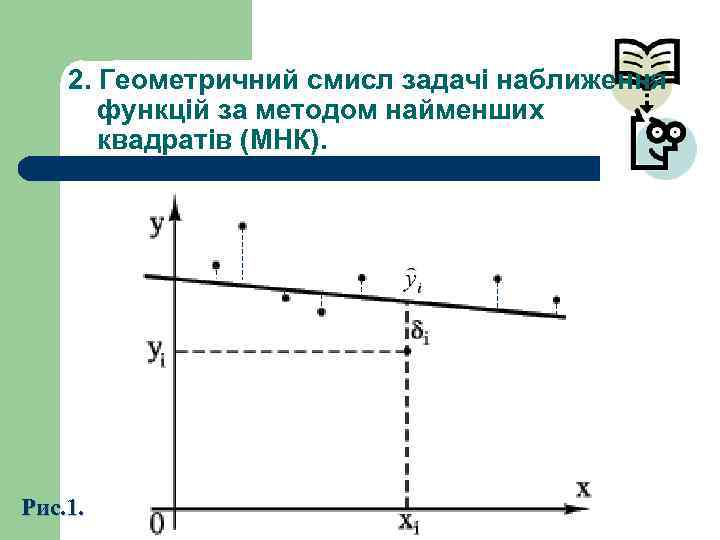2. Геометричний смисл задачі наближення функцій за методом найменших квадратів (МНК). Рис. 1.

3. Лінійне і квадратичне наближення за МНК 3. 1. Лінійне наближення Розглянемо наближення функції за допомогою лінійної функції за МНК. Тоді за формулою (2) треба розв’язати задачу мінімізації виду: Скориставшись для визначення невідомих коефіцієнтів a, b необхідними умовами екстремуму для функції від 2 -х змінних, отримуємо таку систему лінійних рівнянь:

3. Лінійне і квадратичне наближення за МНК 3. 1. Лінійне наближення (3) (4) Розв’язавши цю систему відносно a і b, одержимо явний вигляд лінійної функції наближення:

Приклад лінійного наближення Приклад 1. Нехай дослідним шляхом знайдено таблицю значень певної залежності. За допомогою МНК знайти лінійну функцію, яка якнайкраще наближає шукану залежність. x 1 2 3 4 5 6 y 5, 2 6, 3 7, 1 8, 5 9, 2 10, 0

Приклад лінійного наближення Розв’язування. Для розв’язування скористаємося одержаними раніше формулами: (4) (3) Для зручності занесемо результати проміжних обрахунків у таблицю: x y 1 2 3 4 5 6 5, 2 6, 3 7, 1 8, 5 9, 2 10, 0 21 46, 3 179, 1 91

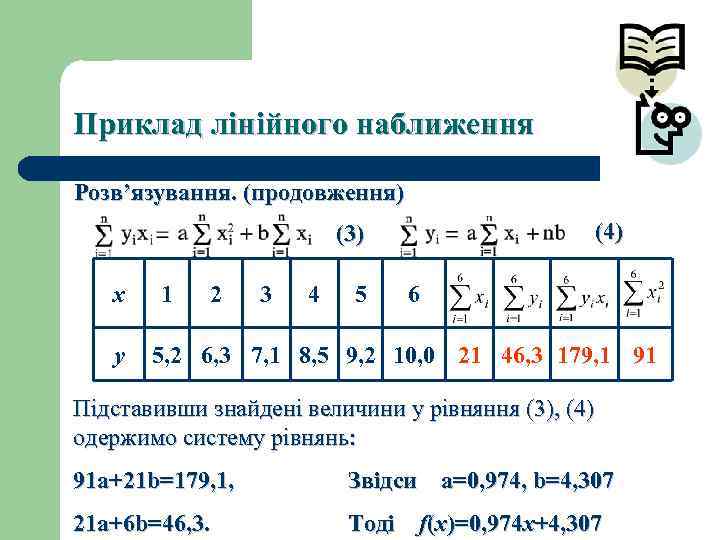Приклад лінійного наближення Розв’язування. (продовження) (4) (3) x y 1 2 3 4 5 6 5, 2 6, 3 7, 1 8, 5 9, 2 10, 0 21 46, 3 179, 1 91 Підставивши знайдені величини у рівняння (3), (4) одержимо систему рівнянь: 91 a+21 b=179, 1, Звідси a=0, 974, b=4, 307 21 a+6 b=46, 3. Тоді f(x)=0, 974 x+4, 307

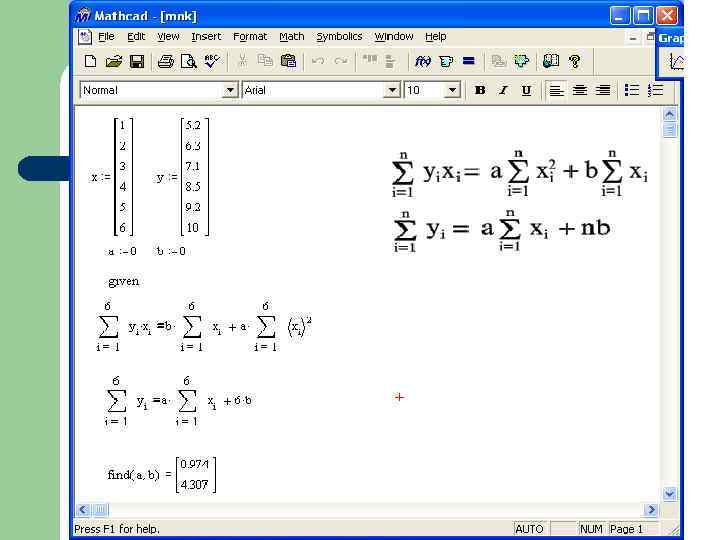
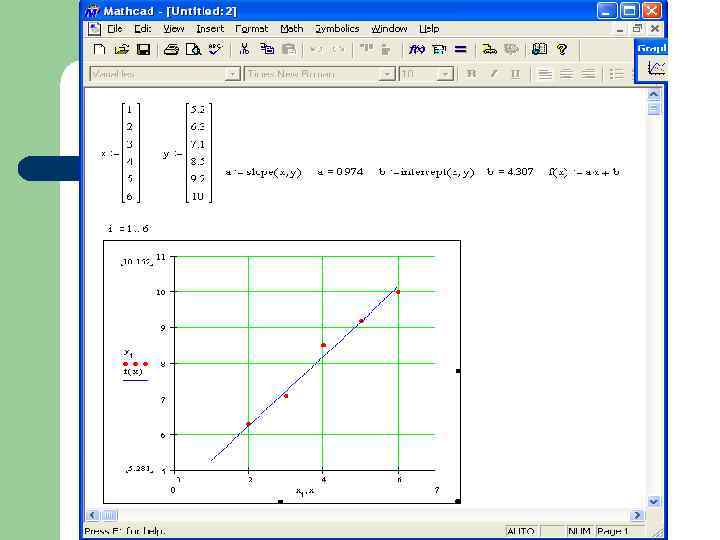
3. Лінійне і квадратичне наближення за МНК 3. 2. Квадратичне наближення Розглянемо наближення функції за допомогою квадратного тричлена за МНК. Тоді за формулою (2) треба розв’язати задачу мінімізації виду: (5) Скориставшись для визначення невідомих коефіцієнтів a, b, c необхідними умовами екстремуму для функції від 3 -х змінних, отримуємо таку систему лінійних рівнянь:

3. Лінійне і квадратичне наближення за МНК 3. 2. Квадратичне наближення (6) (7) (8)

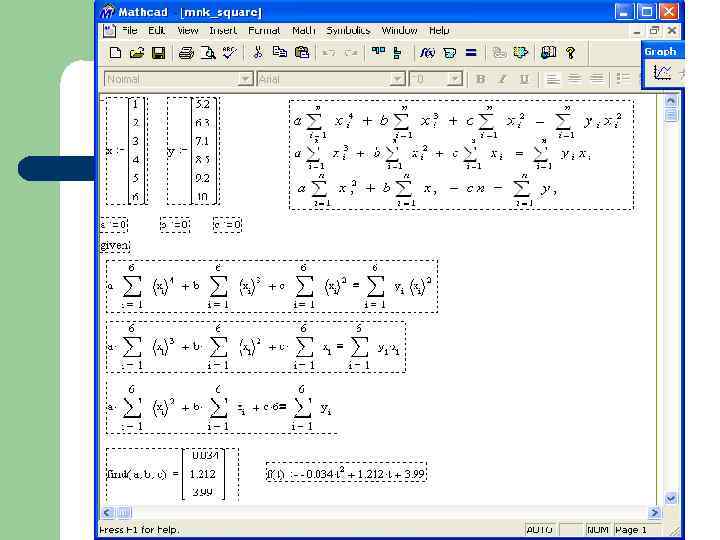
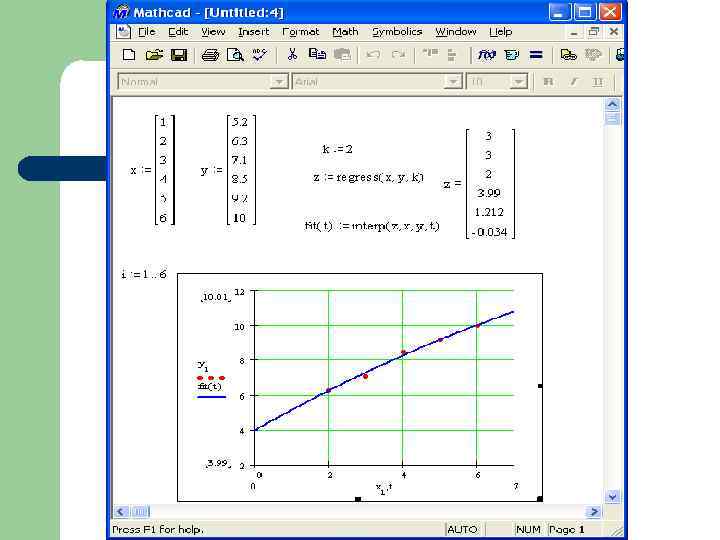
3. Лінійне і квадратичне наближення за МНК 3. 3. Поліноміальне наближення Розглянемо наближення функції за допомогою поліному m-го степеня за МНК.

5. Функції нелінійної регресії Враховуючи специфіку одержаної в результаті спостережень або вимірювань залежності, в якості апроксимуючої функції обирати різні функції, зокрема:

Ваші запитання 8(0472) 730271 herasymenkoinna@gmail. com Дякую за увагу!