Chemistry Atomic structure Session Objectives

Chemistry

Atomic structure

Session Objectives

Session objectives Schrodinger wave equation Shapes of orbitals Nodal Plane Quantum Numbers Rules for electronic configuration of an atom

Schrodinger wave equation Describes the probability of finding an electron in a given volume element.

Quantum mechanical model of atom The energy of electrons in atoms is quantised. The number of possible energy levels for electrons in atoms of different elements is a direct consequence of wave-like properties of electrons. The position and momentum of an electron cannot be determined simultaneously. Electrons of different energies are likely to be found in different regions. The region in which an electron with a specific energy will most probably be located is called an atomic orbital

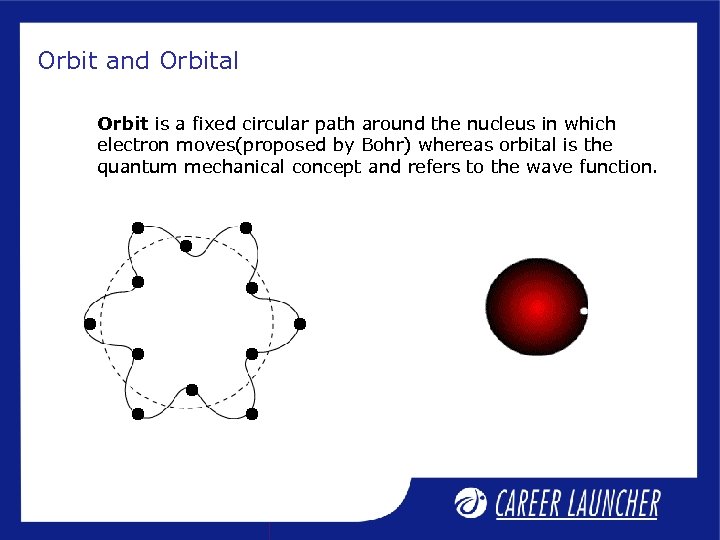
Orbit and Orbital Orbit is a fixed circular path around the nucleus in which electron moves(proposed by Bohr) whereas orbital is the quantum mechanical concept and refers to the wave function.

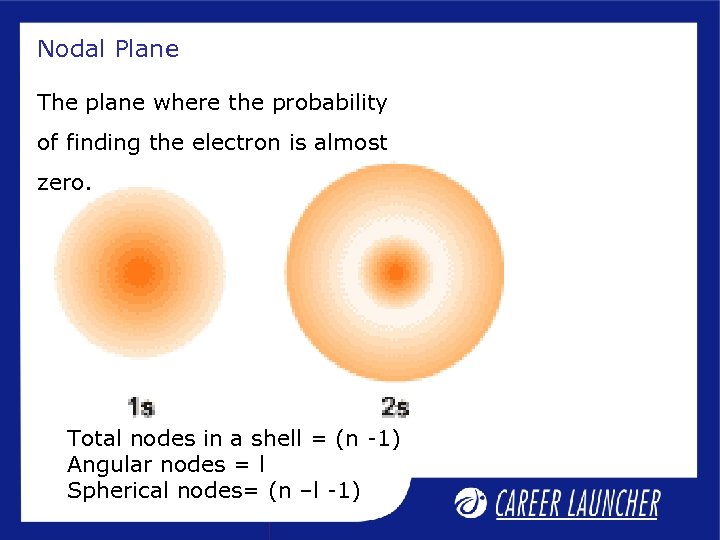
Nodal Plane The plane where the probability of finding the electron is almost zero. Total nodes in a shell = (n -1) Angular nodes = l Spherical nodes= (n –l -1)

Quantum Numbers They specify the address of each electron in an atom. These are four types. Quantum Numbers Azimuthal Principal Magnetic Spin

Principal Quantum Number (n) • Average distance of the electron from the nucleus • Energy Level of electron • Possible values (n=1, 2, 3…. . ) • Maximum number of electrons in any shell is 2 n 2. For example: In 3 d orbital, principal quantum number n is 3.

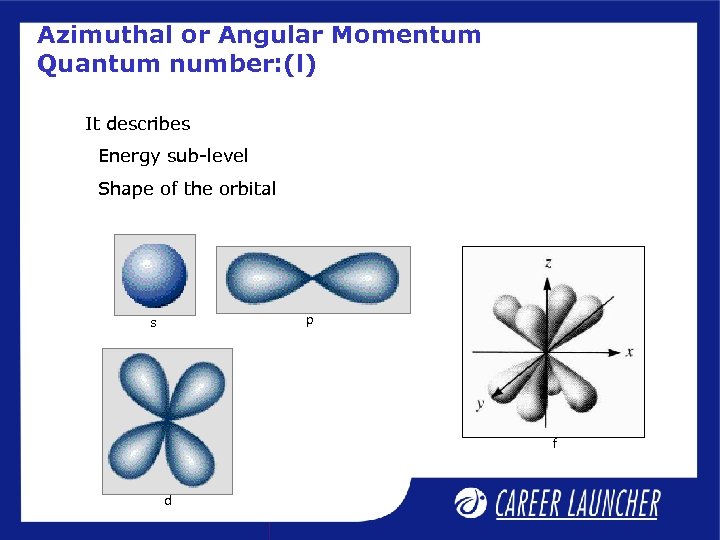
Azimuthal or Angular Momentum Quantum number: (l) It describes Energy sub-level Shape of the orbital p s f d

Quantum Numbers Orbital angular momentum of an electron is given by s p d f Values of l 0 1 2 3 Subshell

Illustrative example The orbital angular momentum of an electron is 4 s orbital is (b) zero AIEEE 2003 Solution Orbital angular momentum = For s electrons, l = 0 For 4 s electrons, orbital angular momentum is zero. Hence, answer is (b)

Magnetic quantum number(m) Magnetic Quantum Number (ml) Orientations of an orbital in space. Explains the Stark and Zeeman effect. Takes (2 l+1) values, m=- l to + l. Specifies Orbitals the exact orbital within each sublevel combine to form a spherical shape: 2 s 2 px 2 py 2 pz

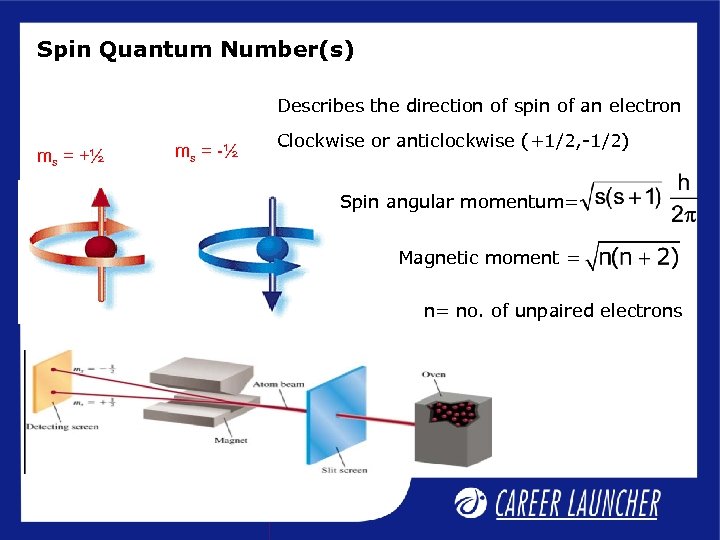
Spin Quantum Number(s) Describes the direction of spin of an electron ms = +½ ms = -½ Clockwise or anticlockwise (+1/2, -1/2) Spin angular momentum= Magnetic moment = n= no. of unpaired electrons

Relation between quantum numbers • For every value of n, l = 0 to (n-1) • For every value of l, m = -l to +l • For every value of m, s =

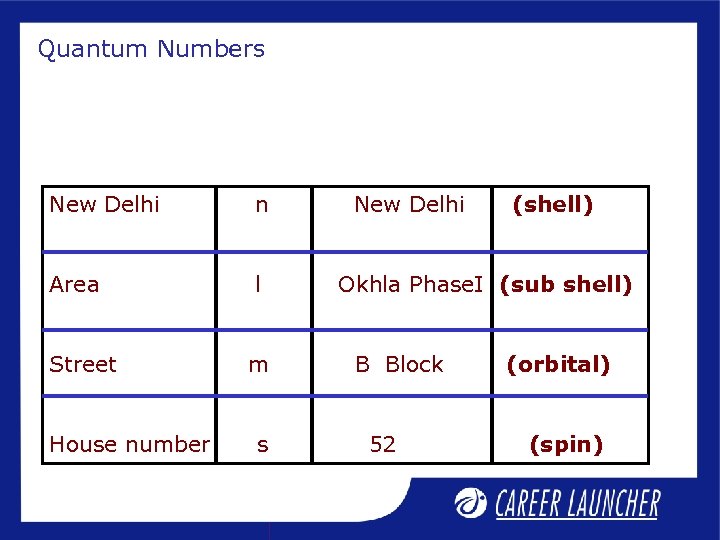
Quantum Numbers New Delhi n Area l Street m House number s New Delhi (shell) Okhla Phase. I (sub shell) B Block 52 (orbital) (spin)

Illustrative example Write down all the four quantum numbers for the last electron of oxygen. Solution: Oxygen (Z=8) having configuration i. e. , 16 = 1 s 2 2 p 4 8 O hence, for the last electron n=2, l=1, m=-1, s=-1/2

Illustrative example The electrons, identified by quantum numbers n and l (i) n = 4, l = 1, (ii) n = 4, l = 0, (iii) n = 3, l = 2, (iv) n = 3, l = 1 can be placed in order of increasing energy from the lowest to the highest as (a) (iv) < (iii) < (i) (c) (i) < (ii) < (iv) (b) (ii) < (iv) < (iii) (d) (iii) < (iv) < (ii) Solution (i)n = 4, l = 1(4 p) (ii)n = 4, l = 0(4 s) (iii)n = 3, l = 2(3 d) (iv)n = 3, l = 1(3 p) According to Aufbau’s rule order of increasing energy of subshells is 3 p < 4 s < 3 d < 4 p or (iv) < (iii) < (i) Hence, answer is (a)

Illustrative Example A compound of vanadium has a magnetic moment of 1. 73 B. M. Find out the oxidation state of vanadium in the compound. Solution Magnetic moment = n=1 Electronic configuration of vanadium (23) is [Ar] 3 d 3 4 s 2 (five unpaired electrons) The compound contains only one unpaired electron, electronic configuration of V will be [Ar] 3 d 1 4 s 0 V is present as V 4+-

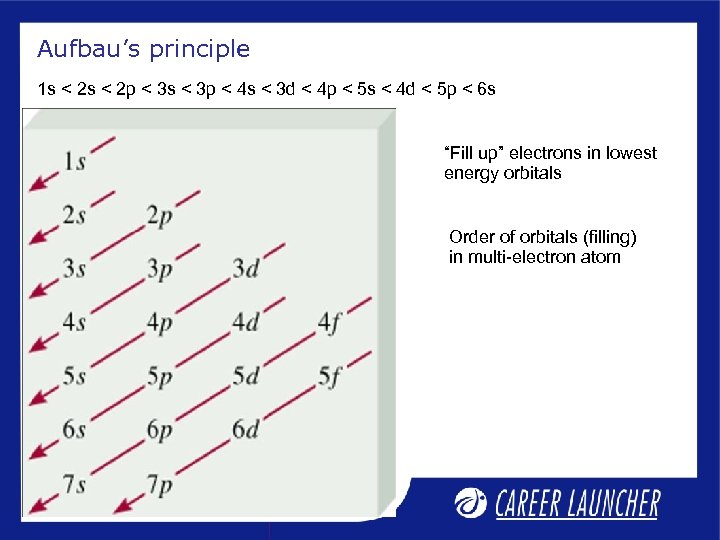
Aufbau’s principle 1 s < 2 p < 3 s < 3 p < 4 s < 3 d < 4 p < 5 s < 4 d < 5 p < 6 s “Fill up” electrons in lowest energy orbitals Order of orbitals (filling) in multi-electron atom

Aufbau’s principle For example: Consider 3 d and 4 s orbitals, the electron will first enter the orbital having minimum value of (n+l). Electron will therefore enter 4 s orbital (4+0=4) before entering 3 d orbital (3+2=5).

Aufbau’s principle Incase (n+l) values are same!!! Incase of 3 d orbital (3+2=5) and 4 p orbital (4+1=5), the (n+l) values are same. In such a case, electron enters the orbital for which n is minimum. The electron will thus enter 3 d orbital before entering 4 p orbital.

Pauli’s exclusion principle It is impossible for two electrons in a given atom to have same set of four quantum numbers. For example: Incase of 1 s 2, there are two electrons in the 1 s orbital. The quantum numbers of the two electrons are: n=1 , l=0 , m=0 , s=+1/2 n=1 , l=0 , m=0 , s=-1/2

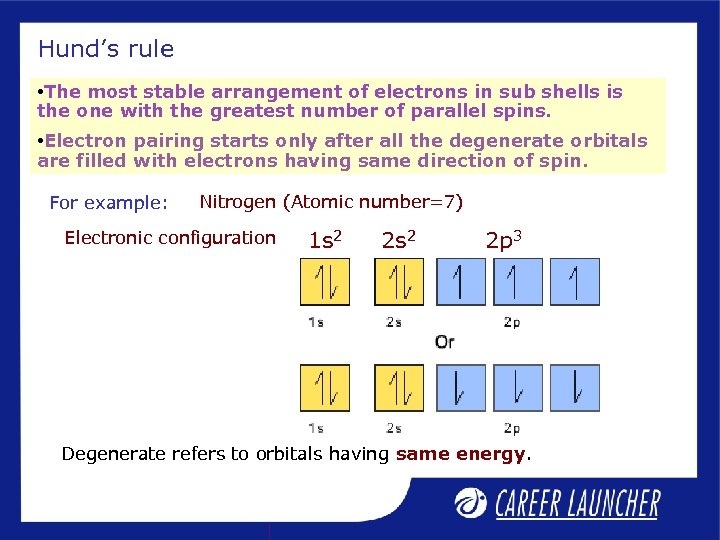
Hund’s rule • The most stable arrangement of electrons in sub shells is the one with the greatest number of parallel spins. • Electron pairing starts only after all the degenerate orbitals are filled with electrons having same direction of spin. For example: Nitrogen (Atomic number=7) Electronic configuration 1 s 2 2 p 3 Degenerate refers to orbitals having same energy.

Illustrative example If the nitrogen atom had electronic configuration 1 s 7, it would have energy lower than that of the normal ground state configuration 1 s 2 2 p 3, because the electrons would be closer to the nucleus. Yet 1 s 7 is not observed because it violates (a) Heisenberg’s uncertainty principle (c) Pauli exclusion principle (b) Hund’s rule (d) Bohr postulate of stationary orbits Solution According to Pauli’s exclusion principle, an orbital cannot have more than two electrons and these two with opposite spin. Hence, answer is (c)

Exceptional electronic configuration Orbitals in the same sub shell tend to become completely filled or half filled since such orbitals are more stable. Such as electronic configuration of Cr(24): [Ar]3 d 44 s 2 But actually it is [Ar]3 d 54 s 1

Illustrative example The electronic configuration of an element is 1 s 2 2 p 6 3 s 2 3 p 6 3 d 5 4 s 1. This represents its (a) excited state (b) ground state (c) cationic form (d) anionic form Solution The above electronic configuration is for ground state of chromium (3 d 5 4 s 1) Hence, answer is (b)

Class exercise

Class exercise-1 An electron is in one of 4 d orbitals. Which of the following quantum number is not possible? (a) n = 4 (b) l = 1 (c) m = 1 (d) m = 2 Solution b In 4 d orbital, n=4 l=2 m = – 2, – 1, 0, 1, 2 Therefore, the quantum number value which is not possible is (b). Hence correct option is (b)

Class exercise-2 An electron in an isolated atom may be described by four quantum numbers: n, l, m and s. The value of m for the most easily removed electron from a gaseous atom of an alkaline earth metal is (a) same as the maximum value of n for the element (b) any number from –(n – 1) to +(n – 1) (c) any positive number from 1 to ( n – 1) (d) zero Solution d Alkaline earth metal belongs to s block. The value of n for s block elements is 1. l = (n – 1) = 0 m=0 Hence correct option is (d)

Class exercise-3 The set of quantum numbers that represents the electron of highest energy is (a) n=1, l=0, m=0, s=+1/2 (b) n=2, l = 0, m=0, s=+1/2 (c) n=4, l=0, m=0, s=1/2 (d) n=3, l=2, m=0, s=+1/2 Solution d The set of quantum number which represents an electron of the highest energy has the maximum value of (n + l). Hence correct option is (d)

Class exercise-4 The number of electrons that can be accommodated by porbitals are (a) two electrons with parallel spins (b) six electrons (c) four electrons (d) eight electrons Solution b p orbital can accomodate a total of six electrons (two each in px, py, pz). Hence correct option is (b)

Class exercise-5 Which among the following set of quantum numbers is not possible? (a) n = 3, l = 0, m = 0 (b) n = 3, l = 1, m = 1 (c) n = 2, l = 1, m = 0 (d) n = 2, l = 0, m = – 1 Solution d The set of quantum number which is not possible is n = 2, l = 0, m = –. In this case, m = 0. Hence correct option is (d)

Class exercise-6 Which orbital has equal probability of finding an electron in all directions? Solution The s orbital has equal probability of finding an electron in all directions as it is spherical in shape, which is symmetrical around the nucleus.

Class exercise-7 What is the angular momentum of 4 s orbital? Solution Orbital angular momentum = In case of 4 s orbital, l=0 Orbital angular momentum is zero.

Class exercise-8 Why do some atoms exhibit exceptional electronic configuration? Solution Some atoms exhibit exceptional electronic configuration because half-filled orbitals and fully filled orbitals are more stable than partially filled orbitals.

Class exercise-9 Write down the electronic configuration for Si (atomic number 14), V (atomic number 23), Zn (atomic number 30), Kr (atomic number 36). Solution Si = 1 s 2 2 s 2 sp 6 3 s 2 3 p 2 V = 1 s 2 2 p 6 3 s 2 3 p 6 3 d 3 4 s 2 Zn = 1 s 2 2 p 6 3 s 2 3 p 6 3 d 10 4 s 2 Kr = 1 s 2 2 p 6 3 s 2 3 p 6 3 d 10 4 s 2 4 p 6

Class exercise-10 An electron is in a 4 d orbital. What possible values of the quantum numbers can it have? Solution n=4 l=2 m = ± 2, ± 1, 0 s=

Thank you