CHARMM GAMESS-UK Paul Sherwood CLRC Daresbury Laboratory p sherwood dl

CHARMM/GAMESS-UK Paul Sherwood CLRC Daresbury Laboratory p. sherwood@dl. ac. uk

Overview • Current implementation ¤ Parallel GAMESS-UK ¤ Results from Gaussian Blur / Double link atom tests ¤ Plans and suggestions for QM/MM in CHARMM • Link atom positions and forces • Boundary charge corrections • CHARMM performance on DL Beowulf clusters ¤ Pentium/Ethernet ¤ Alpha/Quadrics • Advert for QUASI workshop (Mülheim) Sept 25 -27 2000

CHARMM/GAMESS-UK Interface • Implemented with help from Bernie Brooks, Eric Billings • QM/MM model closely follows CHARMM/GAMESS(US) • Gaussian Blur implemented ¤ based on generic auxilliary charge density expansion - taken from Dunlap fitted DFT scheme. ¤ includes gradients ¤ could be generalised to coulomb interactions based on non-spherical charge densities ¤ Incorporated into parallel CHARMM, based on a single distributed QM calculation

GAMESS-UK Parallel Implementation ¤ Replicated data scheme • store P, F, S etc on every node • minimal communications (load balancing, global sum) • up to ca. 2000 basis functions ¤ Message-passing version (MPI, TCGMSG) • SCF and DFT • Suitable for < 32 processors ¤ Global Array version: • Parallel functionality – SCF, DFT, MP 2, SCF Hessian • Parallel algorithms – GAs for in-core storage of transformed integrals (to vvoo) and MP 2 amplitudes – parallel linear algebra (PEIGS, DIIS, MXM etc) – GA-mapped ATMOL file system

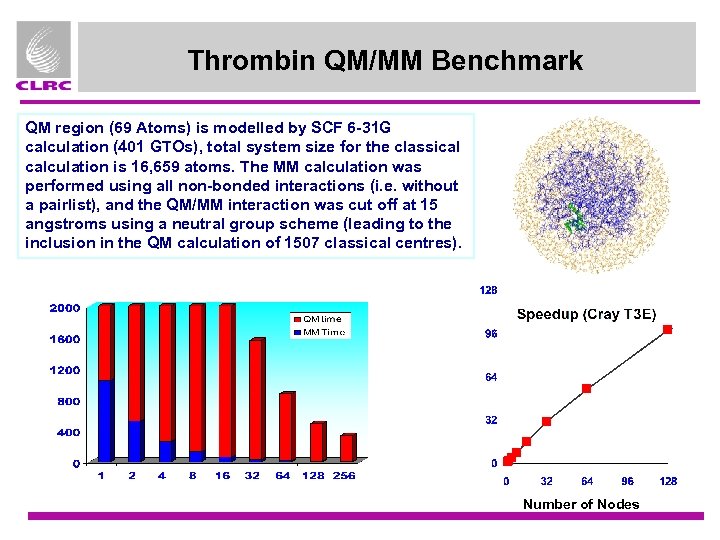
Thrombin QM/MM Benchmark QM region (69 Atoms) is modelled by SCF 6 -31 G calculation (401 GTOs), total system size for the classical calculation is 16, 659 atoms. The MM calculation was performed using all non-bonded interactions (i. e. without a pairlist), and the QM/MM interaction was cut off at 15 angstroms using a neutral group scheme (leading to the inclusion in the QM calculation of 1507 classical centres). Number of Nodes

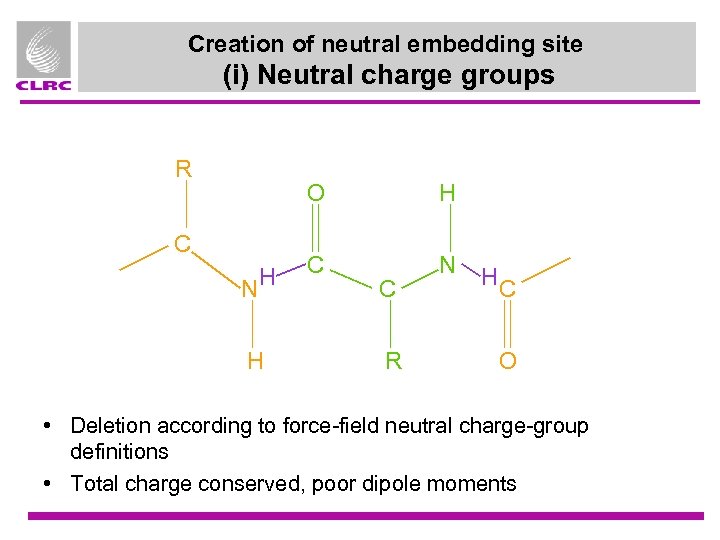
Creation of neutral embedding site (i) Neutral charge groups R O C NH H H C N C R HC O • Deletion according to force-field neutral charge-group definitions • Total charge conserved, poor dipole moments

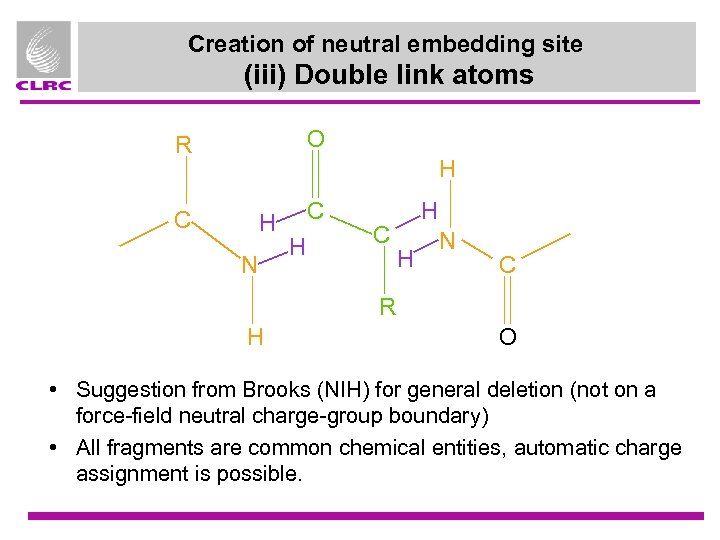
Creation of neutral embedding site (iii) Double link atoms O R H C H N C H H N C R H O • Suggestion from Brooks (NIH) for general deletion (not on a force-field neutral charge-group boundary) • All fragments are common chemical entities, automatic charge assignment is possible.

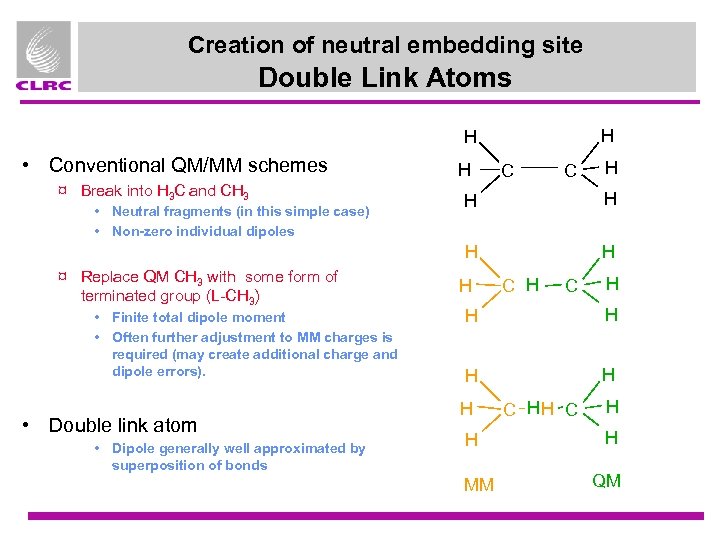
Creation of neutral embedding site Double Link Atoms H H • Conventional QM/MM schemes ¤ Break into H 3 C and CH 3 H C C H ¤ Replace QM CH 3 with some form of terminated group (L-CH 3) • Finite total dipole moment • Often further adjustment to MM charges is required (may create additional charge and dipole errors). • Double link atom • Dipole generally well approximated by superposition of bonds H H H • Neutral fragments (in this simple case) • Non-zero individual dipoles H H C H H H H MM C HH C H H QM

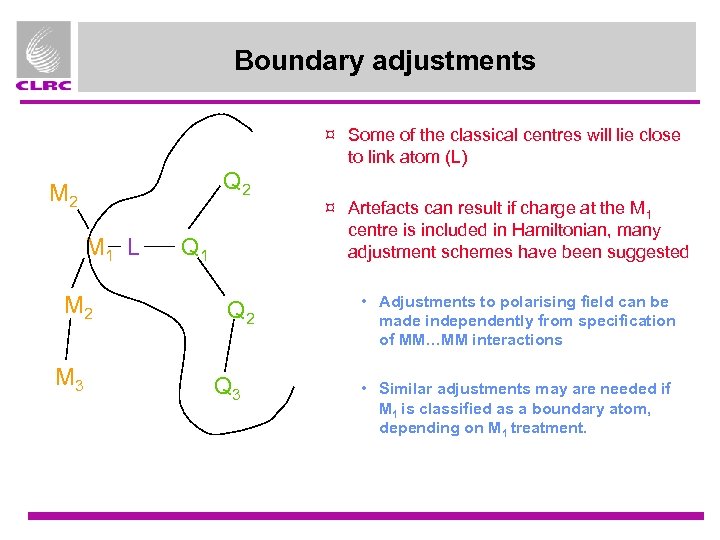
Boundary adjustments ¤ Some of the classical centres will lie close to link atom (L) Q 2 M 1 L M 2 M 3 Q 1 Q 2 Q 3 ¤ Artefacts can result if charge at the M 1 centre is included in Hamiltonian, many adjustment schemes have been suggested • Adjustments to polarising field can be made independently from specification of MM…MM interactions • Similar adjustments may are needed if M 1 is classified as a boundary atom, depending on M 1 treatment.

Boundary Adjustments (i) Selective deletion of 1 e integrals ¤ L 1: Delete integrals for which basis functions i or j are sited on the link atom L • found to be effective for semi-empirical wavefunctions • difference in potential acting on nearby basis functions causes unphysical polarisation for ab-initio QM models ¤ L 3: Delete integrals for which basis functions i and j are cited on the link atom and q. A is the neighbouring MM atom (M 1) • less consistent results observed in practice † † Classification from Antes and Thiel, in Combined Quantum Mechanical and Molecular Mechanical Methods, J. Gao and M. Thompson, eds. ACS Symp. Ser. , Washington DC, 1998.

Boundary Adjustments (ii) Deletion of first neutral charge group ¤ Thiel L 2, CHARMM EXGR Option ¤ Exclude charges on all atoms in the neutral group containing M 1 • Maintains correct MM charge – leading error is the missing dipole moment of the first charge group • Generally reliable – free from artefacts arising from close contacts • Limitations – only applicable in neutral group case (e. g. AMBER, CHARMM) – neutral groups are highly forcefield dependent • differ between MSI and Academic charmm – problematic if a charge group needs to be split • Application – biomolecular systems

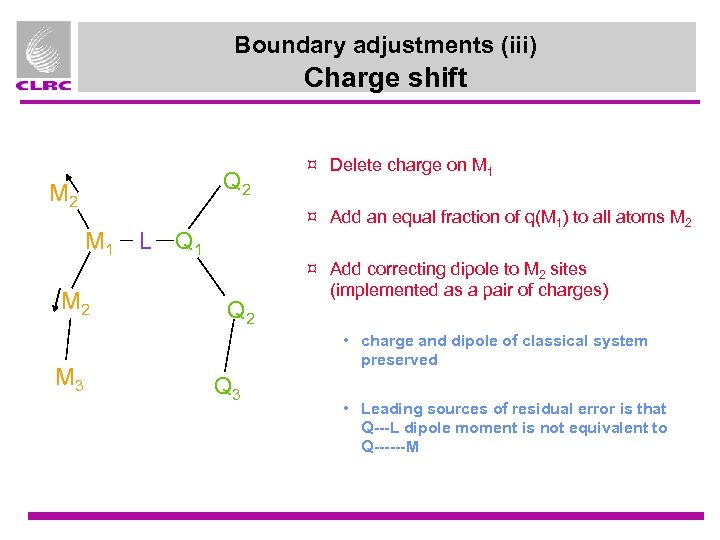
Boundary adjustments (iii) Charge shift Q 2 M 1 M 2 M 3 ¤ Delete charge on M 1 ¤ Add an equal fraction of q(M 1) to all atoms M 2 L Q 1 Q 2 ¤ Add correcting dipole to M 2 sites (implemented as a pair of charges) • charge and dipole of classical system preserved Q 3 • Leading sources of residual error is that Q---L dipole moment is not equivalent to Q------M

Boundary adjustments (iv) Gaussian Blur ¤ Delocalise point charge using Gaussian shape function • Large Gaussian width : electrostatic coupling disappears • Narrow Gaussian width : recover point charge behaviour • Intermediate values – short range interactions are attenuated – long range electrostatics are preserved ¤ Importance of balance - apply to entire MM system or to first neutral group ¤ Particularly valuable for double-link atom scheme where MM link atom charge lies within QM molecular envelope

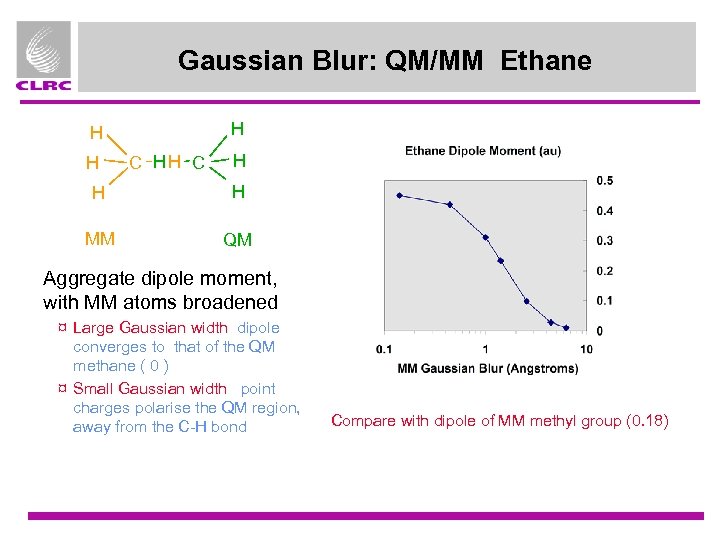
Gaussian Blur: QM/MM Ethane H H H C H H H MM QM Aggregate dipole moment, with MM atoms broadened ¤ Large Gaussian width dipole converges to that of the QM methane ( 0 ) ¤ Small Gaussian width point charges polarise the QM region, away from the C-H bond Compare with dipole of MM methyl group (0. 18)

QM/MM coupling - Proton Affinity Tests • Simplified alcohol test set based on [1] ¤ AMBER charge model ¤ QM region is small (HOCH 3 in all cases) ¤ Include systems with 1, 2 and 3 link atoms, Ethanol, i-Propanol, t-Butanol ¤ Fixed geometries (from 3 -21 G QM optimisations) ¤ Compare • Pure QM • L 2 (delete first charge group) • Shift (move charge from first atom to neighbours, add dipole. • Double link atom + Gaussian Blur CH 3 H O C H H CH 3 H O C CH 3 [1] I. Antes and W. Thiel, in “Hybrid Quantum Mechanical and Molecular Mechanical Methods” J. Gao (ed. ) ACS Symp. Ser. 712, ACS, Washington, DC, 1998.

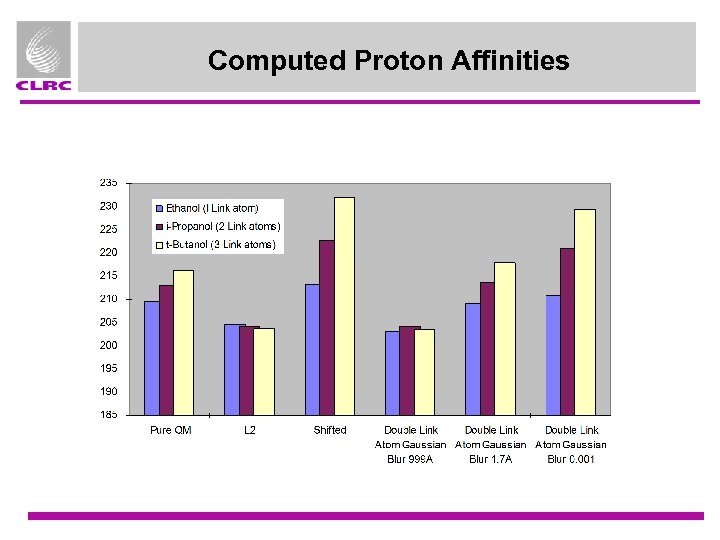
Computed Proton Affinities

Possible Developments • Planned in collaboration with NIH ¤ task-farmed parallel implementation (based on multiple MPI communicators) for use on high latency parallel machines (Beowulfs) ¤ Automated setup of double link atoms • Suggestions for QM/MM couplings ¤ Handling of link atoms - inclusion of chain run derivatives to remove link atoms from dynamics. ¤ Shifted charge at boundaries as an alternative to EXGR - especially where large neutral groups are involved.

Positioning of link atoms • Initial placement ¤ Usually on terminated bond • Unconstrained ¤ Additional degrees of freedom present in geometry optimisation and MD • e. g. CHARMM, QUEST • Constrained ¤ Need to take into account forces on link atoms, • shared internal coordinate definitions (IMOMM) • chain-rule differentiation (QM/Pot, Chem. Shell)

QUASI Workshop Modelling Catalysis - Quantum Simulations in Industry September 27 -27, MPI Mülheim • Plenary speakers ¤ ¤ M. Karplus (Strasbourg) - biocatalysis L. G. M Pettersson (Stockholm) - solid-state and surfaces J. Sauer (Berlin) - zeolites M. T. Reetz (MPI Mülheim) - experimental perspective • QUASI Consortium speakers ¤ C. R. A. Catlow, P. Sherwood, W. Thiel ¤ Industrial perspective • A. Schäfer (BASF), S. Rogers (ICI), M. Sjovoll (Hydro) ¤ M. F. Guest (HPC) • Posters and Hands-on session www. mpi-muelheim. de/QUASI/workshop

QUASI Workshop - Mülheim Sept 25 -27 2000 • Richard Catlow (Royal Institution, London) QM/MM Techniques for Modelling Bulk and Surface Properties of Oxide Materials · Joachim Sauer (Humboldt-Universität Berlin) QMPOT: A Powerful Tool for Modelling Catalysis by Zeolites • Martyn Guest (Daresbury Laboratory, CLRC) Molecular Modelling on High-End and Commodity-Type Computers: Status and Perspectives · Ansgar Schäfer (BASF, Ludwigshafen) Large-scale QM/MM Calculations on Enzymes · Helmut Schwarz (Technische Universität Berlin) Mechanistic Studies on the Platinum Mediated HCN Synthesis from Methane and Ammonia · Paul Sherwood (Daresbury Laboratory, CLRC) Implementation of the QM/MM Methodology within QUASI - a General Purpose Approach. · Merethe Sjovoll (Norsk Hydro, Porsgrunn) Catalytic Decomposition of Nitrogen Oxides by Transition Metal-Exchanged Zeolites · Walter Thiel (MPI für Kohlenforschung, Mülheim) QM/MM Studies on Enzymes: Methods and Applications · Martin Karplus (Université de Strasbourg) How Enzymes Work: Activation Energy and Dynamics · Lars Pettersson (University of Stockholm) To be announced · Manfred Reetz (MPI für Kohlenforschung, Mülheim) Evolution in the Test Tube as a Means to Create Enantioselective Enzymes for Organic Chemistry • Steve Rogers (ICI, Teesside) QM/MM Studies of Methanol Synthesis