Charge Diffusion and Resistive Films Method s Math s

Charge Diffusion, and Resistive Films Method’s , Math's, Monty Carlo’s, and Track reconstruction (with an M. . . ) By: Stephen Turnbull

An agenda § A quick look back, Why adding a resistive foil probably seamed like a good idea. § TPC evolution; benefits setbacks of old systems § Where Resistive foil stands § Physical object specifications (you be funny try it) § resistive film § mesh and pillars § And wide pads § Mathematical exploration § Pulse shape § Information retention § Simulate This! Carleton's TPC simulation § Capabilities § Data everywhere … now what to do with it all? § § § Current track reconstruction techniques Wonderful results Future plans

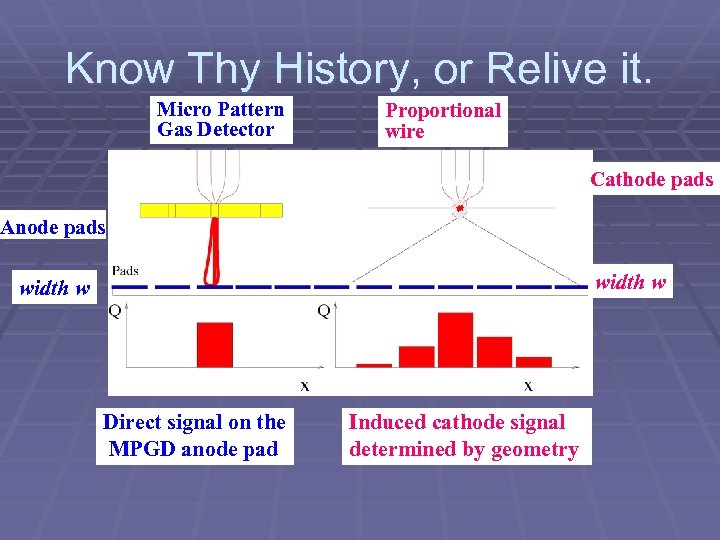Know Thy History, or Relive it. Micro Pattern Gas Detector Proportional wire Cathode pads Anode pads width w Direct signal on the MPGD anode pad Induced cathode signal determined by geometry

The Wire Chamber Strengths § It worked, this was a big one up on it’s predecessor which didn’t exist. § Capacitance To Anode Pads allowed space point determination. § Using centroid calculations of pad signals to ‘see’ event multiple times on relatively wide pads § Relative Pad Width independence Weaknesses § Ex. B § + ion back flow into gaseous volume § Relatively long recovery times / low rates § Preferential track directions

Standard Micro Pattern Gas Detector’s MPGD’s Strengths § Partial or near complete Positive Ion Capture § Negligible Ex. B effects § Track Angle Independence § Higher Rate Weaknesses § no/weak signal sharing between pads. § One or two pads contain all the signal, center of mass calculations difficult/impossible.

It would be ideal if only. . . A TPC could achieve very high gains With little or no spatial diffusion … But still register on 3 or more pads to allow center of mass calculations. Be track angle independent. All while not costing several fortunes (preferably) While we’re at it why not have it bring us coffee and the morning paper?

Resistive Films - Close enough? § These requests are easy enough, except for the being self contradictory part. § Low diffusion can be obtained by using very strong magnetic § § § fields. Small enough pads will promise signal distribution And (gain-wise) track angle independence is almost a give away with MPGD’s The only remaining problem is cost § Or, you can use a very thin highly resistive film overtop of your readout pads and win at all the races.

Resistive Foil and its prospects. § The Resistive foil readout method envisions even point § § like charges dissipating freely into a resistor capacitor network. The dissipating charge then can register on pads it passes over, yielding a centre of mass calculable event. The dispersion is geometric and electronic in nature, therefore arriving electron clusters can be kept as small as economically possible. Resistive foil methods can be coupled with standard MPGD amplification methods, with the added benefit that the resistive foil partially suppresses sparking. The amount and speed of charge decay can be customized by varying the glue or resistivity of the foil.

A TPC with resistive foil A quick look at the COSMo TPC, one realization of the vison.

The box, and Specifications • 15 cm drift length with GEM or Micromegas readout • Aleph charge preamps. Rise= 40 ns, Fall = 2 s. • Currently using 200 MHz FADCs but method remains effective at FADC speeds as low as 25 MHz. • 60 tracking pads (2 x 6 mm 2) + 2 trigger pads (24 x 6 mm 2).

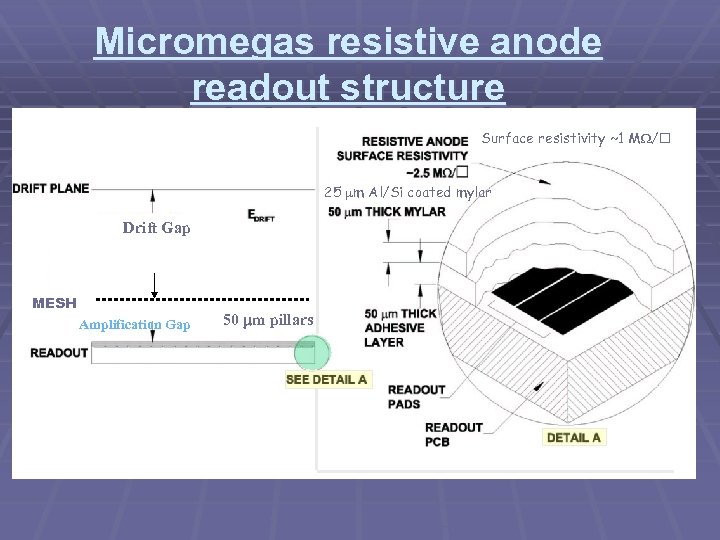Micromegas resistive anode readout structure Surface resistivity ~1 M / 25 m Al/Si coated mylar Drift Gap MESH Amplification Gap 50 m pillars

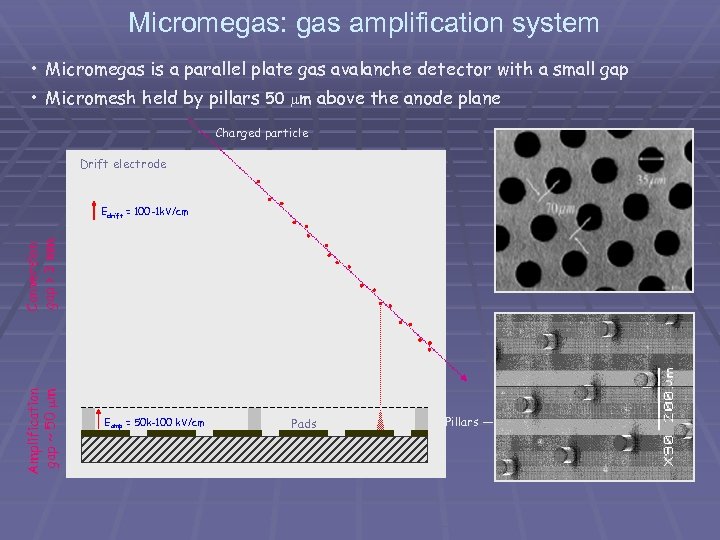Micromegas: gas amplification system • Micromegas is a parallel plate gas avalanche detector with a small gap • Micromesh held by pillars 50 m above the anode plane Charged particle Drift electrode Amplification gap ~ 50 m Conversion gap > 3 mm Edrift = 100 -1 k. V/cm Micromesh Eamp = 50 k-100 k. V/cm Pads ― Pillars ―

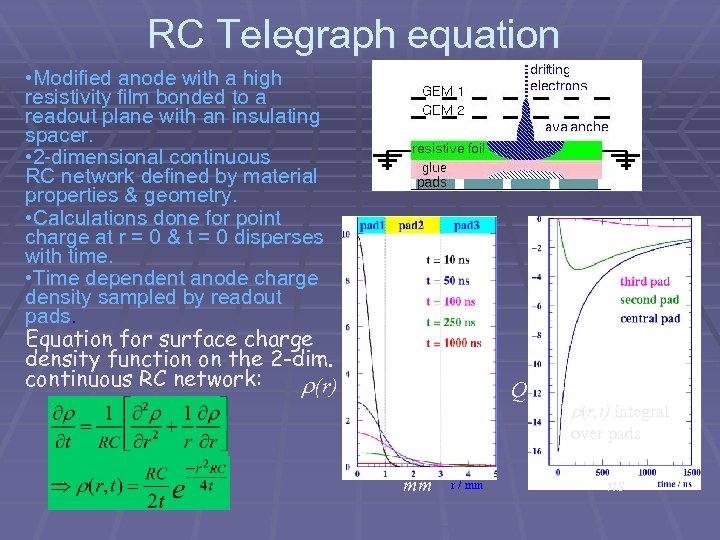RC Telegraph equation • Modified anode with a high resistivity film bonded to a readout plane with an insulating spacer. • 2 -dimensional continuous RC network defined by material properties & geometry. • Calculations done for point charge at r = 0 & t = 0 disperses with time. • Time dependent anode charge density sampled by readout pads. Equation for surface charge density function on the 2 -dim. continuous RC network: (r) Q (r, t) integral over pads mm r / mm ns

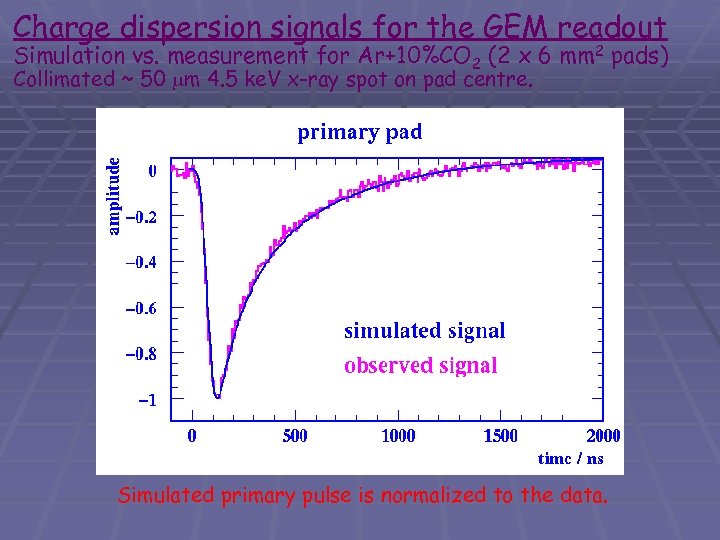Charge dispersion signals for the GEM readout Simulation vs. measurement for Ar+10%CO 2 (2 x 6 mm 2 pads) Collimated ~ 50 m 4. 5 ke. V x-ray spot on pad centre. Simulated primary pulse is normalized to the data.

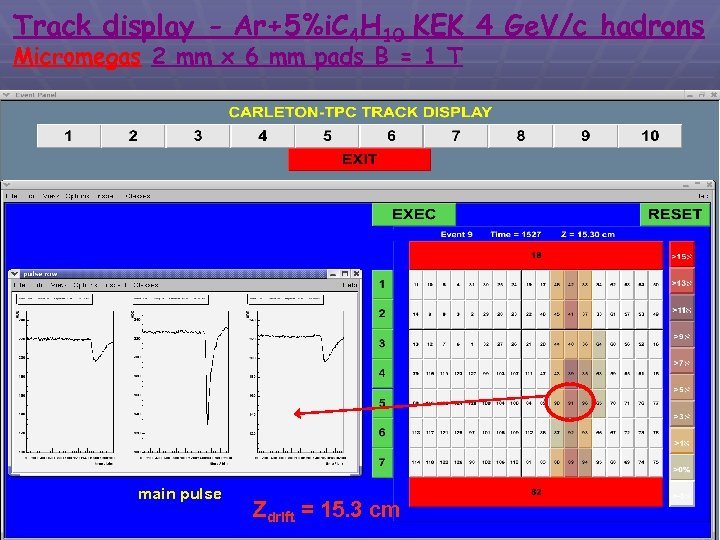Track display - Ar+5%i. C 4 H 10 KEK 4 Ge. V/c hadrons Micromegas 2 mm x 6 mm pads B = 1 T main pulse Zdrift = 15. 3 cm

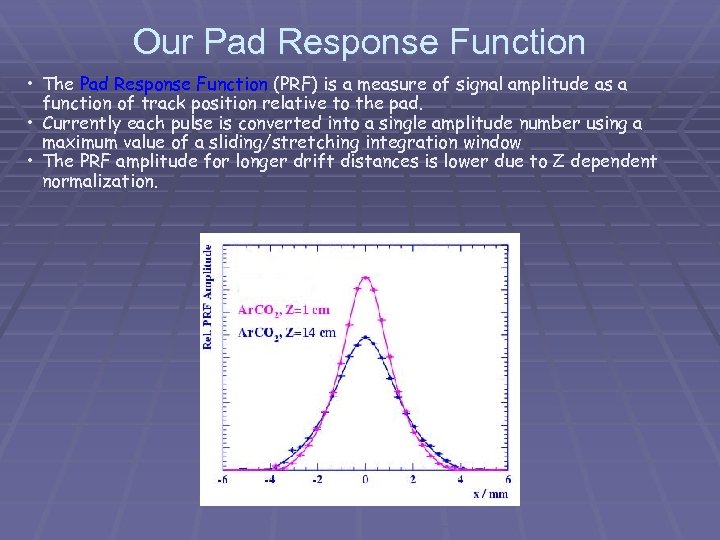Our Pad Response Function • The Pad Response Function (PRF) is a measure of signal amplitude as a function of track position relative to the pad. • Currently each pulse is converted into a single amplitude number using a maximum value of a sliding/stretching integration window • The PRF amplitude for longer drift distances is lower due to Z dependent normalization.

Parameterization of the PRFs • The PRFs are not Gaussian. • The PRF depends on track position relative to the pad: PRF = PRF(x, z). • a 2, a 4, b 2 & b 4 can be written down in terms of: - FWHM = (z) Amplitude • PRFs determined from the data and parameterized by a ratio of two symmetric 4 th order polynomials: - base width (z) of the PRF. The parameters depend on TPC gas and operational setup x/mm

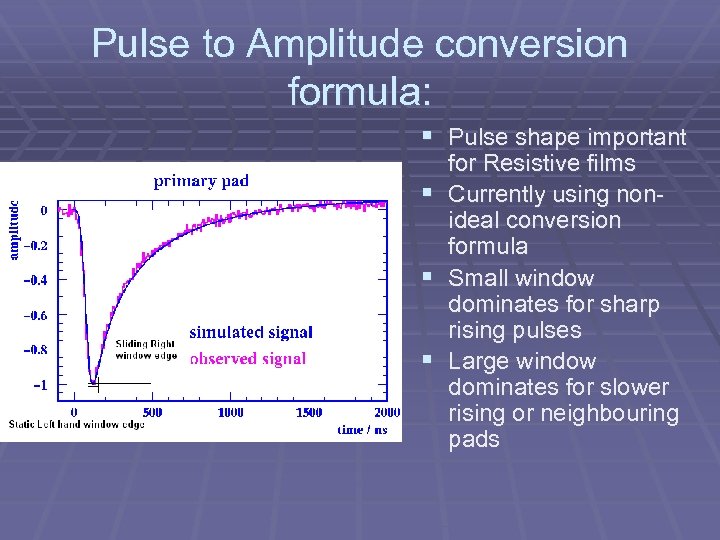Pulse to Amplitude conversion formula: § Pulse shape important for Resistive films § Currently using nonideal conversion formula § Small window dominates for sharp rising pulses § Large window dominates for slower rising or neighbouring pads

Simulation: § Generating fake signal slide including numerical integration formula § Sliding Window signal -> number formula § PRF formula

Simulating the charge dispersion phenomenon M. S. Dixit and A. Rankin, Nucl. Instrum. Methods A 566 (2006) 281. • The charge dispersion equation describe the time evolution of a point like charge deposited on the MPGD resistive anode at t = 0. • To compare with experiment, one needs to include the effects of: • Longitudinal & transverse diffusion in the gas. • Intrinsic rise time Trise of the detector charge pulse. • The effect of preamplifier rise and fall times tr & tf. • And for particle tracks, the effects of primary ionization clustering.

Simulation for a single charge cluster (tracks can be simulated by superposition) The charge density function for a point charge in Cartesian coordinates: Physics effects included in simulation in two parts: 1) as effects which depend on spatial coordinates x & y, or; 2) as effects which depend on time. The spatial effects function includes charge dispersion phenomena & transverse size w of the charge cluster due to transverse diffusion. Qpad(t) is the pad signal from charge dispersion when a charge Nqe of size w is deposited on the anode at t = 0; xhigh, xlow, yhigh, ylow define the pad boundaries &

(2) I(t) incorporates intrinsic rise time, longitudinal diffusion & electronics shaping times as time dependent effects. (1) and (2) are convoluted numerically for the model simulation.

Data: tracks, and reconstruction

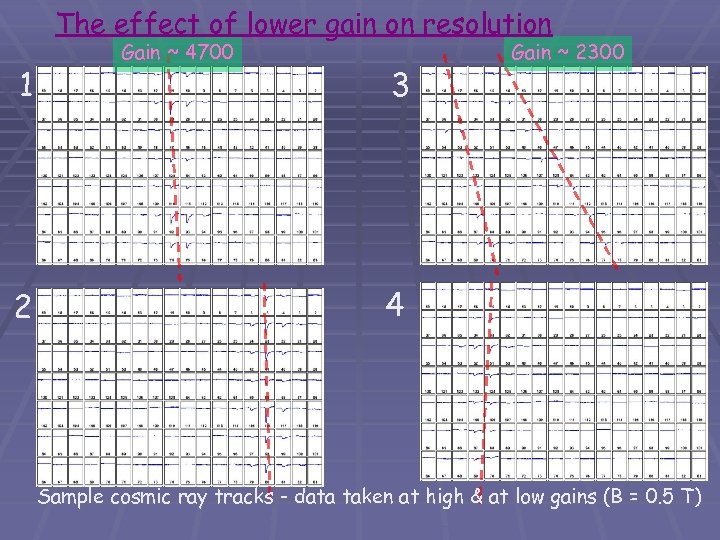The effect of lower gain on resolution 1 2 Gain ~ 4700 3 Gain ~ 2300 4 Sample cosmic ray tracks - data taken at high & at low gains (B = 0. 5 T)

Current track reconstruction method § Step by step run through of data processing § Define Pedestals § Define Time 0 § Take 1/3 – 1/4 data generate PDF § Take another chunk test for calibrating out biases § Remaining for resolution

Results

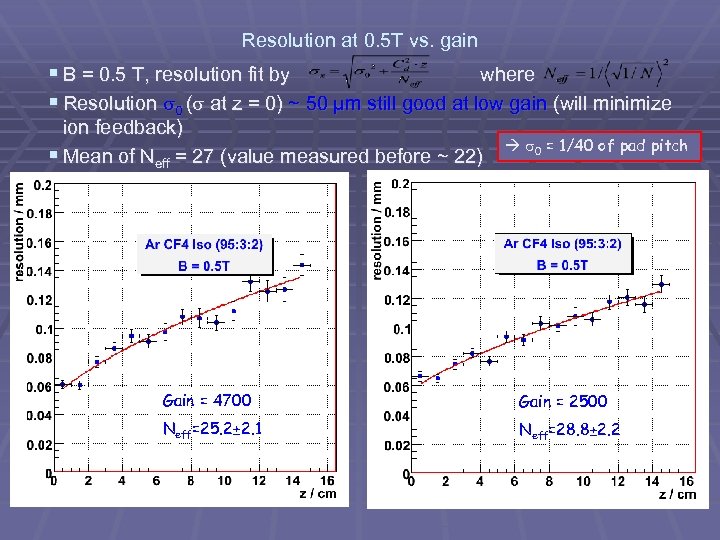Resolution at 0. 5 T vs. gain § B = 0. 5 T, resolution fit by where § Resolution 0 ( at z = 0) ~ 50 µm still good at low gain (will minimize ion feedback) § Mean of Neff = 27 (value measured before ~ 22) 0 = 1/40 of pad pitch Gain = 4700 Gain = 2500 Neff=25. 2± 2. 1 Neff=28. 8± 2. 2

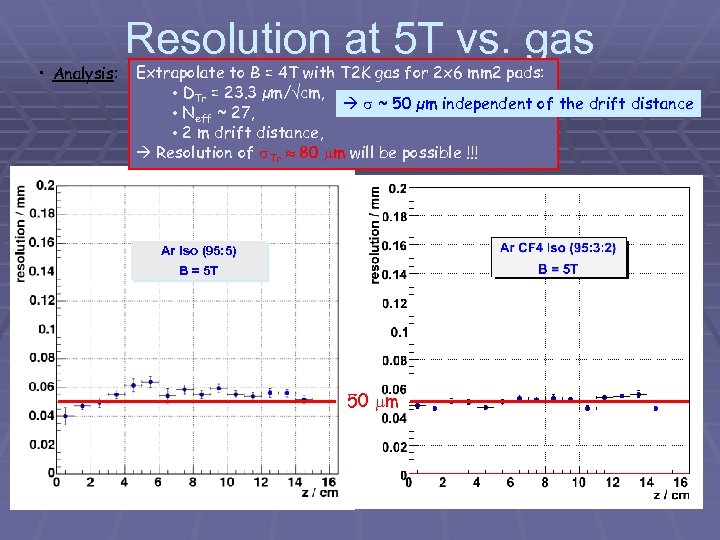Resolution at 5 T vs. gas mixtures • Analysis: -Extrapolate tofit = 4 T with T 2 K gas for 2 x 6 mm 2 pads: Curved track B - EP < • DTr = 23. 3 µm/ cm, ~ 50 µm independent of the drift distance 2 Ge. V Neff (~3°) - |f| < • 0. 05 ~ 27, • 2 m drift distance, Resolution of Tr 80 m will be possible !!! Ar Iso (95: 5) B = 5 T 50 m

Standing Questions § Proposed new data -> Pad Response Value. § Multiple Tracks in single events.

Future holds § Multi Track analysis, runtime Signal extrapolation and subtraction § New signal -> amplitude calculation § Integrate full (set window) signal, and weighted time average (same window) § Incorporate both to give PRF § PRF initial conditions given by simulation rather then guess and chi minimize § Re-write everything in C++ as opposed to Fortran