Скачать презентацию Characterizing millisecond motions in proteins using CPMG-relaxation dispersion Скачать презентацию Characterizing millisecond motions in proteins using CPMG-relaxation dispersion

68cd94841a85bbc3b7af6fb5c05742ed.ppt

  • Количество слайдов: 70

Characterizing millisecond motions in proteins using CPMG-relaxation dispersion measurements Tony Mittermaier Mc. Gill Aug, Characterizing millisecond motions in proteins using CPMG-relaxation dispersion measurements Tony Mittermaier Mc. Gill Aug, 2007 CCPN

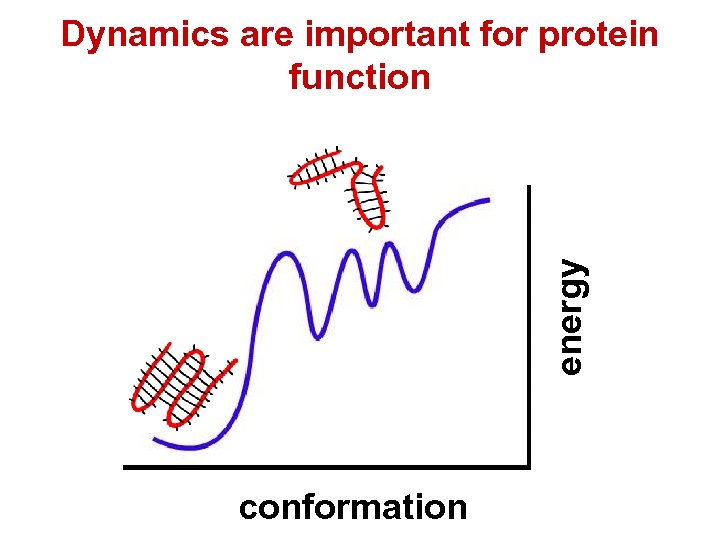energy Dynamics are important for protein function conformation energy Dynamics are important for protein function conformation

Two-site conformational exchange • Weakly populated protein states are often not directly observable in Two-site conformational exchange • Weakly populated protein states are often not directly observable in NMR spectra.

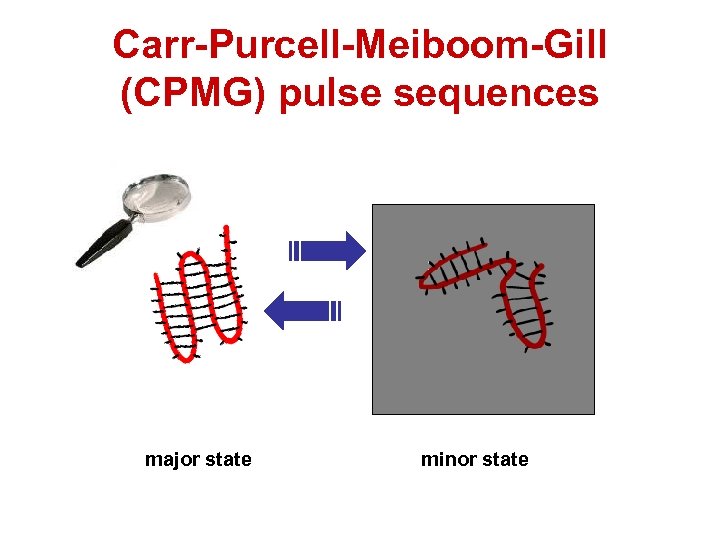Carr-Purcell-Meiboom-Gill (CPMG) pulse sequences major state minor state Carr-Purcell-Meiboom-Gill (CPMG) pulse sequences major state minor state

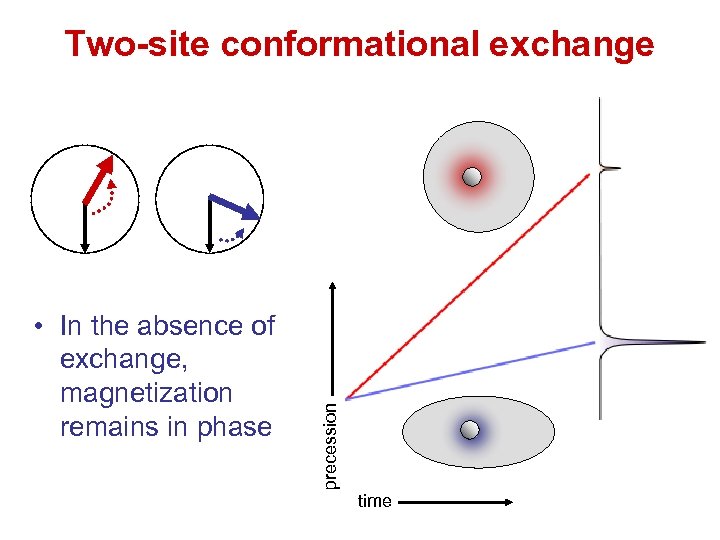• In the absence of exchange, magnetization remains in phase precession Two-site conformational • In the absence of exchange, magnetization remains in phase precession Two-site conformational exchange time

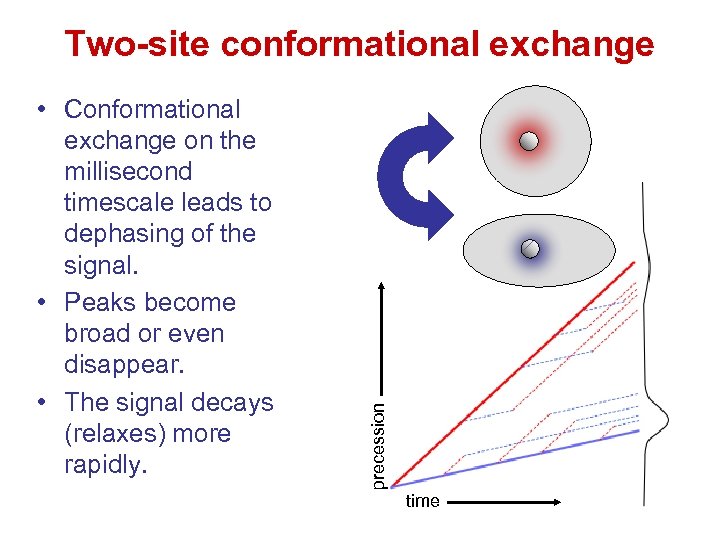• Conformational exchange on the millisecond timescale leads to dephasing of the signal. • Conformational exchange on the millisecond timescale leads to dephasing of the signal. • Peaks become broad or even disappear. • The signal decays (relaxes) more rapidly. precession Two-site conformational exchange time

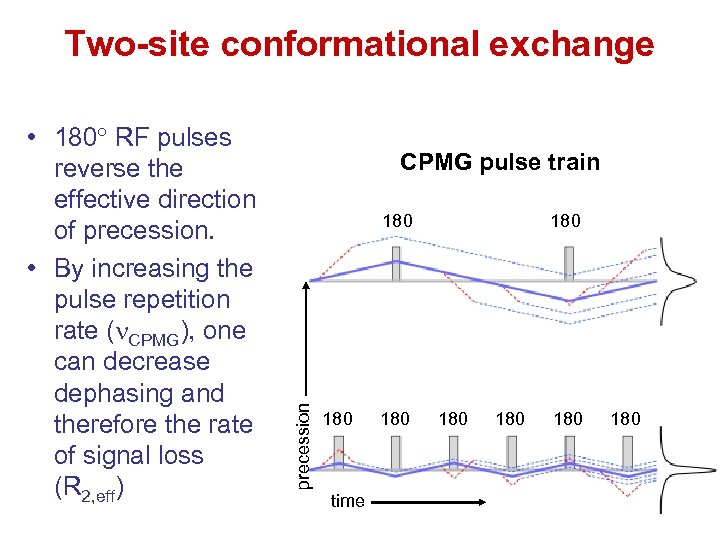Two-site conformational exchange CPMG pulse train 180 precession • 180 RF pulses reverse the Two-site conformational exchange CPMG pulse train 180 precession • 180 RF pulses reverse the effective direction of precession. • By increasing the pulse repetition rate (n. CPMG), one can decrease dephasing and therefore the rate of signal loss (R 2, eff) 180 time 180 180 180

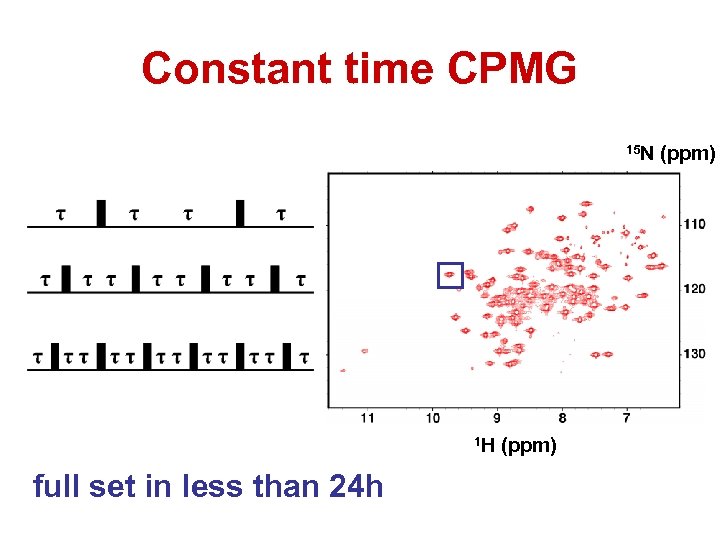Constant time CPMG 15 N 1 H full set in less than 24 h Constant time CPMG 15 N 1 H full set in less than 24 h (ppm)

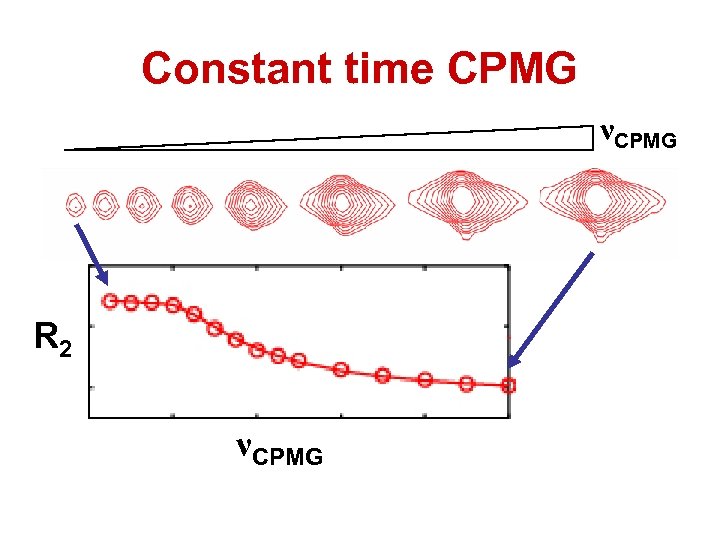Constant time CPMG νCPMG R 2 νCPMG Constant time CPMG νCPMG R 2 νCPMG

Two-site exchange equations R 2 ωA νCPMG ωB Two-site exchange equations R 2 ωA νCPMG ωB

Two-site exchange equations General equation: We can extract k. AB k. BA Δω2 separately Two-site exchange equations General equation: We can extract k. AB k. BA Δω2 separately Carver & Richards, R. E. J. Magn. Reson 1972 6 89

Two-site exchange equations Fast timescale: kex>>Δω We can extract kex p. B and Δω Two-site exchange equations Fast timescale: kex>>Δω We can extract kex p. B and Δω appear in the same term: inseparable. Meiboom, Luz & D. Gill J. Chem. Phys. 1957 27 1411.

Two-site exchange equations Slow timescale: kex<<Δω Curve is independent of k. BA We can Two-site exchange equations Slow timescale: kex<<Δω Curve is independent of k. BA We can only extract k. AB and Δω2 Tollinger et. al J Am Chem Soc. 2001 123 11341.

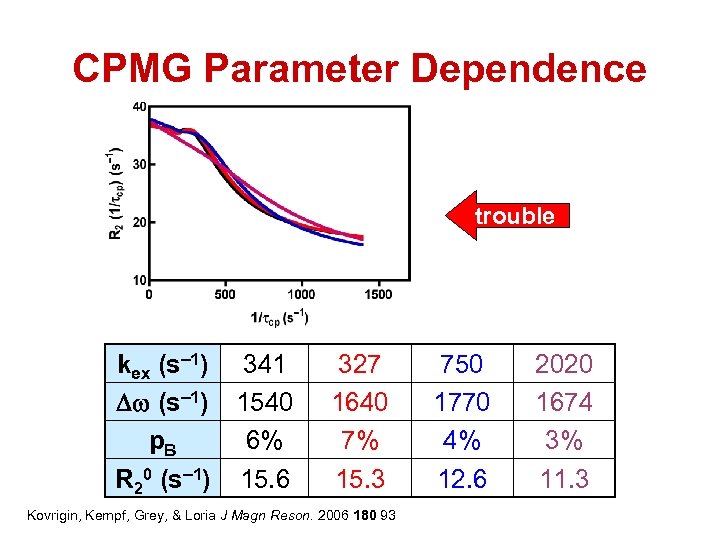CPMG Parameter Dependence trouble kex (s– 1) 341 Dw (s– 1) 1540 p. B CPMG Parameter Dependence trouble kex (s– 1) 341 Dw (s– 1) 1540 p. B 6% R 20 (s– 1) 15. 6 327 1640 7% 15. 3 Kovrigin, Kempf, Grey, & Loria J Magn Reson. 2006 180 93 750 1770 4% 12. 6 2020 1674 3% 11. 3

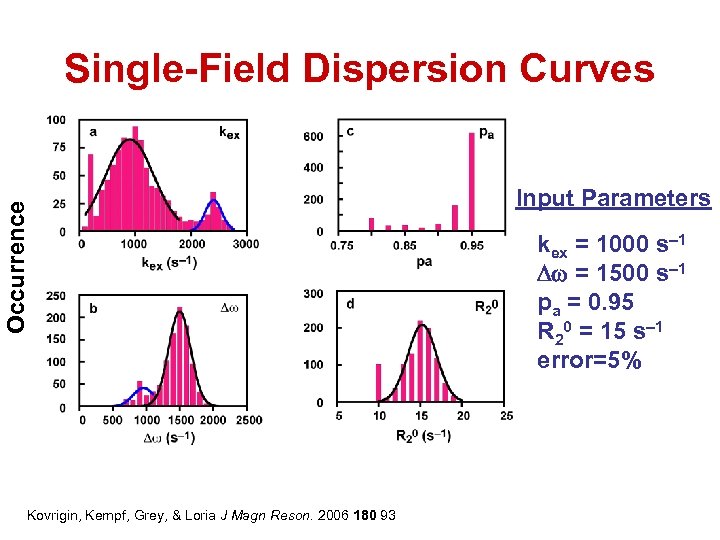Occurrence Single-Field Dispersion Curves Kovrigin, Kempf, Grey, & Loria J Magn Reson. 2006 180 Occurrence Single-Field Dispersion Curves Kovrigin, Kempf, Grey, & Loria J Magn Reson. 2006 180 93 Input Parameters kex = 1000 s– 1 Dw = 1500 s– 1 pa = 0. 95 R 20 = 15 s– 1 error=5%

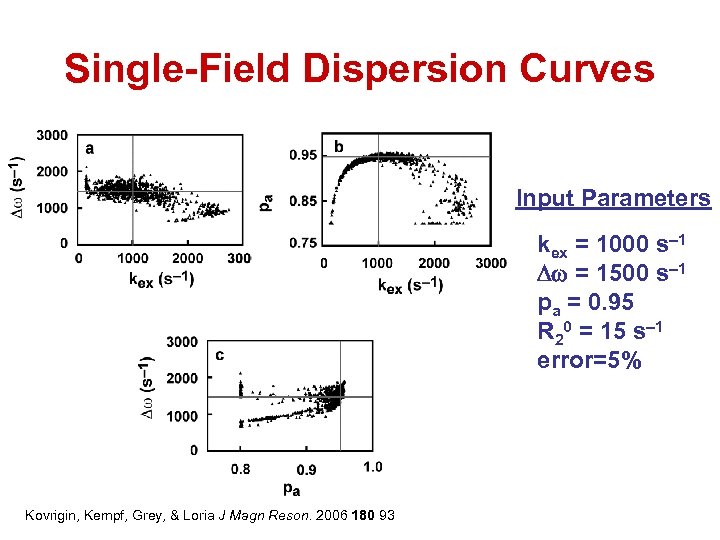Single-Field Dispersion Curves Input Parameters kex = 1000 s– 1 Dw = 1500 s– Single-Field Dispersion Curves Input Parameters kex = 1000 s– 1 Dw = 1500 s– 1 pa = 0. 95 R 20 = 15 s– 1 error=5% Kovrigin, Kempf, Grey, & Loria J Magn Reson. 2006 180 93

Single-Field Dispersion Curves • We need additional non-redundant data to resolve ambiguity in dispersion Single-Field Dispersion Curves • We need additional non-redundant data to resolve ambiguity in dispersion curves. kex field independent p. A field independent Δω field dependent = Δω(ppm)*ωspectrometer(MHz)

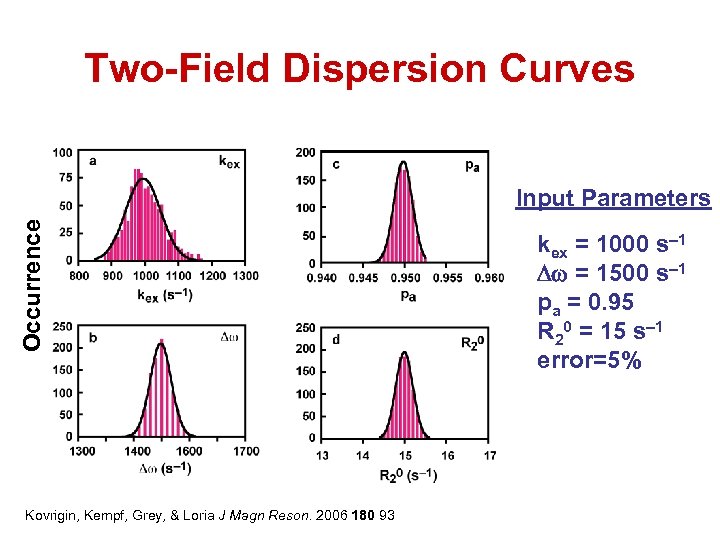Two-Field Dispersion Curves Occurrence Input Parameters Kovrigin, Kempf, Grey, & Loria J Magn Reson. Two-Field Dispersion Curves Occurrence Input Parameters Kovrigin, Kempf, Grey, & Loria J Magn Reson. 2006 180 93 kex = 1000 s– 1 Dw = 1500 s– 1 pa = 0. 95 R 20 = 15 s– 1 error=5%

From CPMG data to protein motions R 2, eff νCPMG p. B kex From CPMG data to protein motions R 2, eff νCPMG p. B kex

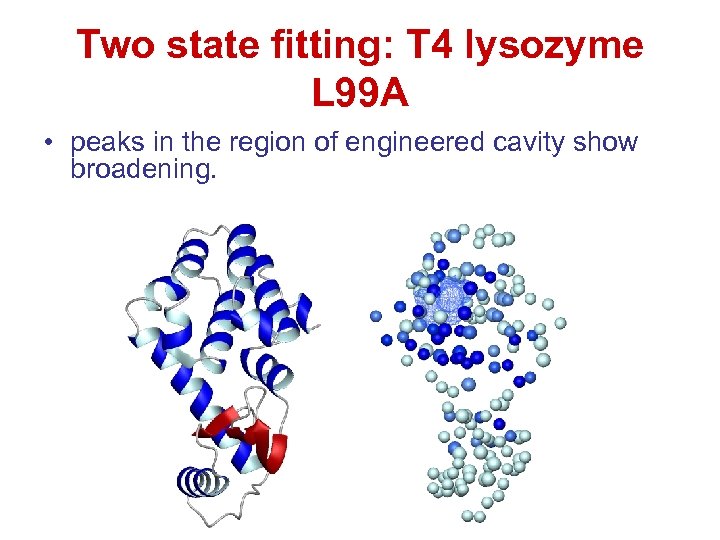Two state fitting: T 4 lysozyme L 99 A • peaks in the region Two state fitting: T 4 lysozyme L 99 A • peaks in the region of engineered cavity show broadening.

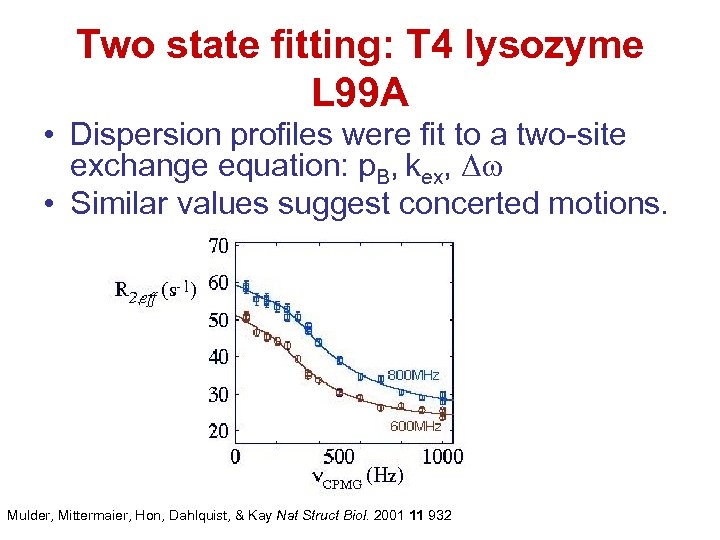Two state fitting: T 4 lysozyme L 99 A • Dispersion profiles were fit Two state fitting: T 4 lysozyme L 99 A • Dispersion profiles were fit to a two-site exchange equation: p. B, kex, Δω • Similar values suggest concerted motions. Mulder, Mittermaier, Hon, Dahlquist, & Kay Nat Struct Biol. 2001 11 932

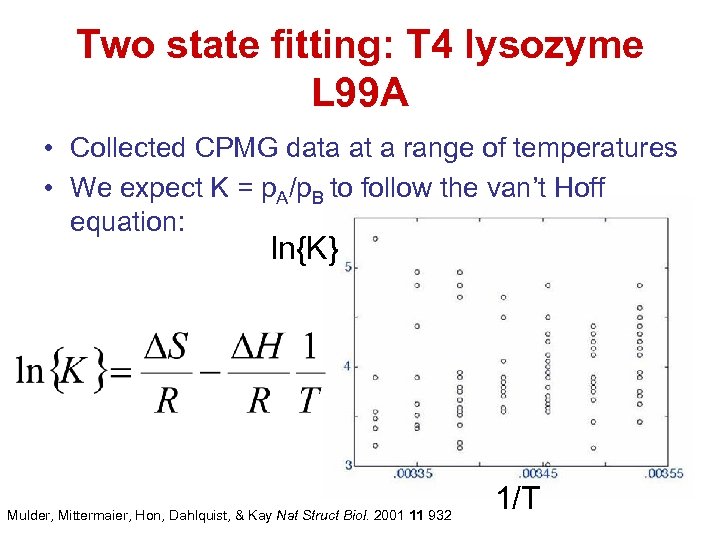Two state fitting: T 4 lysozyme L 99 A • Collected CPMG data at Two state fitting: T 4 lysozyme L 99 A • Collected CPMG data at a range of temperatures • We expect K = p. A/p. B to follow the van’t Hoff equation: ln{K} Mulder, Mittermaier, Hon, Dahlquist, & Kay Nat Struct Biol. 2001 11 932 1/T

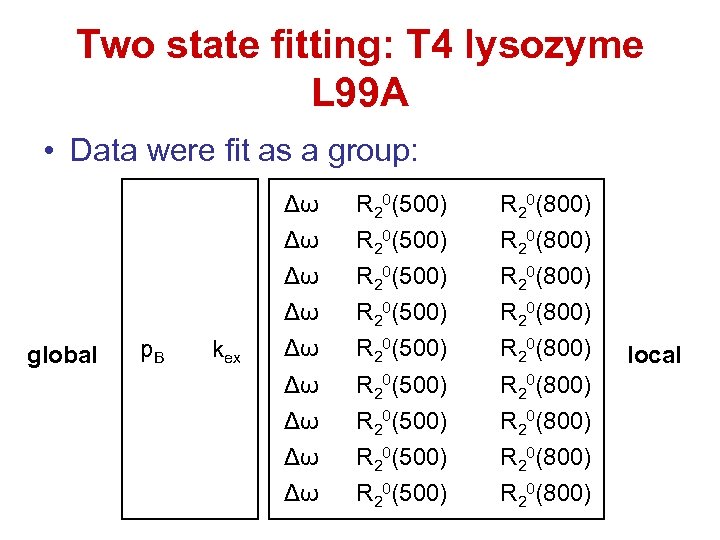Two state fitting: T 4 lysozyme L 99 A • Data were fit as Two state fitting: T 4 lysozyme L 99 A • Data were fit as a group: p. B Δω R 20(500) R 20(800) p. B kex Δω R 20(500) R 20(800) p. B global kex Δω R 20(500) R 20(800) p. B kex Δω R 20(500) R 20(800) local

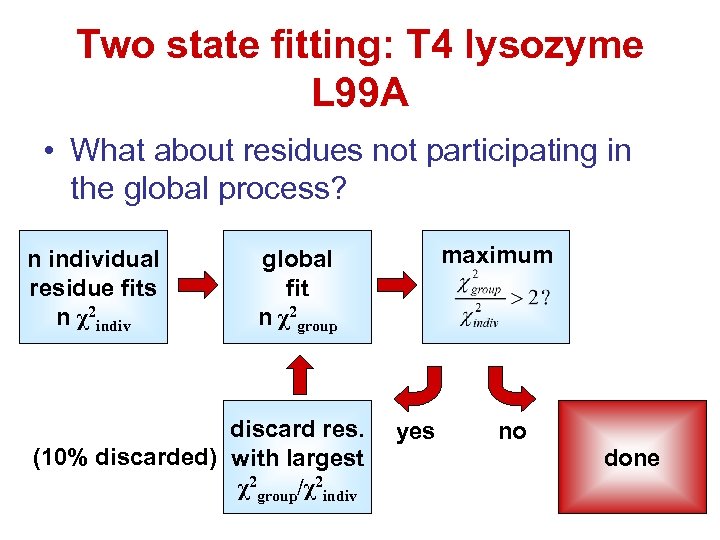Two state fitting: T 4 lysozyme L 99 A • What about residues not Two state fitting: T 4 lysozyme L 99 A • What about residues not participating in the global process? n individual residue fits n χ2 indiv maximum global fit n χ2 group discard res. (10% discarded) with largest χ2 group/χ2 indiv yes no done

Two state fitting: T 4 lysozyme L 99 A • Experimental data are in Two state fitting: T 4 lysozyme L 99 A • Experimental data are in good agreement with global fit. CH 3 ( 2) 600 MHz CH 3 ( 2) 800 MHz R 2, eff (s-1) T (°C) CPMG (Hz) NH 500 MHz NH 800 MHz

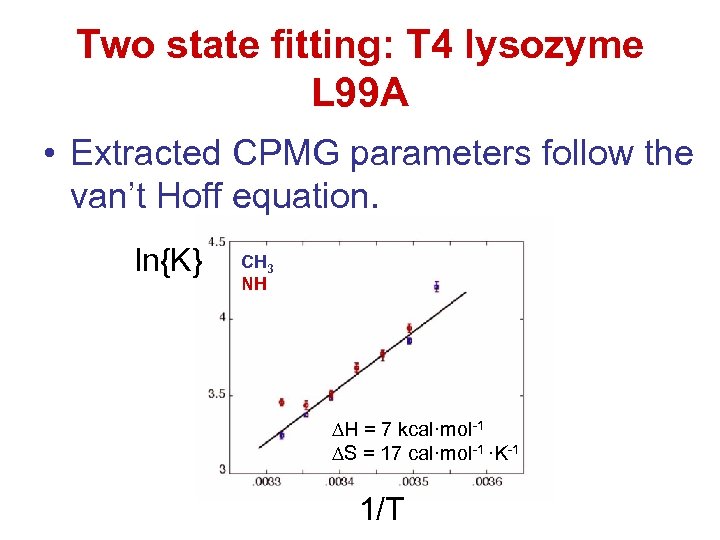Two state fitting: T 4 lysozyme L 99 A • Extracted CPMG parameters follow Two state fitting: T 4 lysozyme L 99 A • Extracted CPMG parameters follow the van’t Hoff equation. ln{K} CH 3 NH H = 7 kcal·mol-1 S = 17 cal·mol-1 ·K-1 1/T

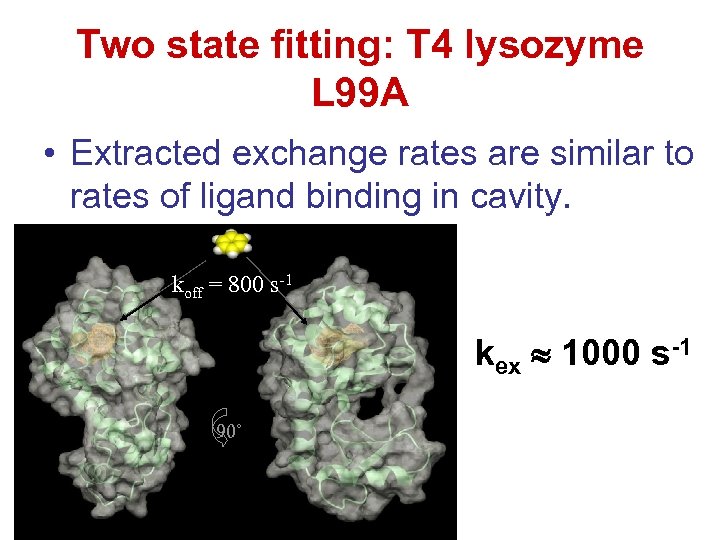Two state fitting: T 4 lysozyme L 99 A • Extracted exchange rates are Two state fitting: T 4 lysozyme L 99 A • Extracted exchange rates are similar to rates of ligand binding in cavity. koff = 800 s-1 kex 1000 s-1 90˚

Two state fitting: T 4 lysozyme L 99 A • We could just average Two state fitting: T 4 lysozyme L 99 A • We could just average p. B values over all residues, but there are several drawbacks: – The average value of p. B will not in general correspond to a best fit to experimental data. – It is difficult to identify residues that do not participate in the global process. – Residues in fast exchange do not provide p. B, however kex is global, refines the fit. p. Ap. B(Δω)2 kex fast exchange p. B Δω kex intermediate exchange

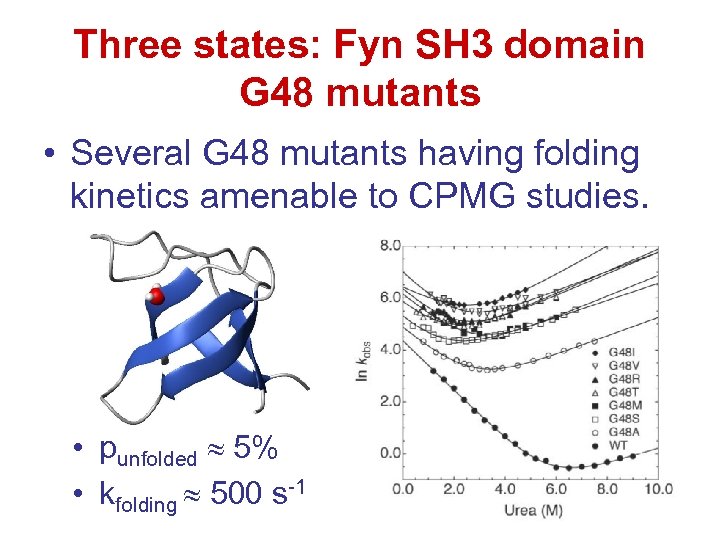Three states: Fyn SH 3 domain G 48 mutants • Several G 48 mutants Three states: Fyn SH 3 domain G 48 mutants • Several G 48 mutants having folding kinetics amenable to CPMG studies. • punfolded 5% • kfolding 500 s-1

log 10{kf} Three states: Fyn SH 3 domain G 48 mutants log 10{ku} • log 10{kf} Three states: Fyn SH 3 domain G 48 mutants log 10{ku} • residues have very different G 48 M apparent ku & kf • elimination based on χ2 group/χ2 indiv discards ≈ 50% data. G 48 V • folding is not two state. Korzhnev, Salvatella, Vendruscolo, Di Nardo, Davidson, Dobson, & Kay LE Nature. 2004 430 586

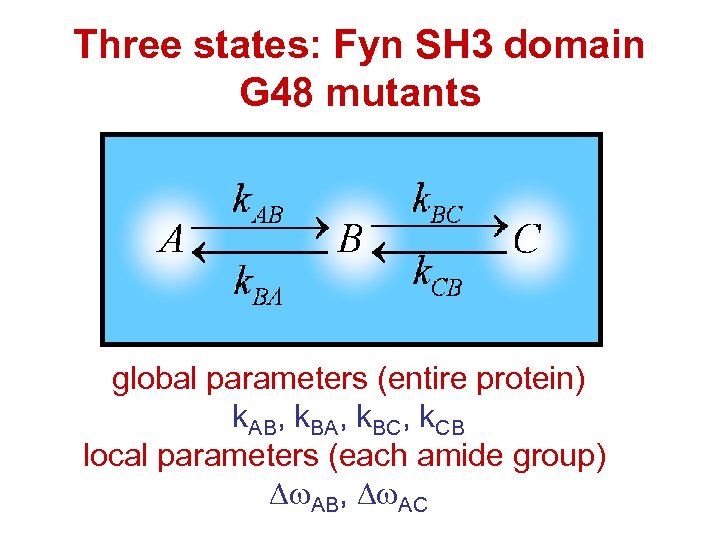Three states: Fyn SH 3 domain G 48 mutants global parameters (entire protein) k. Three states: Fyn SH 3 domain G 48 mutants global parameters (entire protein) k. AB, k. BA, k. BC, k. CB local parameters (each amide group) AB, AC

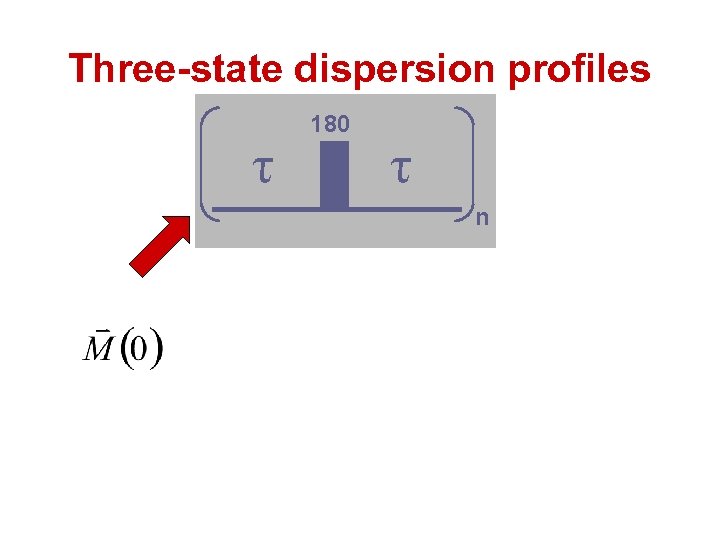
Three-state dispersion profiles • Two-state exchange described by analytical expressions. • Three-state exchange profiles Three-state dispersion profiles • Two-state exchange described by analytical expressions. • Three-state exchange profiles can be calculated numerically using modified Bloch-Mc. Connell equations.

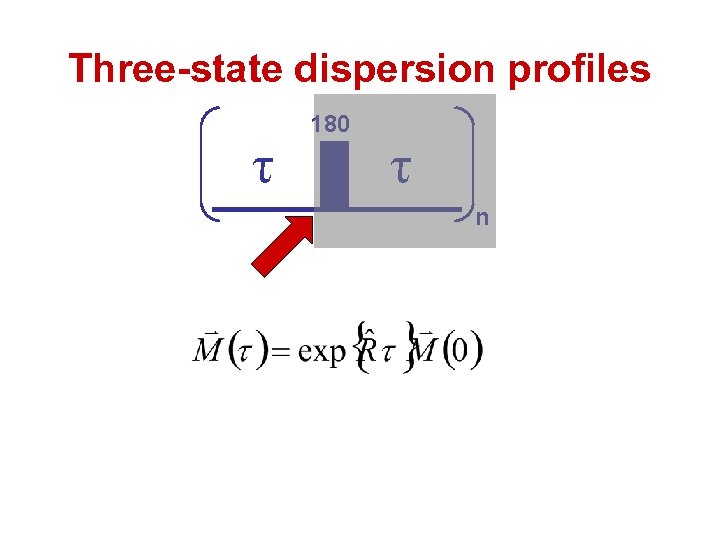
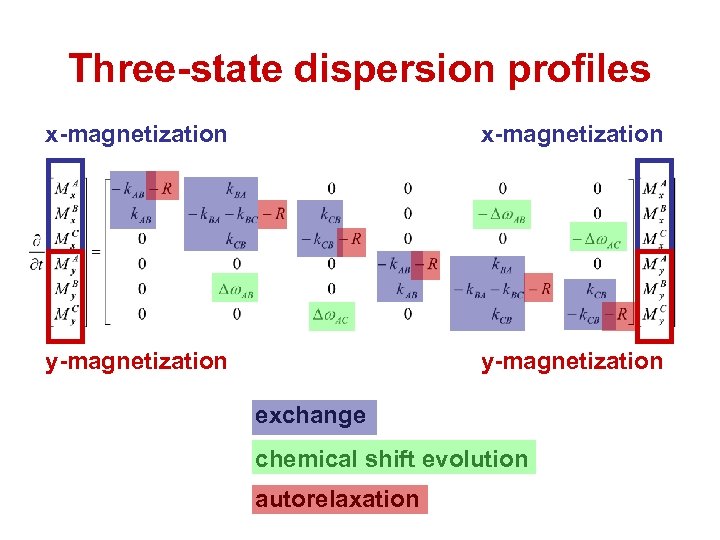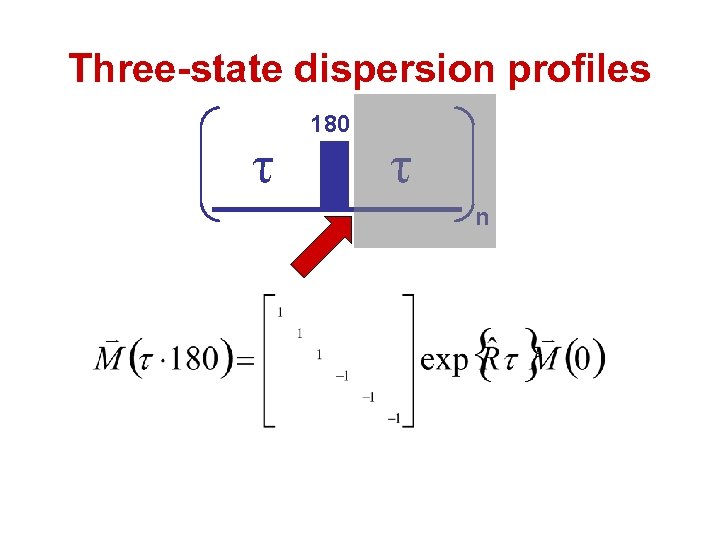
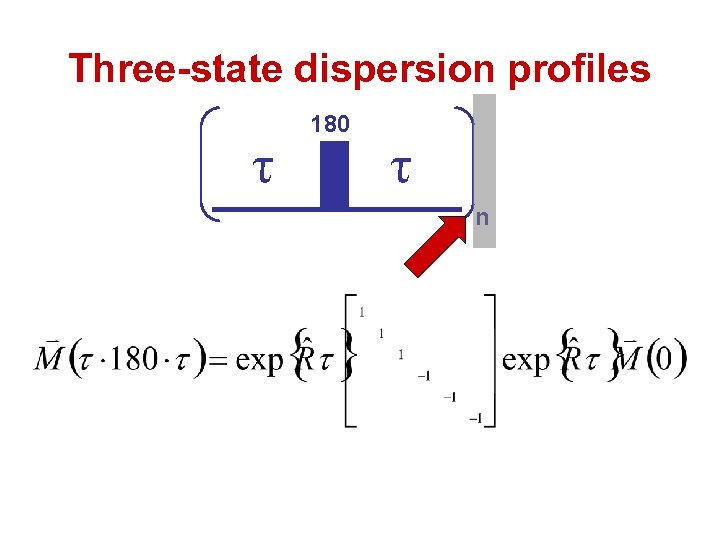
Three-state dispersion profiles x-magnetization y-magnetization exchange chemical shift evolution autorelaxation 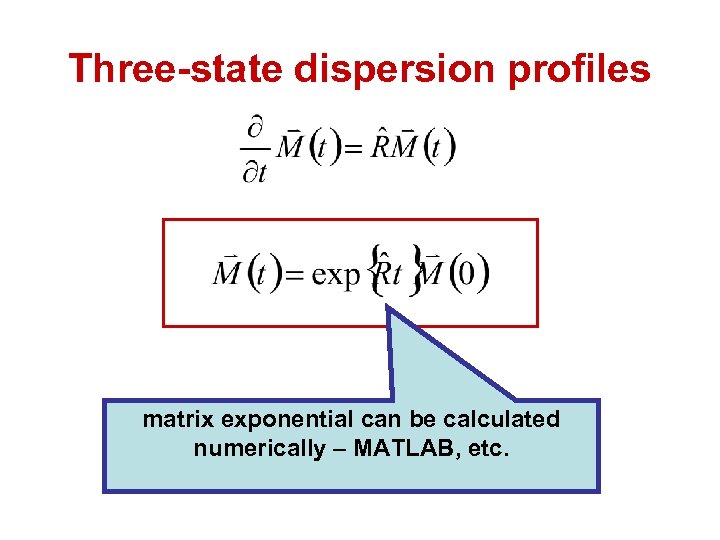Three-state dispersion profiles x-magnetization y-magnetization exchange chemical shift evolution autorelaxation

Three-state dispersion profiles matrix exponential can be calculated numerically – MATLAB, etc. Three-state dispersion profiles matrix exponential can be calculated numerically – MATLAB, etc.

Three-state dispersion profiles τ 180 τ n Three-state dispersion profiles τ 180 τ n

Three-state dispersion profiles τ 180 τ n Three-state dispersion profiles τ 180 τ n

Three-state dispersion profiles τ 180 τ n Three-state dispersion profiles τ 180 τ n

Three-state dispersion profiles τ 180 τ n Three-state dispersion profiles τ 180 τ n

Three-state dispersion profiles τ 180 τ n Three-state dispersion profiles τ 180 τ n

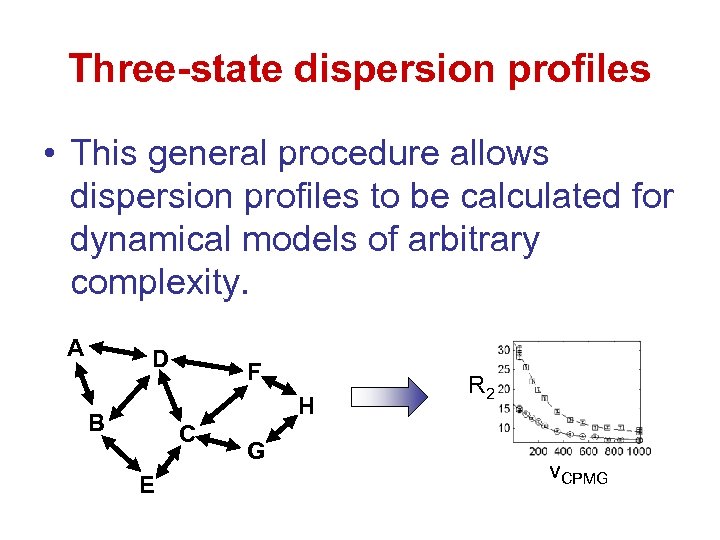Three-state dispersion profiles • This general procedure allows dispersion profiles to be calculated for Three-state dispersion profiles • This general procedure allows dispersion profiles to be calculated for dynamical models of arbitrary complexity. A D F H B C E G R 2 v. CPMG

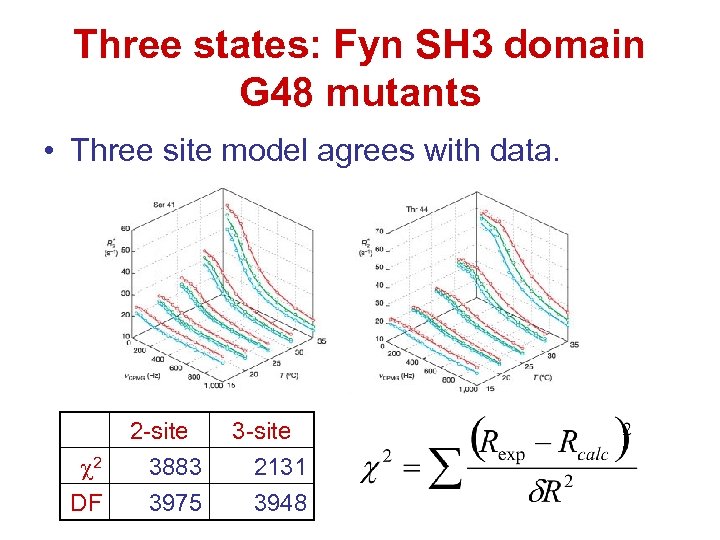Three states: Fyn SH 3 domain G 48 mutants • Three site model agrees Three states: Fyn SH 3 domain G 48 mutants • Three site model agrees with data. 2 DF 2 -site 3883 3975 3 -site 2131 3948

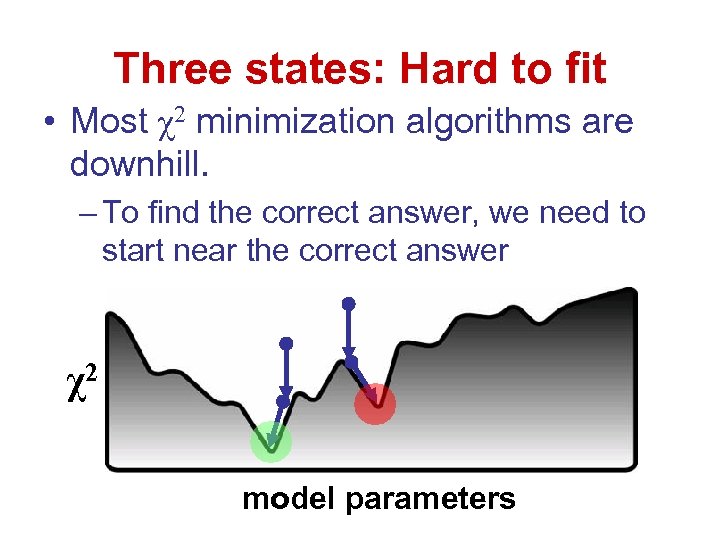Three states: Hard to fit • Most χ2 minimization algorithms are downhill. – To Three states: Hard to fit • Most χ2 minimization algorithms are downhill. – To find the correct answer, we need to start near the correct answer χ2 model parameters

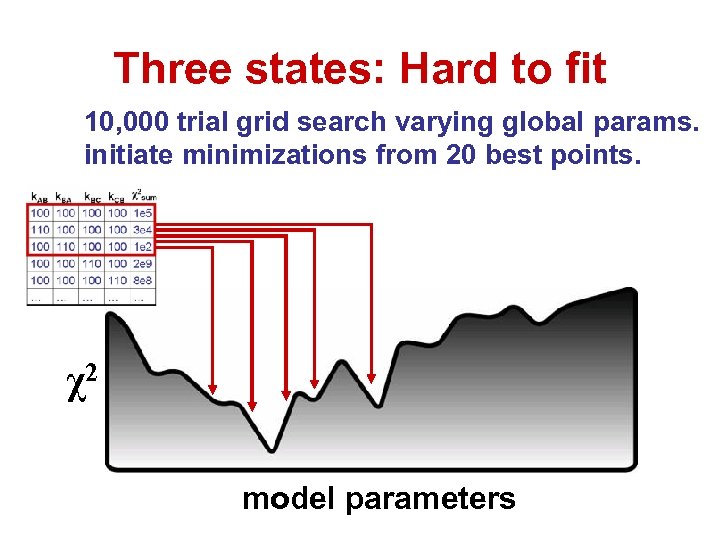Three states: Hard to fit 10, 000 trial grid search varying global params. initiate Three states: Hard to fit 10, 000 trial grid search varying global params. initiate minimizations from 20 best points. χ2 model parameters

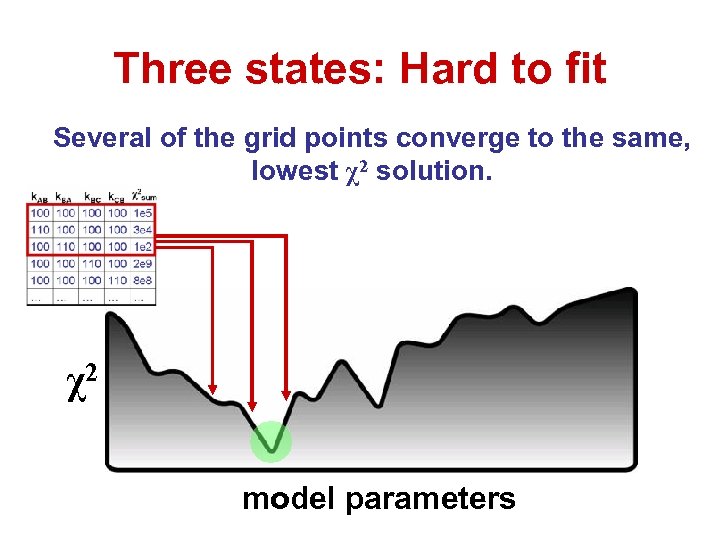Three states: Hard to fit Several of the grid points converge to the same, Three states: Hard to fit Several of the grid points converge to the same, lowest χ2 solution. χ2 model parameters

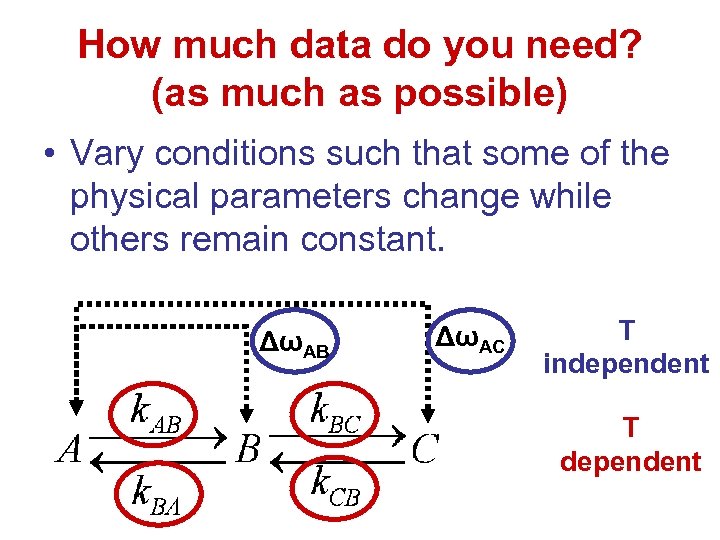How much data do you need? (as much as possible) • Vary conditions such How much data do you need? (as much as possible) • Vary conditions such that some of the physical parameters change while others remain constant. ΔωAB ΔωAC T independent T dependent

How much data do you need? (as much as possible) • Vary conditions such How much data do you need? (as much as possible) • Vary conditions such that some of the physical parameters change while others remain constant. only one rate depends on [L]

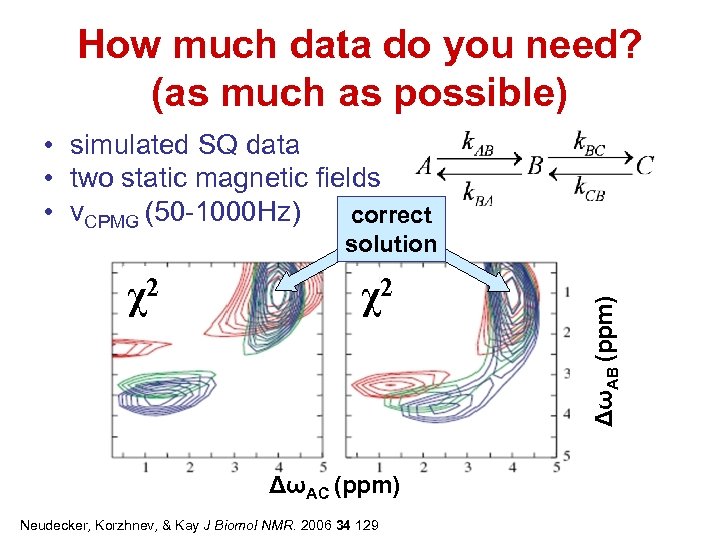How much data do you need? (as much as possible) • simulated SQ data How much data do you need? (as much as possible) • simulated SQ data • two static magnetic fields • νCPMG (50 -1000 Hz) correct χ2 χ2 ΔωAC (ppm) Neudecker, Korzhnev, & Kay J Biomol NMR. 2006 34 129 ΔωAB (ppm) solution

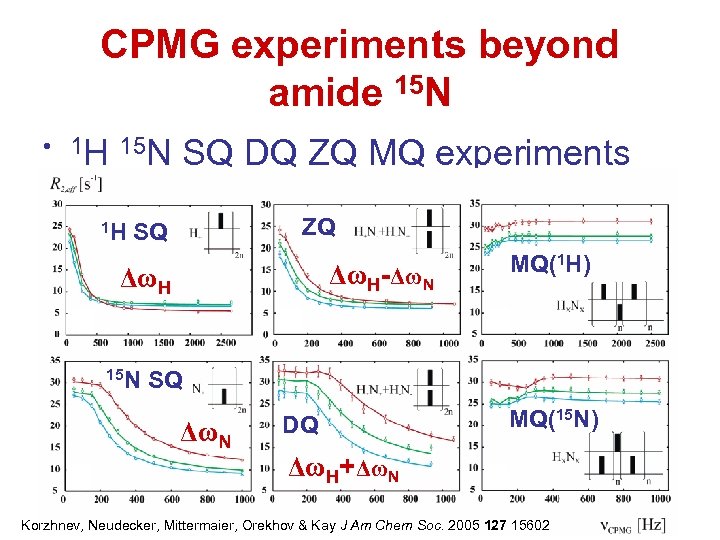CPMG experiments beyond amide 15 N • 1 H 15 N 1 H SQ CPMG experiments beyond amide 15 N • 1 H 15 N 1 H SQ DQ ZQ MQ experiments ZQ SQ ΔωH-ΔωN ΔωH 15 N MQ(1 H) SQ ΔωN DQ MQ(15 N) ΔωH+ΔωN Korzhnev, Neudecker, Mittermaier, Orekhov & Kay J Am Chem Soc. 2005 127 15602

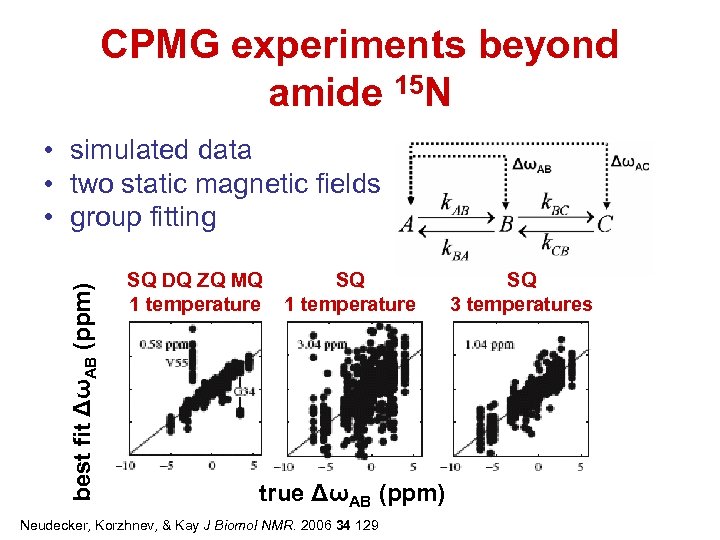CPMG experiments beyond amide 15 N best fit ΔωAB (ppm) • simulated data • CPMG experiments beyond amide 15 N best fit ΔωAB (ppm) • simulated data • two static magnetic fields • group fitting SQ DQ ZQ MQ 1 temperature SQ 1 temperature true ΔωAB (ppm) Neudecker, Korzhnev, & Kay J Biomol NMR. 2006 34 129 SQ 3 temperatures

CPMG experiments beyond amide 15 N • In general, dispersion profiles are well-fit by CPMG experiments beyond amide 15 N • In general, dispersion profiles are well-fit by two-site model. • Even with 6 experiments, for singleresidue fits, 3 -site is better than 2 -site model for only 14 out of 40 residues. • Multi-site models explain inconsistencies between apparent two-site parameters for different residues.

Characterizing minor states using CPMG chemical shift information Characterizing minor states using CPMG chemical shift information

Obtaining the signs of chemical shift differences 15 N ±Dw ? 1 H ppm Obtaining the signs of chemical shift differences 15 N ±Dw ? 1 H ppm

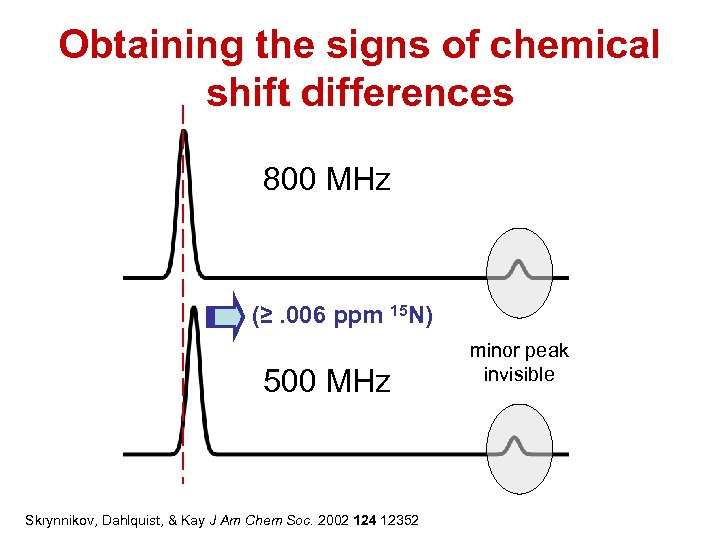Obtaining the signs of chemical shift differences 800 MHz (≥. 006 ppm 15 N) Obtaining the signs of chemical shift differences 800 MHz (≥. 006 ppm 15 N) 500 MHz Skrynnikov, Dahlquist, & Kay J Am Chem Soc. 2002 124 12352 minor peak invisible

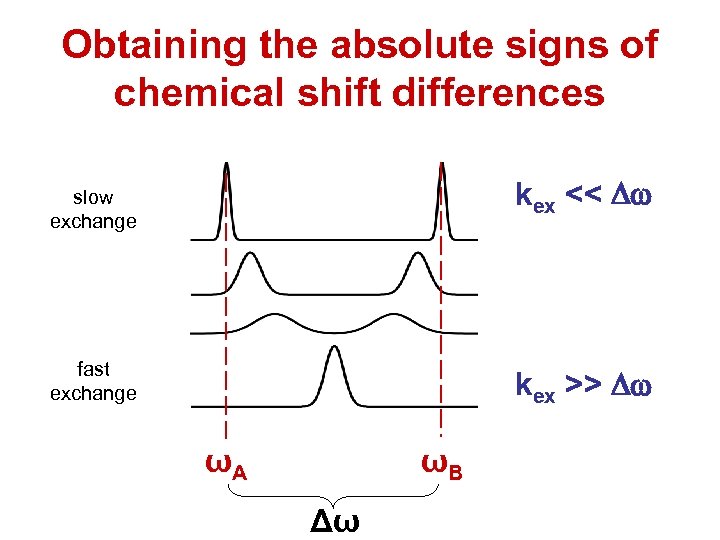Obtaining the absolute signs of chemical shift differences kex << Dw slow exchange fast Obtaining the absolute signs of chemical shift differences kex << Dw slow exchange fast exchange kex >> Dw ωA ωB Δω

Obtaining the signs of chemical shift differences • In the case of three-site exchange Obtaining the signs of chemical shift differences • In the case of three-site exchange the situation is a little more complicated but analogous. coherence in states A, B &C • Imaginary parts of eigenvalues of R give the peak locations. Korzhnev, Neudecker, Mittermaier, Orekhov & Kay J Am Chem Soc. 2005 127 15602

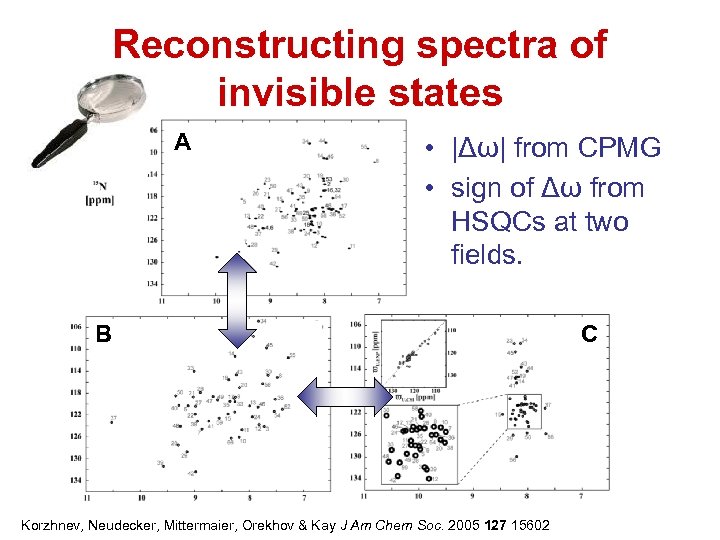Reconstructing spectra of invisible states A • |Δω| from CPMG • sign of Δω Reconstructing spectra of invisible states A • |Δω| from CPMG • sign of Δω from HSQCs at two fields. B Korzhnev, Neudecker, Mittermaier, Orekhov & Kay J Am Chem Soc. 2005 127 15602 C

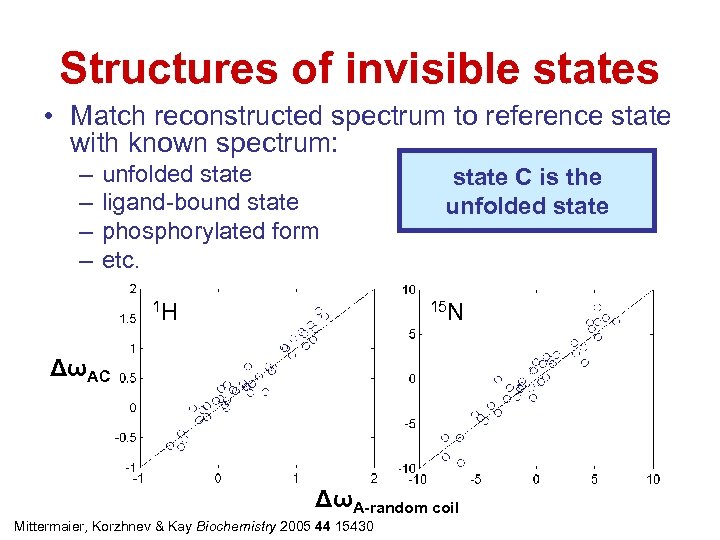Structures of invisible states • Match reconstructed spectrum to reference state with known spectrum: Structures of invisible states • Match reconstructed spectrum to reference state with known spectrum: – – unfolded state ligand-bound state phosphorylated form etc. 1 H state C is the unfolded state 15 N ΔωAC ΔωA-random coil Mittermaier, Korzhnev & Kay Biochemistry 2005 44 15430

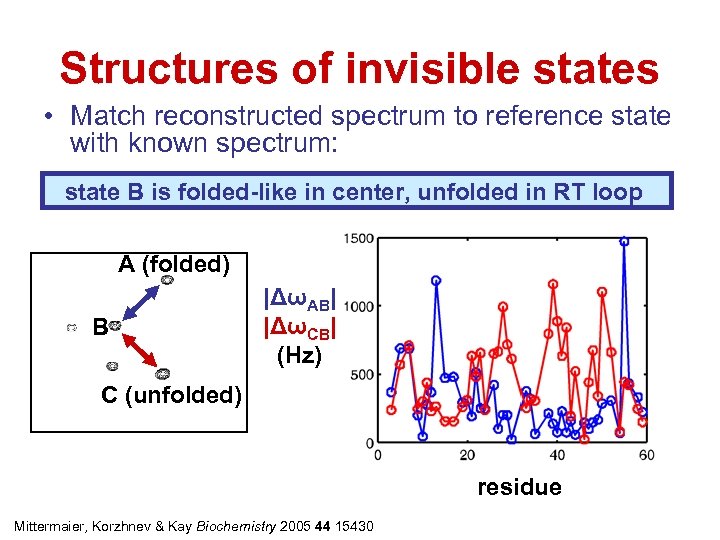Structures of invisible states • Match reconstructed spectrum to reference state with known spectrum: Structures of invisible states • Match reconstructed spectrum to reference state with known spectrum: state B is folded-like in center, unfolded in RT loop A (folded) B |ΔωAB| |ΔωCB| (Hz) C (unfolded) residue Mittermaier, Korzhnev & Kay Biochemistry 2005 44 15430

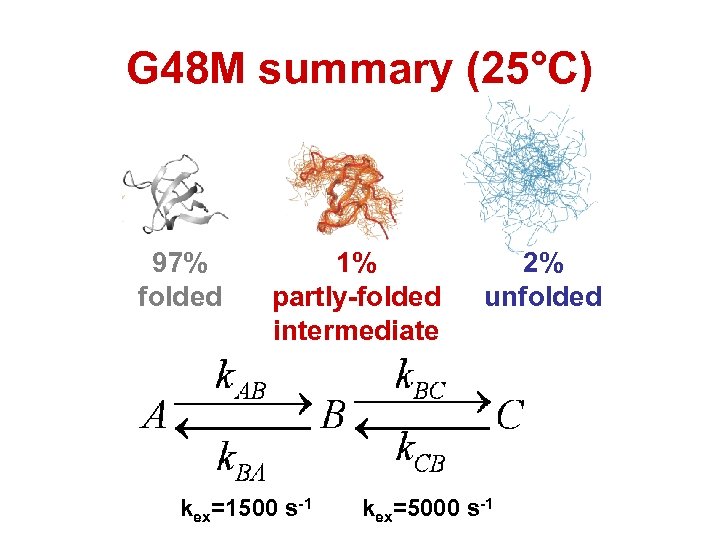G 48 M summary (25°C) 97% folded 1% partly-folded intermediate kex=1500 s-1 2% unfolded G 48 M summary (25°C) 97% folded 1% partly-folded intermediate kex=1500 s-1 2% unfolded kex=5000 s-1

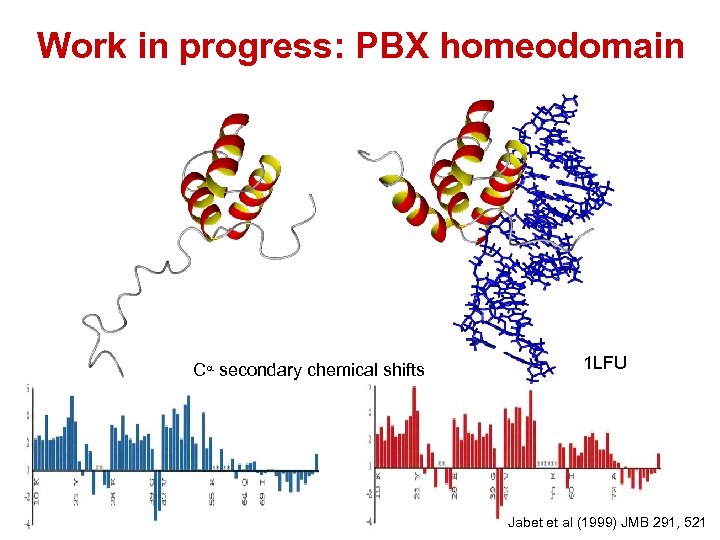Work in progress: PBX homeodomain Ca secondary chemical shifts 1 LFU Jabet et al Work in progress: PBX homeodomain Ca secondary chemical shifts 1 LFU Jabet et al (1999) JMB 291, 521

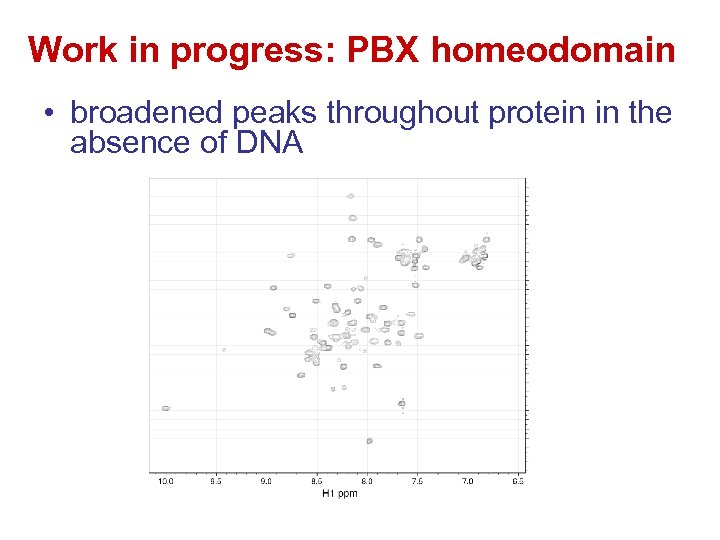Work in progress: PBX homeodomain • broadened peaks throughout protein in the absence of Work in progress: PBX homeodomain • broadened peaks throughout protein in the absence of DNA

Work in progress: PBX homeodomain ? Work in progress: PBX homeodomain ?

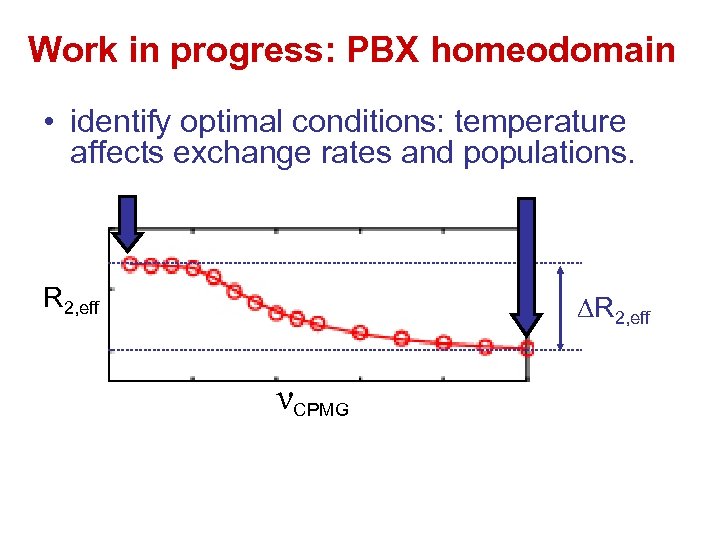Work in progress: PBX homeodomain • identify optimal conditions: temperature affects exchange rates and Work in progress: PBX homeodomain • identify optimal conditions: temperature affects exchange rates and populations. R 2, eff νCPMG

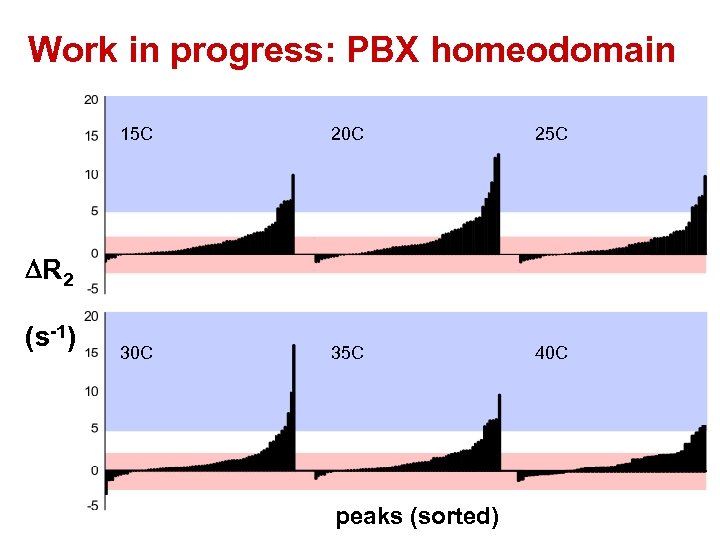Work in progress: PBX homeodomain 15 C 20 C 25 C 30 C 35 Work in progress: PBX homeodomain 15 C 20 C 25 C 30 C 35 C 40 C DR 2 (s-1) peaks (sorted)

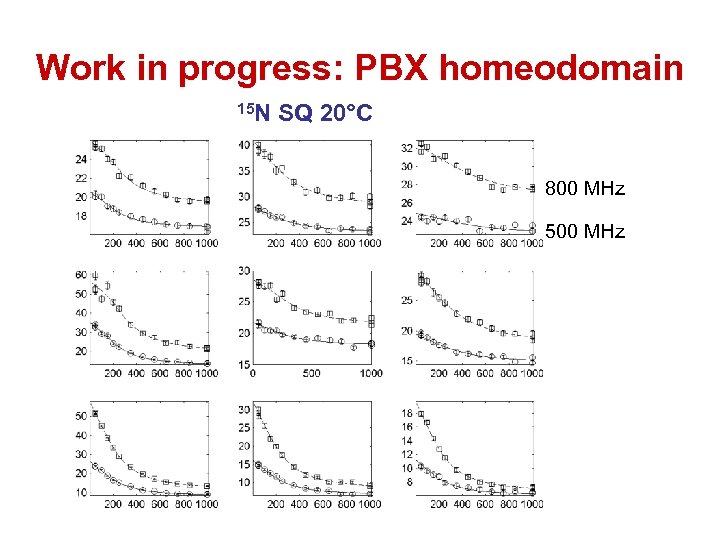Work in progress: PBX homeodomain 15 N SQ 20°C 800 MHz 500 MHz Work in progress: PBX homeodomain 15 N SQ 20°C 800 MHz 500 MHz

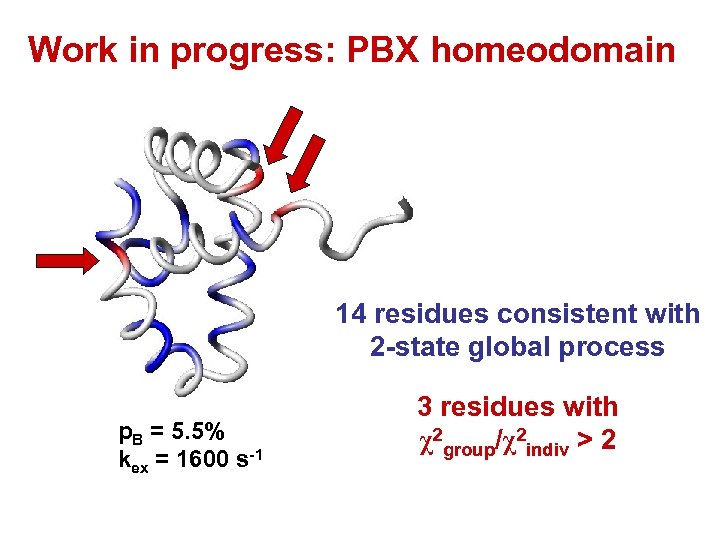Work in progress: PBX homeodomain 14 residues consistent with 2 -state global process p. Work in progress: PBX homeodomain 14 residues consistent with 2 -state global process p. B = 5. 5% kex = 1600 s-1 3 residues with χ2 group/χ2 indiv > 2

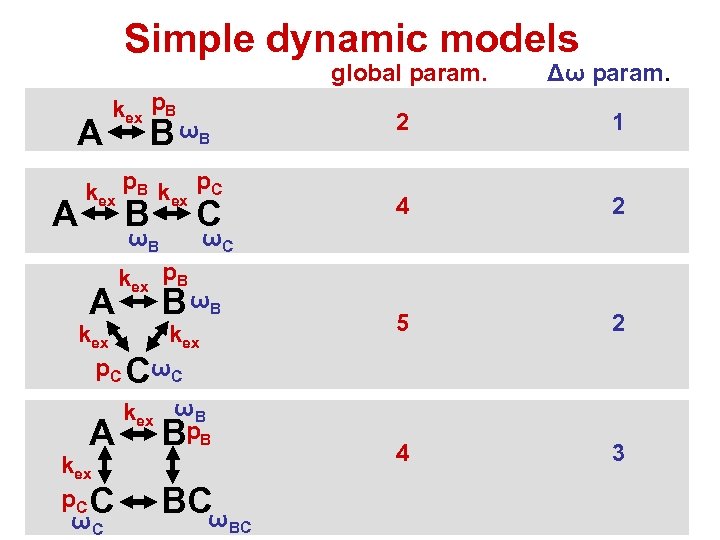Simple dynamic models global param. A A kex p. B 2 ωB A kex Simple dynamic models global param. A A kex p. B 2 ωB A kex p. C C ωC 3 ωC kex p. B B ωB kex p. C CωC A 2 4 C 2 5 kex p. B kex p. C 1 4 B ωB B Δω param. kex ωB Bp. B BCω BC