CHAPTER TWENTY-FOUR OPTIONS 1 TYPES OF OPTION

CHAPTER TWENTY-FOUR OPTIONS 1

TYPES OF OPTION CONTRACTS • WHAT IS AN OPTION? – Definition: a type of contract between two investors where one grants the other the right to buy or sell a specific asset in the future – the option buyer is buying the right to buy or sell the underlying asset at some future date – the option writer is selling the right to buy or sell the underlying asset at some future date 2

CALL OPTIONS • WHAT IS A CALL OPTION CONTRACT? – DEFINITION: a legal contract that specifies four conditions – FOUR CONDITIONS • the company whose shares can be bought • the number of shares that can be bought • the purchase price for the shares known as the exercise or strike price • the date when the right expires 3

CALL OPTIONS • Role of Exchange • exchanges created the Options Clearing Corporation (CCC) to facilitate trading a standardized contract (100 shares/contract) • OCC helps buyers and writers to “close out” a position 4

PUT OPTIONS • WHAT IS A PUT OPTION CONTRACT? – DEFINITION: a legal contract that specifies four conditions • the company whose shares can be sold • the number of shares that can be sold • the selling price for those shares known as the exercise or strike price • the date the right expires 5

OPTION TRADING • FEATURES OF OPTION TRADING – a new set of options is created every 3 months – new options expire in roughly 9 months – long term options (LEAPS) may expire in up to 2 years – some flexible options exist (FLEX) – once listed, the option remains until expiration date 6

OPTION TRADING • TRADING ACTIVITY – currently option trading takes place in the following locations: • • the Chicago Board Options Exchange (CBOS) the American Stock Exchange the Pacific Stock Exchange the Philadelphia Stock Exchange (especially currency options) 7

OPTION TRADING • THE MECHANICS OF EXCHANGE TRADING – Use of specialist – Use of market makers 8

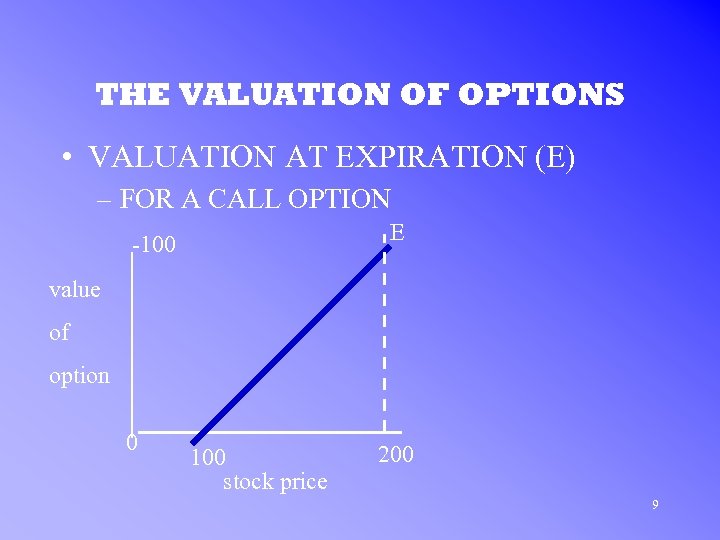THE VALUATION OF OPTIONS • VALUATION AT EXPIRATION (E) – FOR A CALL OPTION E -100 value of option 0 100 stock price 200 9

THE VALUATION OF OPTIONS • VALUATION AT EXPIRATION – ASSUME: the strike price = $100 – For a call if the stock price is less than $100, the option is worthless at expiration – The upward sloping line represents the intrinsic value of the option 10

THE VALUATION OF OPTIONS • VALUATION AT EXPIRATION – In equation form IVc = max {0, Ps, -E} where Ps is the price of the stock E is the exercise price 11

THE VALUATION OF OPTIONS • VALUATION AT EXPIRATION – ASSUME: the strike price = $100 – For a put if the stock price is greater than $100, the option is worthless at expiration – The downward sloping line represents the intrinsic value of the option 12

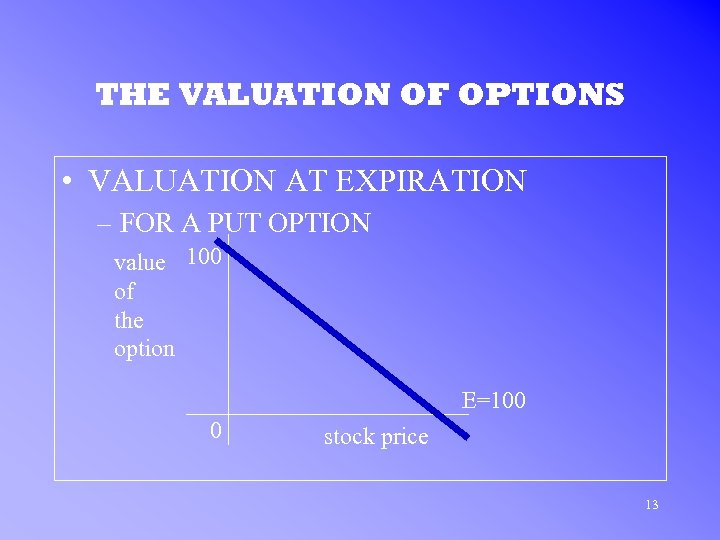THE VALUATION OF OPTIONS • VALUATION AT EXPIRATION – FOR A PUT OPTION value 100 of the option E=100 0 stock price 13

THE VALUATION OF OPTIONS • VALUATION AT EXPIRATION – FOR A CALL OPTION • if the strike price is greater than $100, the option is worthless at expiration 14

THE VALUATION OF OPTIONS – in equation form IVc = max {0, - Ps, E} where Ps is the price of the stock E is the exercise price 15

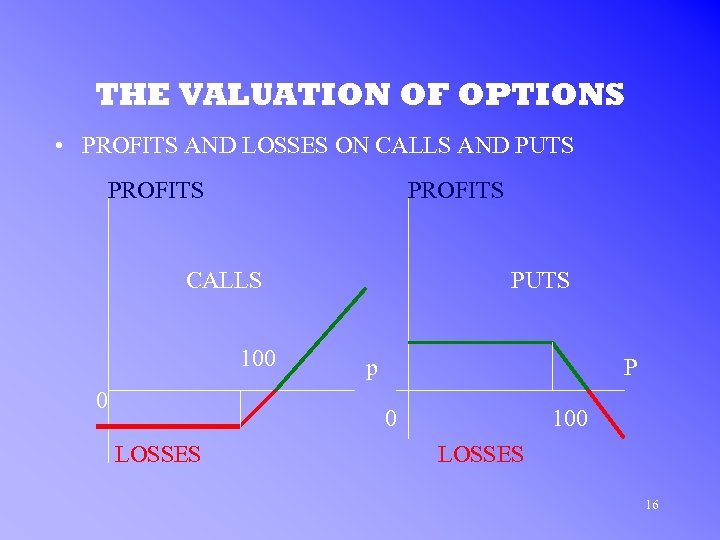THE VALUATION OF OPTIONS • PROFITS AND LOSSES ON CALLS AND PUTS PROFITS CALLS 100 0 PUTS p P 0 LOSSES 100 LOSSES 16

THE VALUATION OF OPTIONS • PROFITS AND LOSSES – Assume the underlying stock sells at $100 at time of initial transaction – Two kinked lines = the intrinsic value of the options 17

THE VALUATION OF OPTIONS • PROFIT EQUATIONS (CALLS) PC = IVC - PC = max {0, PS - E} - PC = max {-PC , PS - E - PC } This means that the kinked profit line for the call is the intrinsic value equation less the call premium (- PC ) 18

THE VALUATION OF OPTIONS • PROFIT EQUATIONS (CALLS) PP = IVP - PP = max {0, E - PS} - PP = max {-PP , E - PS - PP } This means that the kinked profit line for the put is the intrinsic value equation less the put premium (- PP ) 19

THE BINOMIAL OPTION PRICING MODEL (BOPM) • WHAT DOES BOPM DO? – it estimates the fair value of a call or a put option 20

THE BINOMIAL OPTION PRICING MODEL (BOPM) • TYPES OF OPTIONS – EUROPEAN is an option that can be exercised only on its expiration date – AMERICAN is an option that can be exercised any time up until and including its expiration date 21

THE BINOMIAL OPTION PRICING MODEL (BOPM) • EXAMPLE: CALL OPTIONS – ASSUMPTIONS: • • price of Widget stock = $100 at current t: t=0 after one year: t=T stock sells for either $125 (25% increase) $ 80 (20% decrease) 22

THE BINOMIAL OPTION PRICING MODEL (BOPM) • EXAMPLE: CALL OPTIONS – ASSUMPTIONS: • Annual riskfree rate = 8% compounded continuously • Investors cal lend or borrow through an 8% bond 23

THE BINOMIAL OPTION PRICING MODEL (BOPM) • Consider a call option on Widget Let the exercise price = $100 the exercise date = T and the exercise value: If Widget is at $125 = $25 or at $80 = 0 24

THE BINOMIAL OPTION PRICING MODEL (Price Tree) Annual Analysis: $125 P 0=25 $100 $80 Semiannual Analysis: $125 P 0=65 $111. 80 $100 P 0=0 $89. 44 $80 t=. 5 T P 0=$0 t=T P 0=0 25

THE BINOMIAL OPTION PRICING MODEL (BOPM) • VALUATION – What is a fair value for the call at time =0? • Two Possible Future States – The “Up State” when p = $125 – The “Down State” when p = $80 26

THE BINOMIAL OPTION PRICING MODEL (BOPM) • Summary Security Payoff: Up state Payoff: Down state Stock Bond Call $125. 00 108. 33 25. 00 $ 80. 00 108. 33 0. 00 Current Price $100. 00 ? ? ? 27

BOPM: REPLICATING PORTFOLIOS • REPLICATING PORTFOLIOS – The Widget call option can be replicated – Using an appropriate combination of • Widget Stock and • the 8% bond – The cost of replication equals the fair value of the option 28

BOPM: REPLICATING PORTFOLIOS • REPLICATING PORTFOLIOS – Why? • if otherwise, there would be an arbitrage opportunity – that is, the investor could buy the cheaper of the two alternatives and sell the more expensive one 29

BOPM: REPLICATING PORTFOLIOS – COMPOSITION OF THE REPLICATING PORTFOLIO: • Consider a portfolio with Ns shares of Widget • and Nb risk free bonds – In the up state • portfolio payoff = 125 Ns + 108. 33 Nb = $25 – In the down state 80 Ns + 108. 33 Nb = 0 30

BOPM: REPLICATING PORTFOLIOS – COMPOSITION OF THE REPLICATING PORTFOLIO: • Solving the two equations simultaneously (125 -80)Ns = $25 Ns =. 5556 Substituting in either equation yields Nb = -. 4103 31

BOPM: REPLICATING PORTFOLIOS • INTERPRETATION – Investor replicates payoffs from the call by • Short selling the bonds: $41. 03 • Purchasing. 5556 shares of Widget 32

BOPM: REPLICATING PORTFOLIOS Portfolio Component Stock Loan Net Payoff In Up State. 5556 x $125 = $6 9. 45 -$41. 03 x 1. 0833 = -$44. 45 $25. 00 Payoff In Down State. 5556 x $80 = $ 44. 45 -$41. 03 x 1. 0833 = -$ 44. 45 $0. 00 33

BOPM: REPLICATING PORTFOLIOS • TO OBTAIN THE PORTFOLIO – $55. 56 must be spent to purchase. 5556 shares at $100 per share – but $41. 03 income is provided by the bonds such that $55. 56 - 41. 03 = $14. 53 34

BOPM: REPLICATING PORTFOLIOS • MORE GENERALLY where V 0 Pd Pb Nd Nb = the value of the option = the stock price = the risk free bond price = the number of shares = the number of bonds 35

THE HEDGE RATIO • THE HEDGE RATIO – DEFINITION: the expected change in the value of an option per dollar change in the market price of an underlying asset – The price of the call should change by $. 5556 for every $1 change in stock price 36

THE HEDGE RATIO • THE HEDGE RATIO where P = the end-of-period price o = the option s = the stock u = up d = down 37

THE HEDGE RATIO • THE HEDGE RATIO – to replicate a call option • h shares must be purchased • B is the amount borrowed by short selling bonds B = PV(h Psd - Pod ) 38

THE HEDGE RATIO – the value of a call option V 0 = h P s - B where h = B= the hedge ratio the current value of a short bond position in a portfolio that replicates the payoffs of the call 39

PUT-CALL PARITY • Relationship of hedge ratios: hp = hc - 1 where hp = the hedge ratio of a call hc = the hedge ratio of a put 40

PUT-CALL PARITY – DEFINITION: the relationship between the market price of a put and a call that have the same exercise price, expiration date, and underlying stock 41

PUT-CALL PARITY • FORMULA: PP + PS = PC + E / e. RT where PP and PC denote the current market prices of the put and the call 42

THE BLACK-SCHOLES MODEL • What if the number of periods before expiration were allowed to increase infinitely? 43

THE BLACK-SCHOLES MODEL • The Black-Scholes formula for valuing a call option where 44

THE BLACK-SCHOLES MODEL and where Ps = the stock’s current market price E = the exercise price R = continuously compounded risk free rate T = the time remaining to expire s = risk (standard deviation of the stock’s annual return) 45

THE BLACK-SCHOLES MODEL • NOTES: – E/e. RT = the PV of the exercise price where continuous discount rate is used – N(d 1 ), N(d 2 )= the probabilities that outcomes of less will occur in a normal distribution with mean = 0 and s = 1 46

THE BLACK-SCHOLES MODEL • What happens to the fair value of an option when one input is changed while holding the other four constant? – The higher the stock price, the higher the option’s value – The higher the exercise price, the lower the option’s value – The longer the time to expiration, the higher the option’s value 47

THE BLACK-SCHOLES MODEL • What happens to the fair value of an option when one input is changed while holding the other four constant? – The higher the risk free rate, the higher the option’s value – The greater the risk, the higher the option’s value 48

THE BLACK-SCHOLES MODEL • LIMITATIONS OF B/S MODEL: – It only applies to • European-style options • stocks that pay NO dividends 49