Varian_Chapter04_Utility_mod.ppt
- Количество слайдов: 87
 Chapter Four Utility
Chapter Four Utility
 Preferences - A Reminder p ux y: x is preferred strictly to y. u x ~ y: x and y are equally preferred. u x f y: x is preferred at least as ~ much as is y.
Preferences - A Reminder p ux y: x is preferred strictly to y. u x ~ y: x and y are equally preferred. u x f y: x is preferred at least as ~ much as is y.
 Preferences - A Reminder u Completeness: For any two bundles x and y it is always possible to state either that x f y ~ or that y f x. ~
Preferences - A Reminder u Completeness: For any two bundles x and y it is always possible to state either that x f y ~ or that y f x. ~
 Preferences - A Reminder u Reflexivity: Any bundle x is always at least as preferred as itself; i. e. x f ~ x.
Preferences - A Reminder u Reflexivity: Any bundle x is always at least as preferred as itself; i. e. x f ~ x.
 Preferences - A Reminder u Transitivity: If x is at least as preferred as y, and y is at least as preferred as z, then x is at least as preferred as z; i. e. x f ~ y and y fz ~ x f ~ z.
Preferences - A Reminder u Transitivity: If x is at least as preferred as y, and y is at least as preferred as z, then x is at least as preferred as z; i. e. x f ~ y and y fz ~ x f ~ z.
 Utility u Now we talk about consumer preferences and utility is only a way to describe preferences u All economists have to know is which bundles has a higher utility, how much higher does not matter at all
Utility u Now we talk about consumer preferences and utility is only a way to describe preferences u All economists have to know is which bundles has a higher utility, how much higher does not matter at all
 Utility u How to measure person’s overall well-being u Utility was thought of as a numeric measure of a person’s happines. u Does it makes sense? u Can one compare utility?
Utility u How to measure person’s overall well-being u Utility was thought of as a numeric measure of a person’s happines. u Does it makes sense? u Can one compare utility?
 Utility Functions u A utility function is a way of assigning a number to every possible consumption bundle such that moreprefered budles get assigned larger number than less-preffered bundles.
Utility Functions u A utility function is a way of assigning a number to every possible consumption bundle such that moreprefered budles get assigned larger number than less-preffered bundles.
 Utility Functions u. A preference relation that is complete, reflexive, transitive and continuous can be represented by a continuous utility function. u Continuity means that small changes to a consumption bundle cause only small changes to the preference level.
Utility Functions u. A preference relation that is complete, reflexive, transitive and continuous can be represented by a continuous utility function. u Continuity means that small changes to a consumption bundle cause only small changes to the preference level.
 Utility Functions u. A utility function U(x) represents a preference relation f if and only if: ~ p x’ x” U(x’) > U(x”) x’ p x” U(x’) < U(x”) x’ ~ x” U(x’) = U(x”).
Utility Functions u. A utility function U(x) represents a preference relation f if and only if: ~ p x’ x” U(x’) > U(x”) x’ p x” U(x’) < U(x”) x’ ~ x” U(x’) = U(x”).
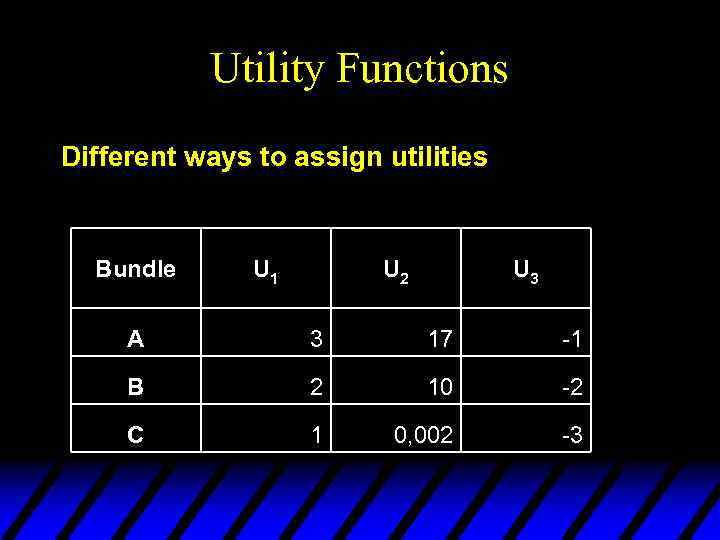 Utility Functions Different ways to assign utilities Bundle U 1 U 2 U 3 A 3 17 -1 B 2 10 -2 C 1 0, 002 -3
Utility Functions Different ways to assign utilities Bundle U 1 U 2 U 3 A 3 17 -1 B 2 10 -2 C 1 0, 002 -3
 Utility Functions Ordinal utility vs. cardinal utility Does „twice as” make any sense?
Utility Functions Ordinal utility vs. cardinal utility Does „twice as” make any sense?
 Utility Functions & Indiff. Curves u Consider the bundles (4, 1), (2, 3) and (2, 2). u Suppose (2, 3) (4, 1) ~ (2, 2). u Assign to these bundles any numbers that preserve the preference ordering; e. g. U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4. u Call these numbers utility levels. p
Utility Functions & Indiff. Curves u Consider the bundles (4, 1), (2, 3) and (2, 2). u Suppose (2, 3) (4, 1) ~ (2, 2). u Assign to these bundles any numbers that preserve the preference ordering; e. g. U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4. u Call these numbers utility levels. p
 Utility Functions & Indiff. Curves u An indifference curve contains equally preferred bundles. preference same utility level. u Therefore, all bundles in an indifference curve have the same utility level. u Equal
Utility Functions & Indiff. Curves u An indifference curve contains equally preferred bundles. preference same utility level. u Therefore, all bundles in an indifference curve have the same utility level. u Equal
 Utility Functions & Indiff. Curves u So the bundles (4, 1) and (2, 2) are in the indiff. curve with utility level U 4 u But the bundle (2, 3) is in the indiff. curve with utility level U 6. u On an indifference curve diagram, this preference information looks as follows:
Utility Functions & Indiff. Curves u So the bundles (4, 1) and (2, 2) are in the indiff. curve with utility level U 4 u But the bundle (2, 3) is in the indiff. curve with utility level U 6. u On an indifference curve diagram, this preference information looks as follows:
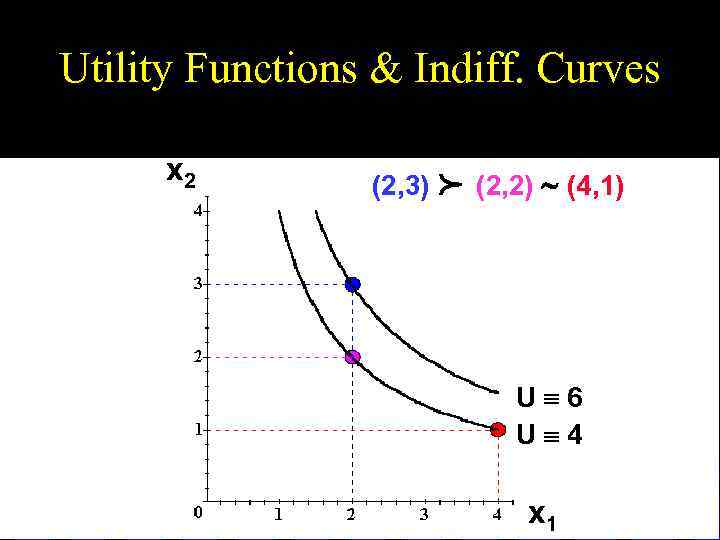 Utility Functions & Indiff. Curves (2, 3) p x 2 (2, 2) ~ (4, 1) U 6 U 4 x 1
Utility Functions & Indiff. Curves (2, 3) p x 2 (2, 2) ~ (4, 1) U 6 U 4 x 1
 Utility Functions & Indiff. Curves u Another way to visualize this same information is to plot the utility level on a vertical axis.
Utility Functions & Indiff. Curves u Another way to visualize this same information is to plot the utility level on a vertical axis.
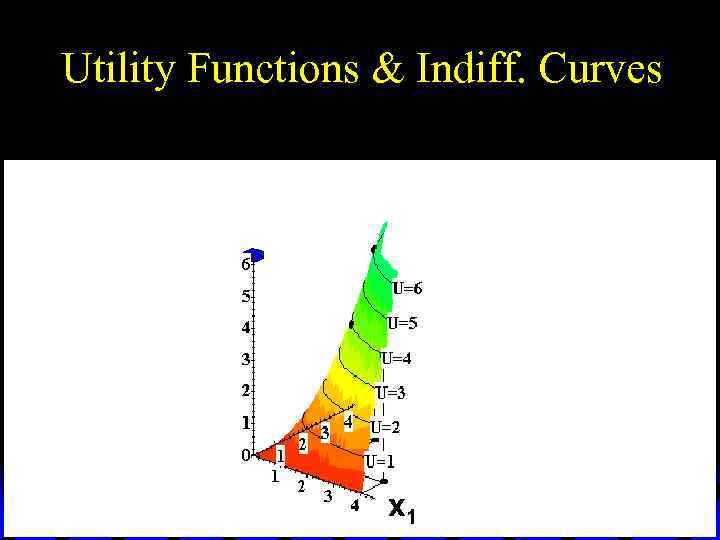
 Utility Functions & Indiff. Curves 3 D plot of consumption & utility levels for 3 bundles U(2, 3) = 6 Utility U(2, 2) = 4 U(4, 1) = 4 x 2 x 1
Utility Functions & Indiff. Curves 3 D plot of consumption & utility levels for 3 bundles U(2, 3) = 6 Utility U(2, 2) = 4 U(4, 1) = 4 x 2 x 1
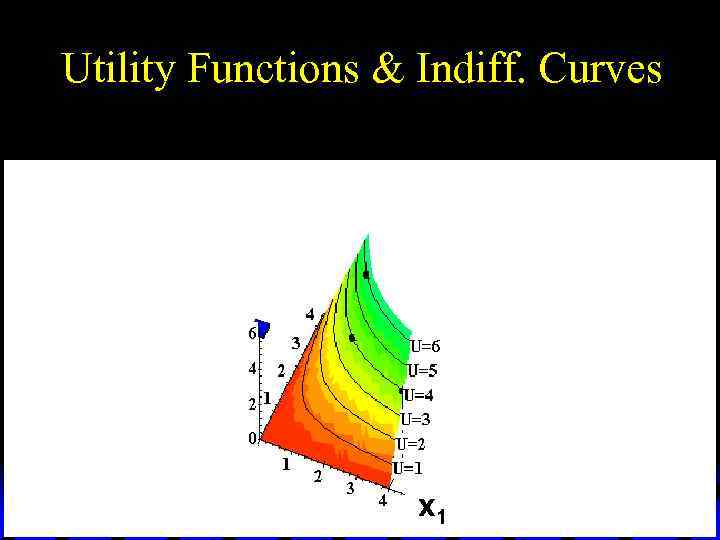
 Utility Functions & Indiff. Curves u This 3 D visualization of preferences can be made more informative by adding into it the two indifference curves.
Utility Functions & Indiff. Curves u This 3 D visualization of preferences can be made more informative by adding into it the two indifference curves.
 Utility Functions & Indiff. Curves Utility U 6 U 4 x 2 x 1 Higher indifference curves contain more preferred bundles.
Utility Functions & Indiff. Curves Utility U 6 U 4 x 2 x 1 Higher indifference curves contain more preferred bundles.
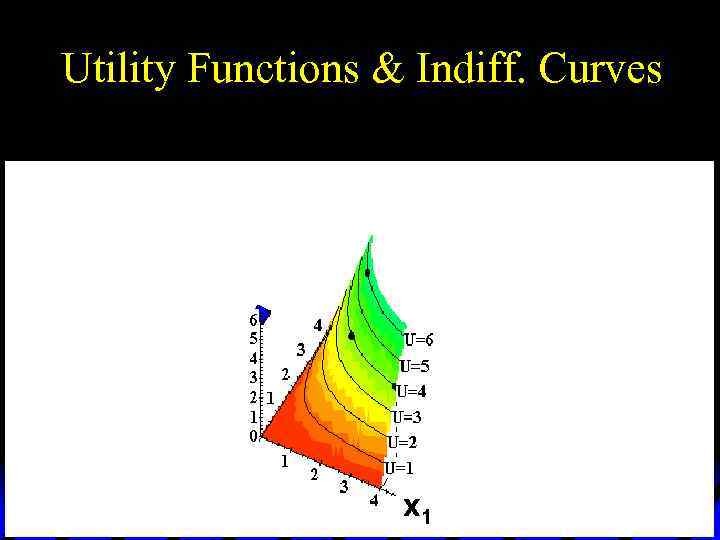
 Utility Functions & Indiff. Curves u Comparing more bundles will create a larger collection of all indifference curves and a better description of the consumer’s preferences.
Utility Functions & Indiff. Curves u Comparing more bundles will create a larger collection of all indifference curves and a better description of the consumer’s preferences.
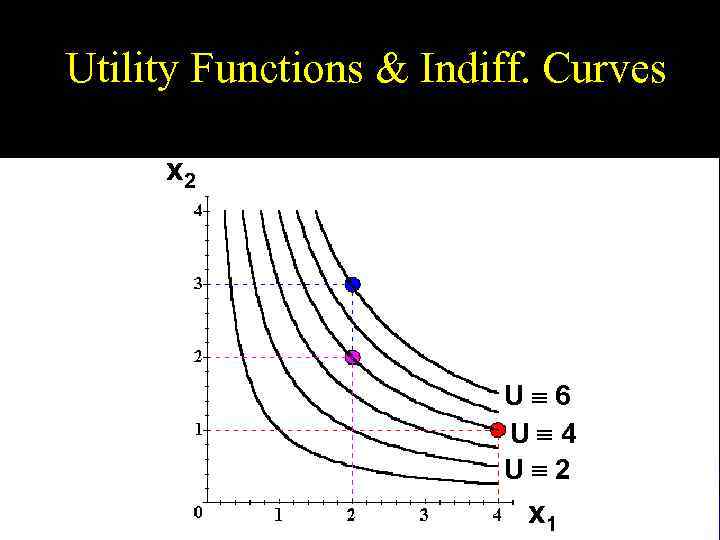 Utility Functions & Indiff. Curves x 2 U 6 U 4 U 2 x 1
Utility Functions & Indiff. Curves x 2 U 6 U 4 U 2 x 1
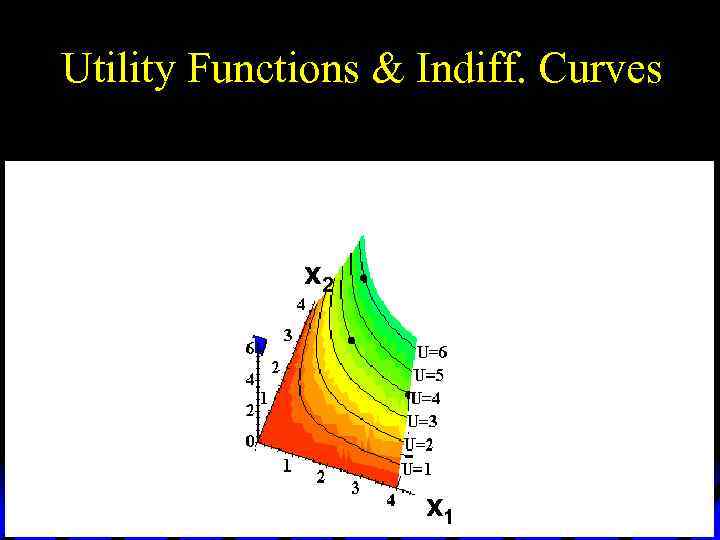
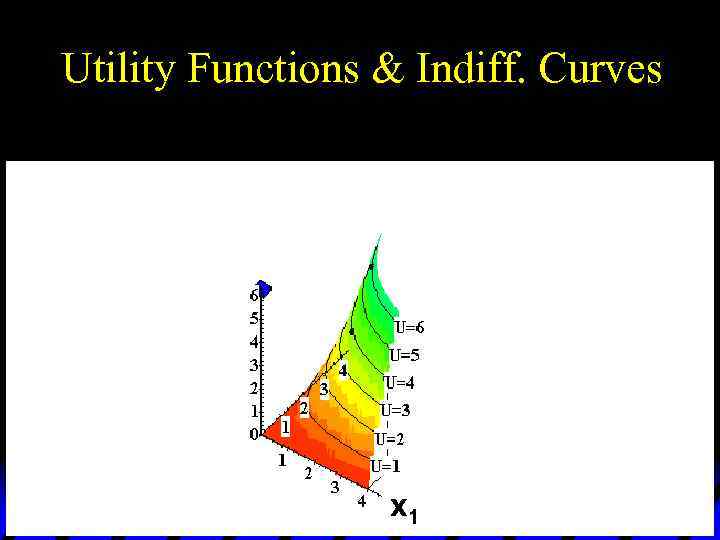
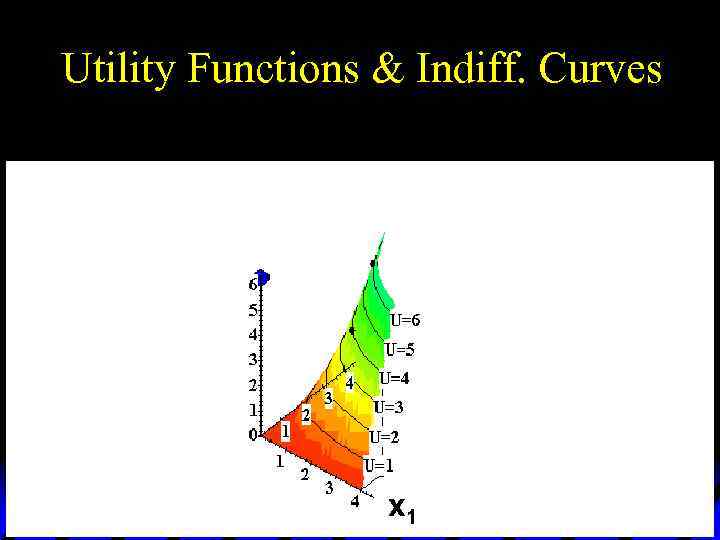
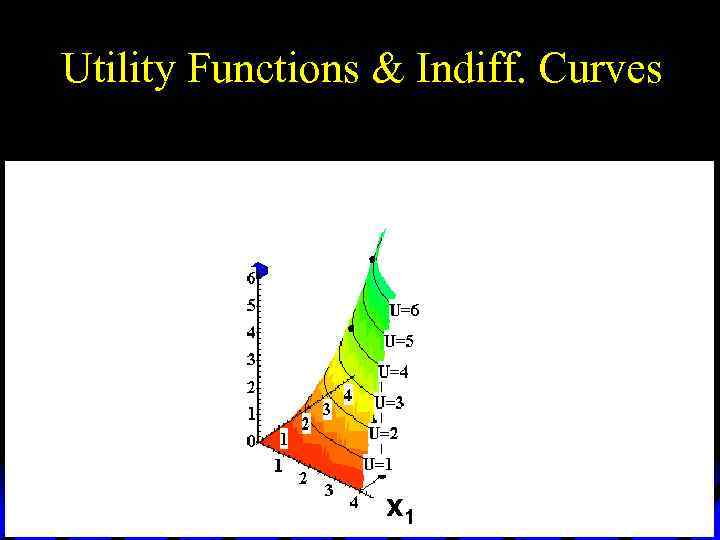
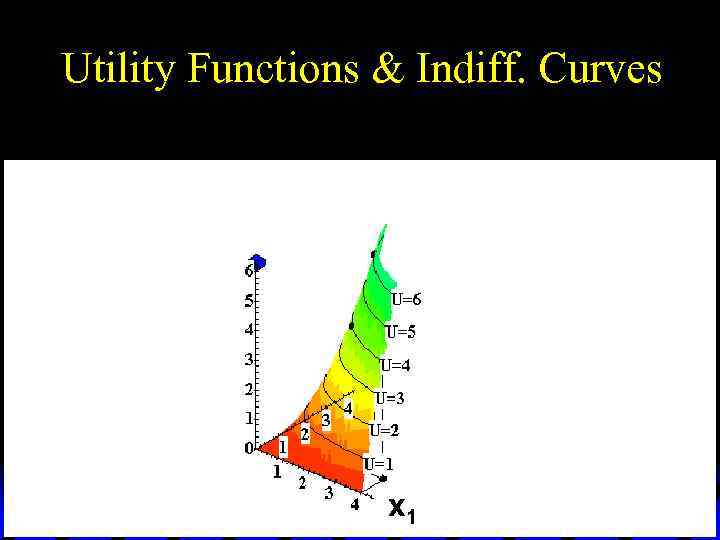
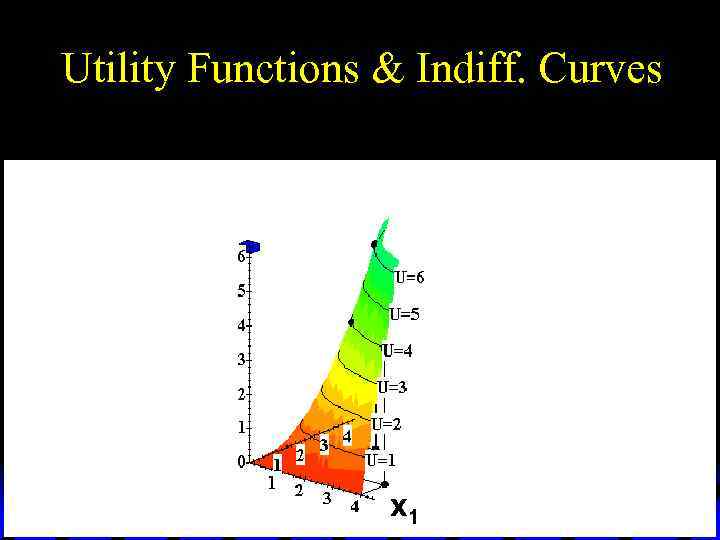
 Utility Functions & Indiff. Curves u As before, this can be visualized in 3 D by plotting each indifference curve at the height of its utility index.
Utility Functions & Indiff. Curves u As before, this can be visualized in 3 D by plotting each indifference curve at the height of its utility index.
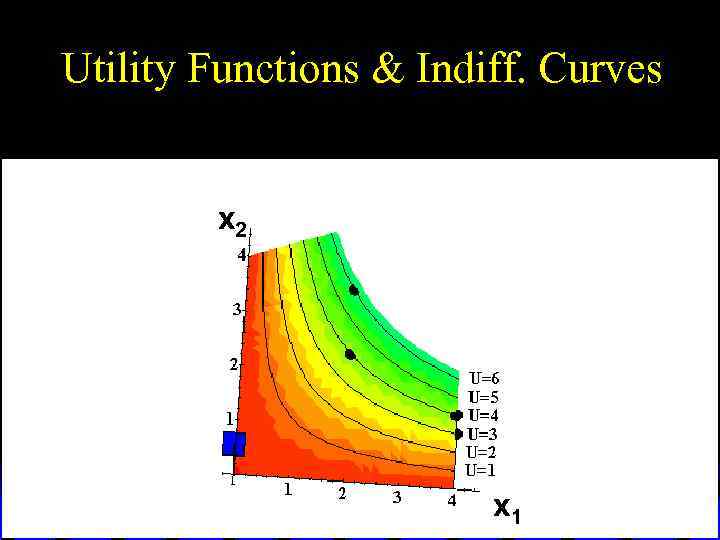
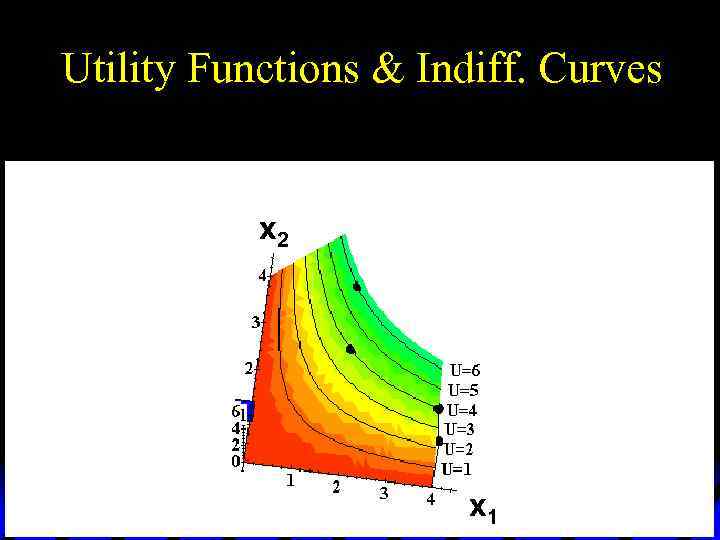
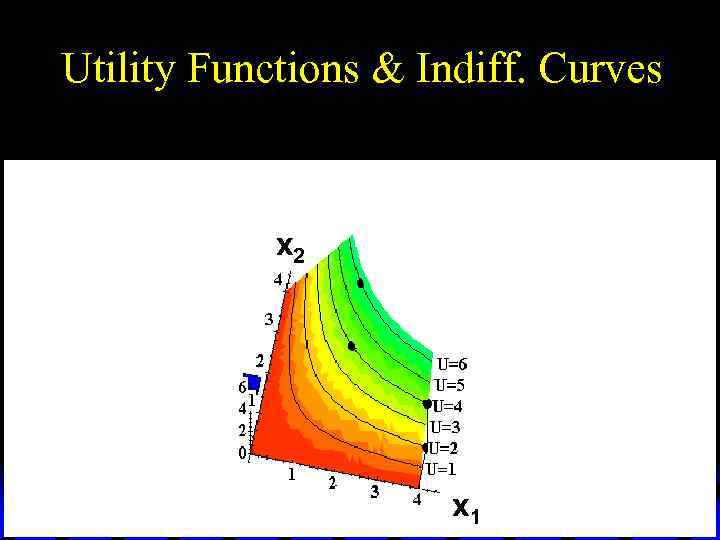
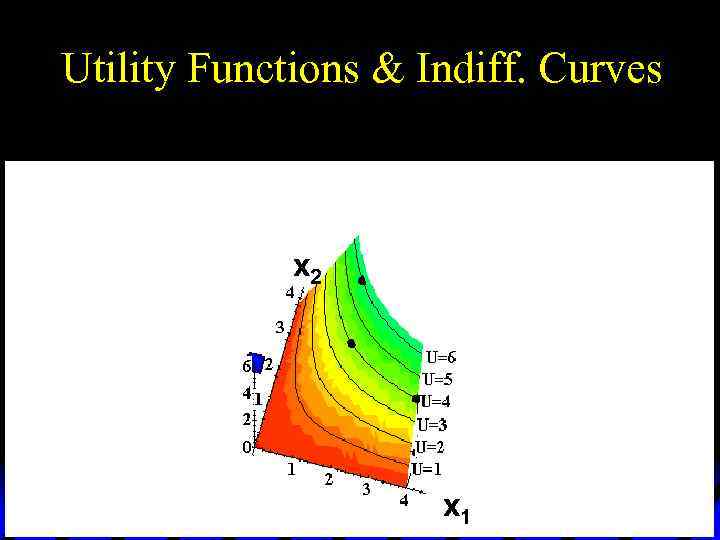
 Utility Functions & Indiff. Curves Utility U 6 U 5 U 4 U 3 U 2 x 2 U 1 x 1
Utility Functions & Indiff. Curves Utility U 6 U 5 U 4 U 3 U 2 x 2 U 1 x 1
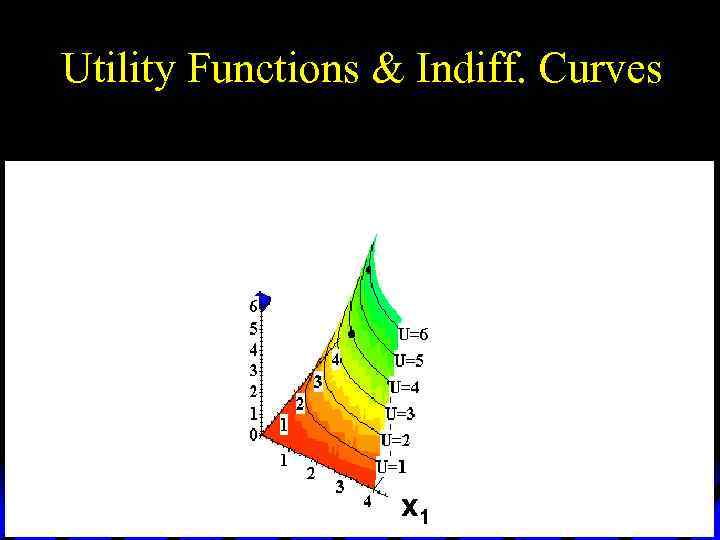
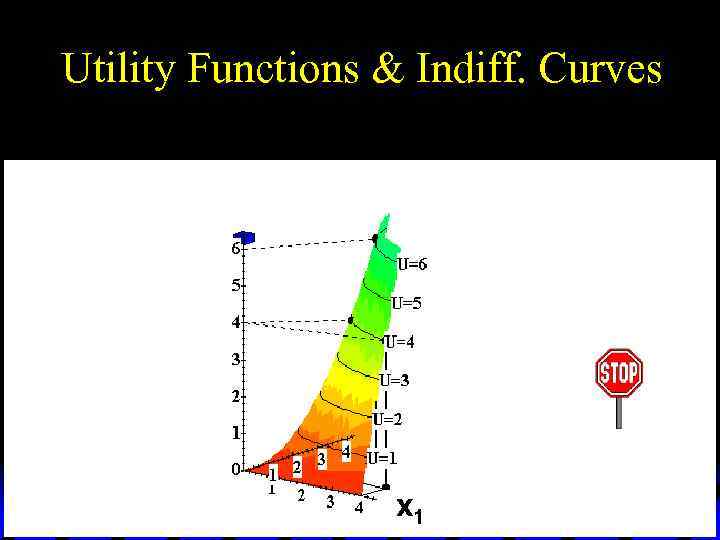
 Utility Functions & Indiff. Curves u Comparing all possible consumption bundles gives the complete collection of the consumer’s indifference curves, each with its assigned utility level. u This complete collection of indifference curves completely represents the consumer’s preferences.
Utility Functions & Indiff. Curves u Comparing all possible consumption bundles gives the complete collection of the consumer’s indifference curves, each with its assigned utility level. u This complete collection of indifference curves completely represents the consumer’s preferences.
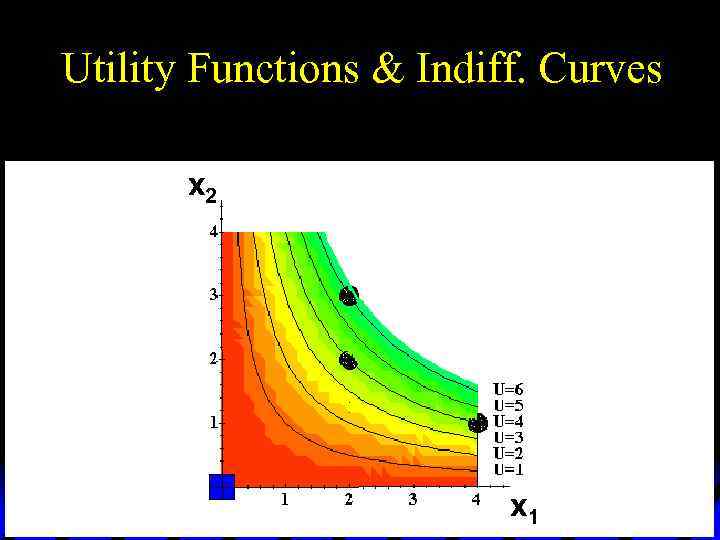 Utility Functions & Indiff. Curves x 2 x 1
Utility Functions & Indiff. Curves x 2 x 1
 Utility Functions & Indiff. Curves x 2 x 1
Utility Functions & Indiff. Curves x 2 x 1
 Utility Functions & Indiff. Curves x 2 x 1
Utility Functions & Indiff. Curves x 2 x 1
 Utility Functions & Indiff. Curves x 2 x 1
Utility Functions & Indiff. Curves x 2 x 1
 Utility Functions & Indiff. Curves x 2 x 1
Utility Functions & Indiff. Curves x 2 x 1
 Utility Functions & Indiff. Curves x 2 x 1
Utility Functions & Indiff. Curves x 2 x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves x 1
Utility Functions & Indiff. Curves x 1
 Utility Functions & Indiff. Curves u The collection of all indifference curves for a given preference relation is an indifference map. u An indifference map is equivalent to a utility function; each is the other.
Utility Functions & Indiff. Curves u The collection of all indifference curves for a given preference relation is an indifference map. u An indifference map is equivalent to a utility function; each is the other.
 Utility Functions u There is no unique utility function representation of a preference relation. u Suppose U(x 1, x 2) = x 1 x 2 represents a preference relation. u Again consider the bundles (4, 1), (2, 3) and (2, 2).
Utility Functions u There is no unique utility function representation of a preference relation. u Suppose U(x 1, x 2) = x 1 x 2 represents a preference relation. u Again consider the bundles (4, 1), (2, 3) and (2, 2).
 Utility Functions u U(x 1, x 2) = x 1 x 2, so U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4; p that is, (2, 3) (4, 1) ~ (2, 2).
Utility Functions u U(x 1, x 2) = x 1 x 2, so U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4; p that is, (2, 3) (4, 1) ~ (2, 2).
 Utility Functions = x 1 x 2 u Define V = U 2. (2, 3) p u U(x 1, x 2) (4, 1) ~ (2, 2).
Utility Functions = x 1 x 2 u Define V = U 2. (2, 3) p u U(x 1, x 2) (4, 1) ~ (2, 2).
 Utility Functions p = x 1 x 2 (2, 3) (4, 1) ~ (2, 2). u Define V = U 2. u Then V(x 1, x 2) = x 12 x 22 and V(2, 3) = 36 > V(4, 1) = V(2, 2) = 16 so again (2, 3) (4, 1) ~ (2, 2). u V preserves the same order as U and so represents the same preferences. u U(x 1, x 2) p
Utility Functions p = x 1 x 2 (2, 3) (4, 1) ~ (2, 2). u Define V = U 2. u Then V(x 1, x 2) = x 12 x 22 and V(2, 3) = 36 > V(4, 1) = V(2, 2) = 16 so again (2, 3) (4, 1) ~ (2, 2). u V preserves the same order as U and so represents the same preferences. u U(x 1, x 2) p
 Utility Functions = x 1 x 2 (2, 3) u Define W = 2 U + 10. p u U(x 1, x 2) (4, 1) ~ (2, 2).
Utility Functions = x 1 x 2 (2, 3) u Define W = 2 U + 10. p u U(x 1, x 2) (4, 1) ~ (2, 2).
 Utility Functions p = x 1 x 2 (2, 3) (4, 1) ~ (2, 2). u Define W = 2 U + 10. u Then W(x 1, x 2) = 2 x 1 x 2+10 so W(2, 3) = 22 > W(4, 1) = W(2, 2) = 18. Again, (2, 3) (4, 1) ~ (2, 2). u W preserves the same order as U and V and so represents the same preferences. u U(x 1, x 2) p
Utility Functions p = x 1 x 2 (2, 3) (4, 1) ~ (2, 2). u Define W = 2 U + 10. u Then W(x 1, x 2) = 2 x 1 x 2+10 so W(2, 3) = 22 > W(4, 1) = W(2, 2) = 18. Again, (2, 3) (4, 1) ~ (2, 2). u W preserves the same order as U and V and so represents the same preferences. u U(x 1, x 2) p
 Utility Functions u If – U is a utility function that represents a preference relation f ~ and – f is a strictly increasing function, u then V = f(U) is also a utility function representing f. ~ u This is monotonic transformation
Utility Functions u If – U is a utility function that represents a preference relation f ~ and – f is a strictly increasing function, u then V = f(U) is also a utility function representing f. ~ u This is monotonic transformation
 Utility Functions u Monotonic transformation of a utility function is a utility function that represents the same preferences as a original utility function.
Utility Functions u Monotonic transformation of a utility function is a utility function that represents the same preferences as a original utility function.
 Goods, Bads and Neutrals u. A good is a commodity unit which increases utility (gives a more preferred bundle). u A bad is a commodity unit which decreases utility (gives a less preferred bundle). u A neutral is a commodity unit which does not change utility (gives an equally preferred bundle).
Goods, Bads and Neutrals u. A good is a commodity unit which increases utility (gives a more preferred bundle). u A bad is a commodity unit which decreases utility (gives a less preferred bundle). u A neutral is a commodity unit which does not change utility (gives an equally preferred bundle).
 Goods, Bads and Neutrals Utility Units of water are goods x’ Utility function Units of water are bads Water Around x’ units, a little extra water is a neutral.
Goods, Bads and Neutrals Utility Units of water are goods x’ Utility function Units of water are bads Water Around x’ units, a little extra water is a neutral.
 Some Other Utility Functions and Their Indifference Curves u Perfect substitues How will the utility function look like?
Some Other Utility Functions and Their Indifference Curves u Perfect substitues How will the utility function look like?
 Some Other Utility Functions and Their Indifference Curves u V(x 1, x 2) = x 1 + x 2. What do the indifference curves for this “perfect substitution” utility function look like?
Some Other Utility Functions and Their Indifference Curves u V(x 1, x 2) = x 1 + x 2. What do the indifference curves for this “perfect substitution” utility function look like?
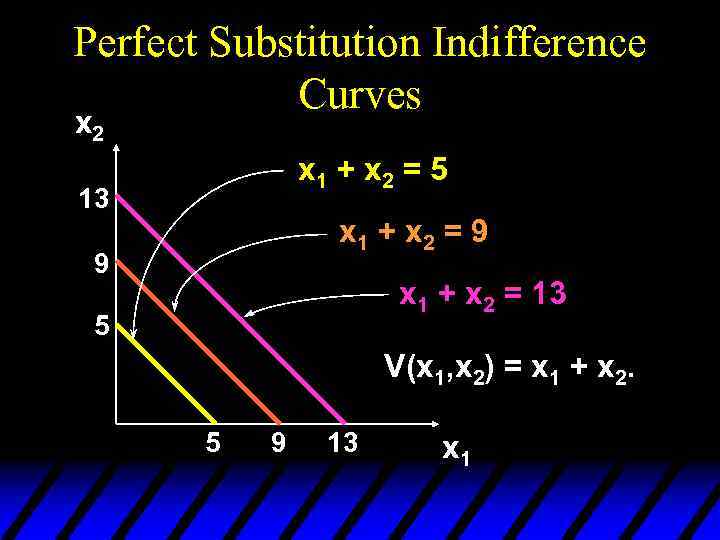 Perfect Substitution Indifference Curves x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2. 5 9 13 x 1
Perfect Substitution Indifference Curves x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2. 5 9 13 x 1
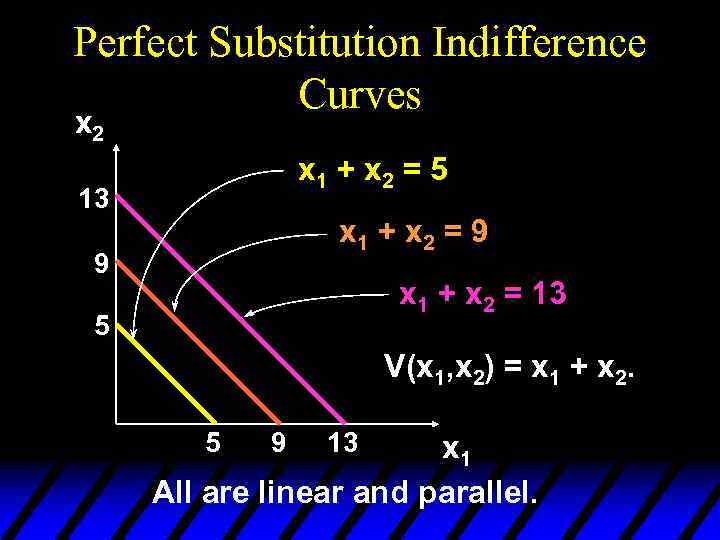 Perfect Substitution Indifference Curves x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2. 5 9 13 x 1 All are linear and parallel.
Perfect Substitution Indifference Curves x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2. 5 9 13 x 1 All are linear and parallel.
 Some Other Utility Functions and Their Indifference Curves u Is V(x 1, x 2) = x 1 + x 2 the only utility function for perfect substitues? What about square of x 1 and x 2 ? What about twice of x 1 and x 2 ? What if the ratio is not 1: 1?
Some Other Utility Functions and Their Indifference Curves u Is V(x 1, x 2) = x 1 + x 2 the only utility function for perfect substitues? What about square of x 1 and x 2 ? What about twice of x 1 and x 2 ? What if the ratio is not 1: 1?
 Some Other Utility Functions and Their Indifference Curves u Perfect complements How will the utility function look like?
Some Other Utility Functions and Their Indifference Curves u Perfect complements How will the utility function look like?
 Some Other Utility Functions and Their Indifference Curves u Instead of U(x 1, x 2) = x 1 x 2 or V(x 1, x 2) = x 1 + x 2, consider W(x 1, x 2) = min{x 1, x 2}. What do the indifference curves for this “perfect complementarity” utility function look like?
Some Other Utility Functions and Their Indifference Curves u Instead of U(x 1, x 2) = x 1 x 2 or V(x 1, x 2) = x 1 + x 2, consider W(x 1, x 2) = min{x 1, x 2}. What do the indifference curves for this “perfect complementarity” utility function look like?
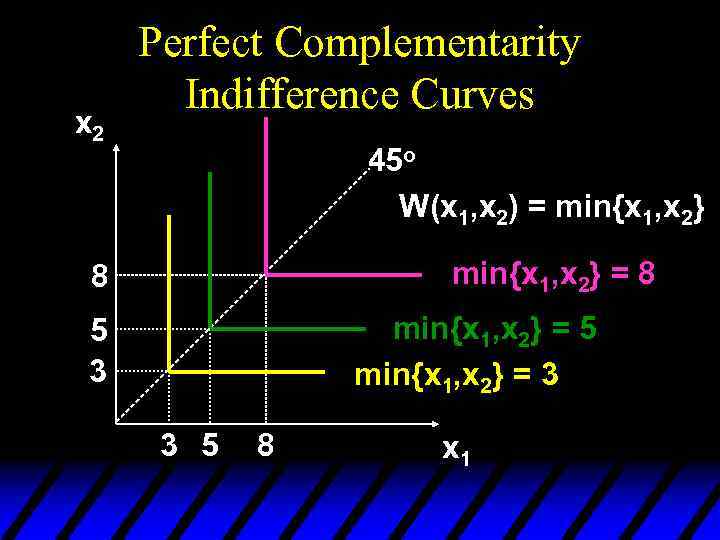 x 2 Perfect Complementarity Indifference Curves 45 o W(x 1, x 2) = min{x 1, x 2} = 8 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 5 3 3 5 8 x 1
x 2 Perfect Complementarity Indifference Curves 45 o W(x 1, x 2) = min{x 1, x 2} = 8 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 5 3 3 5 8 x 1
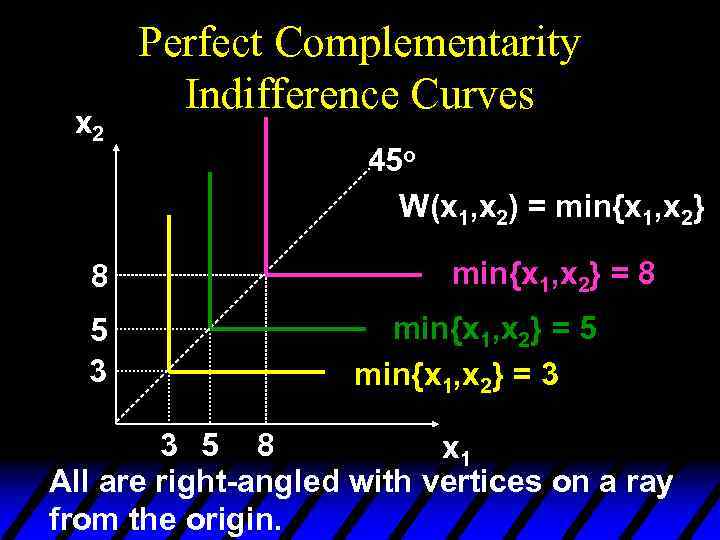 x 2 8 5 3 Perfect Complementarity Indifference Curves 45 o W(x 1, x 2) = min{x 1, x 2} = 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 3 5 8 x 1 All are right-angled with vertices on a ray from the origin.
x 2 8 5 3 Perfect Complementarity Indifference Curves 45 o W(x 1, x 2) = min{x 1, x 2} = 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 3 5 8 x 1 All are right-angled with vertices on a ray from the origin.
 Some Other Utility Functions and Their Indifference Curves u W(x 1, x 2) = min{x 1, x 2}. What is the ratio is not 1: 1? Two teaspoons od sugar per cup of tea? If x 1 is number of cups, then W(x 1, x 2) = min{x 1, 1/2 x 2}? or W(x 1, x 2) = min{x 1, 2 x 2}?
Some Other Utility Functions and Their Indifference Curves u W(x 1, x 2) = min{x 1, x 2}. What is the ratio is not 1: 1? Two teaspoons od sugar per cup of tea? If x 1 is number of cups, then W(x 1, x 2) = min{x 1, 1/2 x 2}? or W(x 1, x 2) = min{x 1, 2 x 2}?
 Some Other Utility Functions and Their Indifference Curves u. A utility function of the form U(x 1, x 2) = f(x 1) + x 2 is linear in just x 2 and is called quasilinear. u E. g. U(x 1, x 2) = 2 x 11/2 + x 2.
Some Other Utility Functions and Their Indifference Curves u. A utility function of the form U(x 1, x 2) = f(x 1) + x 2 is linear in just x 2 and is called quasilinear. u E. g. U(x 1, x 2) = 2 x 11/2 + x 2.
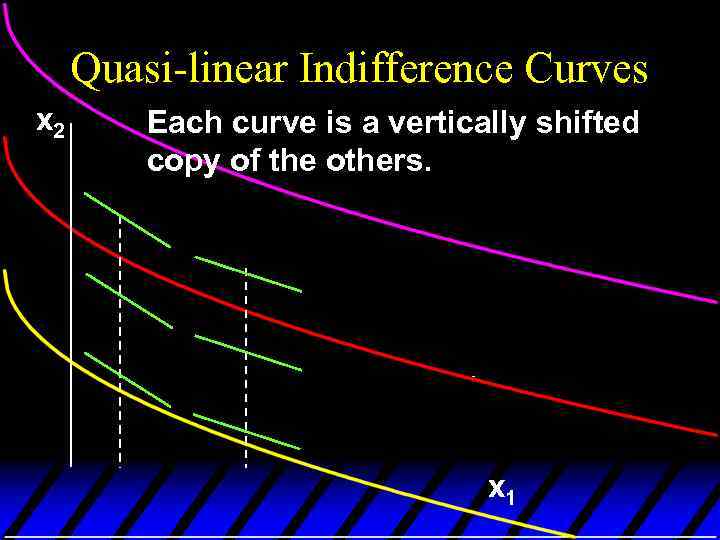 Quasi-linear Indifference Curves x 2 Each curve is a vertically shifted copy of the others. x 1
Quasi-linear Indifference Curves x 2 Each curve is a vertically shifted copy of the others. x 1
 Some Other Utility Functions and Their Indifference Curves u Any utility function of the form U(x 1, x 2) = x 1 a x 2 b with a > 0 and b > 0 is called a Cobb. Douglas utility function. u E. g. U(x 1, x 2) = x 11/2 x 21/2 (a = b = 1/2) V(x 1, x 2) = x 1 x 23 (a = 1, b = 3)
Some Other Utility Functions and Their Indifference Curves u Any utility function of the form U(x 1, x 2) = x 1 a x 2 b with a > 0 and b > 0 is called a Cobb. Douglas utility function. u E. g. U(x 1, x 2) = x 11/2 x 21/2 (a = b = 1/2) V(x 1, x 2) = x 1 x 23 (a = 1, b = 3)
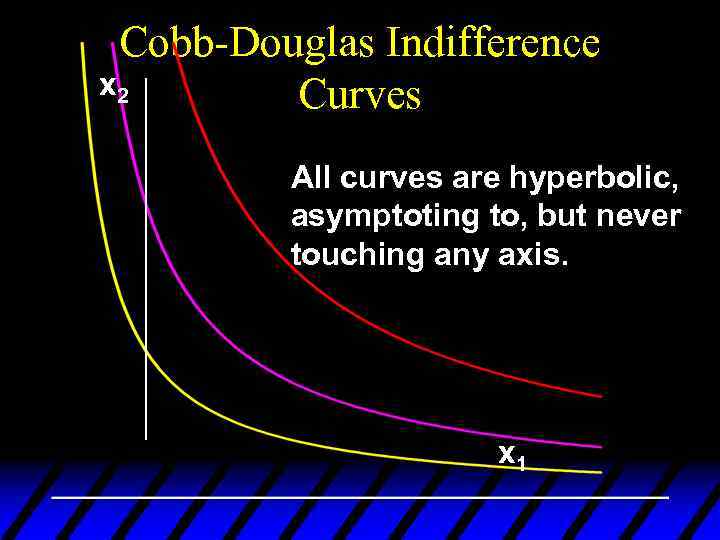 Cobb-Douglas Indifference x 2 Curves All curves are hyperbolic, asymptoting to, but never touching any axis. x 1
Cobb-Douglas Indifference x 2 Curves All curves are hyperbolic, asymptoting to, but never touching any axis. x 1
 Some Other Utility Functions and Their Indifference Curves u Cobb-Douglas utility function U(x 1, x 2) = x 1 b x 2 c can be expressed as: U(x 1, x 2) = x 1 a x 21 -a Proof….
Some Other Utility Functions and Their Indifference Curves u Cobb-Douglas utility function U(x 1, x 2) = x 1 b x 2 c can be expressed as: U(x 1, x 2) = x 1 a x 21 -a Proof….
 Some Other Utility Functions and Their Indifference Curves u Cobb-Douglas utility function U(x 1, x 2) = x 1 a x 2 b Monotonic transformations: - natural logarithm - sum of exponents is 1
Some Other Utility Functions and Their Indifference Curves u Cobb-Douglas utility function U(x 1, x 2) = x 1 a x 2 b Monotonic transformations: - natural logarithm - sum of exponents is 1
 Marginal Utilities u Marginal means “incremental”. u The marginal utility of commodity i is the rate-of-change of total utility as the quantity of commodity i consumed changes; i. e.
Marginal Utilities u Marginal means “incremental”. u The marginal utility of commodity i is the rate-of-change of total utility as the quantity of commodity i consumed changes; i. e.
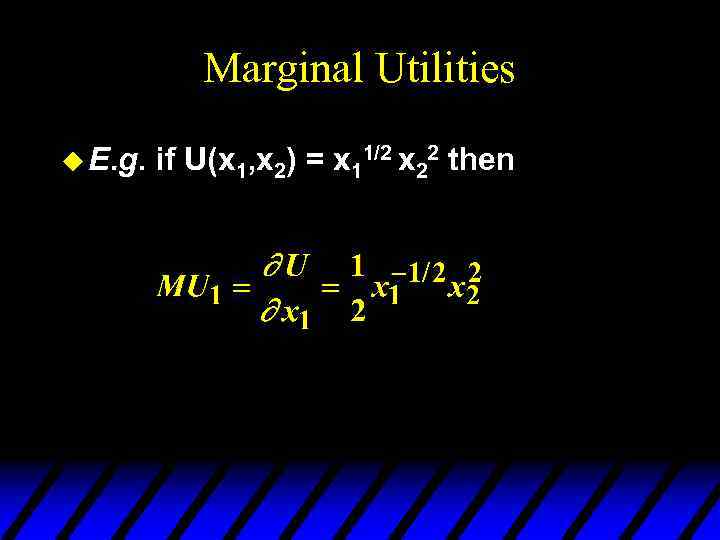 Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
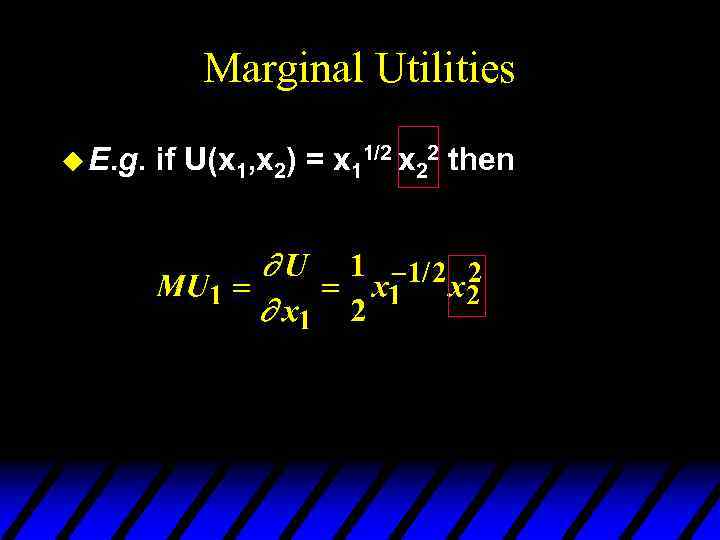 Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
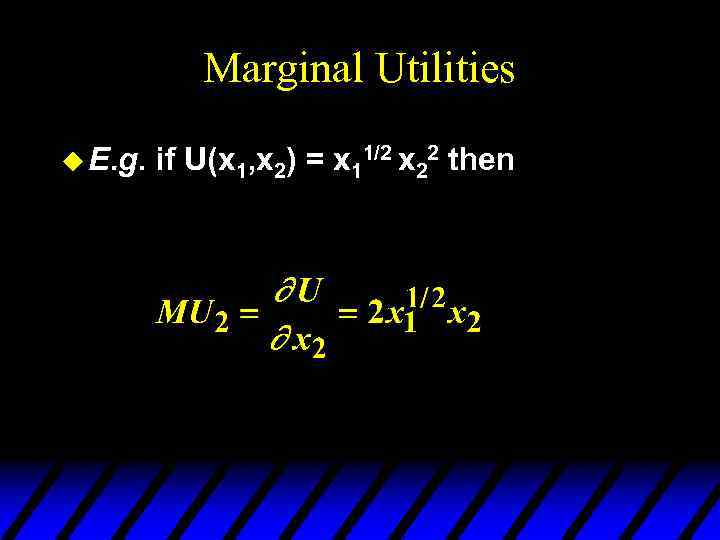 Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
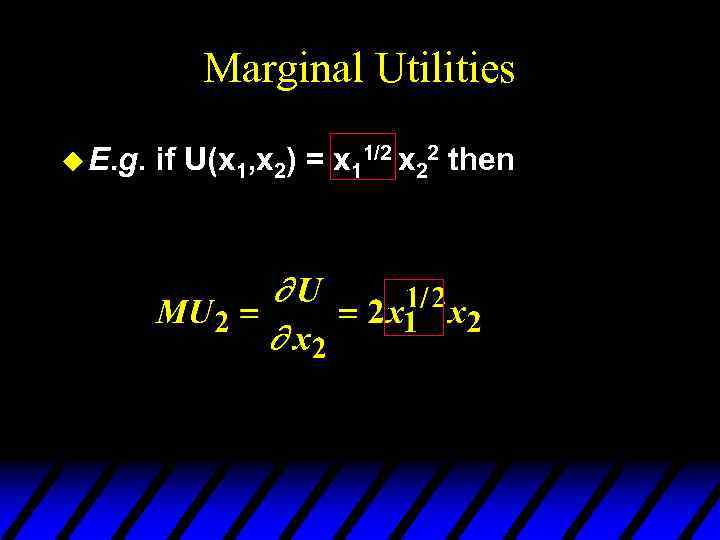 Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
Marginal Utilities u E. g. if U(x 1, x 2) = x 11/2 x 22 then
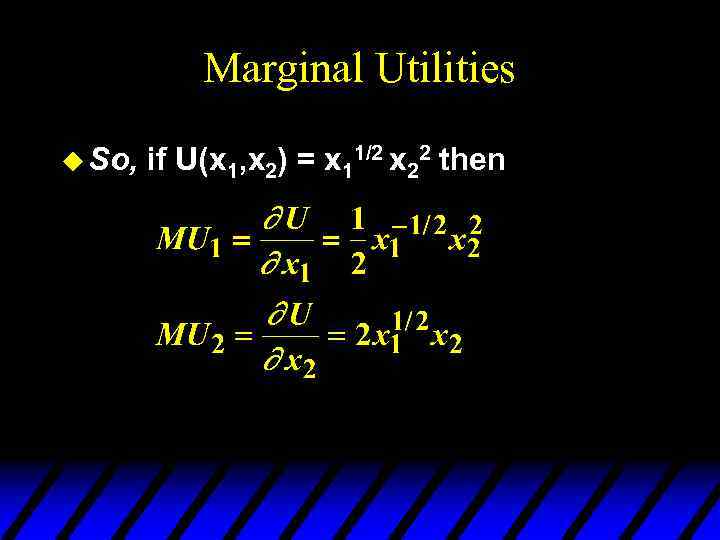 Marginal Utilities u So, if U(x 1, x 2) = x 11/2 x 22 then
Marginal Utilities u So, if U(x 1, x 2) = x 11/2 x 22 then
 Marginal Utilities u Delta U = MU 1 times delta x 1 But the magnitudes of MU depends on magnitude of utility
Marginal Utilities u Delta U = MU 1 times delta x 1 But the magnitudes of MU depends on magnitude of utility
 Marginal Utilities and Marginal Rates-of-Substitution u The general equation for an indifference curve is U(x 1, x 2) k, a constant. Totally differentiating this identity gives
Marginal Utilities and Marginal Rates-of-Substitution u The general equation for an indifference curve is U(x 1, x 2) k, a constant. Totally differentiating this identity gives
 Marginal Utilities and Marginal Rates-of-Substitution rearranged is
Marginal Utilities and Marginal Rates-of-Substitution rearranged is
 Marginal Utilities and Marginal Rates-of-Substitution And rearranged is This is the MRS.
Marginal Utilities and Marginal Rates-of-Substitution And rearranged is This is the MRS.
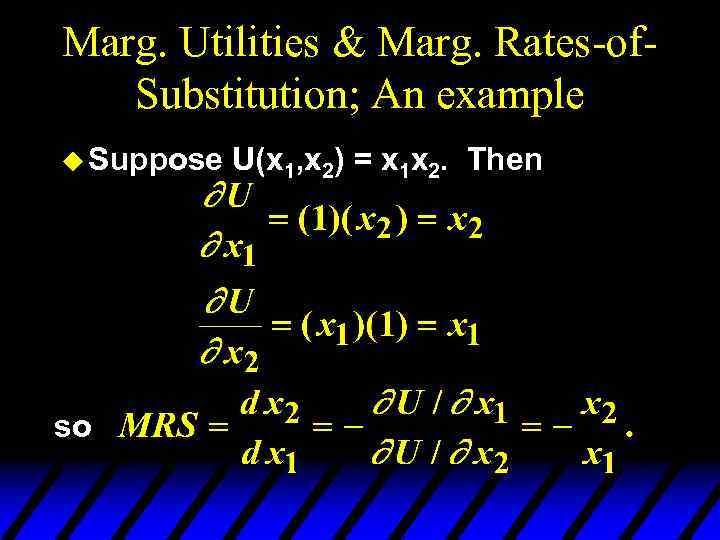 Marg. Utilities & Marg. Rates-of. Substitution; An example u Suppose so U(x 1, x 2) = x 1 x 2. Then
Marg. Utilities & Marg. Rates-of. Substitution; An example u Suppose so U(x 1, x 2) = x 1 x 2. Then
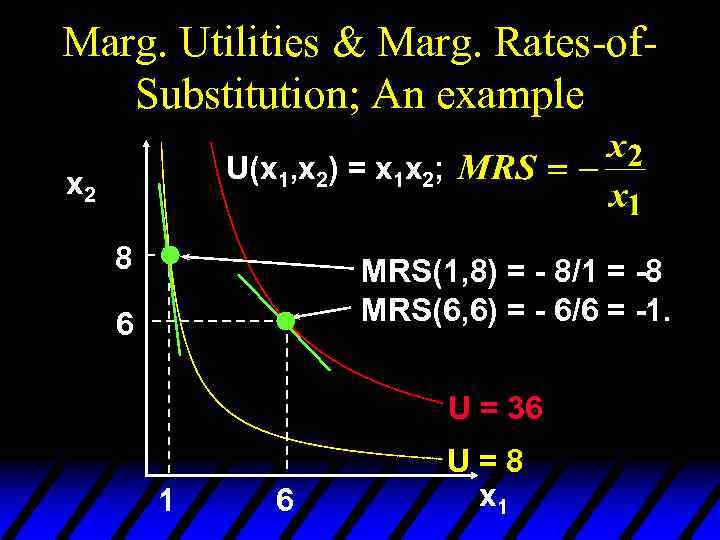 Marg. Utilities & Marg. Rates-of. Substitution; An example U(x 1, x 2) = x 1 x 2; x 2 8 MRS(1, 8) = - 8/1 = -8 MRS(6, 6) = - 6/6 = -1. 6 U = 36 1 6 U=8 x 1
Marg. Utilities & Marg. Rates-of. Substitution; An example U(x 1, x 2) = x 1 x 2; x 2 8 MRS(1, 8) = - 8/1 = -8 MRS(6, 6) = - 6/6 = -1. 6 U = 36 1 6 U=8 x 1
 Marg. Utilities & Marg. Rates-of. Substitution; An example u What happens to MRS if one take a log of Cobb-Douglas utility function? Homework exercies
Marg. Utilities & Marg. Rates-of. Substitution; An example u What happens to MRS if one take a log of Cobb-Douglas utility function? Homework exercies
 Marg. Rates-of-Substitution for Quasi-linear Utility Functions u. A quasi-linear utility function is of the form U(x 1, x 2) = f(x 1) + x 2. so
Marg. Rates-of-Substitution for Quasi-linear Utility Functions u. A quasi-linear utility function is of the form U(x 1, x 2) = f(x 1) + x 2. so
 Marg. Rates-of-Substitution for Quasi-linear Utility Functions = - f (x 1) does not depend upon x 2 so the slope of indifference curves for a quasi-linear utility function is constant along any line for which x 1 is constant. What does that make the indifference map for a quasi-linear utility function look like? u MRS
Marg. Rates-of-Substitution for Quasi-linear Utility Functions = - f (x 1) does not depend upon x 2 so the slope of indifference curves for a quasi-linear utility function is constant along any line for which x 1 is constant. What does that make the indifference map for a quasi-linear utility function look like? u MRS
 x 2 Marg. Rates-of-Substitution for Quasi-linear Utility Functions MRS = - f(x 1’) Each curve is a vertically shifted copy of the others. MRS = -f(x 1”) MRS is a constant along any line for which x 1 is constant. x 1’ x 1” x 1
x 2 Marg. Rates-of-Substitution for Quasi-linear Utility Functions MRS = - f(x 1’) Each curve is a vertically shifted copy of the others. MRS = -f(x 1”) MRS is a constant along any line for which x 1 is constant. x 1’ x 1” x 1
 Monotonic Transformations & Marginal Rates-of-Substitution u Applying a monotonic transformation to a utility function representing a preference relation simply creates another utility function representing the same preference relation. u What happens to marginal rates-ofsubstitution when a monotonic transformation is applied?
Monotonic Transformations & Marginal Rates-of-Substitution u Applying a monotonic transformation to a utility function representing a preference relation simply creates another utility function representing the same preference relation. u What happens to marginal rates-ofsubstitution when a monotonic transformation is applied?
 Monotonic Transformations & Marginal Rates-of-Substitution u For U(x 1, x 2) = x 1 x 2 the MRS = - x 2/x 1. u Create V = U 2; i. e. V(x 1, x 2) = x 12 x 22. What is the MRS for V? which is the same as the MRS for U.
Monotonic Transformations & Marginal Rates-of-Substitution u For U(x 1, x 2) = x 1 x 2 the MRS = - x 2/x 1. u Create V = U 2; i. e. V(x 1, x 2) = x 12 x 22. What is the MRS for V? which is the same as the MRS for U.
 Monotonic Transformations & Marginal Rates-of-Substitution u More generally, if V = f(U) where f is a strictly increasing function, then So MRS is unchanged by a positive monotonic transformation.
Monotonic Transformations & Marginal Rates-of-Substitution u More generally, if V = f(U) where f is a strictly increasing function, then So MRS is unchanged by a positive monotonic transformation.


